近些年来,基于信号循环平稳特性的盲波束形成方法成为了空域抗干扰领域的一个研究热点.循环平稳波束形成算法不需要知道期望信号波形或角度信息,只需根据期望信号的循环频率即可将其从干扰信号和噪声中提取出来[1-4].文献[5]将Cross-SCORE算法引入GPS抗干扰领域,利用卫星信号C/A码的特性,构建一个副波束形成器为主波束形成器提供参考信号,然后求取天线阵列权值系数.但是,当副波束形成器的权矢量求取不准确,也会给主波束带来误差.文献[6]在SCORE算法的基础上提出了一种循环平稳自适应波束形成 (cyclostationary adaptive beamforming,CAB) 方法,但是CAB方法对强干扰信号的抑制能力比较差,并且在采样快拍数目较少时,接收信号阵列协方差矩阵的统计特性受到影响,求取阵列权值的收敛速度较慢[7].为了进一步提高阵列权值的收敛速度,文献[8]提出了对协方差矩阵进行对角加载运算,然后对新的阵列协方差矩阵采用CAB算法进行波束形成.但是该方法中的对角加载因子的选取没有确定的算法,通常以经验值来选取,容易导致波束形成器性能下降[9-12].针对以上算法中的问题,本文提出了基于自适应收缩因子的对角加载方法下循环平稳波束形成器,该方法可以自适应的修正协方差矩阵,收缩因子通过观测矩阵自适应的计算,无需凭借经验值进行人为设定参数, 仿真结果显示本文所提方法与传统循环平稳波束形成算法相比收敛速度较快,并且在低采样快拍数目情况下输出SINR相对较高.
1 阵列信号数学模型考虑M个阵元所组成的阵列天线,假设阵元间各向同性并忽略阵元间互耦作用,阵元间距d为1/2λ,其中λ=c/f,c为光速,f为入射信号的频率.当有一个远场窄带信号入射时,则接收信号模型表示为
| $ \mathit{\boldsymbol{X}}\left( t \right) = \mathit{\boldsymbol{a}}\left( \omega \right)\mathit{\boldsymbol{s}}\left( t \right) + \mathit{\boldsymbol{j}}\left( t \right) + \mathit{\boldsymbol{n}}\left( t \right). $ | (1) |
式中:X(t) 为阵列所接收的M×1维信号; n(t) 为M×1维噪声; j(t) 为M×1维干扰; s(t) 为天线所接收的期望信号; a为信号所对应的M×1维导向矢量阵,可以写成
| $ \mathit{\boldsymbol{a}}\left( \omega \right) = {\left[ {{{\rm{e}}^{j2\pi d\sin \theta /\lambda }} \cdots {{\rm{e}}^{j2\pi \left( {M - 1} \right)d\sin \theta /\lambda }}} \right]^{\rm{T}}}. $ | (2) |
假设期望信号和干扰信号互不相关并且都为平稳信号[13],天线阵列所接收信号的协方差矩阵定义为
| $ \mathit{\boldsymbol{R}} = E\left[ {\mathit{\boldsymbol{X}}\left( t \right){\mathit{\boldsymbol{X}}^{\rm{H}}}\left( t \right)} \right] = \mathit{\boldsymbol{a}}{\mathit{\boldsymbol{R}}_s}{\mathit{\boldsymbol{a}}^{\rm{H}}} + \sigma _n^2\mathit{\boldsymbol{I}}. $ | (3) |
式中:Rs=E[s(t)sH(t)]为期望信号协方差矩阵; (·)H代表矩阵共轭转置; σn2为噪声方差; I为M×M单位矩阵.
在实际中,式 (3) 中的协方差矩阵无法获得.可以根据信号的时间平稳特性,由采样快拍数据得到其最大似然估计值,即
| $ \mathit{\boldsymbol{\hat R = }}\frac{1}{K}\mathit{\boldsymbol{X}}{\mathit{\boldsymbol{X}}^{\rm{H}}} = \frac{1}{K}\sum\limits_{k = 1}^K {\mathit{\boldsymbol{X}}\left( k \right) \cdot {\mathit{\boldsymbol{X}}^{\rm{H}}}\left( k \right)} , $ | (4) |
式中X=[X(1), X(2), …, X(K)]为K个采样快拍组成的数据块.
2 循环波束形成算法近些年,由于信号循环平稳特性的波束形成技术无需期望信号波形或角度辅助,便可在干扰方向形成零陷,同时在期望信号方向形成波束,使其在雷达、声纳和无线通信等领域中得到普遍关注.
2.1 基于SCORE算法的波束形成技术当期望信号具有循环平稳特性,而干扰和噪声在期望信号的循环频率处不具有循环平稳特性时,可以利用SCORE算法来进行波束形成.常用的SCORE波束形成算法有LS-SCORE算法和Cross-SCORE算法[14-15].
阵列天线接收信号模型表示如式 (1) 所示,若期望信号s(t) 在循环频率α处具备频谱自相关特性,而干扰信号和噪声不具备循环频谱特性或在α处不具备频谱自相关特性,则信号X(t) 的循环自相关矩阵表示为
| $ \begin{array}{l} \mathit{\boldsymbol{R}}_{XX}^\alpha \left( \Delta \right) = {\left\langle {\mathit{\boldsymbol{X}}\left( t \right){{\left[ {{\mathit{\boldsymbol{X}}^{\rm{T}}}\left( {t - \Delta } \right){{\rm{e}}^{j2\pi \alpha t}}} \right]}^ * }} \right\rangle _\infty } = \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left\langle {\mathit{\boldsymbol{X}}\left( t \right){\mathit{\boldsymbol{X}}^{\rm{H}}}\left( {t - \Delta } \right){{\rm{e}}^{ - j2\pi \alpha t}}} \right\rangle _\infty } = \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{a}}{\mathit{\boldsymbol{a}}^{\rm{H}}}R_{ss}^\alpha \left( \Delta \right). \hfill \\ \end{array} $ | (5) |
式中:α为循环频率; Δ为延时时间; 〈·〉∞为无限时间平均.
LS-SCORE算法的目标函数为
| $ f\left( \mathit{\boldsymbol{w}} \right) = \mathop {\min }\limits_w {\left\langle {{{\left| {d\left( t \right) - {\mathit{\boldsymbol{w}}^{\rm{H}}}\mathit{\boldsymbol{X}}\left( t \right)} \right|}^2}} \right\rangle _\infty }, $ | (6) |
式中d(t) 为本地参考信号, d(t)=gHX(t-Δ) ej2παt=gHu(t),其中g为本地参考信号的控制向量,u(t)=X(t-Δ) ej2παt.
根据最小均方误差准则,可以求得阵列权值的维纳解为
| $ \mathit{\boldsymbol{w}} = \mathit{\boldsymbol{R}}_{XX}^{ - 1}{\mathit{\boldsymbol{r}}_{Xd}}, $ | (7) |
式中rXd为参考信号d(t) 与输入信号X(t) 之间的的协方差矩阵,可以表示为
| $ {\mathit{\boldsymbol{r}}_{Xd}} = {\left\langle {\mathit{\boldsymbol{X}}\left( t \right){d^{\rm{H}}}\left( t \right)} \right\rangle _\infty } = \mathit{\boldsymbol{R}}_{XX}^\alpha \left( \Delta \right) \cdot \mathit{\boldsymbol{g = a}}{\mathit{\boldsymbol{a}}^{\rm{H}}}\mathit{\boldsymbol{R}}_{ss}^\alpha \left( \Delta \right) \cdot \mathit{\boldsymbol{g}}. $ | (8) |
则阵列权值表示为
| $ \mathit{\boldsymbol{w}} = \mathit{\boldsymbol{R}}_{XX}^{ - 1}\mathit{\boldsymbol{a}}{\mathit{\boldsymbol{a}}^{\rm{H}}}\mathit{R}_{ss}^\alpha \left( \Delta \right) \cdot \mathit{\boldsymbol{g = }}\gamma \mathit{\boldsymbol{R}}_{XX}^{ - 1}\mathit{\boldsymbol{a}}, $ | (9) |
式中γ=Rssα(Δ)aHg为一个标量.
根据以上分析,LS-SCORE算法需要设定控制向量g来求取阵列权值.但是,此控制向量需要根据环境的变化来动态选择,控制向量很容易选取不当,从而导致LS-SCORE波束形成器性能下降.下面所要分析的Cross-SCORE算法是将控制向量g也作为待优化的未知量进行求解,避免控制向量的选取问题.
| $ \left\{ {\mathit{\boldsymbol{w}},\mathit{\boldsymbol{g}}} \right\} = \arg \mathop {\max }\limits_{\mathit{\boldsymbol{w}},\mathit{\boldsymbol{g}}} \frac{{{{\left| {{\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{R}}_{Xu}}\mathit{\boldsymbol{g}}} \right|}^2}}}{{\left( {{\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{R}}_{XX}}\mathit{\boldsymbol{w}}} \right)\left( {{g^{\rm{H}}}{\mathit{\boldsymbol{R}}_{uu}}\mathit{\boldsymbol{g}}} \right)}}. $ | (10) |
| $ \begin{array}{l} {\mathit{\boldsymbol{R}}_{Xu}} = \left\langle {\mathit{\boldsymbol{X}} \cdot {\mathit{\boldsymbol{u}}^{\rm{H}}}} \right\rangle = {\left\langle {\mathit{\boldsymbol{X}}\left( t \right){\mathit{\boldsymbol{X}}^{\rm{H}}}\left( {t - \Delta } \right){{\rm{e}}^{ - j2\pi \alpha t}}} \right\rangle _\infty } = \hfill \\ \;\;\;\;\;\;\;\;\mathit{\boldsymbol{R}}_{XX}^\alpha \left( \Delta \right). \hfill \\ \end{array} $ | (11) |
| $ {\mathit{\boldsymbol{R}}_{uu}} = {\left\langle {\mathit{\boldsymbol{u}} \cdot {\mathit{\boldsymbol{u}}^{\rm{H}}}} \right\rangle _\infty } = {\left\langle {\mathit{\boldsymbol{X}}\left( {t - \Delta } \right){\mathit{\boldsymbol{X}}^{\rm{H}}}\left( {t - \Delta } \right)} \right\rangle _\infty } = {\mathit{\boldsymbol{R}}_{XX}}. $ | (12) |
在每一次采样时刻,矩阵RXu、RXX和Ruu都是常值矩阵,因此式 (10) 可以等价为
| $ \left\{ \begin{array}{l} \mathop {\max }\limits_{\mathit{\boldsymbol{w}},\mathit{\boldsymbol{g}}} {\left| {{\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{R}}_{Xu}}\mathit{\boldsymbol{g}}} \right|^2} = {\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{R}}_{Xu}}\mathit{\boldsymbol{g}}{\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{R}}_{Xu}^{\rm{H}}\mathit{\boldsymbol{w,}} \hfill \\ {\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{R}}_{XX}}\mathit{\boldsymbol{w}} = 1, \hfill \\ {\mathit{\boldsymbol{g}}^{\rm{H}}}{\mathit{\boldsymbol{R}}_{uu}}\mathit{\boldsymbol{g}} = 1. \hfill \\ \end{array} \right. $ | (13) |
对上式应用拉格朗日乘子法,得到
| $ \left\{ \begin{array}{l} \left( {{\mathit{\boldsymbol{R}}_{Xu}}\mathit{\boldsymbol{R}}_{uu}^{ - 1}\mathit{\boldsymbol{R}}_{Xu}^{\rm{H}}} \right)\mathit{\boldsymbol{w = }}\mu {\mathit{\boldsymbol{R}}_{XX}}\mathit{\boldsymbol{w}}, \hfill \\ \left( {\mathit{\boldsymbol{R}}_{Xu}^{\rm{H}}\mathit{\boldsymbol{R}}_{XX}^{ - 1}{\mathit{\boldsymbol{R}}_{Xu}}} \right)\mathit{\boldsymbol{g = }}\mu {\mathit{\boldsymbol{R}}_{uu}}\mathit{\boldsymbol{g}}. \hfill \\ \end{array} \right. $ | (14) |
式中μ为拉格朗日乘子.此时,阵列权值w即等价为矩阵P的主特征向量,矩阵P表示为
| $ \mathit{\boldsymbol{P = R}}_{XX}^{ - 1}\left\{ {{\mathit{\boldsymbol{R}}_{Xu}}\mathit{\boldsymbol{R}}_{uu}^{ - 1}\mathit{\boldsymbol{R}}_{Xu}^{\rm{H}}} \right\}. $ | (15) |
若将RXu和Ruu代入上式得
| $ \mathit{\boldsymbol{P = R}}_{XX}^{ - 1}\left\{ {{\mathit{\boldsymbol{R}}_{Xu}}\mathit{\boldsymbol{R}}_{uu}^{ - 1}\mathit{\boldsymbol{R}}_{Xu}^{\rm{H}}} \right\} = \eta \left\{ {\mathit{\boldsymbol{R}}_{XX}^{ - 1}\mathit{\boldsymbol{a}}{\mathit{\boldsymbol{a}}^{\rm{H}}}} \right\}, $ | (16) |
式中η=|Rssα(Δ)|2aHRXX-1a.式 (16) 表明,矩阵P的主特征向量与RXX-1a成比例,即SCROE波束形成器与最小方差无失真响应 (MVDR) 波束形成器等价.
Cross-SCORE算法是通过最大化阵列输出信号与参考信号之间的谱相关系数来求取阵列权值,但是Cross-SCORE算法求取阵列权矢量和控制向量的过程中,涉及到了广义特征值分解,计算较为复杂.另外,在采样快拍数目较少的情况下,LS-SCORE算法和Cross-SCORE算法的输出SINR较低,且求取阵列权值的收敛速度较慢.
2.2 循环自适性波束形成及其增强算法循环自适应波束形成 (cyclic adaptive beamforming, CAB) 算法是在Cross-SCORE算法的基础上提出的,该算法的目标函数表示为
| $ \left\{ \begin{array}{l} \mathop {\max }\limits_{\mathit{\boldsymbol{w}},\mathit{\boldsymbol{c}}} {\left| {{\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{R}}_{Xu}}\mathit{\boldsymbol{g}}} \right|^2} = \mathop {\max }\limits_{\mathit{\boldsymbol{w}},\mathit{\boldsymbol{c}}} {\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{R}}_{Xu}}\mathit{\boldsymbol{g}}{\mathit{\boldsymbol{g}}^{\rm{H}}}{\mathit{\boldsymbol{R}}_{Xu}}\mathit{\boldsymbol{w}}, \hfill \\ {\mathit{\boldsymbol{w}}^{\rm{H}}}\mathit{\boldsymbol{w}} = 1, \hfill \\ {\mathit{\boldsymbol{g}}^{\rm{H}}}\mathit{\boldsymbol{g}} = 1. \hfill \\ \end{array} \right. $ | (17) |
当干扰信号不具有循环平稳特性或其循环频率与期望信号不相同时,根据上式所求解的阵列权值wCAB与期望信号的导向矢量成比例[10],即
| $ {\mathit{\boldsymbol{w}}_{{\rm{CAB}}}} \propto \mathit{\boldsymbol{a}}\left( \theta \right), $ | (18) |
需要说明的是,当采样快拍数目较少时,上述表达式会受到一定影响.此时的输出信干噪比表示为
| $ {\rm{SINR = }}\frac{{\sigma _s^2{{\left| {\mathit{\boldsymbol{w}}_{{\rm{CAB}}}^{\rm{H}}\mathit{\boldsymbol{a}}\left( \theta \right)} \right|}^2}}}{{\mathit{\boldsymbol{w}}_{{\rm{CAB}}}^{\rm{H}}{\mathit{\boldsymbol{R}}_{j + n}}{\mathit{\boldsymbol{w}}_{{\rm{CAB}}}}}} \approx \frac{{\sigma _s^2{{\left| {\mathit{\boldsymbol{w}}_{{\rm{CAB}}}^{\rm{H}}{\mathit{\boldsymbol{w}}_{{\rm{CAB}}}}} \right|}^2}}}{{\mathit{\boldsymbol{w}}_{{\rm{CAB}}}^{\rm{H}}{\mathit{\boldsymbol{R}}_{j + n}}{\mathit{\boldsymbol{w}}_{{\rm{CAB}}}}}}, $ | (19) |
式中σs2为期望信号的功率,Rj+n为干扰加噪声协方差矩阵.
观察式 (17),该CAB算法没有考虑抑制干扰和噪声,在干扰方向不能形成较深的零陷,导致波束形成器的抗干扰能力不够强.当期望信号导向矢量已知时,可以采用MVDR波束形成器来抑制干扰.根据式 (18) 可知,CAB算法所得到的阵列权值能够近似逼近于期望信号的导向矢量.因此,可以将传统的MVDR波束形成器改写为
| $ \left\{ \begin{array}{l} \mathop {\min }\limits_w {\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{R}}_{XX}}\mathit{\boldsymbol{w}}, \hfill \\ {\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{w}}_{{\rm{CAB}}}} = 1. \hfill \\ \end{array} \right. $ | (20) |
这里将这种算法记为约束循环自适应波束形成 (constrained CAB, CCAB) 算法.根据拉格朗日乘子法,得到CCAB算法的最优权值为
| $ {\mathit{\boldsymbol{w}}_{{\rm{CCAB}}}} = \mathit{\boldsymbol{R}}_{XX}^{ - 1}{\mathit{\boldsymbol{w}}_{{\rm{CAB}}}}. $ | (21) |
该算法与CAB算法类似,在采样快拍数目较少时,接收信号阵列协方差矩阵的统计特性将受到影响,求取的阵列权值收敛速度较慢.此时,可以采用对角加载方法来对阵列协方差矩阵进行校正,得到一种基于对角加载的循环自适应波束形成 (diagonal loading CAB, DL-CAB) 算法,即
| $ {\mathit{\boldsymbol{w}}_{{\rm{DL}} - {\rm{CAB}}}} = {\left( {{\mathit{\boldsymbol{R}}_{XX}} + \varepsilon \mathit{\boldsymbol{I}}} \right)^{ - 1}}{\mathit{\boldsymbol{w}}_{{\rm{CAB}}}}. $ | (22) |
上述ε为对角加载因子.该方法能够在小快拍数目的情况下保证波束形成器的稳健性,但是ε值的选取没有确定的算法,通常以经验值来选取,容易导致波束形成器性能下降[16-17].
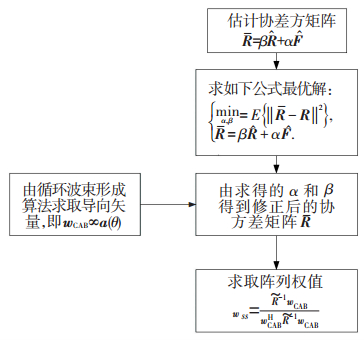
3 改进的循环波束形成算法上面介绍的循环平稳收缩算法环平稳波束形成算法,都是通过选定特定的对角加载因子量,收敛速度和算法的性能都与加载因子的选取有关,本章节并针对循环平稳波束形成器收敛速度慢的问题,提出了一种基于收缩方法的稳健循环平稳波束形成器,该方法的收缩因子随着快拍数自适应变化,仿真验证了所提方法相比于传统方法的优势. 图 1为改进的循环波束形成算法的流程.
|
图 1 改进波束形成算法流程 Figure 1 The diagram of beamforming algorithm |
采样快拍数目很大时,采样协方差矩阵
现将估计的阵列协方差矩阵表示为
| $ \mathit{\boldsymbol{\tilde R = }}\beta \mathit{\boldsymbol{\hat R + }}\alpha \mathit{\boldsymbol{\hat F}}. $ | (23) |
式中:α、β为收缩因子,且需满足α > 0,β > 0;α/β为收缩因子比值;
现需要选择合适的收缩系数α、β,使
| $ \left\{ \begin{array}{l} \mathop {\min }\limits_{\alpha ,\beta } = E\left\{ {{{\left\| {\mathit{\boldsymbol{\tilde R}} - \mathit{\boldsymbol{R}}} \right\|}^2}} \right\}, \hfill \\ \mathit{\boldsymbol{\tilde R}} = \beta \mathit{\boldsymbol{\hat R + }}\alpha \mathit{\boldsymbol{\hat F}}. \hfill \\ \end{array} \right. $ | (24) |
上式进行展开为
| $ \begin{array}{l} {\rm{MSE}}\left( {\mathit{\boldsymbol{\tilde R}}} \right) = E\left\{ {{{\left\| {\mathit{\boldsymbol{\tilde R}} - \mathit{\boldsymbol{R}}} \right\|}^2}} \right\} = \hfill \\ \;\;\;\;E\left\{ {{{\left\| {\alpha \mathit{\boldsymbol{\hat F}} - \left( {1 - \beta } \right)\mathit{\boldsymbol{R + }}\beta \left( {\mathit{\boldsymbol{\hat R}} - \mathit{\boldsymbol{R}}} \right)} \right\|}^2}} \right\} = \hfill \\ \;\;\;\;{\alpha ^2}{\left\| {\mathit{\boldsymbol{\hat F}}} \right\|^2} - 2\alpha \left( {1 - \beta } \right){\rm{tr}}\left( {{{\mathit{\boldsymbol{\hat F}}}^ * } \cdot \mathit{\boldsymbol{R}}} \right) + \hfill \\ \;\;\;\;{\left( {1 - \beta } \right)^2}{\left\| \mathit{\boldsymbol{R}} \right\|^2} + {\beta ^2}E\left\{ {{{\left\| {\mathit{\boldsymbol{\hat R}} - \mathit{\boldsymbol{R}}} \right\|}^2}} \right\}. \hfill \\ \end{array} $ | (25) |
式中‖·‖为Frobenius范数,即
| $ \alpha = \frac{{\left( {1 - \beta } \right){\rm{tr}}\left( {{{\mathit{\boldsymbol{\hat F}}}^ * } \cdot \mathit{\boldsymbol{R}}} \right)}}{{{{\left\| {\mathit{\boldsymbol{\hat F}}} \right\|}^2}}}. $ | (26) |
将式 (26) 代入式 (25),得
| $ \begin{array}{l} {\rm{MSE}}\left( {\mathit{\boldsymbol{\tilde R}}} \right) = \frac{{{{\left( {1 - \beta } \right)}^2}\left[ {{{\left\| {\mathit{\boldsymbol{\hat F}}} \right\|}^2} \cdot {{\left\| \mathit{\boldsymbol{R}} \right\|}^2} - {{\left( {{\rm{tr}}\left( {{{\mathit{\boldsymbol{\hat F}}}^ * } \cdot \mathit{\boldsymbol{R}}} \right)} \right)}^2}} \right]}}{{{{\left\| {\mathit{\boldsymbol{\hat F}}} \right\|}^2}}} + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\beta ^2}E\left\{ {{{\left\| {\mathit{\boldsymbol{\hat R}} - \mathit{\boldsymbol{R}}} \right\|}^2}} \right\}. \hfill \\ \end{array} $ | (27) |
再令
| $ \beta = \frac{\gamma }{{\eta + \gamma }}. $ | (28) |
式中
| $ \eta = E\left\{ {{{\left\| {\mathit{\boldsymbol{\hat R}} - \mathit{\boldsymbol{R}}} \right\|}^2}} \right\}, $ | (29) |
| $ \gamma = \frac{{{{\left\| {\mathit{\boldsymbol{\hat F}}} \right\|}^2} \cdot {{\left\| \mathit{\boldsymbol{R}} \right\|}^2} - {{\left( {{\rm{tr}}\left( {{{\mathit{\boldsymbol{\hat F}}}^ * } \cdot \mathit{\boldsymbol{R}}} \right)} \right)}^2}}}{{{{\left\| {\mathit{\boldsymbol{\hat F}}} \right\|}^2}}}. $ | (30) |
由Cauchy-Schwartz不等式,知γ > 0.根据式 (28),知β∈(0, 1).此外,由
下面进一步对γ进行化简,令
| $ \begin{array}{l} \gamma = {\left\| \mathit{\boldsymbol{R}} \right\|^2} - 2\frac{{{{\left( {{\rm{tr}}\left( {{{\mathit{\boldsymbol{\hat F}}}^ * } \cdot \mathit{\boldsymbol{R}}} \right)} \right)}^2}}}{{{{\left\| {\mathit{\boldsymbol{\hat F}}} \right\|}^2}}} + \frac{{{{\left( {{\rm{tr}}\left( {{{\mathit{\boldsymbol{\hat F}}}^ * } \cdot \mathit{\boldsymbol{R}}} \right)} \right)}^2}}}{{{{\left\| {\mathit{\boldsymbol{\hat F}}} \right\|}^2}}} = \hfill \\ \;\;\;\;\;\;\left\| {\xi \mathit{\boldsymbol{\hat F}} - \mathit{\boldsymbol{R}}} \right\|. \hfill \\ \end{array} $ | (31) |
将真实的阵列协方差矩阵R用采样协方差矩阵代替,则收缩因子α和β的估计值分别写为
| $ \hat \alpha - \hat \zeta \left( {1 - \hat \beta } \right), $ | (32) |
| $ \hat \beta = \frac{{\hat \gamma }}{{\hat \eta + \hat \gamma }}. $ | (33) |
式中
根据上节所介绍的方法求得收缩因子
| $ \left\{ \begin{array}{l} \mathop {\min }\limits_{{\mathit{\boldsymbol{w}}_{ss}}} \mathit{\boldsymbol{w}}_{ss}^{\rm{H}}\mathit{\boldsymbol{\tilde R}}{\mathit{\boldsymbol{w}}_{ss}}, \hfill \\ \mathit{\boldsymbol{w}}_{ss}^{\rm{H}}{\mathit{\boldsymbol{w}}_{{\rm{CAB}}}} = 1. \hfill \\ \end{array} \right. $ | (34) |
这里将上述波束形成方法简记为收缩CAB方法,其阵列权值wss为
| $ {\mathit{\boldsymbol{w}}_{ss}} = \frac{{{{\mathit{\boldsymbol{\tilde R}}}^{ - 1}}{\mathit{\boldsymbol{w}}_{{\rm{CAB}}}}}}{{\mathit{\boldsymbol{w}}_{{\rm{CAB}}}^{\rm{H}}{{\mathit{\boldsymbol{\tilde R}}}^{ - 1}}{\mathit{\boldsymbol{w}}_{{\rm{CAB}}}}}} = \frac{{{{\left( {\hat \beta \mathit{\boldsymbol{\hat R + }}\hat \alpha \mathit{\boldsymbol{\hat F}}} \right)}^{ - 1}}{\mathit{\boldsymbol{w}}_{{\rm{CAB}}}}}}{{\mathit{\boldsymbol{w}}_{{\rm{CAB}}}^{\rm{H}}{{\left( {\hat \beta \mathit{\boldsymbol{\hat R + }}\hat \alpha \mathit{\boldsymbol{\hat F}}} \right)}^{ - 1}}{\mathit{\boldsymbol{w}}_{{\rm{CAB}}}}}}. $ | (35) |
对应的输出信干噪比为
| $ {\rm{SINR = }}\frac{{\sigma _s^2{{\left| {\mathit{\boldsymbol{w}}_{ss}^{\rm{H}}{\mathit{\boldsymbol{w}}_{{\rm{CAB}}}}} \right|}^2}}}{{\mathit{\boldsymbol{w}}_{ss}^{\rm{H}}\left( {\hat \beta \mathit{\boldsymbol{\hat R + }}\hat \alpha \mathit{\boldsymbol{\hat F}}} \right){\mathit{\boldsymbol{w}}_{ss}}}}. $ | (36) |
从式 (35) 可以看出,收缩CAB方法是在CAB算法的基础上,采用自适应收缩因子形式的对角加载方法来求取阵列权值.
4 仿真实验与分析采用10阵元均匀线阵,阵元间距为卫星信号的半波长.假设卫星信号来向为0°,信噪比为-20 dB.卫星信号中频频率设定为f0=4.130 4 MHz,采样频率为fs=16.368 MHz,C/A码频率为fC/A=1.023 MHz,这里取卫星信号的循环频率2f0+fC/A. 3个窄带干扰信号的来向分别假设为30°、-40°、50°.各阵元的通道噪声假设为不相关的高斯白噪声.下面两个实验均采用100次Monte-Carlo仿真.
实验1 低功率干扰下的波束形成器性能分析.卫星信号本身具有30 dB的扩频增益,因此当干信比大于30 dB,接收机跟踪环路将无法正常工作.在实验1中,3个干扰信号的干噪比分别假设为10、15、20 dB,对应的干信比分别为30、35、40 dB,干扰功率相对卫星信号的扩频增益不算很大.
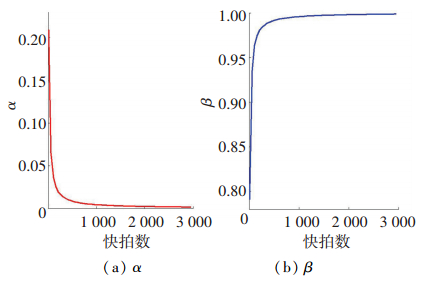
图 2给出了所提方法收缩因子α、β随着采样快拍数目的变化曲线.从图中可以看出,收缩因子α、β均位于 (0, 1).当快拍数目为500左右时,收缩因子α、β不再发生明显变化, 即随着采样快拍数目的增加,收缩因子α值趋近与0,收缩因子β值趋近于1.
|
图 2 收缩因子随着快拍数目的变化 Figure 2 Shrinkage parameters versus the number of snapshots |
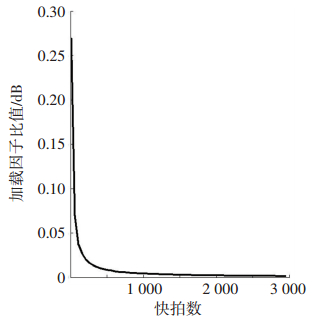
图 3给出了收缩因子比值随着快拍数目变化,收缩因子比值与收缩因子α的变化趋势一致,而与收缩因子β的变化趋势相反,并且当快拍数目为500左右时趋于稳定.
|
图 3 收缩因子比值随着快拍数目的变化 Figure 3 Shrinkage parameters ratio versus the number of snapshots |
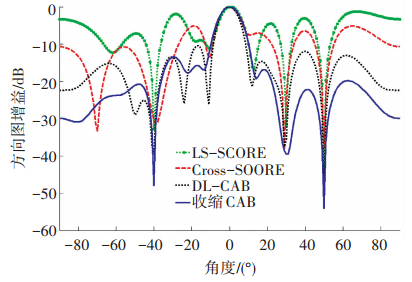
为了比较所提方法与前文所述方法的性能,图 4给出了LS-SCORE、Cross-SCORE、DL-CAB和收缩CAB方法在采样快拍数为1 000时的方向图增益.在LS-SCORE波束形成算法中,控制向量g取M×1维向量g=[1 0 … 0]T.在DL-CAB波束形成算法中,对角加载量取ε=tr[σs2a(θ0)aH(θ0)], σs2和a(θ0) 分别为卫星信号的功率和导向矢量.从图 4中可以看出,上述两种方法均能够在干扰方向30°、-40°、50°处形成零陷且能够在卫星信号方向形成波束.另外,干扰功率越大的信号,其对应方向处的零陷深度越深.但是LS-SCORE和Cross-SCORE算法的波束旁瓣比较高,将影响波束形成器的输出SINR.
|
图 4 采样快拍数为1 000时的波束方向图 Figure 4 Beanpattern for snapshot number equal to 1 000 |
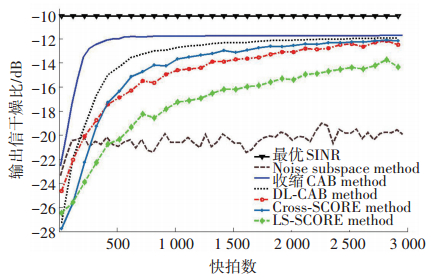
图 5给出了最优SINR、噪声子空间 (Noise subspace)、LS-SCORE、Cross-SCORE、CCAB、DL-CAB和收缩CAB方法在不同采样快拍数目时的输出SINR.由于信噪比为-20 dB且阵元数目M=10,此时理想的最优SINR为10lg (M·RSN)=-10 dB.噪声子空间零陷形成方法只能在干扰处形成零陷,而不能在卫星信号处形成波束.因此,在采样快拍数目达到200后,其输出SINR近似等于输入信号的信噪比.从图中还可看出,LS-SCORE、Cross-SCORE、CCAB、DL-CAB和收缩CAB方法的输出SINR均能够随着采样快拍数目的增加而增大.但是LS-SCORE算法的收敛速度很慢,当采样快拍数目达到3 000时,其输出SINR只能达到-14 dB左右.与LS-SCORE算法相比,Cross-SCORE和CCAB算法的收敛速度较快.当采样快拍数目达到3 000时,这两种方法的输出SINR能达到-12 dB左右.但是这两种方法在低采样快拍数目下,输出SINR均不高.当在采样快拍数目达到500时,它们的输出SINR不足-16 dB.另外,在采样快拍数目低于400时,Cross-SCORE算法的输出SINR低于CCAB方法所对应的值.由于DL-CAB和收缩CAB方法均采用了加载信息量,与其他算法相比收敛速度更快. DL-CAB在采样快拍数目达到1 500时,其输出SINR接近-12 dB,而收缩CAB方法在采样快拍数目为500左右时,其输出SINR就已经达到-12 dB.在采样快拍数目低于500时,收缩CAB方法的输出SINR明显比其他算法要高.
|
图 5 输出信干噪比随着采样快拍数目的变化曲线 Figure 5 Output SINR versus the number of snapshots |
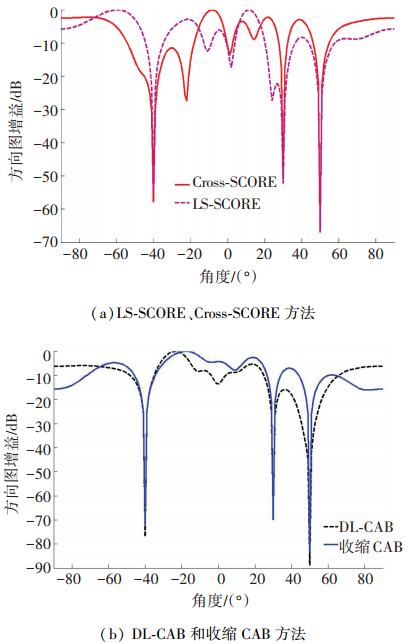
实验2 高功率干扰下的波束形成器性能分析.在实验2中,3个干扰信号的干噪比分别设定为30、40、50 dB,对应的干信比分别为50、60、70 dB,干扰功率远大于卫星信号自身的扩频增益,此处认为这些干扰信号为强干扰. LS-SCORE波束形成算法中的控制向量g和DL-CAB波束形成算法中的对角加载量ε均与实验一中的参数相同. 图 6(a)、6(b)分别给出了LS-SCORE、Cross-SCORE方法和DL-CAB、收缩CAB方法在采样快拍数为1 000时的方向图增益. DL-CAB和收缩CAB方法在干扰处所形成的零陷深度要大于LS-SCORE和Cross-SCORE方法.
|
图 6 采样快拍数为1 000时的波束方向图 Figure 6 Beampattern for snapshot number equal to 1 000 |
但由于3个干扰信号的功率过强,单独依靠卫星信号的循环频率,采用频谱自相关重构 (SCORE) 类算法很难将卫星信号从干扰和噪声中提取出来.从图 6(a)中可以看出LS-SCORE和Cross-SCORE不能在卫星信号方向形成波束.而DL-CAB和收缩CAB方法是在CAB方法的基础上改进的,CAB方法属于SCORE算法的一种特殊情况.从图 6(b)中可以看出,这两种改进的方法在干扰功率很高的情况下,也不能在卫星信号方向形成波束.
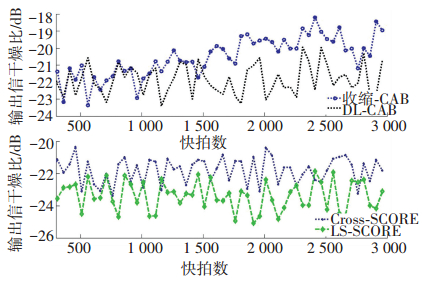
为了比较上述LS-SCORE、Cross-SCORE、DL-CAB和收缩CAB方法在高功率干扰情况下的输出SINR,图 7给出了这4种方法在不同采样快拍数目下的输出SINR.从图中可以看出,当采样快拍数目达到300时,LS-SCORE算法的输出SINR基本上稳定在-23 dB,Cross-SCORE和DL-CAB算法的输出SINR在-22 dB上下波动.采样快拍数目在300~1 000之间时,收缩CAB方法的输出SINR基本上也维持在-22 dB左右.当采样快拍数目大于1 000时,收缩CAB方法的输出SINR缓慢波动增加.在采样快拍数目达到3 000时,其输出SINR为-19 dB.观察这四种方法的输出SINR,它们与噪声子空间方法的输出SINR值接近,这与它们的波束方向图也类似而吻合.
|
图 7 输出信干噪比随着采样快拍数目的变化曲线 Figure 7 Output SINR versus the number of snapshots |
1) 当干扰功率较低且采样快拍数足够大时,LS-SCORE、Cross-SCORE、CCAB、DL-CAB和收缩CAB方法均能够在干扰方向形成零陷、在卫星信号方向形成波束.与其他算法相比,所提出的收缩CAB算法的输出SINR相对较高,且收敛速度更快.
2) 在高功率干扰信号下,LS-SCORE、Cross-SCORE、CCAB、DL-CAB和收缩CAB算法均只能够在干扰方向形成零陷,不能在卫星信号方向形成波束,但是所提出的收缩CAB算法的输出SINR仍略高于其他算法.
| [1] | NAPOLITANO A. Cyclostationarity: new trends and applications[J]. Signal Processing, 2016, 120(384): 385-480. DOI: 10.1016/j.sigpro.2015.09.011 |
| [2] | LEE J H, HUANG C C. Adaptive cyclostationary array beamforming with robust capabilities[J]. Journal of the Franklin Institute, 2015, 352(6): 2486-2503. DOI: 10.1016/j.jfranklin.2015.03.029 |
| [3] |
杨莘元, 陈四根, 郝敬涛. 一种稳健的自适应波束形成方法[J].
哈尔滨工业大学学报, 2005, 37(10): 132-135.
YANG Shenyuan, CHEN Sigen, HAO Jingtao. Robust capon beamforming in high frequency surface wave radar[J]. Journal of Harbin Institute of technology, 2005, 37(10): 132-135. |
| [4] | ARJUNA M, NILAN U. Directional cyclostationary feature detectors using 2-D IIR RF spiral-antenna beam digital filters[C]//2014 IEEE International Symposium on Circuits and Systems. Melbourne: IEEE Press, 2014:2499-2502. DOI: 10.1109/ISCAS.2014.6865680. |
| [5] | AMIN M G, SUN W. A novel interference suppression scheme for global navigation satellite systems using antenna array[J]. IEEE Journal on Selected Areas in Communications, 2005, 23(5): 999-1012. DOI: 10.1109/JSAC.2005.845404 |
| [6] | NAI S E, SER W, YU Z L, et al. Iterative robust minimum variance beamforming[J]. IEEE Transactions on Signal Processing, 2011, 59(4): 1601-1611. DOI: 10.1109/tsp.2010.2096222 |
| [7] | WANG Yasen, BAO Qinglong, CHEN Zengping. Robust adaptive beamforming using IAA-based interference-plus-noise covariance matrix reconstruction[J]. Electronics Letters, 2015, 52(13): 1185-1186. DOI: 10.1049/el.2015.4420 |
| [8] | CARLSON B D. Covariance matrix estimation errors and diagonal loading in adaptive arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 1988, 24(7): 397-401. DOI: 10.1109/7.7181 |
| [9] | HANG Ruan, LAMARE D, RODRIGO C. Low-complexity robust adaptive beamforming algorithms exploiting shrinkage for mismatch estimation[J]. IET Signal Processing, 2016, 10(5): 429-438. DOI: 10.1049/iet-spr.2014.0331 |
| [10] | ZHAO Haijun, ZHANG Jing, YIN Zhiping. Adaptive beamforming based on stochastic parallel gradient descent algorithm for single receiver phased array[C]// The 2014 International Conference on Systems and Informatics.Shanghai:IEEE Press, 2015: 849-853. DOI: 10.1109/ICSAI.2014.7009403. |
| [11] | GOU X M, LIU Z W, XU Y G. Fully automatic robust adaptive beamforming using the constant modulus feature[J]. IET Signal Processing, 2014, 8(8): 823-830. DOI: 10.1049/iet-spr.2013.0416 |
| [12] | ZHUANG J, MANIKAS A. Interference cancellation beamforming robust to pointing errors[J]. IET Signal Processing, 2013, 7(2): 120-127. DOI: 10.1049/iet-spr.2011.0464 |
| [13] | CHOI Y H. Subspace based adaptive beamforming method with low complexity[J]. Electronics Letters, 2011, 47(9): 529-530. DOI: 10.1049/el.2011.0512 |
| [14] | LEE J H, HUANG C C. Blind adaptive beamforming for cyclostationary signals: a subspace projection approach[J]. IEEE Antennas and Wireless Propagation Letters, 2009, 8: 1406-1409. DOI: 10.1109/LAWP.2010.2040364 |
| [15] | VOROBYOV S A, GERSHMAN A B, LUO Z Q. Robust adaptive beamforming using worst-case performance optimization:a solution to the signal mismatch problem[J]. IEEE Transactions on Signal Processing, 2003, 51(2): 313-324. DOI: 10.1109/tsp.2002.806865 |
| [16] |
焦圣喜, 王睿, 李婉珍. 自适应波束形成算法[J].
信息与控制, 2015, 44(2): 165-170.
JIAO Shengxi, WANG Rui, LI Wanzhen. Adaptive beamforming algorithms[J]. Information and Control, 2015, 44(2): 165-170. DOI: 10.13976/j.cnki.xk.2015.0165 |
| [17] | ZHANG Yuping, LI Yunjie, GAO Meiguo. Robust adaptive beamforming based on the effectiveness of reconstruction[J]. Signal Processing, 2016, 120: 572-579. DOI: 10.1016/j.sigpro.2015.09.039 |
 2017, Vol. 49
2017, Vol. 49


