桥梁综合评估是通过各种可行的人工检查和长期监测手段,获得可以反映桥梁结构技术状态的参数信息,并在此基础上运用相关理论对获得的信息进行综合分析,最终对桥梁的病害情况、损伤程度、承载能力等方面作出评价[1].中国目前针对公路桥梁使用的评估类规范标准[2-3]主要面向中小跨径桥梁,对于大跨径斜拉桥的评估,其在指标体系和评定标准方面存在一定局限.同时,评定标准中采用的是分层综合评定与单项指标控制相结合的方法,该方法概念清晰,计算简单,被广泛应用.然而层次分析法无法解决各类评估信息表现出的模糊、不完全等特性,因此,有学者提出基于模糊理论的评估方法[4]用于解决该问题.但是,在实际评估过程中,当出现子指标之间评定差异较大的状况时,模糊理论亦无法解决.证据理论[5-7]技术为桥梁综合评估提供了新思路,底层证据的基本可信度考虑了指标的模糊性,同时通过某种合成规则将多个证据进行合成,从而得到具有更高可信度的评估结果.证据理论技术已经发展了40余年,在诸多领域得到了广泛研究和应用,如工业过程监视、环境监视、复杂系统的状态监测与诊断维护等[8-10].在桥梁的综合技术状况评价领域,已有学者在基于信息融合的结构损伤识别[11-12]、桥面板的评定[13]以及基于证据推理的桥梁状态评估[14-15]等开展了一系列的研究工作,而对于斜拉桥这类大型、复杂结构的桥梁的综合评估,目前的研究尚不多见.为此,本文在已有研究成果的基础上,以一座钢结构斜拉桥为研究对象,结合了长期监测数据和人工检查信息,建立了基于证据理论的桥梁综合评估模型,并通过实桥计算进行验证分析.
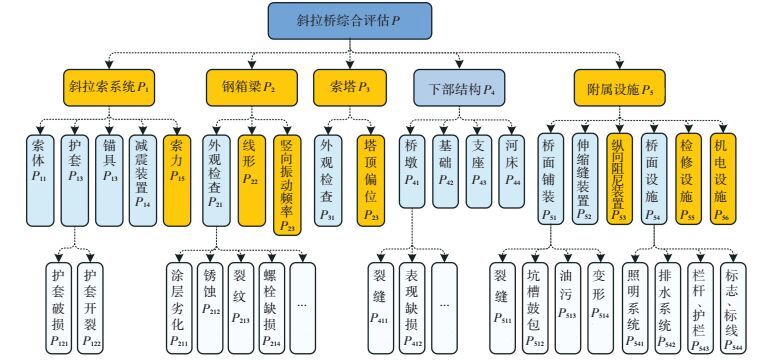
1 评估指标的来源现有评定标准中指标绝大部分为外观检查信息,结合一些无损检测数据.这种检查方式侧重于外观损伤,直观简捷,但是存在检查盲点、评判主观等问题;长期监测系统近年来在大跨径桥梁上应用较为广泛,监测数据也可对桥梁状况作出评价.对于本文的研究对象,传感器数量达600个,监测种类众多,包括索力、主梁挠度、振动特性、温度、应力等.然而运营至今,传感器出现了不同程度的损坏或失真,以索力为例,截至目前,故障率已达67.3%,这无疑影响了评估的准确性.因此,两类评估源均存在一定利弊.本文考虑将两者融合,以进一步提高评估结果的可靠性.首先需根据规范制定新的指标体系.在评定标准的指标体系中,目标层下面的第1层分为上部结构、下部结构以及桥面系,这种划分方式更适宜中小跨径梁桥,针对大跨径斜拉桥的结构特点,结合检测的常用分类方法,将其分为钢箱梁、斜拉索系统、索塔、下部结构以及附属设施.第2层包括17个部件,但是仍未能涵盖斜拉桥的所有部件,例如纵向阻尼装置、除湿系统、检修系统等,本文增加部分斜拉桥特有部件以及长期监测数据,建立一套斜拉桥综合评估指标体系,如图 1所示.该指标体系的目标层为斜拉桥综合技术状况,指标体系在目标层下面设置了3层,第1层为斜拉桥5大部件;第2层为更细化的部件;第3层为具体病害指标.由于涉及的病害项较多,出于篇幅考虑,在此仅列出部分关键的病害层指标.图中指标以Pi、Pij、Pijk作标记,其中i为第1层中第i个指标的编号,j为第2层中第j个指标的标号,k为第3层中第k个指标的编号.
|
图 1 斜拉桥综合评估指标体系 Figure 1 Comprehensive evaluation index system of cable-stayed bridge |
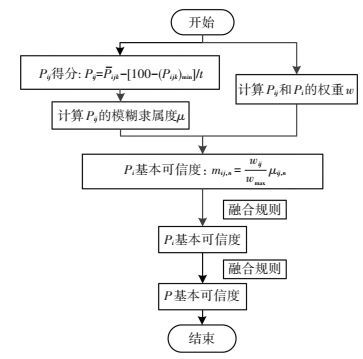
斜拉桥融合评估算法计算流程如图 2所示.从图中可以看出,计算可分3步进行,具体步骤如下:1) 参照评定标准中的构件扣分相关公式计算第2层指标的部件得分,并计算各自隶属度.2) 利用层次分析法计算层次体系中第1层和第2层指标的权重.结合模糊隶属度和权重的计算结果,计算第2层指标的基本可信度.3) 根据融合规则,计算第1层指标的可信度以及顶层斜拉桥的总体评估结果.下面对每个步骤进行分述.
|
图 2 基于证据理论的评估流程 Figure 2 Flow chart of the assessment based on the evidence theory |
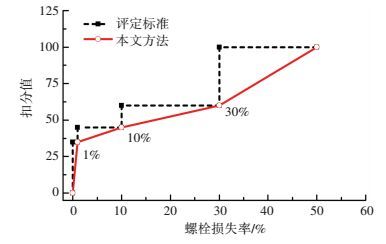
评定标准中对于构件的评定等级规定:根据不同构件病害对桥梁影响程度,对病害划分为不同级数,并采用分级扣分的方式.该方法虽已考虑了不同类型病害的权重,但扣分值起点似过高且呈梯度上升.例如,桥墩出现0.1%或者15%的蜂窝、麻面,对应评定标准均是扣20分,这样的扣分方式过于严格,而且对于结构病害的长期观测趋势反映不明显.鉴于此,本文提出一种分段线性上升的指标评定标准,以明确病害程度与扣分值之间一一对应的定量关系.以钢箱梁高强螺栓缺损这一病害指标为例,图 3给出了既有标准和本文方法的评定标准.
|
图 3 螺栓缺损的评定标准 Figure 3 Evaluation criteria of the bolt defect |
从图中可以看出,本文提出的分段线性扣分方式能够更客观地反映不同程度病害的扣分值,尤其是在第一段 (螺栓损失率≤1%),构件扣分值不再是统一的35分,而是从0到35分线性变化,使得扣分值具有更好的针对性及合理性.
每个病害指标可依照该方法建立起多段线性扣分模式.另外,对于指标体系中新增的部分长期监测数据,例如索力、主梁振动频率、挠度等,可通过线形适度模型[14]进行专项评定.
2.2 指标权重由于指标体系的变更,因此需要通过问卷调查确定各指标的权重w.面向桥梁设计、养护、科研等单位,调研42位专家,通过层次分析法确定,篇幅有限,在此不再赘述.由此得到第1层指标的权重值分别为0.24,0.21,0.2,0.28和0.07,斜拉索系统下的第2级指标权重值分别为0.38,0.1,0.24,0.08和0.2,钢箱梁下的第2级指标权重值分别为0.63,0.27和0.1,索塔下的第2级指标权重值分别为0.4和0.6,下部结构下的第2级指标权重值分别为0.35,0.4,0.15和0.1,附属设施下的第2级指标权重值分别为0.35,0.2,0.15,0.2,0.05和0.05.
2.3 基本可信度在指标体系中,第2层指标的初始基本可信度由模糊隶属度函数方法赋值,因此首先需要选定底层指标的隶属度函数.
在评定标准中将斜拉桥综合状态分为1~5级.为与此分类相适应,斜拉桥综合状态评估的评语集合表示为E={e1, e2, e3, e4, e5}, 它们分别对应1类、2类、3类、4类及5类.以Pij指标为例,其隶属度可表示为
| $ S\left( {{P_{ij}}} \right) = \left\{ {{\mu _{ij,n}}\left| {n = 1,2,3,4,5} \right.} \right\}. $ |
式中μij, n为指标Pij相对于评估等级en的模糊函数值.
隶属度函数的形式有很多,以往学者多采用三角形或梯形,而实际上,隶属度的变化符合非线性的特点,因此选择岭型分布函数更合适[16].在实际工程应用中,岭型分布也分为3种:升岭型分布、降岭型分布以及中间型岭型分布.以指标P11为例,其各级隶属度计算公式分别为
| $ {\mu _{11,1}} = \left\{ {\begin{array}{*{20}{c}} {\frac{1}{2} + \frac{1}{2}\sin \left[ {\frac{\pi }{{7.5}}\left( {x - 93.8} \right)} \right],}&{x \in \left[ {90,97.5} \right);} \\ {1,}&{x \in \left[ {97.5,100} \right].} \end{array}} \right. $ |
| $ {\mu _{11,2}} = \left\{ {\begin{array}{*{20}{c}} {\frac{1}{2} + \frac{1}{2}\sin \left[ {\frac{\pi }{{10}}\left( {x - 80} \right)} \right],}&{x \in \left[ {75,85} \right);} \\ {1,}&{x \in \left[ {85,90} \right);} \\ {\frac{1}{2} - \frac{1}{2}\sin \left[ {\frac{\pi }{{7.5}}\left( {x - 93.8} \right)} \right],}&{x \in \left[ {90,97.5} \right].} \end{array}} \right. $ |
| $ {\mu _{11,3}} = \left\{ {\begin{array}{*{20}{c}} {\frac{1}{2} + \frac{1}{2}\sin \left[ {\frac{\pi }{{10}}\left( {x - 60} \right)} \right],}&{x \in \left[ {55,65} \right);} \\ {1,}&{x \in \left[ {65,75} \right);} \\ {\frac{1}{2} - \frac{1}{2}\sin \left[ {\frac{\pi }{{10}}\left( {x - 80} \right)} \right],}&{x \in \left[ {75,85} \right].} \end{array}} \right. $ |
| $ {\mu _{11,4}} = \left\{ {\begin{array}{*{20}{c}} {\frac{1}{2} + \frac{1}{2}\sin \left[ {\frac{\pi }{{10}}\left( {x - 40} \right)} \right],}&{x \in \left[ {35,45} \right);} \\ {1,}&{x \in \left[ {45,55} \right);} \\ {\frac{1}{2} - \frac{1}{2}\sin \left[ {\frac{\pi }{{10}}\left( {x - 60} \right)} \right],}&{x \in \left[ {55,65} \right].} \end{array}} \right. $ |
| $ {\mu _{11,5}} = \left\{ {\begin{array}{*{20}{c}} {1,}&{x \in \left[ {0,35} \right);} \\ {\frac{1}{2} - \frac{1}{2}\sin \left[ {\frac{\pi }{{10}}\left( {x - 40} \right)} \right],}&{x \in \left[ {35,45} \right].} \end{array}} \right. $ |
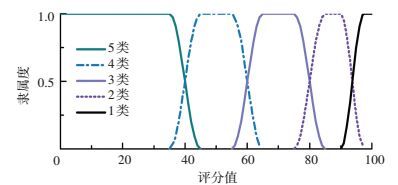
也可根据图 4确定其隶属于评估等级en的隶属度.结合初始基本可信度和权重的计算结果,计算第2层指标的基本可信度,计算公式为
| $ {m_{ij,n}} = \frac{{{w_{ij}}}}{{{w_{\max }}}} \cdot {\mu _{ij,n}}. $ | (1) |
式中:mij, n为指标Pij相对于评估等级en的可信度;wij为指标Pij的权重值;wmax为Pi下的第2层指标中的最大权重值.
|
图 4 第2级指标的分级隶属度 Figure 4 Grade membership of the second class index |
顶层和第1层的基本可信度由下层的证据合成得到.对于T个证据,利用Dempster组合规则合成得到的基本可信度为
| $ {m_{1,{e_n}}} = \frac{{\sum\limits_{\bigcap {{A_i} = A} } {\prod\limits_{i = 1}^T {{m_i}\left( {{A_i}} \right)} } }}{{\sum\limits_{\bigcap {{A_i} \ne Ø} } {\prod\limits_{i = 1}^T {{m_i}\left( {{A_i}} \right)} } }}. $ | (2) |
其中定义识别框架Θ上的基本可信度函数m:2Θ→[0, 1],满足m (∅)=0,∑m(A)=1.
Dempster组合规则的使用条件较严格,要求证据之间必须相互独立且一致,辨识框架中的元素必须互斥且穷尽等,这些条件往往在应用中难以得到满足.另外,在证据高度冲突的情况下,Dempster组合规则的结论可能有悖常理[17].在本文提出的斜拉桥技术状态评估过程中,有可能出现证据冲突的状况,例如外观检查和监测值评估结果差异大,在此情况下使用证据理论进行合成时,易掩盖子指标之间评分差异大的状况.本文结合桥梁上的实际情况给出一种改进的组合规则,尝试解决此类冲突问题.
首先,定义映射M为
| $ M\left( {{m_1}\left( k \right),{m_2}\left( k \right)} \right) = {e_n} \ne Ø . $ |
其中假定m1(k)∩m2(k)=en,或者en⊆m1(k),或者en⊆m2(k).
对于任意的en⊆Θ,以P1指标为例,对应于en等级的两个证据合成的基本可信度计算公式为
| $ {m_{1,{e_n}}} = \frac{{\sum\limits_{M\left( {B,C} \right) = {e_n}} {{m_1}\left( B \right){m_2}\left( C \right)} }}{{\sum\limits_{M\left( {B,C} \right) \in \left( {{2^\Theta }\backslash \mathit{ Ø }} \right)} {{m_1}\left( B \right){m_2}\left( C \right)} }}. $ | (3) |
该方法中,等级允许将一个元素映射到2Θ中的多个元素,能够增强两个证据相似或相悖的状况,进一步提高评估的可靠性.
3 实例验证 3.1 病害检查状况以江苏省2005年建成的某特大跨径钢结构斜拉桥为背景,主桥是钢塔钢箱梁结构,全长1 288 m.经详细检测,此次检测出的病害有:对于斜拉索系统,16.1%的钢护筒出现防护漆脱落,16.7%的阻尼器出现涂层劣化,8.3%下锚头出现防腐油脂渗漏;对于钢箱梁,12%的箱室出现涂装层劣化,单箱室最大劣化率是0.13%,4.2%的箱室出现锈蚀,单箱室最大锈蚀率是0.08%;73.6%的箱室出现斜腹杆开裂,最大裂纹长度达60 cm;对于索塔,55.8%的箱室出现涂装层劣化,单箱室最大劣化率是0.27%,1.9%的箱室出现锈蚀,单箱室最大锈蚀率是0.005%,42.3%的箱室出现螺栓锈蚀或松动,单箱室最大破损率是9.4%;对于桥墩,盖梁有一处混凝土破损,破损面积为0.05 m2;对于支座,31.8%支座出现垫石混凝土破损,轻微螺栓锈蚀、缺失,局部钢垫板锈蚀等病害;对于桥面铺装,局部有油污、坑槽,发现两条较长的纵向裂缝;对于伸缩缝装置,部分橡胶条老化;对于栏杆、护栏,2.3%的护栏出现防护漆脱落,个别出现变形.
可以看出,最为严重的问题为钢箱梁内纵隔板钢管过焊孔处大多出现开裂,局部出现断裂现象;相比钢箱梁,索塔的涂装层缺陷面积和螺栓锈蚀个数均较多;对于斜拉索系统、桥墩、附属设施等,多是轻微病害.
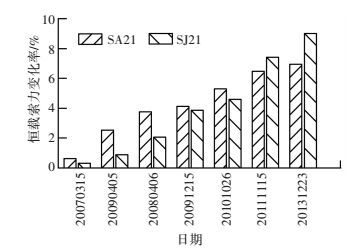
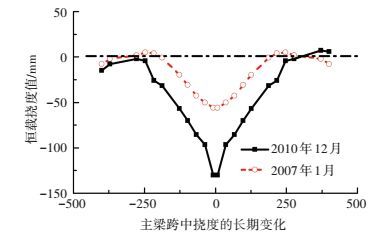
对于该桥的长期监测数据状况:索力出现了轻微的重分布现象[18],图 5中给出南塔两侧最长索的逐年变化情况,可以看出,南塔两侧最长的索分担了其他索的索力,处在一直增长的趋势,2014年达到成桥索力的9%;图 6给出了主梁跨中挠度的变化状况,由于2011年挠度监测传感器全部更换,这里仅给出至2011年的状况,可以看出恒载挠度出现了一定程度的下沉;历年检测到的频率在0.254~0.256 Hz之间变动,结构的频率及阻尼比的变化趋势比较平稳;塔顶偏位暂无异常.
|
图 5 索力的长期变化 Figure 5 Long-term changes of cable forces |
|
图 6 主梁跨中挠度的长期变化 Figure 6 Long-term changes of mid-span deflection for the girder |
综合本次桥梁外观检查结果和监测数据结果,采用基于证据融合的评估方法进行评定.根据相应计算步骤, 首先确定指标的初始基本可信度, 见表 1.
| 表 1 各指标的初始基本可信度 Table 1 Initial basic confidence of each index |
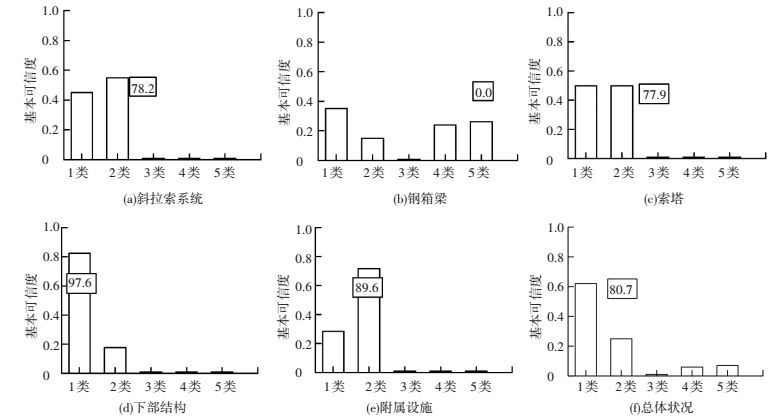
然后按照式 (1)、(3) 对桥梁进行综合评估,得到5大类部件以及总体的最终基本可信度见图 7,而根据评定标准评定方法得到的数值结果亦在图 7中用白框在相应位置标志出来.
|
图 7 既有标准和融合评估方法的主要部件结果对比 Figure 7 Comparison of results based on existing standards and fusion evaluation methods for main components |
根据图 7的结果,对比融合评估方法和既有标准评估方法可以看出,两者存在一定差别.在斜拉索系统、钢箱梁和索塔方面,两者差别较大,在下部结构和附属设施方面,两者较相近. 1) 对于钢箱梁,钢箱梁出现了少量涂层劣化和较多腹杆开裂,但是结构并未发现明显永久性变形,振动特性良好,将其归为5类则过严.在融合评估结果中,钢箱梁外观检查偏于4、5类,线形偏于2类,振动频率属1类,可信度集合分布也反映出子指标存在差异大的情况.对于索塔,采取的是小型修补工程,应该属于2类,评定标准中同一构件多种病害的合成分数低很多,造成了评分低的结果.另外,索塔的子指标之间存在冲突状况,外观检查状况较恶劣,塔顶偏位状况较好,因而合成的可信度较低.这种情形提醒管理人员需进一步检查子指标的评定结果,便于作出更准确的决策.斜拉索系统有相似的结论. 2) 对于下部结构、附属设施,多是轻微病害,大多可以采取保养、局部小修的方案予以处置.两者评定结果相似,但是本文的附属设施的子项目包含更多信息.
综合来看,斜拉桥总体状况良好.本文通过融合评估方法计算得到的类别属向更为合理,且可信度集合相比一个得分值更能综合地表达结构的状况.
4 结论1) 考虑斜拉桥部件的全面性以及部分长期监测数据,建立了新的斜拉桥评估指标体系,指标体系在目标层以下设置了3层:第1层突出斜拉桥五大部件;第2层为更细化些的子部件项目;第3层为病害层.
2) 提出了一种分段线性的指标评定标准,该方式能够更好反映不同程度病害的扣分值.
3) 建立了一种基于证据融合的评定方法和相应的流程图.初始基本可信度由岭型分布的模糊隶属度决定, 结合初始基本可信度和权重的计算结果, 得到第2层指标的基本可信度,顶层和第1层的基本可信度通过改进的证据合成规则融合得到.
4) 以江苏省特大跨径钢结构斜拉桥第10年的定期检查报告中的病害和长期监测数据为基准,分别用融合评估方法以及评定标准的方法计算.结果表明,用融合评估方法计算得到的类别属向更合理,与病害程度和维修状况一致,能更综合地表达结构的技术状况.
| [1] | AKGUL F. Development of a bridge management system incorporating a newly developed model for element condition evaluation based on damage effects[J]. Structure and Infrastructure Engineering, 2013, 9(12): 1206-1224. DOI: 10.1080/15732479.2012.674536 |
| [2] |
陕西省公路局. 公路桥涵养护规范: JTG H11—2004[S]. 北京: 人民交通出版社, 2004.
Shaanxi Highway Bureau. Code for maintenance of highway bridges and culvers:JTG H11—2004[S].Beijing:China Communication Press, 2004. |
| [3] |
交通运输部公路科学研究院. 公路桥梁技术状况评定标准: JTG/T H21—2011[S]. 北京: 人民交通出版社, 2011.
Research Institute of Highway Ministry of Transport. Standards for technical condition evaluation of highway bridges:JTG/T H21—2011[S]. Beijing: China Communication Press, 2011. |
| [4] | HUANG Yinghua, ADAMS T M, PINCHEIRA J A. Analysis of life-cycle maintenance strategies for concrete bridge decks[J]. Journal of Bridge Engineering, 2004, 9(3): 250-258. DOI: 10.1061/(ASCE)1084-0702(2004)9:3(250) |
| [5] |
杨风暴, 王肖霞.
D-S证据理论的冲突证据合成方法[M]. 北京: 国防工业出版社, 2010: 50-54.
YANG Fengbao, WANG Xiaoxia. Combination method of conflictive evidences in D-S evidence theory[M]. Beijing: National Defend Industry Press, 2010: 50-54. |
| [6] |
聂功武, 孙利民. 桥梁养护巡检与健康监测系统信息的融合[J].
上海交通大学学报, 2011, 45(Sup1): 104-108.
NIE Gongwu, SUN Limin. Integration of inspection and structural health monitoring system for bridge management[J]. Journal of Shanghai Jiaotong University, 2011, 45(Sup1): 104-108. |
| [7] |
任远, 王晓春, 黄侨, 等. 中美欧公路桥梁设计规范的综合评价方法[J].
哈尔滨工业大学学报, 2016, 48(9): 7-13.
REN Yuan, WANG Xiaochun, HUANG Qiao, et al. The comprehensive evaluation method of highway bridge design specifications ofChina, U.S. and Europe[J]. Journal of Harbin Institute of Technology, 2016, 48(9): 7-13. DOI: 10.11918/j.issn.0367-6234.2016.09.002 |
| [8] | MOKHTARI K, REN Jun, ROBERTS C, et al. Decision support framework for risk management on sea ports and terminals using fuzzy set theory and evidential reasoning approach[J]. Expert Systems with Applications An International Journal, 2012, 39(5): 5087-5103. DOI: 10.1016/j.eswa.2011.11.030 |
| [9] | JIANG Shaofei, FU Chun, WU Zhaoqi. Intelligent data-fusion model using correlation fractal dimension for structural damage identification[J]. Advanced Materials Research, 2010, 143-144: 1300-1304. DOI: 10.4028/www.scientific.net/AMR.143-144 |
| [10] |
汪炳, 黄侨, 刘小玲. 疲劳荷载作用下栓钉连接件的抗剪承载力退化规律[J].
哈尔滨工业大学学报, 2016, 48(9): 76-82.
WANG Bing, HUANG Qiao, LIU Xiaoling. Shear capacity degradation law of stud connectors under fatigue loading[J]. Journal of Harbin Institute of Technology, 2016, 48(9): 76-82. DOI: 10.11918/j.issn.0367-6234.2016.09.014 |
| [11] | BAO Yuequan, XIA Yong, LI Hui, et al. Data fusion-based structural damage detection under varying temperature conditions[J]. International Journal of Structural Stability & Dynamics, 2013, 12(6): 67-75. |
| [12] | ZHOU Yunlai, FIGUEIREDO E, MAIA N, et al. Damage detection in structures using a transmissibility-based Mahalanobis distance[J]. Structural Control & Health Monitoring, 2015, 22(10): 1209-1222. |
| [13] | NELSON M S, FAM A Z, BUSEL J P, et al. Fiber-reinforced polymer stay-in-place structural forms for concrete bridge decks: state-of-the-art review[J]. Aci Structural Journal, 2014, 111(5): 1069-1080. |
| [14] | BOLAR A, TESFAMARIAM S, SADIQ R. Condition assessment for bridges:a hierarchical evidential reasoning (HER) framework[J]. Structure and Infrastructure Engineering, 2013, 9(7): 648-666. DOI: 10.1080/15732479.2011.602979 |
| [15] | WANG Yingming, ELHAG T M S. Evidential reasoning approach for bridge condition assessment[J]. Expert Systems with Applications, 2008, 34(1): 689-699. DOI: 10.1016/j.eswa.2006.10.006 |
| [16] |
廖瑞金, 黄飞龙, 杨丽君, 等. 多信息量融合的电力变压器状态评估模型[J].
高电压技术, 2010, 36(6): 1455-1460.
LIAO Ruijin, HUANG Feilong, YANG Lijun, et al. Condition assessment of power transformer using information fusion[J]. High Voltage Engineering, 2010, 36(6): 1455-1460. |
| [17] | SUN Xiaoyan, MAHADEVAN S, HAN Wenhua, et al. Combining dependent bodies of evidence[J]. Applied Intelligence, 2016, 44(3): 634-644. DOI: 10.1007/s10489-015-0723-5 |
| [18] |
任远, 刘小玲, 黄侨. 斜拉桥恒载索力长期变化趋势分析与评估[J].
哈尔滨工业大学学报, 2015, 47(6): 103-108.
REN Yuan, LIU Xiaoling, HUANG Qiao. The long-term analysis and assessment of the cable forces due to dead load in cable-stayed bridges[J]. Journal of Harbin Institute of Technology, 2015, 47(6): 103-108. DOI: 10.11918/j.issn.0367-6234.2015.06.019 |
 2017, Vol. 49
2017, Vol. 49


