2. 哈尔滨工业大学 交通科学与工程学院,哈尔滨 150090
2. School of Transportation Science and Engineering, Harbin Institute of Technology, Harbin 150090, China
交通拥堵收费理论最早起源于上世纪20年代[1],文献[2-3]提出了基于经济学上边际成本定价理论的拥堵收费,达到理论与技术的成熟阶段则是80年代之后.文献[4-10]虽早已对拥挤收费策略进行研究,然而很多研究都着眼于拥挤收费的费率、收费机制、收费策略对出行行为的影响等方面,对于拥挤收费改善效果的研究相对薄弱.
中国还没有拥堵收费政策的成功案例,对拥堵收费政策的研究大部分均停留在理论阶段,研究内容和国外较为一致.文献[11]对道路拥挤收费的基本原理进行了分析;文献[12]对费额分配理论进行了研究;文献[13]对进行拥挤收费方案事前评价时应包括的内容和采用的方法进行研究;文献[14]对伦敦的收费实践效果进行了评价并作了相关思考.可见,中国同样缺乏对拥堵收费措施改善效果的评价研究.
1 拥堵收费改善效果评价方法考虑到拥堵收费仅改变了局部出行路径和出行方式的出行成本,并未对区域总的交通生成造成明显影响,因此拥堵收费下的交通分配可以归结为路阻函数的变化而引起的交通重分配.
1.1 拥堵收费下的阻抗函数主要路阻函数包括[15]:美国联邦公路局路阻函数模型[16]、Davidson路阻函数模型[17]、日本和德国的线型路阻函数模型和回归路阻模型.本文从成本出发,以现有道路交通网络的交通分配路径选择理论为基础,以广义交通阻抗为参照,构建拥堵收费下的阻抗函数.
出行成本不仅是支付的货币成本,而是综合考虑了时间、经济费用等因素的广义成本,又称为综合成本Cs(synthetic cost).以出行者的出行时间、一般经济费用 (油费、票价、燃油税等) 和附加费用为因素构建出行者出行方式和出行路径选择的综合成本,其数学表达式为
| $ {C_{sij}} = \left[ {r \times {T_{ij}} + {E_{ij}} + {C_{{\rm{a}}ij}}} \right] \times {f_i} \times {f_j}. $ | (1) |
式中:i为可选路径编号,j为交通方式编号,Csij为第i条路径上j交通方式的综合成本,Tij为第i条路径上j交通方式的出行时间价值,Eij为第i条路径上j交通方式的一般出行费用,Caij为第i条路径上j交通方式的附加出行费用,r为时间价值相对于基本费用的权重,fi为第i条路径的修正系数,fj为j交通方式的修正系数.
fi和fj的引入主要是考虑到不同路径在道路里程、等级、交通管理方式等方面存在着很大差异,不同出行方式也在便捷性、灵活性、安全性方面存在不同,出行决策会受到这些因素的影响,甚至出行习惯也会对最终决策有所影响.考虑到出行路径和出行方式的一些非量化属性等因素对路径选择和出行方式选择的影响,阻抗函数中引入了路径修正系数fi和交通方式修正系数fj.由式 (1) 可知,该阻抗函数的确定将路径选择和出行方式选择融合为同一选择过程.
1.2 阻抗函数参数标定的方法1) 权重参数r.权重r体现了出行时间和费用在综合成本中的重要性,可根据出行者的意愿调查数据进行标定,出行者的首要考虑条件是时间因素还是费用因素决定r的取值.
2) 出行时间价值T.假设出行者将出行时间用于工作,可根据个人的固定收入计算单位时间价值从而估计出行时间的机会成本大小,出行时间价值表达式为
| $ T = t \times \theta . $ | (2) |
式中t为出行时间长度,θ为出行者的单位时间价值.
对于个体而言单位时间价值是不同的,可根据个人的年收入、年工作时间、日工作时间推算.关于出行时间长度t,美国公路局提出了应用较广的BPR函数,但实践证明该函数在中国的应用还存在较大误差,文献[18]通过研究推导了路段流量和通行时间之间的关系,并与BPR函数进行了差异分析,得出了优化后 (相关系数0.99) 的关于路段流量和行驶时间关系的拟合方程,表达式为
| $ {t_{\rm{r}}} = {t_0}\left[ {1 + 0.5668{{\left( {\frac{q}{c}} \right)}^{1.4431}}} \right]. $ | (3) |
式中:tr为交通量q下路段的行驶时间,t0为畅通流状态下路段的行驶时间,q为路段车流量,c为路段通行能力.
式 (3) 可用于计算实施拥堵收费后路段的行驶时间变化,私人小汽车出行时间长度可以认为等于路段行驶时间,但对于公共交通,出行时间还应包括站台等待时间,因此总的出行时间长度可以表示为
| $ t = {t_{\rm{r}}} + \lambda \times {t_{\rm{w}}} = {t_{\rm{r}}} + \lambda \times \frac{1}{{2f}}. $ | (4) |
式中:tw为站台等待时间,f为公交的发车频率,λ为站台等待时间相对于路段行驶时间的权重.
站台时间相对于路段行驶时间的权重λ可通过公交出行者的意向调查获取,总结以上分析最终得到时间价值的表达式为
| $ T = \left[ {{t_{\rm{r}}} + \lambda \times \frac{1}{{2 \times f}}} \right] \times \theta . $ | (5) |
3) 一般出行费用E和附加出行费用Ca.一般出行费用E包括油费、票价等,出行附加费用Ca是指由于出行的特殊性而额外增加的费用,主要指拥堵收费.
公共交通使用者只需要支付定额票价,因此公交出行的一般费用等于公交票价.私家车出行者一般出行费用即为燃油费,根据车公里燃油费η可计算一般费用为
| $ E = L \times \eta . $ | (6) |
式中L为行驶里程,η为车公里燃油费用.
4) 路径修正系数fi和交通方式修正系数fj.路径修正系数fi和交通方式修正系数fj可根据现状不同路径上不同出行方式的组成结构进行标定.
1.3 交通分配模型构建假设出行者完全理性,且获得的交通信息全面、均衡,那么决策过程中,选择某路径和某交通方式就取决于路径上该出行方式的效用值U (utility).而出行者决策中的唯一依据就是综合成本Cs.综合成本越高,出行者选择的几率越低,即路径上出行方式的效用值越低,所以效用值和综合成本成反比关系,因此效用值可用综合成本表示为
| $ {U_{ij}} = \frac{1}{{{C_{{\rm{s}}ij}}}}. $ | (7) |
本文采用Logit模型作为路径和出行方式选择的分配模型,考虑到常规Logit模型的假设前提过于理想化,而实际中出行者不可能对所有备选方案的效用值都能作出准确的估计.考虑出行者对不同选择枝的敏感度,在常规Logit模型中引入Kirchhoff参数,模型表达式为
| $ \begin{array}{l} {P_{ij}} = \frac{{\exp \left( {k \times \log {U_{ij}}} \right)}}{{\sum\limits_i {\sum\limits_j {\exp \left( {k \times \log {U_{ij}}} \right)} } }} = \\ \;\;\;\;\;\;\;\frac{{\exp \left( { - k \times \log {C_{{\rm{s}}ij}}} \right)}}{{\sum\limits_i {\sum\limits_j {\exp \left( { - k \times \log {C_{{\rm{s}}ij}}} \right)} } }}. \end{array} $ | (8) |
式中Pij为出行者选择第i条路径上j出行方式的概率,k为Kirchhoff分布的参数,Kirchhoff分布参数的不同取值反应了出行者敏感度的程度,该参数可根据现状交通流数据进行反复验证标定.
2 拥堵收费虚拟案例及数据采集 2.1 拥堵收费虚拟方案以南京市应天大街高架桥 (龙蟠南路至江东中路区段) 为拥堵收费路段,构建拥堵收费区域虚拟实施场景,拟采用静态收费方式,收费时段为16:30—19:00,仅对由东向西小汽车交通 (不包括出租车) 进行拥堵收费,收费额度从5元/次到20元/次划分7个层次探讨实施拥堵收费可能带来的改善效果.
2.2 交通调查和数据分析 2.2.1 出行路径分析在收费路段影响区域内存在多条和应天大街高架收费路段具有类似交通功能的出行路径,经分析确定受影响的出行路径主要包括以下3条:1) 路径1为应天大街高架,虚拟收费路段;2) 路径2为应天大街 (高架桥下地面道路),位于收费路段正下方,全线共9个交叉口均采用信号控制;3) 路径3为龙蟠南路—雨花南路—梦都大街—江东中路,沿线12个交叉口均采用信号控制.这3条路径的基本参数见表 1.
| 表 1 现状高峰时段下拥堵收费影响区域内主要出行路径的基本参数 Table 1 Basic parameters of the main travel paths within congestion pricing's influence area during peak period |
小汽车出行方式:同一出行目的下,3条路径都可供小汽车出行者选择.
公交出行方式:若应天大街高架上小汽车出行者改变出行方式而使用公交车出行,可供使用的公交车路线有126路、14路、103路、110路转39路以及110路转浦新线.
2.2.3 交通量数据路径1:高峰时段主要交通量为东西向直行,路径1由东向西方向路段的平均交通量为3 628 pcu/h,其中出行路径覆盖整个收费路段的的小汽车交通量为2 335 pcu/h.
路径2:平均交通量为2 617 pcu/h,但部分交通流仅利用了路径2的部分路段,通过进一步分析得到在路径2上行驶的由东向西的交通量为1 764 pcu/h.
路径3:平均交通量为2 482 pcu/h,通过进一步分析得到在路径3上行驶的由东向西的交通量为1 322 pcu/h.
公交出行:高峰时间内目标公交线路共发车39个班次,大部分均处于满载状态,经统计得到累计乘客约2 058人,中途累计下客数392人,最终得到收费区间内的公交出行量约为1 666人/h.
通过抽样调查统计得到小汽车高峰时间段的满载率为1.8人/车,再根据以上分析可知,符合本文起终点要求的交通出行总量中,路径1所占出行比例P1c=0.37,路径2所占出行比例P2c=0.29,路径3所占出行比例P3c=0.21,公交出行方式所占出行比例Pb=0.15.
3 拥堵收费的改善效果评价 3.1 交通分配模型参数的标定 3.1.1 权重参数r经SP调查数据可知,公众在选择出行方式时将出行时间作为首要考虑因素的人数比重为67%.因此,r=67%/(1-67%)=2.03.
3.1.2 单位时间价值参数θ南京市统计局发布的“2012年南京市国民经济和社会发展统计公报”显示,2012年南京市城市居民人均可支配收入达到36 322元,而国家法定工作时间为全年工作250 d,每天工作8 h,因此南京市人均时间价值θ=年收入/(年工作时间×日工作时间×60)=0.303元/min.
3.1.3 时间长度t公交出行虽然存在线路和里程的差异,但总体车内时间差异不大,根据现状调查可知公交出行方式的平均行程时间为42 min,各站台的平均等待时间为10.8 min,而SP调查结果显示认为相对于车上时间认为站台等待时间更加难以忍受的公众比率为59.7%,站台等待时间相对于车上行驶时间的权重λ可表示为λ=59.7%/(1-59.7)=1.48.因此公交出行方式的时间长度tb可表为tb=tr+λ×tw=42+1.48×10.8=57.98.
根据对小汽车出行调查可知,3条路径在畅通状态下的行驶时间分别为6.3、8.7、12.2 min,结合3条路径的里程可得到畅通状态下的速度取整后约为58、42、45 km/h,基本符合城市道路交通现状.结合出行路径分析中关于不同路径现状高峰时段交通流量和行程时间的数据,代入式 (3)~(5) 可以得到3条主要路径路段流量和行驶时间的拟合公式分别为
| $ {t_{1{\rm{c}}}} = 6.3\left[ {1 + 0.5668{{\left( {\frac{{{q_1}}}{{3920}}} \right)}^{1.4431}}} \right], $ | (9) |
| $ {t_{2{\rm{c}}}} = 8.7\left[ {1 + 0.5668{{\left( {\frac{{{q_1}}}{{3400}}} \right)}^{1.4431}}} \right], $ | (10) |
| $ {t_{3{\rm{c}}}} = 12.2\left[ {1 + 0.5668{{\left( {\frac{{{q_1}}}{{3250}}} \right)}^{1.4431}}} \right]. $ | (11) |
其中q1、q2、q3分别为路径1、路径2、路径3上总的交通量.
3.1.4 一般出行费用E小汽车的一般费用E主要指燃油费,考虑到本文研究的路段长度约为6 km和9 km,差异不显著,本文通过问卷调查估算不同路径的车公里油费率η.调查得出信号控制路段上车公里燃油费率η均值为0.92元/km,无信号控制路段上车公里燃油费率η均值为0.73元/km.公交车出行的费用E仅为公交票价,本次研究公交线路的票价均为1元/次.
3.1.5 修正系数及Kirchhoff分布参数k考虑到路径和出行方式的修正系数都是相对指标,因此需要分别为路径和出行方式划定相对基准.分别假设路径1(基准路径) 的修正系数为f1=1,路径2的修正系数为f2,路径3的修正系数为f3,小汽车出行方式 (基准出行方式) 的修正系数为fc=1,公交车出行方式的修正系数为fb.根据本文构建的交通分配模型可得到如下关系式.
路径i(i=1, 2, 3) 上的小汽车分担率为
| $ {P_{i{\rm{c}}}} = \frac{{\exp \left( { - k \times \log {C_{{\rm{s}}i{\rm{c}}}}} \right)}}{{\sum\limits_i {\exp \left( { - k \times \log {C_{{\rm{s}}i{\rm{c}}}}} \right)} + \exp \left( { - k \times \log {C_{{\rm{sb}}}}} \right)}}. $ | (12) |
公交出行方式分担率为
| $ {P_{\rm{b}}} = \frac{{\exp \left( { - k \times \log {C_{{\rm{sb}}}}} \right)}}{{\sum\limits_i {\exp \left( { - k \times \log {C_{{\rm{s}}i{\rm{c}}}}} \right)} + \exp \left( { - k \times \log {C_{{\rm{sb}}}}} \right)}}. $ | (13) |
各出行方式分担率之后为1,即
| $ \sum\limits_{i = 1}^3 {{P_{i{\rm{c}}}} + {P_{\rm{b}}}} = 1. $ | (14) |
各路径和出行方式的综合成本为
| $ {C_{{\rm{s}}i{\rm{c}}}} = \left[ {2.03 \times {T_{i{\rm{c}}}} + {E_{i{\rm{c}}}}/1.8} \right] \times {f_i} \times {f_{\rm{c}}}, $ | (15) |
| $ {C_{{\rm{sb}}}} = \left[ {2.03 \times {T_{\rm{b}}} + {E_{\rm{b}}}} \right] \times {f_{\rm{b}}}. $ | (16) |
各路径和出行方式的时间价值为
| $ {T_{i{\rm{c}}}} = {t_{i{\rm{c}}}} \times \theta = 0.303 \times {t_{i{\rm{c}}}}, $ | (17) |
| $ {T_{\rm{b}}} = {t_{\rm{b}}} \times \theta = 0.303 \times {t_{\rm{b}}}. $ | (18) |
通过编程对该方程组进行求解,最终得到最优解:f2=0.78;f3=0.53;fb=0.84;k=1.27.由标定结果可知,路径2和路径3相对于路径1的修正系数分别为0.78、0.53,即考虑路径修正的影响后两条路径的综合成本是降低的.可见,虽然路径1相对于路径2、路径3具有一定优势,但路径1最大的优势是在时间和费用上,其他方面并不是很明显,因此当其他因素被考虑在内后,路径1的总体优势会出现弱化.
3.2 拥堵收费下的交通重分配通过对采用的交通分配模型的参数进行标定,最终得到拥堵收费下不同路径的综合成本表达式如下,Cs1c、Cs2c、Cs3c分别为路径1、路径2、路径3上小汽车出行的综合成本,Csb为公共交通出行的综合成本,在表达式中Q1、Q2、Q3为受拥堵收费影响下各条路径上的分配出行量,Ca为附加到路径1上的拥堵费用.
| $ \begin{array}{l} {C_{{\rm{s}}1{\rm{c}}}} = 2.03 \times 6.3\left[ {1 + 0.5668{{\left( {\frac{{1293 + \frac{{{Q_1}}}{{1.8}}}}{{3920}}} \right)}^{1.4431}}} \right] + \\ \;\;\;\;\;\;\;\;\;\frac{{6.1 \times 0.73}}{{1.8}}, \end{array} $ |
| $ \begin{array}{l} {C_{{\rm{s}}2{\rm{c}}}} = \left[ {2.03 \times 8.7\left[ {1 + 0.5668{{\left( {853\frac{{1293 + \frac{{{Q_2}}}{{1.8}}}}{{3400}}} \right)}^{1.4431}}} \right] + } \right.\\ \;\;\;\;\;\;\;\;\;\left. {6.1 \times 0.92/1.8} \right] \times 0.78. \end{array} $ |
| $ \begin{array}{l} {C_{{\rm{s}}3{\rm{c}}}} = \left[ {2.03 \times 12.2\left[ {1 + 0.5668{{\left( {\frac{{1160 + \frac{{{Q_3}}}{{1.8}}}}{{3250}}} \right)}^{1.4431}}} \right] + } \right.\\ \;\;\;\;\;\;\;\;\;\left. {9.2 \times 0.92/1.8} \right] \times 0.53, \end{array} $ |
| $ \begin{array}{l} {C_{{\rm{sb}}}} = \left[ {2.03 \times {T_{\rm{b}}} + {E_{\rm{b}}}} \right] \times {f_4} \times {f_{\rm{b}}} = \left[ {2.03 \times 55.98 + } \right.\\ \;\;\;\;\;\;\;\;\;\left. 1 \right] \times 0.84. \end{array} $ |
对路径1加载拥堵收费费用后,路径1的综合成本Cs1c变大,选择路径1进行出行的比例会降低,而其他路径的综合成本降低,吸引的交通量会增大,在交通量的不断重分配过程中4条路径会重新达到新的平衡,使得满足:
| $ \begin{array}{l} {P_{i{\rm{c}}}} = \frac{{\exp \left( { - 1.27 \times \log {C_{{\rm{s}}i{\rm{c}}}}} \right)}}{{\sum\limits_i {\exp \left( { - 1.27 \times \log {C_{{\rm{s}}i{\rm{c}}}}} \right)} + \exp \left( { - 1.27 \times \log {C_{{\rm{sb}}}}} \right)}} = \\ \;\;\;\;\;\;\;\;\frac{{{Q_i}}}{Q},\\ {P_{\rm{b}}} = \frac{{\exp \left( { - 1.27 \times \log {C_{{\rm{sb}}}}} \right)}}{{\sum\limits_i {\exp \left( { - 1.27 \times \log {C_{{\rm{s}}i{\rm{c}}}}} \right)} + \exp \left( { - 1.27 \times \log {C_{{\rm{sb}}}}} \right)}} = \\ \;\;\;\;\;\;\;\;\frac{{{Q_4}}}{Q}. \end{array} $ |
在不同的拥堵收费费额Ca下,最终交通分配达到的平衡也是不同的,不同收费额度下平衡状态时各路径的分配出行量见表 2.
| 表 2 不同收费额度下的交通出行量分配平衡状态 Table 2 Equilibrium state under different pricing rates |
1) 交通出行量分布评价. 图 1为不同收费费率下的交通出行量平衡态曲线, 随着收费额度的增加,路径1(收费路径) 出行量显著减少,而其他路径则呈现递增趋势;从出行量变化的趋势分析,收费额度为0~10元/次时,路径出行量的变化率更高,说明收费费率超过一定额度时,费率的增加在诱导交通重新分配上的效力会逐渐降低.

|
图 1 不同收费费率下的交通出行量平衡态曲线 Figure 1 Traffic volume's equilibrium state under different charging fee |
2) 出行方式分担率评价. 图 2为公交出行方式分担率变化曲线,随着拥堵收费措施的实施,公交分担率升高.但从拟合曲线的斜率可以发现,相对于收费措施费率的变化,公交出行方式分担率的变化程度并不显著.

|
图 2 公交出行方式分担率变化曲线 Figure 2 Variation of public transportation's share rate |
3) 道路服务水平评价. 图 3为各路径的道路饱和度曲线, 拟采用拥堵收费措施的路径1随着拥堵费率的提高,道路饱和度会有明显降低.然而当拥堵费率超过8元/次时,路径2的饱和度将超过0.9(E级服务水平,属于不稳定车流,交通拥挤延误很大,司机无法忍受),当拥堵费率超过15元/次时,路径3的饱和度也将超过0.9,此时路径2的饱和度更是高达0.982,接近饱和.
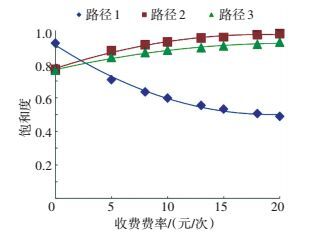
|
图 3 各路径的道路饱和度曲线 Figure 3 Relationship curves of each path's road saturation |
4) 行程速度评价. 图 4为各路径的平均行程速度曲线, 3条路径的行程时间随着路径上交通量的变化而改变,由于3条路径长度差异较小,因此行程时间长度变化不大.行程时间转化为行程速度时可以发现,路径1的行程速度在拥堵费用为5元/次时的变化较为明显,随着费率的增加变化逐渐趋于平缓.
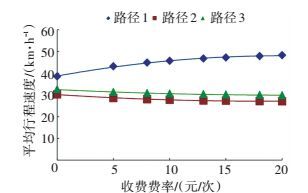
|
图 4 各路径的平均行程速度曲线 Figure 4 Relationship curves of each path's average speed |
1) 拥堵收费对交通改善具有直接影响,但影响程度和拥堵费率并非简单的正比关系,总体上,拥堵费率处于10元/次以下时各指标的变化率明显高于费率大于10元/次时的变化率,因此从单位费用的改善效率来看10元/次以内的收费费率的效率更高.
2) 拥堵收费的影响程度受到收费费率的直接制约,收费费率过高时甚至会出现负面影响.研究认为,拥堵收费费额不应超过8元/次,且在收费标准划分层次下拥堵收费费额为5元/次时改善效果最佳.
3) 从拥堵收费下不同出行选择上的出行量分布和服务水平变化可以看出拥堵收费措施能够诱导路网交通量的重新分布.可以认为一定费额下拥堵收费措施在缓解交通拥堵方面是具有积极的影响,且效果较为明显.
4) 从公交分担率和行程速度上可以认为拥堵收费措施对提高城市交通系统的利用率和提高效率是积极的.
5) 从不同出行选择的出行量、道路服务水平、公交分担率上分析可知,拥堵收费措施在合理的拥堵费用下对交通有明显的改善效果,可以认为该措施在客观可行性方面是有效且可行的.
| [1] |
许方磊, 万涛. 道路拥挤收费理论与城市交通可持续发展[J].
山西科技, 2004(6): 76-77.
XU Fanglei, WAN Tao. The crowded road's fee charging theory and the sustainable development of the urban traffic[J]. Shanxi Science and Technology, 2004(6): 76-77. DOI: 10.3969/j.issn.1004-6429 |
| [2] | KNIGHT F H. Some fallacies in the interpretation of social cost[J]. Quarter Journal of Economics, 1924, 38(4): 582-585. DOI: 10.2307/1884592 |
| [3] | PIGOU A C. The economics of warfare[J]. American Economic Review, 1961, 106(11): 54-56. |
| [4] | VICKERY W S. Congestion theory and transport investment[J]. American Economic Review, 1969, 59(2): 251-260. |
| [5] | HENDESON J V. Road congestion: a reconsideration of pricing theory[J]. Urban Economics, 1974, 1(3): 346-365. DOI: 10.1016/0094-1190(74)90012-6 |
| [6] | COHEN Y. Commuter welfare under peak-period congestion toll: who gains and who lose[J]. International Journal of Transport Economics, 1987, 14(3): 239-266. |
| [7] | ELIASSON J, MATTSSON L G. Equity effects of congestion pricing: Quantitative methodology and a case study for Stockholm[J]. Transportation Research Part A: Policy and Practice, 2006, 40(7): 602-620. DOI: 10.1016/j.tra.2005.11.002 |
| [8] | AMOTT R, PALMA A D, LINDSEY R. Departure time and route choice for the morning commute[J]. Transportation Research B, 1990, 24(3): 209-228. DOI: 10.1016/0191-2615(90)90018-T |
| [9] |
肖恢翚, 孙祥龙, 陆建. 拥挤收费措施的公众可接受性与有效性[J].
哈尔滨工业大学学报, 2014, 46(6): 111-115.
XIAO Huihui, SUN Xianglong, LU Jian. Public acceptability and effectiveness of congestion pricing[J]. Journal of Harbin Institute of Technology, 2014, 46(6): 111-115. DOI: 10.11918/j.issn.0367-6234.2014.06.020 |
| [10] |
孙祥龙, 陆建. 基于结构方程的拥挤收费公众可接受性模型[J].
哈尔滨工业大学学报, 2012, 44(12): 140-144.
SUN Xianglong, LU Jian. Public acceptability model of congestion pricing based on structural equation model[J]. Journal of Harbin Institute of Technology, 2012, 44(12): 140-144. DOI: 10.11918/j.issn.0367-6234.2012.12.025 |
| [11] |
朱广芹, 佟光霁, 代磊磊. 城市道路交通拥挤收费的博弈分析[J].
系统工程理论与实践, 2009, 29(7): 147-152.
ZHU Guangqin, TONG Guangji, DAI Leilei. Algorithm of urban road congestion pricing with game theory[J]. Systems Engineering-Theory & Practice, 2009, 29(7): 147-152. DOI: 10.3321/j.issn:1000-6788 |
| [12] |
丁岳维. 路网收费及费额分配理论研究[D]. 西安: 长安大学, 1999.
DING Yuewei. Theoretical studies of highway network toll and distrvibution of tool sum [D]. Xi'an: Chang'an University, 1999. |
| [13] |
张澍. 城市中心区拥挤收费方案的事前评价研究[D]. 北京: 北京工业大学, 2007.
ZHANG Shu. Prior evaluation research on urban center congestion pricing [D]. Beijing: Beijing University of Technology, 2007. |
| [14] |
颜艳, 杨英姿. 伦敦交通拥挤收费的实施效果及相关思考[J].
城市公用事业, 2009(1): 12-14.
YAN Yan, YANG Yingzi. Implementation effect and relevant thought on London congestion pricing[J]. Urban Public Utility, 2009(1): 12-14. DOI: 10.3969/j.issn.1001-599X |
| [15] |
汪涓. 综合路阻建模与应用研究[D]. 成都: 西南交通大学, 2006.
WANG Juan. Research of synthesis impendence function [D]. Chengdu: Southwest Jiaotong University, 2006. |
| [16] |
郑远, 杜豫川, 孙立军. 美国联邦公路局路阻函数探讨[J].
交通与运输 (学术版), 2007(1): 24-26.
ZHENG Yuan, DU Yuchuan, SUN Lijun. Consideration on problems in the BPR function[J]. Traffic & Transportation (Academic Edition), 2007(1): 24-26. |
| [17] |
王炜, 张桂红. 城市道路实用路阻函数研究[J].
重庆交通学院学报, 1992, 11(3): 84-92.
WANG Wei, ZHANG Guihong. Research on impendence function of urban streets[J]. Journal of Chongqing Jiaotong Institute, 1992, 11(3): 84-92. DOI: 10.7666/d.y1244327 |
| [18] |
王树盛, 黄卫, 陆振波. 路阻函数关系式推导及其拟合分析研究[J].
公路交通科技, 2006, 23(4): 107-110.
WANG Shusheng, HUANG Wei, LU Zhenbo. Deduction of link performance function and its regression analysis[J]. Journal of Highway and Transportation Research and Development, 2006, 23(4): 107-110. DOI: 10.3969/j.issn.1002-0268.2006.04.026 |
 2017, Vol. 49
2017, Vol. 49


