2. 北京工业大学 道路与桥梁工程研究所,北京 100124
2. Institute of Road and Bridge Engineering, Beijing University of Technology, Beijing 100124, China
涡激振动是一种广泛存在于工程领域的非线性振动现象.已有健康监测资料表明,大跨度桥梁较易出现涡激振动现象[1-3],必须在设计阶段对其涡振性能进行准确研究.现有涡振研究仍需依赖物理风洞试验手段,通过弹性悬挂节段模型或全桥气弹模型对其涡振性能进行判定[4-5].然而由于模型加工误差或悬挂弹簧的影响,气弹模型或节段模型不可避免地与实际结构在阻尼比等方面存在某些偏差.由于结构涡振性能受模型质量-阻尼系数影响明显,通过风洞试验获得的结构涡振响应仅能反映试验模拟质量-阻尼系数工况下的结构涡振性能,无法覆盖其他未进行模拟的质量-阻尼系数工况.实际结构涡振可发生模态有多阶,各阶模态质量或模态阻尼比并不一致,若要完全掌握结构涡振性能,需对涡振可发生的各阶模态进行研究,这将带来较大的试验工作量.
为避免上述工作量,研究人员期望通过引入某些数学模型来模拟结构涡振现象,并利用该数学模型计算不同质量-阻尼系数工况下的结构涡振响应.文献[6]最早基于Van der Pol振子的概念,提出了经验非线性模型来描述桥梁断面涡激振动现象.后续又有许多学者在此基础上提出了许多改进形式,如:经验线性模型及广义非线性模型等[7-10].可惜现有经验模型都是从模拟结构自限幅振动特性出发,模型参数需通过拟合试验获得的结构自限幅振动响应获得.由于结构自限幅振动响应受结构质量-阻尼系数影响明显,因此现有涡振模型更多的是描述一种已经发生的涡振现象,而难以用来预测其他未进行试验的工况.
导致结构出现涡激振动的主要原因是结构受到的非线性气动效应.如果能通过试验手段获得结构涡振过程中所受气动效应特性,并利用某些数学模型模拟该效应,将该数学模型与结构运动方程结合后,理论上可用来计算不同参数 (质量-阻尼系数) 下的结构涡振响应.从这个角度出发,或许可突破现有方法的局限,以较小的工作量完成对结构各阶涡振性能的完全掌握.实现上述目的的关键在于结构涡振气动效应特性识别,因此本文有针对性的提出了相应识别方法,并以实际桥梁断面风洞试验为背景对上述方法进行了详细验证.本文首先介绍涡振气动效应识别方法;然后以一个开口断面风洞试验为背景对本文方法进行验证,并对该断面所受气动效应特性进行研究;最后给出了气动效应的相应研究结论.
1 气动效应识别方法对于桥梁断面而言,风致气动效应往往引起结构振动频率和系统阻尼特性的改变,因此本文较为关注气动效应的两个方面:气动刚度效应和气动阻尼效应.
1.1 气动刚度识别涡激振动具有自限幅振动特性,运动过程中系统振幅、相位等会随时间变化,因此需要对系统瞬时特性进行识别.由于气动刚度的作用,运动过程中的系统振动频率实时变化,因此,需对系统瞬时振动频率进行识别.
瞬时振动频率的概念以往更多用于具有解析形式的单组分 (窄带) 振动信号.对于一个单组分振动系统,其振动位移时程为x(t),对x(t) 进行希尔伯特变换可得到其希尔伯特变换对
| $ \tilde x\left( t \right) = \frac{1}{\pi }P\int_{ - \infty }^\infty {\frac{{x\left( \tau \right)}}{{t - \tau }}{\rm{d}}\tau } . $ | (1) |
其中P为柯西主值.
利用x(t) 和
| $ \omega \left( t \right)=\frac{x\left( t \right)\dot{\tilde{x}}\left( t \right)-\dot{x}\left( t \right)\tilde{x}\left( t \right)}{{{A}^{2}}\left( t \right)}. $ | (2) |
其中A(t) 为位移x(t) 的包络 (即瞬时振幅),
基于希尔伯特变换的系统辨识理论以及上述瞬时频率计算公式的推导过程可参见文献[11-13],关于这部分研究的文献较为详实,本文不再赘述.
上述方法虽具有理论意义,但是用于处理实际试验数据时对数据本身要求极其严格,识别结果容易受到某些局部极值影响,文献[14-15]曾对此进行过详细的分析.为了克服上述困难,文献[15]提出了用于瞬时特性计算的DQ方法 (directly compute quadrature method),并在其论文中对DQ方法、传统HHT方法、以及其他常用方法进行了详细比较,并验证了DQ方法相较传统HHT方法的优势.因此,在本文涡振系统瞬时特性研究中,系统特性识别采用文献[15]提出的DQ方法.
由于瞬时频率的概念建立在窄带振动信号基础上,一般需首先对系统振动位移进行EMD (empirical mode decomposition) 分解,将其分解为若干单组分固有模态函数 (intrinsic mode function, IMF).将系统振动位移进行EMD分解后,得到的单组分IMF可表示为
| $ {{F}_{i}}\left( t \right)={{A}_{i}}\left( t \right)\cdot \cos {{\varphi }_{i}}\left( t \right). $ | (3) |
其中:Ai(t) 为第i个单组分成分Fi(t) 的包络项 (envelope);φi(t) 为瞬时相位;cos φi(t) 为Fi(t) 的振动承载项 (carrier).
瞬时相位φi(t) 关于时间t的导数,即瞬时频率为
| $ {{\omega }_{i}}\left( t \right)=\frac{\text{d}{{\varphi }_{i}}\left( t \right)}{\text{d}t}. $ | (4) |
采用Huang的方法计算瞬时频率时,需首先将Ai(t) 项和cosφi(t) 进行分离,具体分离步骤如下.
步骤1 将Fi(t) 取绝对值得到|Fi(t)|;
步骤2 获取|Fi(t)|的所有局部最大值,形成一个离散序列Lmax(k);
步骤3 用3次样条曲线插值上述局部最大值点离散序列Lmax(k),得到Fi(t) 的第1次经验包络线e1(t);
步骤4 利用e1(t) 对Fi(t) 进行第一次正则化处理:
| $ {{N}_{1}}\left( t \right)=\frac{{{F}_{i}}\left( t \right)}{{{e}_{1}}\left( t \right)}; $ | (5) |
步骤5理想情况下对Fi(t) 进行正则化处理后N1(t) 的值应该全部小于等于1,然而由于在某些局部位置样条曲线可能无法完全穿过所有离散点Lmax(k),因此需要N1(t) 基础上重复步骤4,即
| $ \left\{ \begin{matrix} {{N}_{2}}\left( t \right)=\frac{{{N}_{1}}\left( t \right)}{{{e}_{2}}\left( t \right)}, \\ {{N}_{3}}\left( t \right)=\frac{{{N}_{2}}\left( t \right)}{{{e}_{3}}\left( t \right)}, \\ \vdots \\ {{N}_{n}}\left( t \right)=\frac{{{N}_{n-1}}\left( t \right)}{{{e}_{n}}\left( t \right)}. \\ \end{matrix} \right. $ | (6) |
经过上述步骤后,即可分别得到cosφi(t)、Ai(t) 分别为
| $ \left\{ \begin{array}{l} \cos {\varphi _i}\left( t \right) = {N_n}\left( t \right),\\ {A_i}\left( t \right) = {e_1}\left( t \right){e_2}\left( t \right) \cdots {e_n}\left( t \right). \end{array} \right. $ | (7) |
实现上述计算步骤的前提条件是窄带信号Fi(t) 关于零轴对称 (零均值),并且振动信号的第1个点为某一周期的最大点 (即满足cos函数样式),上述前提条件在实际试验数据处理过程中可轻松实现.
获得窄带信号Fi(t) 包络项Ai(t) 和振动承载项cosφi(t) 后,瞬时相位的计算公式为
| $ {\varphi _i}\left( t \right) = \arctan \frac{{\sqrt {1 - N_n^2\left( t \right)} }}{{{N_n}\left( t \right)}}. $ | (8) |
根据式 (4) 对瞬时相位关于时间t求导,即得到瞬时频率ωi(t).根据包络项Ai(t) 和瞬时频率ωi(t) 的一一对应关系,可得到随瞬时振幅变化的瞬时频率ωi(A).上述刚度项是涡振系统总体刚度效应,气动刚度需在此基础上减去模型在无风情况下得到的悬挂系统本身刚度,具体将在第2部分讨论.
1.2 气动阻尼识别涡激共振过程中,作用于结构表面的气动力与结构运动状态有关.结构周边流场对结构的影响主要体现在附加气动阻尼上.当把结构和周边流场看作一个统一的动力系统时,系统总体阻尼特性中即包含悬挂体系机械阻尼影响又包含了结构所受附加气动阻尼的影响.
为了获得系统总体阻尼特性,需要用到系统“衰减-共振”或“增长-共振”瞬变段位移时程.以“衰减-共振”为例,对结构施加一个大于稳定涡振振幅的初始激励后,结构运动会自起始状态出发逐渐衰减至稳定振动状态,此时的瞬变段类似于自由振动衰减过程,结构振幅可以表示为
| $ {A_i}\left( t \right) = {A_{i0}}\exp \left( { - {\xi _i}{\omega _{ni}}t} \right). $ | (9) |
其中Ai0为某一初始振幅,ωni为系统特征频率,ωni与系统实际振动频率ωi之间满足
| $ {\omega _i} = {\omega _{ni}}\sqrt {1 - \xi _i^2} . $ | (10) |
对式 (9) 两边取对数可得
| $ \ln {A_i}\left( t \right) = - {\xi _i}{\omega _{ni}}t + \ln {A_{i0}}. $ | (11) |
结合式 (10) 可得
| $ \left\{ \begin{array}{l} {\xi _i} = \frac{{\ln \left( {\frac{{{A_{i0}}}}{{{A_i}}}} \right)}}{{{\omega _{ni}}t}},\\ {\omega _{ni}} = \frac{{{\omega _i}}}{{\sqrt {1 - \xi _i^2} }}. \end{array} \right. $ | (12) |
对式 (12) 关于ξi求解,可得到瞬时阻尼比为
| $ {\xi _i}\left( t \right) = \frac{{\ln \left( {\frac{{{A_{i0}}}}{{{A_i}}}} \right)}}{{\left( {{\omega _i} \cdot t} \right)\sqrt {1 + {{\left[ {\frac{{\ln \left( {\frac{{{A_{i0}}}}{{{A_i}}}} \right)}}{{{\omega _i} \cdot t}}} \right]}^2}} }}. $ | (13) |
同样,根据瞬时阻尼比和瞬时振幅的对应关系,可得到随振幅变化的系统总体阻尼比ξi(A).上述系统总体阻尼中包含了悬挂体系机械阻尼和结构所受附加气动阻尼两部分的影响,因此附加气动阻尼效应识别需在总体阻尼比中扣除无风情况下得到的悬挂体系机械阻尼的影响.
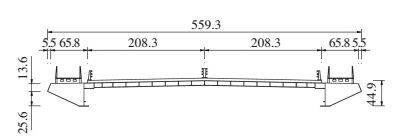
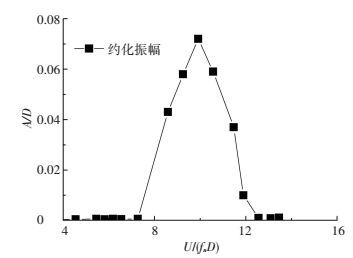
2 开口断面气动效应特性为验证上述气动效应识别方法用于实际桥梁断面涡振研究的可行性,采用某一实际桥梁断面风洞试验数据为背景来进行研究.试验对象为某一开口断面斜拉桥,模型高44.9 mm,宽559.3 mm,长1 740 mm,单位长度模型质量为10.46 kg/m,竖向振动频率为3.37 Hz, 阻尼比为0.4%.试验在同济大学TJ-2号风洞展开,模型断面尺寸及形状如图 1所示,试验获得的节段模型涡振特性如图 2所示.
|
图 1 开口断面形状 (mm) Figure 1 Configuration of the open-section bridge deck (mm) |
|
图 2 涡振响应约化振幅 Figure 2 Reduced amplitudes of VIV |
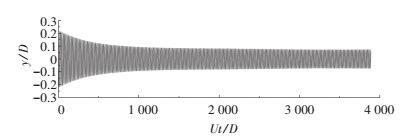
若要获得系统气动效应随振幅的变化规律,需利用试验测得的“衰减-共振”或“增长-共振”位移时程进行系统特性识别.考虑到“衰减-共振”位移时程能覆盖较大的振幅范围,本文开口断面气动效应识别采用试验获得的“衰减-共振”位移时程.锁定区某一风速条件下得到的“衰减-共振”位移时程如图 3所示,图中振幅和时间为无量纲形式.
|
图 3 模型“衰减-共振”位移时程 Figure 3 "Decay-to-resonance" displacement of the cross-sectional model during VIV |
首先对试验获得的模型“衰减-共振”位移时程进行EMD分解以获得窄带的固有模态函数 (IMFs);然后利用上一节涡振系统瞬时特性识别方法获取系统总体阻尼及总体刚度随约化振幅的变化规律.对模型“衰减-共振”位移进行EMD分解后可获得不同频率的IMFs.对于一个试验信号而言,引入EMD分解的目的是将其分解为不同的窄带信号,然后对各窄带信号的频率特性进行识别.由于节段模型涡振位移时程本身即为窄带信号,对其进行EMD分解后仅能获得一个主导IMF,因此,系统特性识别时采用该主导IMF进行.此主导IMF相当于在原始位移信号的基础上进行了时域滤波.
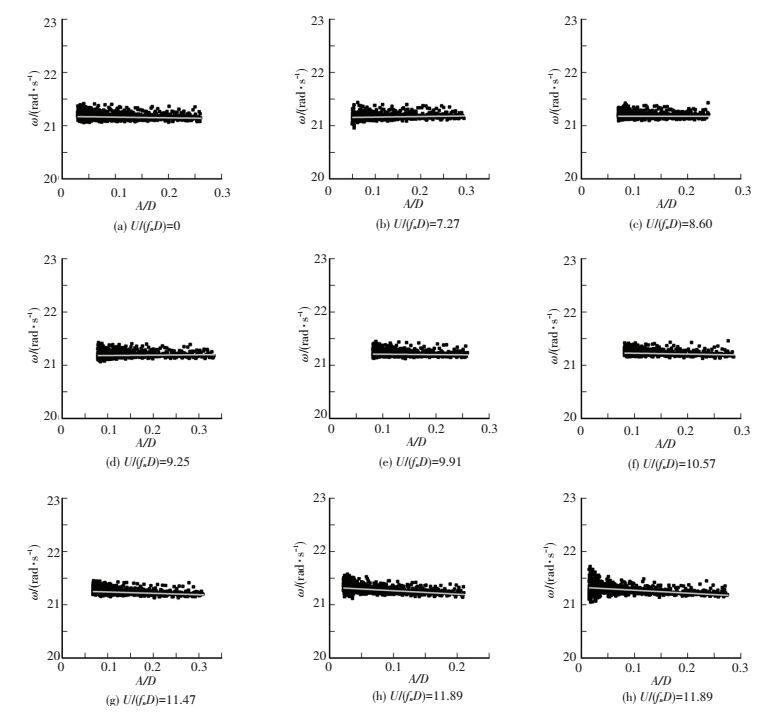
2.1 涡振系统刚度特性基于上述主导IMF按照1.1节瞬时频率识别方法进行计算,可得到不同风速条件下涡振系统瞬时振动频率随结构约化振幅的变化规律,如图 4所示.其中U/(fnD)=0表示弹性悬挂体系在无风情况时的振动频率.图中实心矩形为根据试验数据识别得到的系统瞬时频率成分,实线为四次多项式拟合结果.
|
图 4 不同风速条件下系统振动频率随约化振幅的变化规律 Figure 4 Vibration frequencies of the VIV system versus reduced amplitudes under different wind velocities |
从图 4可以看到:不同约化风速条件下系统振动频率之间的差别相对系统振动频率而言十分微小.同一约化风速条件下,系统振动频率并不随系统振幅的改变而变化,可以认为:涡振系统振动频率不随系统振幅变化,即某一风速条件下流场对结构的附加刚度效应可看作常数.零风速 (U/(fnD)=0) 条件下的结果表明,悬挂系统本身振动频率也不随系统振幅的改变而变化,这说明试验过程中节段模型的悬挂弹簧始终处于弹性工作范围.
2.2 涡振系统阻尼特性获得锁定区不同风速条件下涡振系统瞬时振动频率后,可按照第1.2节计算方法对不同风速条件下涡振系统瞬时阻尼特性进行识别.
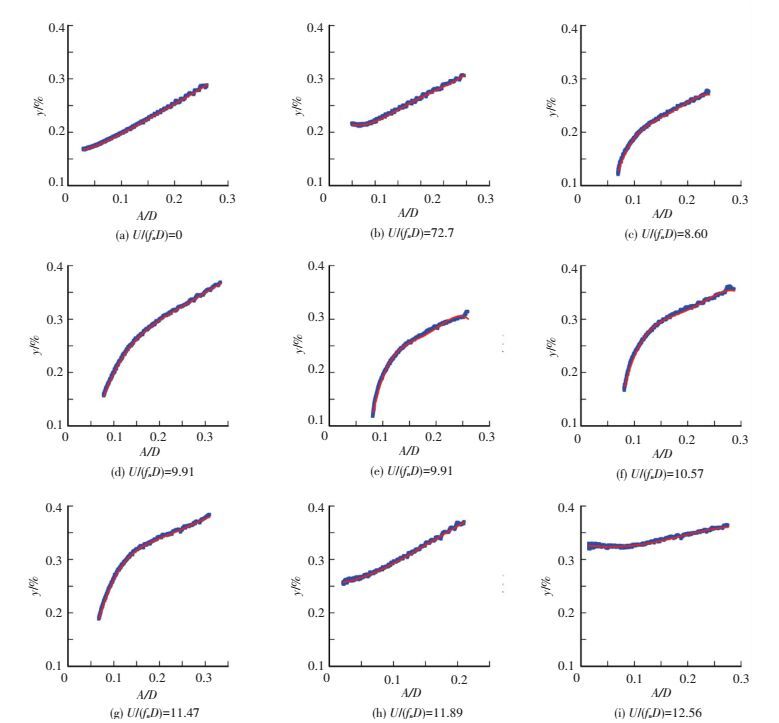
图 5给出了不同风速条件下涡振系统总体阻尼比随约化振幅的变化规律,图中实心矩形为根据试验数据识别的阻尼比,实线为四次多项式拟合结果.
|
图 5 不同风速条件下系统总体阻尼比随约化振幅的变化规律 Figure 5 Total damping ratios of the VIV system versus reduced amplitudes under different wind velocities |
图 5表明:不同约化风速条件下涡振系统总体阻尼比随约化振幅的变化规律并不一致.在锁定区外 (U/(fnD)=7.27和U/(fnD)=12.56),系统总体阻尼比随振幅的变化规律与零风速条件下总体阻尼比变化规律较为接近,呈现“下凹”形,即当结构振幅变小时系统总体阻尼比随振幅的变化规律也变得较为“缓和”,在较小的约化振幅条件下系统总体阻尼比更接近于常数.
锁定区内 (U/(fnD)=8.6~11.89),系统总体阻尼比随约化振幅的变化规律呈现“上凸”形,即随着约化振幅的减小,系统总体阻尼比迅速变小,锁定区内系统总体阻尼比随约化振幅的变化规律与锁定区外或零风速条件下的变化规律明显不同.
固定风速条件下系统总体阻尼比随约化振幅的变化规律呈现明显非线性特性,这表明涡振系统总体阻尼比同时与系统约化风速及约化振幅相关,系统总体阻尼比为约化振幅和约化风速的二元函数.
值得注意的是,零风速条件下弹性悬挂系统本身阻尼比也与系统约化振幅相关.这是由于弹性悬挂体系的阻尼主要由悬挂弹簧相邻线圈间摩擦耗能提供,而不同振幅条件下弹簧相邻线圈间运动周期内的摩擦耗能并不相等,因此即使弹簧处于弹性工作范围,不同振幅条件下的系统机械阻尼比也并不一致.
由于零风速条件下弹性悬挂体系本身阻尼比与约化振幅有关,并不是一个常数,因此在识别涡振系统气动阻尼效应时必须扣除这部分悬挂系统本身阻尼效应带来的影响.传统基于系统自限幅振动位移识别经验模型参数的过程中并未考虑这部分影响,而是假设其阻尼比为常值,这也是导致传统经验模型无法准确模拟附加气动阻尼随结构振幅变化规律的因素之一.
根据不同风速条件下识别获得的系统总体阻尼比随约化振幅的变化规律,可得到总体阻尼比在不同约化风速和约化振幅条件下的等高线图.系统总体阻尼比等高线图可用来直观地反映涡振锁定区内外系统总体阻尼比的变化趋势.
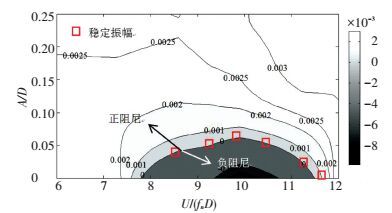
图 6给出了开口断面涡振系统总体阻尼比等高线图.图中等高线的值采用图 5中的四次多项式拟合值.由于试验过程中锁定区风速间距较大,相邻风速间距间的总体阻尼比等高线值通过插值获得.
|
图 6 系统总体阻尼比等高线图 Figure 6 Contour of the total damping ratio of the VIV system |
从图中可以看到:在某些约化振幅和约化风速范围内系统总体阻尼比为负值 (图中深色区域).由于系统总体阻尼比为负,处于该区域的涡振系统是不稳定的,系统振幅会逐渐增加,此时系统总体阻尼比会沿着纵轴向浅色区域发展,当发展至总体阻尼比为零的等高线处附近时,系统将趋于稳定,即稳定振动状态.
而在深色区域外的其他区域,系统总体阻尼比为正值,当系统处于这些区域时,振动系统会逐渐发展至静止状态 (锁定区风速范围以外) 或发展至稳定振动状态 (锁定区风速范围以内).
当涡振系统处于稳定周期振动状态时,系统总体阻尼比为零.图 6中红色矩形为开口断面在不同约化风速条件下测得的稳定振动幅值.从图中可以看到:红色矩形的分布位置与系统总体阻尼比为零的等高线能很好契合,这也进一步验证了本文系统特性识别方法的准确性.
2.3 附加气动效应利用图 5中四次多项式拟合曲线,在不同约化风速条件下,用系统总体阻尼比曲线减去零风速条件下弹性悬挂系统本身阻尼比曲线,即得到涡振发生时系统气动阻尼比随系统约化振幅的变化规律.
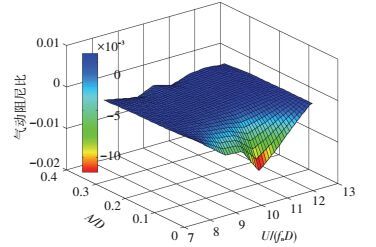
得到的开口断面涡振系统气动阻尼比如图 7所示.可以看到:在锁定区域内 (曲面下凹区域),气动阻尼随约化振幅和约化风速的变化规律呈现明显非线性特性,且气动阻尼值为负值,这是导致结构在该区域内出现涡激振动的原因.而在锁定区域外,气动阻尼比随约化振幅和约化风速的变化较为平缓,这些区域内的气动阻尼值更接近于常数,即线性气动阻尼效应.
|
图 7 开口断面涡振气动阻尼比 Figure 7 Aeroelastic damping ratio of the open-section bridge deck during VIV |
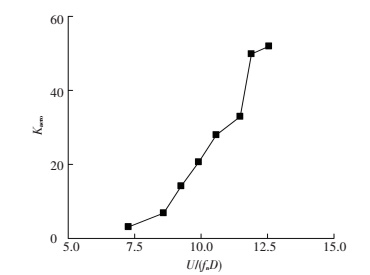
根据图 4结果,涡振系统振动频率可看作只与约化风速有关,与振幅无关.因此各约化风速条件下的气动刚度为常数.图 8给出了不同约化风速条件下的气动刚度值,其中气动刚度定义为
| $ {K_{{\rm{aero}}}} = m\left( {{\omega ^2} - \omega _0^2} \right). $ | (14) |
式中:m为模型质量;ω为涡振系统振动的圆频率 (有风条件);ω0为弹性悬挂体系振动的圆频率 (无风条件).
图 8表明:不同约化风速条件下模型所受气动刚度效应并不相等,锁定区后半段模型所受气动刚度效应大于锁定区前半段模型所受气动刚度效应.不同约化风速条件下模型所受气动刚度效应的不同, 表明跨越锁定区时气动力与结构运动位移间的相位差发生了明显变化.
|
图 8 开口断面涡振气动刚度 Figure 8 Aeroelastic stiffness of the open-section bridge deck during VIV |
1) 识别得到的系统总体阻尼比为零的等高线与试验测得的结构涡振响应曲线能很好吻合,从而验证了系统瞬时特性识别方法的准确性.
2) 利用开口断面试验数据得到的涡振系统附加气动效应结果表明:气动阻尼随结构振幅呈明显非线性变化规律,且各风速下气动阻尼随结构振幅的变化规律并不一致,表明气动阻尼与约化风速和结构振幅同时相关,而各风速下的气动刚度随结构振幅的变化规律则呈线性特性,表明气动刚度可仅看作与约化风速相关而与结构振幅无关.
3) 后续研究可尝试利用某一数学模型对所得到的附加气动效应随结构振幅的变化规律进行模拟,用以计算不同结构参数下的涡振响应.
| [1] | LI H, LAIMA S, OU J, et al. Investigation of vortex-induced vibration of a suspension bridge with two separated steel box girders based on field measurements[J]. Engineering Structures, 2011, 33(6): 1894-1907. DOI: 10.1016/j.engstruct.2011.02.017 |
| [2] | FUJINO Y, YOSHIDA Y. Wind-induced vibration and control of Trans-Tokyo Bay Crossing Bridge[J]. Journal of Structural Engineering, 2002, 128(8): 1012-1025. DOI: 10.1061/(ASCE)0733-9445(2002)128:8(1012) |
| [3] | LARSEN A, ESDAHL S, ANDERSEN J E, et al. Storebælt suspension bridge-vortex shedding excitation and mitigation by guide vanes[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2000, 88(2/3): 283-296. |
| [4] |
张文明, 葛耀君, 杨詠昕, 等. 带挑臂箱梁涡振气动控制试验[J].
哈尔滨工业大学学报, 2010, 42(12): 1948-1952.
ZHANG Wenming, GE Yaojun, YANG Yongxin, et al. Experimental study on aerodynamic control of the vortex induced vibrations of a box girder with projecting slab[J]. Journal of Harbin Institute of Technology, 2010, 42(12): 1948-1952. DOI: 10.11918/j.issn.0367-6234.2010.12.021 |
| [5] |
董锐, 杨詠昕, 葛耀君. 斜拉桥Π型开口断面主梁气动选型风洞试验[J].
哈尔滨工业大学学报, 2012, 44(10): 109-114.
DONG Rui, YANG Yongxin, GE Yaojun. Wind tunnel test for aerodynamic selection of Π shaped deck of cable-stayed bridge[J]. Journal of Harbin Institute of Technology, 2012, 44(10): 109-114. DOI: 10.11918/j.issn.0367-6234.2012.10.023 |
| [6] | EHSAN F, SCANLAN R H. Vortex-induced vibrations of flexible bridges[J]. Journal of Engineering Mechanics-Asce, 1990, 116(6): 1392-1411. DOI: 10.1061/(ASCE)0733-9399(1990)116:6(1392) |
| [7] | GOSWAMI I, SCANLAN R H, JONES N P. Vortex-induced vibration of circular-cylinders: II new model[J]. Journal of Engineering Mechanics-Asce, 1993, 119(11): 2288-2302. DOI: 10.1061/(ASCE)0733-9399(1993)119:11(2288) |
| [8] | SCANLAN R H. Bridge flutter derivatives at vortex lock-in[J]. Journal of Structural Engineering, 1998, 124(4): 450-458. DOI: 10.1061/(ASCE)0733-9445(1998)124:4(450) |
| [9] | LARSEN A. A generalized model for assessment of vortex-induced vibrations of flexible structures[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 57(2): 281-294. |
| [10] | D'ASDIA P, SEPE V, CARACOGLIA L, et al. A model for vortex-shedding induced oscillations of long-span bridges[C]//Proceedings of the 2nd International Structural Engineering and Construction Conference (ISEC-02). Rome: CRC Press, 2003: 2331-2336. |
| [11] | FELDMAN M. Non-linear free vibration identification via the hilbert transform[J]. Journal of Sound and Vibration, 1997, 208(3): 475-489. DOI: 10.1006/jsvi.1997.1182 |
| [12] | FELDMAN M, BUCHER I, ROTBERG J. Experimental identification of nonlinearities under free and forced vibration using the hilbert transform[J]. Journal of Vibration & Control, 2009, 15(10): 1563-1579. |
| [13] | HUANG N E, WU Z. A review on Hilbert-Huang transform: method and its applications to geophysical studies[J]. Reviews of Geophysics, 2008, 46(2): 2008. |
| [14] | NUTTALL A H, BEDROSIAN E. On the quadrature approximation to the Hilbert transform of modulated signals[J]. Proceedings of the IEEE, 1966, 54(10): 1458-1459. DOI: 10.1109/PROC.1966.5138 |
| [15] | HUANG N E, WU Z, LONG S R, et al. On instantaneous frequency[J]. Advances in Adaptive Data Analysis, 2009, 1(2): 177-229. DOI: 10.1142/S1793536909000096 |
 2017, Vol. 49
2017, Vol. 49


