风工程中,建筑结构不但要承受过去某一段时间的风速,还要保证在某一规定的时间期限内安全可靠地承受可能经受的风速.自然界中的风速具有随机性,不同时间有不同的规律,因此有必要根据数理统计的方法来求出建筑结构的设计风速,尤其是对一些重要的对风敏感的结构,如输电塔、桥梁、桅杆等[1-3].大多数荷载规范只能较好地用于建筑结构的风荷载静力分析或是拟静力分析,所以,估算工程场地处重现期内的极值风速是工程抗风设计的首要任务.当以某种极值分布概型拟合风速母样的极值渐近分布时,对重现期内极值风速的估算结果往往与拟合概型和抽样数量有关,桥梁设计规范中规定极值风速分布服从极值-Ⅰ型[4].
目前进行极值-Ⅰ型分布风速预测的方法主要有最大似然估计法、矩估计法和概率权矩法,这3种估计方法均属于经典统计范畴.在对极值-Ⅰ型分布风速预测时,采用矩估计法获得的极值风速偏保守,概率权矩法偏危险,最大似然估计法虽然较前两种方法的精度高,但是公式复杂[5].此外,经典统计有3个共同的局限性:一是提高统计推断的精度,主要靠数据多少决定,这对于小样本,往往发生很大困难甚至无能为力;二是在对极值-Ⅰ型风速预测的过程中均假定位置参数和尺度参数是各自独立的参数,而在理论上的极值-Ⅰ型分布模型中,位置参数和尺度参数不是相互独立的;三是仅仅依靠样本信息对参数进行估计,而没有依靠模型的先验信息.因此,前述的最大似然估计法、矩估计法和概率权矩法在对极值-Ⅰ型分布风速进行预测时的精度就受到了限制.为了弥补现有极值-Ⅰ型风速预测方法的不足,本文采用Bayes统计理论[6]建立了极值-Ⅰ型风速预测方法.该方法有以下特点:1) Bayes统计理论利用样本信息对先验信息进行修正而得到后验信息;2) Bayes统计由于利用了模型的先验信息,因而对于小样本一般也有较好的统计推断效果;3) Bayes统计对于极值-Ⅰ型模型中的位置参数和尺度参数是否相互独立均适用.最后,通过算例验证了该方法的准确性与有效性.
1 基于Bayes理论的极值-Ⅰ型风速预测方法 1.1 极值-Ⅰ型分布| $ f\left( t \right) = \frac{1}{\sigma }\exp \left[ { - \frac{{t - \mu }}{\sigma } - \exp \left( { - \frac{{t - \mu }}{\sigma }} \right)} \right], $ | (1) |
| $ F\left( t \right) = \exp \left\{ { - \exp \left[ { - \left( {\frac{{t - \mu }}{\sigma }} \right)} \right]} \right\}. $ | (2) |
式中μ、σ分别为位置参数和尺度参数.
对 (2) 式两边取对数,得到重现期为T(保证率为1-
| $ {t_{\frac{1}{T}}} = \mu - \sigma \ln \left[ { - \ln \left( {1 - \frac{1}{T}} \right)} \right]. $ | (3) |
从而,得到百年一遇的风速预测值t0.01为
| $ {t_{0.01}} = \mu - \sigma \ln \left[ { - \ln 0.99} \right] = \mu + 4.6\sigma . $ | (4) |
采用Bayes理论将μ和σ作为随机变量来估计μ和σ的联合概率密度函数π(μ, σ),下面采用Jeffreys无信息先验分布来对t
Jeffreys用Fisher信息矩阵行列式的平方根作为 (μ, σ) 先验密度的核,用Jeffreys准则寻找无信息先验分布[6, 9]的步骤如下.
步骤1 写出样本似然函数的对数:
| $ \begin{array}{l} L = \ln \left[ {L\left( {t\left| {\mu ,\sigma } \right.} \right)} \right] = \ln \left[ {\prod\limits_{i = 1}^n {f\left( {{t_i}\left| {\mu ,\sigma } \right.} \right)} } \right] = \\ \;\;\;\;\;\;\;\sum\limits_{i = 1}^n {\ln f\left( {{t_i}\left| {\mu ,\sigma } \right.} \right)} . \end{array} $ | (5) |
步骤2 求Fisher信息矩阵:
| $ \mathit{\boldsymbol{I}}\left( {\mu ,\sigma } \right) = E\left( { - \frac{{{\partial ^2}L}}{{\partial \mu \partial \sigma }}} \right). $ | (6) |
步骤3 求 (μ, σ) 的无信息先验密度函数:
| $ \pi \left( {\mu ,\sigma } \right) = {\left[ {\det \mathit{\boldsymbol{I}}\left( {\mu ,\sigma } \right)} \right]^{\frac{1}{2}}}. $ | (7) |
对于极值-Ⅰ型分布,Fisher信息矩阵为
| $ \mathit{\boldsymbol{I}}\left( {\mu ,\sigma } \right) = - E\left| {\begin{array}{*{20}{c}} {\frac{{{\partial ^2}\ln L}}{{\partial {\mu ^2}}}} & {\frac{{{\partial ^2}\ln L}}{{\partial \mu \partial \sigma }}}\\ {\frac{{{\partial ^2}\ln L}}{{\partial \mu \partial \sigma }}} & {\frac{{{\partial ^2}\ln L}}{{\partial {\sigma ^2}}}} \end{array}} \right|. $ | (8) |
由Jeffreys准则可得
| $ \pi \left( {\mu ,\sigma } \right) = \frac{1}{{{\sigma ^2}}}. $ | (9) |
下面基于π(μ, σ),采用Lindley近似[9-11]方法推导t
| $ I = \frac{{\int {u\left( \theta \right)v\left( \theta \right){{\rm{e}}^{L\left( \theta \right)}}{\rm{d}}\theta } }}{{\int {v\left( \theta \right){{\rm{e}}^{L\left( \theta \right)}}{\rm{d}}\theta } }}. $ | (10) |
其中θ=(θ1, θ2, …, θk) 为参数向量,L为似然函数的对数.需要注意的是,I为在给定先验分布v(θ) 的情况下u(θ) 的后验期望.
根据Lindley近似方法,由式 (10) 可得
| $ \begin{array}{*{20}{c}} {\;{u_1} = \frac{{\partial u}}{{\partial {\theta _1}}},\;\;\;\;{u_2} = \frac{{\partial u}}{{\partial {\theta _2}}};}\\ {{u_{11}} = \frac{{{\partial ^2}u}}{{\partial \theta _1^2}},\;\;\;\;{u_{22}} = \frac{{{\partial ^2}u}}{{\partial \theta _2^2}};}\\ {p = \pi \left( {{\theta _1},{\theta _2}} \right);}\\ {\;{p_1} = \frac{{\partial p}}{{\partial {\theta _1}}},\;\;\;\;{p_2} = \frac{{\partial p}}{{\partial {\theta _2}}};}\\ {{L_{20}} = \frac{{{\partial ^2}L}}{{\partial \theta _1^2}},\;\;\;\;{L_{02}} = \frac{{{\partial ^2}L}}{{\partial \theta _2^2}};}\\ {{L_{30}} = \frac{{{\partial ^3}L}}{{\partial \theta _1^3}},\;\;\;\;{L_{03}} = \frac{{{\partial ^3}L}}{{\partial \theta _2^3}};}\\ {{\sigma _{11}} = {{\left( { - {L_{20}}} \right)}^{ - 1}},\;\;\;\;{\sigma _{22}} = {{\left( { - {L_{02}}} \right)}^{ - 1}}.} \end{array} $ |
进一步可得
| $ \begin{array}{l} E\left( {u\left( \theta \right)\left| {\overrightarrow t } \right.} \right) = u\left( {\overline {{\theta _1}} ,\overline {{\theta _2}} } \right) + \frac{1}{2}\left( {{u_{11}}{\sigma _{11}} + {u_{22}}{\sigma _{22}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{p_1}{u_1}{\sigma _{11}} + {p_2}{u_2}{\sigma _{22}} + \frac{1}{2}\left( {{L_{30}}{u_1}\sigma _{11}^2 + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{L_{03}}{u_2}\sigma _{22}^2 + {L_{21}}{u_2}{\sigma _{11}}{\sigma _{22}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{L_{12}}{u_1}{\sigma _{22}}{\sigma _{11}}} \right). \end{array} $ | (11) |
其中
极值-Ⅰ型风速预测表达式为
| $ {t_B} = \mu - b\sigma = u\left( {\mu ,\sigma } \right). $ | (12) |
式中μ=θ1,σ=θ2.由此可得u1=1,u2=-b,其中b=ln (-ln
| $ \begin{array}{*{20}{c}} {p\left( {{\theta _1},{\theta _2}} \right) = \pi \left( {\mu ,\sigma } \right) = \frac{1}{{{\sigma ^2}}},}\\ {{p_1} = 0,{p_2} = - \frac{2}{{{\sigma ^3}}}.} \end{array} $ |
令μ、σ分别为μ、σ的最大似然估计值,可得
| $ \ln L = - n\ln \sigma - \sum\limits_{i = 1}^n {\frac{{{t_i} - \mu }}{\sigma }} - \sum\limits_{i = 1}^n {{{\rm{e}}^{ - \frac{{{t_i} - \mu }}{\sigma }}}} . $ | (13) |
所以
| $ \begin{array}{l} \frac{{\partial \ln L}}{{\partial \mu }} = \frac{n}{\sigma } - \frac{1}{\sigma }\sum\limits_{i = 1}^n {{{\rm{e}}^{ - \frac{{{t_i} - \mu }}{\sigma }}}} ,\\ {L_{20}} = \frac{{{\partial ^2}\ln L}}{{\partial {\mu ^2}}} = - \frac{1}{{{\sigma ^2}}}\sum\limits_{i = 1}^n {{{\rm{e}}^{ - \frac{{{t_i} - \mu }}{\sigma }}}} ,\\ \frac{{\partial \ln L}}{{\partial \sigma }} = \frac{n}{\sigma } + \sum\limits_{i = 1}^n {\frac{{{t_i} - \mu }}{{{\sigma ^2}}}} - \frac{1}{{{\sigma ^2}}}\sum\limits_{i = 1}^n {{{\rm{e}}^{ - \frac{{{t_i} - \mu }}{\sigma }}}} \left( {{t_i} - \mu } \right),\\ {L_{02}} = \frac{{{\partial ^2}\ln L}}{{\partial {\sigma ^2}}} = \frac{n}{{{\sigma ^2}}} - \left\{ {\sum\limits_{i = 1}^n {2\left( {{t_i} - \mu } \right)\left[ {1 - {{\rm{e}}^{ - \frac{{{t_i} - \mu }}{\sigma }}}} \right]} } \right\}\frac{1}{{{\sigma ^3}}} + \\ \;\;\;\;\;\;\;\;\;\left[ {\sum\limits_{i = 1}^n {{{\rm{e}}^{ - \frac{{{t_i} - \mu }}{\sigma }}}} \left( {{t_i} - \mu } \right)2} \right]\frac{1}{{{\sigma ^4}}},\\ {L_{03}} = \frac{{{\partial ^3}\ln L}}{{\partial {\sigma ^3}}} = \frac{{ - 2n}}{{{\sigma ^3}}} + 6\left\{ {\sum\limits_{i = 1}^n {\left( {{t_i} - \mu } \right)\left[ {1 - {{\rm{e}}^{ - \frac{{{t_i} - \mu }}{\sigma }}}} \right]} } \right\}\frac{1}{{{\sigma ^4}}} + \\ \;\;\;\;\;\;\;\;6\left[ {\sum\limits_{i = 1}^n {{{\rm{e}}^{ - \frac{{{t_i} - \mu }}{\sigma }}}} \left( {{t_i} - \mu } \right)2} \right]\frac{1}{{{\sigma ^5}}} - \left[ {\sum\limits_{i = 1}^n {{{\rm{e}}^{ - \frac{{{t_i} - \mu }}{\sigma }}}} \left( {{t_i} - \mu } \right)3} \right]\frac{1}{{{\sigma ^6}}},\\ {L_{21}} = \frac{\partial }{{\partial \sigma }}\left( {\frac{{{\partial ^2}\ln L}}{{\partial {\mu ^2}}}} \right) = \left[ {\sum\limits_{i = 1}^n {{{\rm{e}}^{ - \frac{{{t_i} - \mu }}{\sigma }}}} } \right]\frac{2}{{{\sigma ^3}}} - \left[ {\sum\limits_{i = 1}^n {{{\rm{e}}^{ - \frac{{{t_i} - \mu }}{\sigma }}}} \left( {{t_i} - \mu } \right)} \right]\frac{1}{{{\sigma ^4}}},\\ {L_{12}} = \frac{\partial }{{\partial \mu }}\left( {\frac{{{\partial ^2}\ln L}}{{\partial {\sigma ^2}}}} \right) = \frac{2}{{{\sigma ^3}}}\left[ {n - \sum\limits_{i = 1}^n {{{\rm{e}}^{ - \frac{{{t_i} - \mu }}{\sigma }}}} } \right] + \\ \;\;\;\;\;\;\;\;\frac{1}{{{\sigma ^4}}}\left[ {\sum\limits_{i = 1}^n {{{\rm{e}}^{ - \frac{{{t_i} - \mu }}{\sigma }}}} \left( {{t_i} - \mu } \right)} \right] - \\ \;\;\;\;\;\;\;\;\frac{1}{{{\sigma ^5}}}\left[ {\sum\limits_{i = 1}^n {{{\left( {{t_i} - \mu } \right)}^2}{{\rm{e}}^{ - \frac{{{t_i} - \mu }}{\sigma }}}} } \right]. \end{array} $ |
因此,可得t
| $ \begin{array}{l} \overline {{t_B}} = \overline {{t_{\frac{1}{T}}}} + {p_2}{\mu _2}{\sigma _{22}} + \frac{1}{2}\left( {{L_{30}}\sigma _{11}^2 + {L_{03}}{u_2}\sigma _{22}^2 + } \right.\\ \;\;\;\;\;\;\left. {{L_{21}}{u_2}{\sigma _{11}}{\sigma _{22}} + {L_{12}}{\mu _1}{\sigma _{22}}{\sigma _{11}}} \right). \end{array} $ | (14) |
从上述Bayes估计理论可得极值-Ⅰ型风速预测值为
| $ \begin{array}{l} \overline {{t_B}} = \bar \mu + 4.6\bar \sigma + {p_2}{\mu _2}{\sigma _{22}} + \frac{1}{2}\left( {{L_{30}}\sigma _{11}^2 + {L_{03}}{u_2}\sigma _{22}^2 + } \right.\\ \;\;\;\;\;\;\left. {{L_{21}}{u_2}{\sigma _{11}}{\sigma _{22}} + {L_{12}}{\mu _1}{\sigma _{22}}{\sigma _{11}}} \right). \end{array} $ | (15) |
式中μ、σ分别为μ和σ的最大似然估计值.
2 数值算例本文调查和收集了安徽安庆宿松县、望江县两个气象站1971—2011年实测的风速资料 (共计744个风速样本),以此提供伪风速母样概率分布模型中位置参数μ和尺度参数σ的合理取值.基于上述伪风速母样概率分布模型参数的合理取值,建立伪风速母样理论模型,然后将Bayes估计和最大似然估计[12-16]的重现期为100 a极值-Ⅰ型风速预测值与理论模型值进行比较分析.
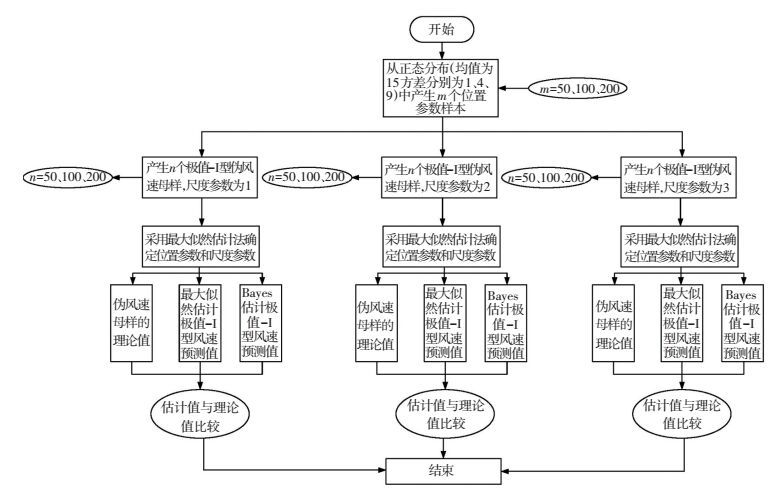
在伪风速母样理论模型的建立过程中,首先,假定伪风速母样概率分布模型中的位置参数μ和尺度参数σ为相互独立的随机变量,位置参数μ服从正态分布,尺度参数σ服从均匀分布[7];其次,考虑样本数量、位置参数μ的先验方差和尺度参数σ的变化对极值-Ⅰ型风速预测结果的影响;最后,基于位置参数μ和尺度参数σ,采用Monte Carlo法产生伪风速母样.本文采用的极值-Ⅰ型风速预测流程如图 1所示.
|
图 1 极值-Ⅰ型风速预测流程 Figure 1 Flow chart of the numerical analysis |
极值-Ⅰ型风速预测结果见表 1~3,其中,μB表示采用m个先验样本计算位置参数的Bayes估计值,而μ和σ分别表示位置参数和尺度参数的最大似然估计值,t
由表 1~3可以看出:1) 当位置参数先验样本数为50,极值-Ⅰ型风速Bayes估计值比最大似然估计值更接近伪风速母样理论值.2) 随着位置参数先验样本数和伪风速母样样本数的增加,尺度参数的增大,极值-Ⅰ型风速Bayes估计值与最大似然估计值之间的差异越来越小.3) 极值-Ⅰ型风速Bayes估计精度随着伪风速母样样本数的增加而提高.4) 位置参数先验样本数量的多少和先验方差的大小对Bayes估计精度没有影响.5) 在大多数情况下,极值-Ⅰ型风速Bayes估计比最大似然估计精度高.
|
表 1 μ~N(15, 1), σ=1, 2, 4, |
|
表 2 μ~N(15, 2), σ=1, 2, 4, |
|
表 3 μ~N(15, 3), σ=1, 2, 4, |
选择安徽安庆市宿松县和望江县气象站作为采样测站,调查和收集了两个气象站1971—2011年原始风速记录共2×372个,包含了1971年1月至2011年12月的全部372个月的月最大风速值.选取31个年最大风速值进行百年一遇极值风速预测,采用本文提出的Bayes估计方法预测的安徽安庆宿松县和望江县的百年一遇最大风速值分别为27.89 m/s和24.20 m/s,为安全起见,取27.89 m/s作为本文贝叶斯理论预测的安徽安庆市百年一遇风速值.该计算结果与《公路桥梁抗风设计规范》[4]附表A规定的安徽安庆市百年一遇风速值27.1 m/s相比误差较小,这表明采用本文提出的贝叶斯方法进行实际工程场地极值风速预测是合理可行的.
4 结论1) 基于Bayes理论提出了极值-Ⅰ型风速预测方法,采用Monte Carlo法产生伪风速母样,分别进行极值-Ⅰ型风速Bayes估计和最大似然估计,并将两者的估计结果与伪风速母样理论值进行比较.
2) 与最大似然估计相比,采用Bayes估计进行极值-Ⅰ型风速预测精度更高.随着极值-Ⅰ型伪风速母样样本数增加,Bayes估计极值-Ⅰ型风速的误差变小.极值-Ⅰ型分布中位置参数的先验样本数和先验方差均不影响Bayes估计极值-Ⅰ型风速预测精度.
3) 在大样本和大尺度参数下,采用Bayes估计极值-Ⅰ型风速预测值与最大似然估计值的差异较小.
| [1] |
黄文锋, 周焕林, 孙建鹏. 应用台风风场经验模型的台风极值风速预测[J].
哈尔滨工业大学学报, 2016, 48(2): 142-146.
HUANG Wenfeng, ZHOU Huanlin, SUN Jianpeng. Prediction typhoon design wind speed with empirical typhoon wind field model[J]. Journal of Harbin Institute of Technology, 2016, 48(2): 142-146. DOI: 10.11918/j.issn.0367-6234.2016.02.024 |
| [2] | COLES S G, TAWN J A. Statistical methods for multivariate extremes: an application to structural design[J]. Applied Statistics, 1994, 43(1): 1-48. DOI: 10.2307/2986112 |
| [3] | ZHAO Lin, KE Shitang, GE Yaojun. Extreme value estimation of non-Gaussian aerodynamic series of cooling tower [C]//6th International Symposium on Cooling Towers. Bensberg: Luikov Institute of Heat and Mass Transfer of National Academy of Sciences of Belarus, 2012: 20-23. |
| [4] |
中交公路规划设计院. 公路桥梁抗风设计规范: JTG/T D60-1—2004 [S]. 北京: 人民交通出版社, 2004.
CCCC Highway Consultants Co., Ltd.. Wind-resistant design specification for highway bridges: JTG/T D60-1—2004 [S]. Beijing: China Communications Press, 2004. |
| [5] |
卢安平, 赵林, 郭增伟, 等. 基于Monte Carlo法的极值分布类型及其参数估计方法比较[J].
哈尔滨工业大学学报, 2013, 45(2): 88-95.
LU Anping, ZHAO Lin, GUO Zengwei, et al. A comparative study of extreme value distribution and parameter estimation based on the Monte Carlo method[J]. Journal of Harbin Institute of Technology, 2013, 45(2): 88-95. DOI: 10.11918/j.issn.0367-6234.2013.02.016 |
| [6] | BERNARDO J M, SMITH F M. Bayesian theory: Wiley series in probability and mathematical statistics: probability and mathematical statistics[M]. Chichester:John Wiley & Sons Ltd., 1994. |
| [7] | KANG M, KO K, HUH J. Determination of extreme wind values using the Gumbel distribution[J]. Energy, 2015, 86: 51-58. DOI: 10.1016/j.energy.2015.03.126 |
| [8] | VIDAL I. A Bayesian analysis of the Gumbel distribution: an application to extreme rainfall data[J]. Stochastic Environmental Research and Risk Assessment, 2014, 28(3): 571-582. DOI: 10.1007/s00477-013-0773-3 |
| [9] | MILADINAVIC B, TSOKOS C P. Ordinary, Bayes, empirical Bayes, and non-parametric reliability analysis for the modifiedGumbel failure model[J]. Nonlinear Analysis, 2009, 71(12): 1426-1436. DOI: 10.1016/j.na.2009.01.181 |
| [10] | GUURE C B, IBRAHIM N A. Approximate Bayesian estimates of Weibull parameters with Lindley's method[J]. Sains Malaysiana, 2014, 43(9): 1433-1437. |
| [11] | ALI S. On the Bayesian estimation of the weighted Lindley distribution[J]. Journal of Statistical Computation and Simulation, 2015, 85(5): 855-880. DOI: 10.1080/00949655.2013.847442 |
| [12] |
葛耀君. 桥梁结构风振可靠性理论及其应用研究[D]. 上海: 同济大学, 1997.
GE Yaojun. Research on the bridge structure wind-induced reliability theory and application [D]. Shanghai: Tongji University, 1997. http://www.oalib.com/references/16917563 |
| [13] |
项海帆, 葛耀君, 朱乐东, 等.
现代桥梁抗风理论与实践[M]. 北京: 人民交通出版社, 2005.
XIANG Haifan, GE Yaojun, ZHU Ledong, et al. Modern theory and practice on bridge wind resistance[M]. Beijing: China Communications Press, 2005. |
| [14] |
陈政清.
工程结构的风致振动、稳定与控制[M]. 北京: 科学出版社, 2013.
CHEN Zhengqing. Wind-induced vibration, stability and control of engineering structure[M]. Beijing: Science Press, 2013. |
| [15] |
葛耀君.
大跨度悬索桥抗风[M]. 北京: 人民交通出版社, 2011.
GE Yaojun. Wind resistance of long span suspension bridges[M]. Beijing: China Communications Press, 2011. |
| [16] |
葛耀君.
大跨度拱式桥抗风[M]. 北京: 人民交通出版社, 2014.
GE Yaojun. Wind resistance of long arch suspension bridges[M]. Beijing: China Communications Press, 2014. |
 2017, Vol. 49
2017, Vol. 49


