2. 上海市政工程设计研究总院 (集团) 有限公司,上海 200092
2. Shanghai Municipal Engineering Design Institute (Group) Co., Ltd., Shanghai 200092, China
斜拉桥混合塔上塔柱用钢结构,索塔锚固区结构简单,受力明确,下塔柱用混凝土结构能够承受较大竖向压应力,中间用钢-混凝土结合部将两者连接在一起形成混合结构体系,结构性能得到大幅度的提高.
近年来混合塔在大跨度斜拉桥中逐渐得到推广应用[1-4].然而钢-混凝土结合部两侧桥塔刚度相差较大,结合部内部构造复杂,材料特性与结构特性的突变容易导致应力集中的现象发生,容易形成结构的薄弱点[5-9],是混合塔设计最为关键的环节.目前,国内外关于混合塔结合部的理论研究较少,结合段的受力和传力机理主要通过模型试验和有限元分析来研究,实桥多采用试验来验证结合部的基本力学性能,验证设计的合理性[10-11].
本文结合在建的某混合塔斜拉桥,对有格室后承压板式结合部进行了模型试验,分析结合部各构件的受力特点、应力分布规律,并结合有限元模型,以结合部长度、承压板厚度、连接件间距和开孔板孔径为变化参数对结合部传力机理进行研究,为钢-混凝土结合部的设计提供参考.
1 混合塔结合部构造特点混合塔结合部由钢塔加劲过渡段和钢-混凝土结合段组成.结合部将钢塔所受的轴力、剪力、弯矩通过钢塔加劲过渡段加以分散,再通过结合部钢格室的承压板、抗剪连接件的过渡段作用传递给格室填充混凝土,进而传递给混凝土塔.
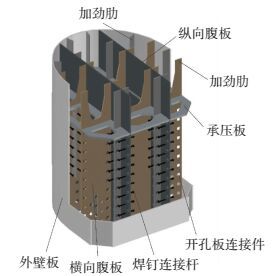
图 1为某斜拉桥混合塔结合部构造示意.结合部高4.7 m,位于索塔锚固区下部,在钢塔加劲过渡段外壁板及两条纵向腹板上设置加劲肋进行刚度过渡.结合部混凝土顶面设置一块厚为60 mm的承压板,两条纵向腹板及加劲板贯穿至结合部中并在加劲肋上开直径75 mm圆孔,并贯穿直径25 mm的钢筋形成开孔板连接件,在格室内钢板上焊接直径22 mm、长度为200 mm焊钉,连接件沿塔竖向间距为200 mm.结合部格室内布置构造钢筋并浇筑混凝土与下部混凝土塔柱结合.
|
图 1 结合部构造 Figure 1 Structure of composite joint |
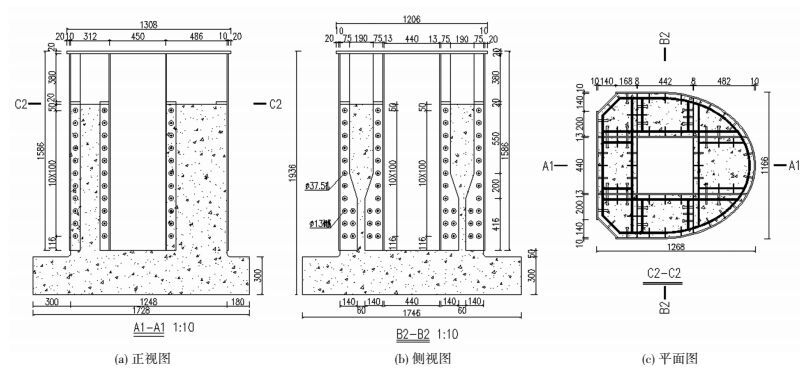
综合考虑加载条件和模型制作,对该桥单肢桥塔结合部进行1:3缩尺模型试验. 图 2为结合部试验模型构造,模型高1 936 mm,截面尺寸为1 766 mm×1 728 mm,顶部焊接20 mm厚的钢板作为加载端,底部浇注300 mm的混凝土底座作为支撑端.
|
图 2 模型构造 (mm) Figure 2 Size of test model (mm) |
试验模型与实桥模型钢构件板厚和荷载的缩尺比分别为1:3和1:9,弹性模量和应力缩尺比为1:1.开孔板和焊钉连接件按照塔竖向线刚度相似原则布置,试验模型截面内连接件数量与实桥布置一致.开孔板孔径为37.5 mm,孔中贯穿直径为13 mm的HRB335钢筋,焊钉直径为13 mm、长度为80 mm.连接件沿塔竖向间距为100 mm.采用等级为C55的混凝土并对其进行材性试验,测得混凝土抗压强度、抗拉强度和弹性模量分别为67.8、3.2 MPa和41.5 GPa.钢板采用Q345qd,钢材和钢筋按照规范进行了试件的制作和测试,钢材实测材性试验结果平均值见表 1.表中板件厚度、屈服强度、抗拉强度和弹性模量分别用t、fy、ft和Ec表示.
| 表 1 钢构件材性试验结果 Table 1 Material properties of steel components |
模型加载如图 3所示,根据全桥有限元模型计算出单肢桥塔结合部最不利轴力为57 167.5 kN,剪力和弯矩相对较小,不考虑剪力和弯矩对结合部的影响.根据相似准则拟定模型设计轴力P为6 500 kN,模型共进行2次往复加载,分别加载到1.0P和2.5P后卸载,加载等级为0.1P.加载前先进行0.3P预加载.

|
图 3 加载及测试装置 Figure 3 Load and test devices |
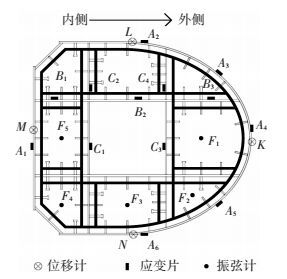
模型测点布置如图 4所示.采用应变片测试格室钢板的应变,外壁板应变片测点沿顺时针方向依次是A1、A2、A3、A4、A5、A6;横向腹板应变片测点依次为C1、C2、C3、C4;纵向腹板应变片测点依次为B1、B2、B3;每列设置7排测点,编号顺序按照从上往下依次为1、2、3、4、5、6、7.
|
图 4 测点平面布置 Figure 4 Layout of measuring points |
在钢格室内设置埋入式应变计,对混凝土内部应变进行测试,应变计测点在横截面上依次为F1、F2、F3、F4,F5从上到下共设置4排,编号依次为1、2、3、4.钢与混凝土间的相对滑移和整体压缩位移均采用千分表测试.测量相对滑移的千分表测点分别为K1、L1、M1、N1,设置在结合部底部;测量整体压缩位移的千分表测点分别为K2、L2、M2、N2,设置在承压板位置处的外壁板上.
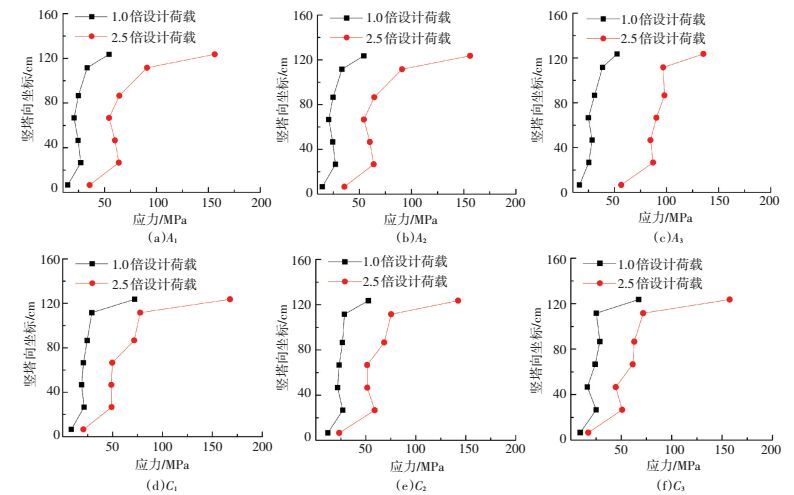
3 试验结果及有限元分析 3.1 钢板应力图 5为1.0P和2.5P轴力作用下钢结构部分测点竖向正应力沿塔竖向分布曲线.随着距承压板距离的增加钢板的竖向应力沿塔竖向呈现出逐渐减小的趋势,在承压板位置区域钢板竖向应力衰减较快,说明承压板承担了部分荷载.承压板以下钢结构竖向应力减少且趋势较为平缓,说明连接件传力较为平顺,传力效果较好. 2.5P作用下实测钢板最大应力为167 MPa,荷载从1.0P提高至2.5P,应力增加值接近150%,表明绝大部分钢板处于弹性工作阶段,钢结构具有较高的安全储备.
|
图 5 钢结构应力分布 Figure 5 Stress distribution of steel structure |
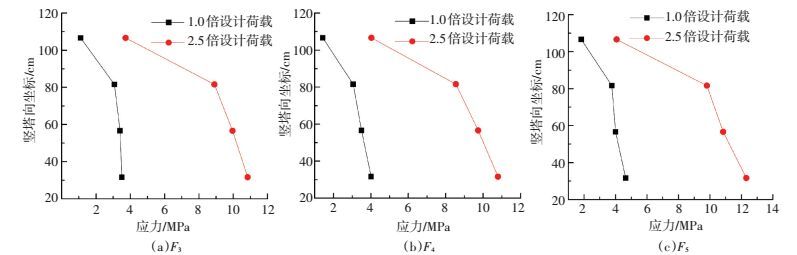
图 6为1.0P和2.5P轴力作用下混凝土结构部分测点竖向正应力沿塔竖向分布曲线.混凝土结构的竖向应力从上往下呈现出逐渐增加的趋势,结合部通过承压板和连接件将钢板上的应力逐步传递给混凝土结构.靠近承压板位置混凝土应力增加较快,距承压板较远的区域混凝土应力增加的趋势逐渐减小. 2.5P作用下实测混凝土最大应力为12.3 MPa,荷载从1.0P提高到2.5P,应力增加值接近150%,表明绝大部分混凝土处于弹性工作阶段.
|
图 6 混凝土结构应力分布 Figure 6 Stress distribution of concrete structure |
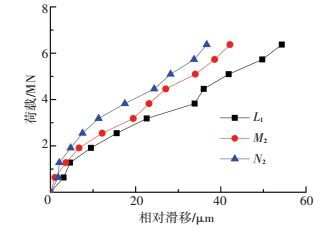
图 7给出了结合部端部钢板与混凝土间的荷载-滑移曲线. 1.0P轴力作用下端部相对滑移数值分别为0.056、0.039、0.039 mm,相对滑移较小,钢结构与混凝土结构变形协调,连接件具有足够的抗剪刚度将荷载传递给混凝土,钢结构与混凝土结构协作性能较好. 2.5P轴力作用下最大滑移量0.196、0.083、0.139 mm,表明连接件具有较高的安全储备.
|
图 7 荷载-滑移曲线 Figure 7 Load-slippage curves |
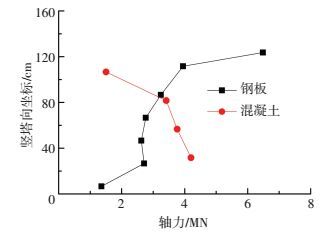
图 8给出了钢结构及混凝土结构承担的荷载轴力沿塔竖向分布,其中轴力为测点相邻区域平均值乘以测点区域面积并求和.由图可知混凝土结构承担的轴力沿塔竖向从上往下逐渐增加,钢板承担的轴力沿塔竖向从上往下逐渐减小,钢板上的力逐渐传递给了混凝土结构.承压板位于钢板第1排测点和第2排测点之间,两排测点位置钢结构分担轴力的差即为承压板所传递的轴力,其数值为2 538 kN,承压板承担了约40%的荷载.
|
图 8 钢板及混凝土承担轴力沿塔竖向分布 Figure 8 Distribution of axial force along the vertical shared by steel and concrete structure |
采用通用有限元软件ANSYS基于试验模型建立的混合塔钢-混凝土结合部混合有限元模型.其中钢结构采用板壳单元SHELL63来模拟,混凝土结构采用实体单元SOLID65来模拟.钢与混凝土结合面之间的接触承压作用采用接触单元模拟,忽略接触面之间的粘结摩擦作用.连接件采用非线性弹簧单元模拟,由推出试验得出的开孔板和焊钉连接件的剪力-滑移非线性本构关系[12-15]分别为
| $\begin{array}{l} V/{V_{\rm{u}}} = \frac{{15.25\left( {s/{s_{\rm{p}}}} \right)}}{{{{\left( {s/{s_p}} \right)}^2} + 13.32\left( {s/{s_{\rm{p}}}} \right) + 1.03}},\\ V/{V_{\rm{u}}} = 1.5{\left( {s/{s_{\rm{p}}}} \right)^{1/3}} - 0.5\left( {s/{s_{\rm{p}}}} \right). \end{array}$ |
式中Vu为连接件抗剪承载力,sp为连接件峰值滑移.模型的边界条件为底座截面的所有节点固结,对加载板施加轴向面荷载.
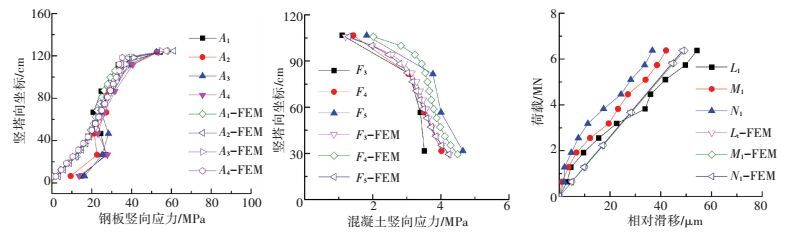
4.2 有限元与试验结果对比图 9给出了计算结果与试验结果的比较曲线.数值模型与试验模型得出的应力及相对滑移分布规律及数值吻合度较高.采用非线性弹簧元对开孔板和焊钉连接件进行数值模拟具有较高的工程精度.
|
图 9 试验与有限元结果的比较 Figure 9 Comparison between FEM and model test |
为研究结合部传力机理,采用非线性弹簧元建立实桥结合部有限元模型.对结合部连接件竖向剪力沿桥塔竖向分布规律进行分析,并通过变化结合部关键参数研究其对结合部连接件受力的影响.
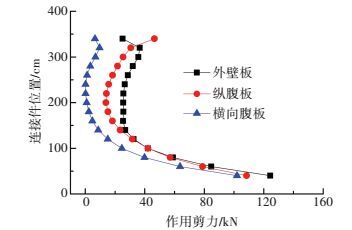
5.1 接件受力分布图 10给出了1.0P轴力作用下外壁板、纵向腹板和横向腹板上开孔板连接件最大竖向剪力沿塔竖向分布.距承压板0.6L (L为结合部长度) 范围内的连接件竖向剪力Vs较小,受承压板约束作用,在距承压板一定范围内钢与混凝土间相对滑移较小,钢结构与混凝土之间的力主要靠承压板传递.距承压板0.6 L~1.0 L之间几排连接件,竖向剪力值Vs逐渐增大,且越靠近结合部底部连接件竖向剪力Vs增加的趋势越大.钢-混凝土结合部底部,钢与混凝土结构的荷载主要靠连接件传递.开孔板连接件最大竖向剪力值为125 kN.
|
图 10 连接件作用剪力分布 Figure 10 Shear force distribution of connectors |
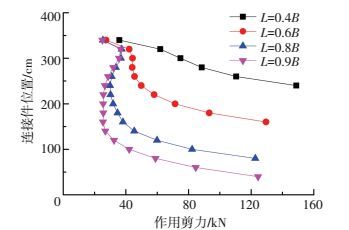
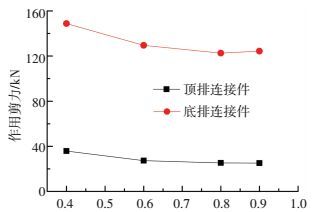
图 11给出了连接件竖向剪力值随结合部长度L变化的分布规律,B为单肢桥塔结合部纵桥向最大宽度.结合部长度L从0.4B增加到0.9B,连接件沿塔竖向间距不变. L取为0.4B时,连接件竖向剪力从顶部到底部近乎线性增加,数值由36 kN增加至150 kN. L增加后更多的连接件参与受力,底部连接件竖向剪力逐渐减小. 图 12给出了顶底排连接件随L/B变化的分布规律,当L/B超过0.8后,顶底排连接件竖向剪力变化较小.
|
图 11 结合部长度对连接件剪力的影响 Figure 11 Effects of composite joint length on shear force |
|
图 12 长宽比对连接件剪力的影响 Figure 12 Effects of length-width ratio on shear force |
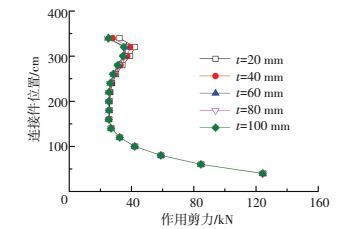
图 13给出了连接件竖向剪力值Vs随承压板厚度t变化的分布规律.承压板厚度变化对连接件竖向剪力Vs影响很小,仅结合部顶部承压板附近的几排连接件竖向剪力Vs有一定差异.
|
图 13 承压板厚度对连接件剪力的影响 Figure 13 Effects of bearing plate thickness on shear force |
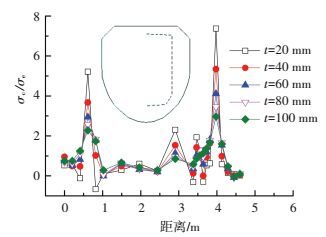
图 14给出了承压板厚度变化对承压板下部混凝土应力的影响. t由20 mm增加至100 mm,沿图中路径方向混凝土应力σc/平均应力σe的值由7.4降至3.钢塔过渡段的应力经过较厚的承压板扩散后,传力面积增大而压应力减小,混凝土的应力分布更为均匀.在结合部受力不利时,增加承压板厚度可以进一步改善混凝土受力.考虑承压板过厚会影响结合部的焊接性能,承压板厚度宜取60~80 mm.
|
图 14 承压板位置混凝土应力 Figure 14 Stress of concrete near bearing-plate |
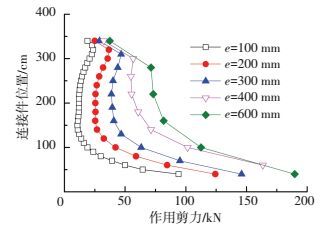
图 15给出了连接件竖向剪力值Vs随连接件间距e变化的分布规律.随着e的增加,各排连接件竖向剪力Vs逐渐增大,e由100 mm增加到600 mm时,底排连接件竖向剪力Vs由94 kN增加到190 kN,根据Vs分布可得出其间距取值不宜大于300 mm.
|
图 15 连接件间距对连接件剪力的影响 Figure 15 Effects of spacing on shear force |
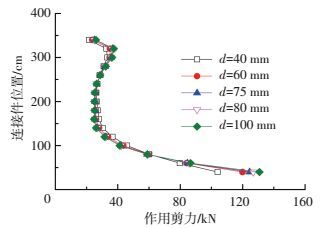
图 16给出了连接件竖向剪力值Vs随开孔板孔径d变化的分布规律.计算结果表明,d对连接件剪力Vs影响较小,仅对底排连接件Vs有一定影响. d由40 mm增加到100 mm时,底排连接件剪力Vs由104 kN增加到131 kN,而承载力则从131 kN增加到965 kN.考虑到大孔径对钢板的削弱作用,而传力比例变化并不显著,开孔板连接件孔径d宜取60~80 mm.
|
图 16 孔径对连接件剪力的影响 Figure 16 Effects of hole diameter on shear force |
1) 设计荷载作用下钢结构应力较为顺畅的传递到混凝土结构,相对滑移较小,后承压板式混合塔钢与混凝土结构结合性能较好.
2) 钢结构与混凝土结构之间的荷载主要靠承压板和连接件传递,分别分担了约40%和60%的荷载.荷载从1.0P提高到2.5P钢及混凝土结构应力均提高了约150%,结构处于弹性工作阶段,有较高的安全储备,钢-混凝土结合段设计较为保守,材料利用率低.
3) 距承压板0.6倍结合部长度范围内连接件竖向剪力及变化幅度均较小,在距承压板0.6~1.0倍结合部长度范围内连接件剪力逐渐增加,最底排连接件数值最大.结合部长度、连接件间距对连接件剪力影响较大,开孔板孔径、承压板厚度对连接件剪力影响较小.
4) 结合部长度宜取为塔肢纵桥向宽度,承压板厚度宜取为60~70 mm,连接件间距不宜大于300 mm,开孔板孔径宜取60~80 mm.
| [1] |
刘玉擎.
组合结构桥梁[M]. 北京: 人民交通出版社, 2005.
LIU Yuqing. Steel-concrete hybrid bridge[M]. Beijing: China Communications Press, 2005. |
| [2] |
卫星, 李小珍, 李俊, 等. 钢-混凝土混合结构在大跨度连续刚构桥中的应用[J].
中国铁道科学, 2007, 28(5): 43-46.
WEI Xing, LI Xiaozhen, LI Jun, et al. Using steel-concrete hybrid structure in long span continuous rigid frame bridge[J]. China Railway Science, 2007, 28(5): 43-46. |
| [3] |
张清华, 李乔, 唐亮. 桥塔钢-混凝土结合段剪力键破坏机理及极限承载力[J].
中国公路学报, 2007, 20(1): 85-90.
ZHANG Qinghua, LI Qiao, TANG Liang. Fracture mechanism and ultimate carrying capacity of shear connectors applied for steel-concrete joint segment of bridge pylon[J]. China Journal of Highway and Transport, 2007, 20(1): 85-90. |
| [4] |
司秀勇, 肖林, 赵建波. 斜拉桥桥塔钢-混凝土结合段模型试验研究[J].
中国铁道科学, 2011, 32(5): 26-31.
SI Xiuyong, XIAO Lin, ZHAO Jianbo. Model test research on the steel-concrete joint section of cable stayed bridge tower[J]. China Railway Science, 2011, 32(5): 26-31. |
| [5] | HE Jun, LIU Yuqing, PEI Bingzhi. Experimental study of the steel-concrete connection in hybrid cable-stayed bridges[J]. Journal of Performance of Constructed Facilities, 2014, 28(3): 559-570. DOI: 10.1061/(ASCE)CF.1943-5509.0000444 |
| [6] | LIU Rong, LIU Yuqing. Analysis of auxiliary ribs in steel-concrete joint of hybrid girder[J]. Journal of Constructional Steel Research, 2015, 112: 363-372. DOI: 10.1016/j.jcsr.2015.05.015 |
| [7] |
江祥林, 刘玉擎, 孙璇. 混合梁结合部受力机理模型试验研究[J].
土木建筑与环境工程, 2014, 36(6): 48-53.
JIANG Xianglin, LIU Yuqing, SUN Xuan. Modeltest and mechanical behavior analysis of steel-concrete joint of hybrid girder[J]. Journal of Civil, Architectural & Environmental Engineering, 2014, 36(6): 48-53. |
| [8] |
唐亮, 吴文明, 刘高, 等. 有格室-后承压板结合部构造的结构特性[J].
工程力学, 2010, 27(11): 234-243.
TANG Liang, WU Wenming, LIU Gao, et al. Structural performance of rear bearing-plate connection with cells in steel-concrete hybrid girder[J]. Engineering Mechanics, 2010, 27(11): 234-243. |
| [9] |
李小珍, 肖林, 黄玲, 等. 混合梁斜拉桥钢-混结合段静力行为[J].
哈尔滨工业大学学报, 2013, 45(6): 75-82.
LI Xiaozhen, XIAO Lin, HUANG Ling, et al. Static mechanical behavior of steel-concrete joint section of hybrid beam cable-stayed bridges[J]. Journal of Harbin Institute of Technology, 2013, 45(6): 75-82. DOI: 10.11918/j.issn.0367-6234.2013.06.014 |
| [10] |
卫星, 强士中. 斜拉桥桥塔钢-混凝土结合段传力机理试验研究[J].
工程力学, 2013, 30(1): 255-261.
WEI Xing, QIANG Shizhong. Specimen test for mechanics behavior of steel-concrete composite joint in pylon of cable-stayed bridge[J]. Engineering Mechanics, 2013, 30(1): 255-261. DOI: 10.6052/j.issn.1000-4750.2011.06.0351 |
| [11] |
肖林, 叶华文, 卫星, 等. 斜拉桥桥塔钢-混结合段的力学行为和传力机理研究[J].
土木工程学报, 2014, 47(3): 88-96.
XIAO Lin, YE Huawen, WEI Xing, et al. Study on mechanical behavior and load transfer mechanism of steel-concrete composite joint of cable-stayed bridge pylon[J]. China Civil Engineering Journal, 2014, 47(3): 88-96. |
| [12] |
赵晨, 刘玉擎. 开孔板连接件抗剪承载力试验研究[J]. 工程力学, 2012, 29(12): 349-354. DOI: 10.6052/j.issn.1000-4750.2011.09.0604.
ZHAO Chen, LIU Yuqing. Experimentalstudy of shear capacity of perfobond connector[J].2012, 29(12):349-354. DOI:10.6052/j.issn.1000-4750.2011.09.0604. |
| [13] |
赵晨. 开孔板连接件抗剪承载力及变形性能研究[D]. 上海: 同济大学, 2012.
ZHAO Chen. Research on shear capacity and deformation property of perfobond rib shear connector[D]. Shanghai: Tongji University, 2012. |
| [14] |
王倩, 刘玉擎. 焊钉连接件抗剪承载力试验研究[J].
同济大学学报 (自然科学版), 2013, 41(5): 659-663.
WANG Qian, LIU Yuqing. Experimental study of shear capacity of stud connector[J]. Journal of Tongji University (Natural Science), 2013, 41(5): 659-663. |
| [15] |
蔺钊飞, 刘玉擎. 焊钉连接件峰值滑移及剪力-滑移本构关系[J].
同济大学学报 (自然科学版), 2014, 42(7): 1006-1010.
LIN Zhaofei, LIU Yuqing. Peakslip and load-slip relationship of headed stud connectors[J]. Journal of Tongji University (Natural Science), 2014, 42(7): 1006-1010. |
 2017, Vol. 49
2017, Vol. 49


