2. 浙江大学宁波理工学院 土木建筑工程学院, 浙江 宁波 315100
2. School of Civil Engineering and Architecture, Ningbo Institute of Technology, Zhejiang University, Ningbo 315100, Zhejiang, China
近年来,结构健康监测 (structural health monitoring,SHM) 技术在桥梁结构中得到了广泛应用[1]. SHM系统获得的桥梁动静态及环境监测数据为结构损伤识别和状态评估提供了有效的数据支持,为研究桥梁结构的安全性及耐久性等问题提供了新的解决途径.
随着SHM在桥梁结构中的应用,基于SHM监测数据与可靠度理论的桥梁状态评估及预警方法尝试利用概率的思想解决影响桥梁性能因素随机性的问题[2].通过建立的桥梁结构的承载能力极限状态和正常使用极限状态的状态方程,从监测数据中提取出结构的真实荷载响应,利用可靠指标对桥梁系统或构件进行状态评估.文献[2]以有限元模型数值模拟的数据代替长期监测数据的方式对桥梁构件进行了可靠性评估.文献[3]利用实桥SHM系统长期监测数据对桥梁构件的可靠度进行了评估,实现了实桥状态评估的应用.随后,文献[4]利用SHM系统长期监测得到的车辆荷载响应,利用可靠度理论对桥梁的安全性能进行了评估.文献[5]利用东海大桥主航道斜拉桥15个月的长期监测数据,计算了桥梁构件的可靠指标和失效概率.文献[6]提出利用随机动载和静载共同作用下的可靠性模型对结构进行评估.文献[7]通过SHM系统监测的数据实现了青马大桥主缆的可靠性评估.文献[8]利用结构的动态检测信息,建立贝叶斯动态模型实现桥梁结构的可靠性评估.文献[9]以不同活载效应对应的可靠度建立了阈值区间,利用监测的活载应力,实现了连续刚构桥活载效应的预警.
综上所述,基于SHM监测数据与可靠度理论的桥梁状态评估方法,主要以车辆荷载效应为随机变量,并未考虑环境因素的影响.但是,对于混凝土连续箱梁桥,温度效应明显,甚至可能超过了活载效应.然而,考虑桥梁长期监测数据中温度效应的可靠性评估方法则未见报道.本文主要研究了车辆荷载和温度荷载共同作用下,基于混凝土连续箱梁桥SHM系统的监测数据的可靠性状态评估方法,为箱型截面混凝土桥梁的状态评估提供参考.
1 可靠度基本原理整个结构或结构的某一部分超过某种不能满足设计要求或功能要求的状态称为极限状态.极限状态是结构可靠与否的临界状态,可靠度则是判断结构是否到达临界状态的依据.根据桥梁结构的功能要求,建立功能函数或极限状态方程为
| $ Z\left( \mathit{\boldsymbol{X}} \right) = R\left( \mathit{\boldsymbol{X}} \right) - S\left( \mathit{\boldsymbol{X}} \right). $ | (1) |
其中:X=(X1, X2, …, Xn)T为影响桥梁结构功能的n个随机变量;X可以为桥梁结构的几何尺寸、材料力学性能参数及受到的作用等;R(X) 为结构的抗力;S(X) 为结构的各种作用效应.
功能函数Z可分为3种状态:Z>0,表示结构处于可靠状态;Z<0,表示结构处于失效状态;Z=0,表示结构处于极限状态或临界状态.结构的失效概率可表示为
| $ {p_{\rm{f}}} = P\left( {Z\left( \mathit{\boldsymbol{X}} \right) < 0} \right). $ | (2) |
在计算失效概率上,直接方法求解较困难,通常采用与失效概率有对应关系的可靠指标来表示.当结构抗力R和各种效应S的随机变量均服从正态分布且相互独立时,可靠指标β表示为
| $ \beta = \frac{{{\mu _{\rm{R}}} - {\mu _{\rm{S}}}}}{{\sqrt {\sigma _{\rm{R}}^2 + \sigma _{\rm{S}}^2} }}. $ | (3) |
其中:μR、μS分别为抗力和各种效应的平均值;σR、σS分别为抗力和各种效应的标准差.
失效概率pf与可靠指标β的关系可表示为
| $ {p_{\rm{f}}} = \mathit{\Phi }\left( { - \beta } \right) = 1 - \mathit{\Phi }\left( \beta \right). $ | (4) |
计算结构的可靠度方法主要有一次二阶距法及二次二阶距法等.一次二阶距法又分为中心点法和验算点法.中心点法的特点是可以不考虑变量的概率分布,基本的验算点法则只能处理正态分布.当基本变量中含有非正态随机变量时,可首先对随机变量当量正态化 (JC法)[10].本文采用了JC法进行可靠度计算.
3 极限状态方程的建立 3.1 实测响应成分分析对于既有混凝土箱梁桥,为了能够长期可靠的获得结构的静动态响应,避免外界恶劣环境对监测系统的影响,提高传感器的耐久性,通常采用在箱梁截面内表面表贴传感器的方式对结构进行监测.通过SHM系统实测的应变响应可表示为
| $ {\varepsilon _{\rm{M}}} = {\varepsilon _{\rm{T}}} + {\varepsilon _{{\rm{EF}}}} + {\varepsilon _{{\rm{IF}}}} + {\varepsilon _{\rm{C}}} + {\varepsilon _{\rm{N}}} + {\varepsilon _{\rm{O}}}. $ | (5) |
其中:εM为实测的应变;εT为温度作用产生的应变;εEF为外力作用产生的应变,对混凝土连续箱梁桥,主要指车辆荷载产生的应变;εIF为内力作用产生的应变,包括恒载和预应力产生的应变;εC为混凝土收缩徐变产生的应变;εN为测得的噪声;εO为偶然作用产生的应变.
从式 (5) 中可知,混凝土连续梁桥长期监测获得的应变响应是多种作用叠加的综合响应,但是,按照时间尺度划分,各种响应的作用周期则不尽相同.刘纲[11]对混凝土桥梁各种效应的时间尺度进行了分析:1) 桥梁结构的温度受地理条件、太阳辐射强度等外界环境因素影响,其表面温度变化的时间尺度与大气温度相同.在日温差、骤然降温和年温差对桥梁结构影响最大的3种温度模式中,日温差和年温差分别以天和年为时间尺度单位,骤然降温出现和持续的时间尺度具有随机性,可在几天之内完成;2) 车辆荷载在经过一座桥梁时,所持续时间较短,可以分钟为时间尺度;3) 混凝土收缩徐变效应的增长速度较缓慢,可认为在一个月之内收缩徐变的变化较小,以月为时间尺度对其进行衡量已具有足够精度;4) 桥梁结构的恒载和预应力的变化在结构运营中会经历较长期的变化过程,因此,以月为时间尺度单位也已具有足够的精度;5) 噪声的影响是一个随机过程,具有不确定性,可视为随机变量,其时间尺度分布在很宽的范围之内.因此,如以天为时间尺度单位对桥梁结构进行状态评估,只需考虑日温差、车辆荷载和噪声的影响.
3.2 正常使用极限状态方程对于受车辆荷载作用较小的桥梁,环境因素对桥梁结构的作用可能会大于车辆荷载的作用,为此,在进行桥梁结构的状态评估时,更应考虑桥梁结构的正常使用性能.规范[12]规定,当结构或结构构件出现下列状态之一时,应认为超过了正常使用极限状态:1) 影响正常使用或外观的变形;2) 影响正常使用或耐久性能的局部损坏;3) 影响正常使用的振动;4) 影响正常使用的其他特定状态.
混凝土连续箱梁桥在正常使用阶段,在时间尺度上如以天为参考周期,则主要受到日温差和车辆荷载的作用.其中,日温差最主要的效应是引起梁体纵向的伸缩变形和截面内竖向的温度梯度应力,整体温度变形对梁体的影响较小,因此,可主要考虑竖向的温度梯度荷载.在桥梁监测过程中,获得的各种响应均为“增量”响应,需计入结构的初始状态,即恒载内力.并且,可偏安全的以混凝土抗拉强度标准值作为抗力,以车辆荷载应力响应及温度梯度荷载应力响应作为荷载效应,从而建立混凝土连续箱梁桥截面内正常使用极限状态方程为
| $ \begin{array}{l} g = {s_{\rm{R}}}\left( {y,t} \right) + {\xi _0}\left( {y,t} \right){s_{\rm{H}}}\left( {y,t} \right) - \left( {1 + {e_1}} \right){\xi _1}\\ \;\;\;\;\;\;\left( {y,t} \right){s_{\rm{V}}}\left( {y,t} \right) - \left( {1 + {e_2}} \right){\xi _2}\left( {y,t} \right){s_{\rm{T}}}\left( {y,t} \right). \end{array} $ | (6) |
其中:sR(y, t) 为混凝土抗拉强度标准值;sR(y, t) 为成桥后的恒载效应;sV(y, t) 为实测的车辆荷载效应;sT(y, t) 为实测温度梯度荷载效应;ξ0(y, t) 为恒载效应的时间变异函数;ξ1(y, t) 为车辆荷载效应的时间变异函数;ξ2(y, t) 为温度梯度效应的时间变异函数,可通过ξ0(y, t)、ξ1(y, t) 和ξ2(y, t) 对未来的响应进行预测;e1和e2分别为监测误差,并且假设服从N(0, σ) 的正态分布.
可靠指标为
| $ {\beta _0} = \frac{{{\mu _{\rm{R}}} + {\mu _{\rm{H}}} - {\mu _{\rm{V}}} - {\mu _{\rm{T}}}}}{{\sqrt {\sigma _{\rm{R}}^2 + \sigma _{\rm{H}}^2 + \sigma _{\rm{V}}^2 + \sigma _{\rm{T}}^2} }}. $ | (7) |
其中:μR为混凝土抗拉强度标准值的均值;μH为恒载引起的应力的均值;μV为车辆荷载引起的应力的均值;μT为温度梯度荷载引起的应力的均值;σR为混凝土抗拉强度标准值的标准差;μH为恒载引起的应力的标准差;μV为车辆荷载引起的应力的标准差;σT为温度梯度荷载引起的应力的标准差.
在车辆荷载作用下,根据平截面假定,箱梁顶板沿桥梁纵向表现为受压,底板表现为受拉.因此,在计算顶板可靠指标时,根据最不利原则可不计算车辆荷载在顶板产生的效应.在温度梯度荷载作用下,顶底板均可能出现受拉情况.因此,可根据最不利效应组合对极限状态方程 (6) 进行变换,当计算顶板的可靠指标时,只计温度梯度荷载效应,极限状态方程可表示为
| $ {g_1} = {s_{\rm{R}}}\left( {y,t} \right) + {s_{\rm{H}}}\left( {y,t} \right) - \left( {1 + {e_2}} \right){\xi _2}\left( {y,t} \right){s_{\rm{T}}}\left( {y,t} \right). $ | (8) |
其可靠指标为
| $ {\beta _1} = \frac{{{\mu _{\rm{R}}} + {\mu _{\rm{H}}} - {\mu _{\rm{T}}}}}{{\sqrt {\sigma _{\rm{R}}^2 + \sigma _{\rm{H}}^2 + \sigma _{\rm{T}}^2} }}. $ | (9) |
当计算底板的可靠指标时,如温度梯度荷载效应表明底板为受压,只计车辆荷载效应,则极限状态方程可表示为
| $ {g_2} = {s_{\rm{R}}}\left( {y,t} \right) + {s_{\rm{H}}}\left( {y,t} \right) - \left( {1 + {e_1}} \right){\xi _1}\left( {y,t} \right){s_{\rm{V}}}\left( {y,t} \right). $ | (10) |
相应的,可靠指标为
| $ {\beta _2} = \frac{{{\mu _{\rm{R}}} + {\mu _{\rm{H}}} - {\mu _{\rm{V}}}}}{{\sqrt {\sigma _{\rm{R}}^2 + \sigma _{\rm{H}}^2 + \sigma _{\rm{V}}^2} }} $ | (11) |
综上所述,可归纳计算箱梁截面顶底板的可靠指标的流程如图 1所示.
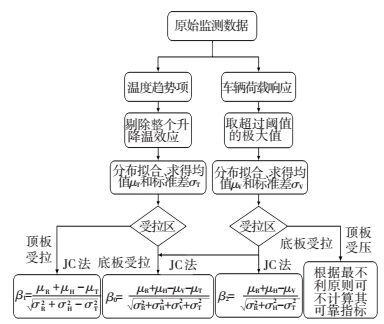
|
图 1 可靠指标计算流程图 Figure 1 Flow chart of reliability index calculation |
正常使用情况下,极限状态方程 (6) 需要满足以下假设条件:1) 在整体升降温作用下,箱梁截面内各点的纵向应变变化相同.混凝土箱梁各点处材料特性的差异及受力的不均匀性,均可能导致截面内温度效应的不同,假设截面内材料对温度的敏感性差异 (或线膨胀系数的差异) 是很小的,忽略其影响. 2) 假设在整个监测过程中箱梁满足平截面假定. 3) 假设以天计的趋势项应变,只由整体升降温产生的应变与温度梯度产生的应变组成.由上文的分析可知,如以天为监测周期,恒载、收缩徐变等效应均可忽略,只考虑温度效应. 4) 不考虑箱梁截面的畸变效应.
4 算例分析 4.1 富绥大桥长期监测系统简介富绥松花江公路大桥位于黑龙江省绥滨县境内,于富锦市和绥滨县间跨越松花江,路线全长14.448 km.主桥为预应力混凝土连续箱梁,跨径布置为85 m+ 6×150 m+ 85 m,全长1 070 m.主桥分为上下游两幅,单幅桥宽11.25 m,中间0.5 m分隔带,全宽23 m.采用双向四车道设计,荷载等级为公路-I级,设计时速为60 km/h,于2011年10月份建成通车.富绥大桥长期监测系统共52个传感器,分别对结构跨中挠度、应变、加速度和温度进行长期监测,传感器纵向布置如图 2所示.现场B断面的传感器布置如图 3(a)所示,D断面的应变布置如图 3(b)所示.富绥大桥健康监测系统的详细介绍见参考文献[13].
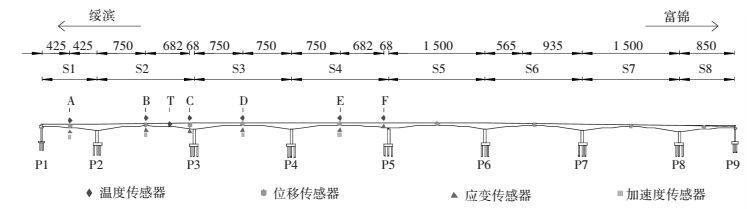
|
图 2 传感器纵向布置图 (cm) Figure 2 Layout of sensors in longitudinal direction (cm) |

|
图 3 传感器断面布置图 Figure 3 Layout of sensors in cross-section |
选取富绥大桥2012年6月14日至2012年6月23日D断面的顶底板实测应变响应进行分析. 图 4为D断面应变传感器DS1的实测应变响应.在实测应变响应中,以天为周期的波动较明显,这是由于日照产生的整体温度效应,通常可认为是信号中的长期趋势项.

|
图 4 DS1应变响应原始信号 Figure 4 Original time history curves of strain responses of DS1 |
从原始信号中分离趋势项的方法主要有经验模态分解 (EMD) 法、低通滤波法和最小二乘法等.本文采用EMD方法对趋势项进行了分离.常规的EMD方法是将信号直接分解,得到各阶的瞬时频率 (IMF),把残差作为最终的趋势项[14].但对于长期监测的动态信号,数据量较大,如直接用EMD算法对信号求解IMFs,迭代计算每阶IMF的过程将占用大量的CPU内存及花费大量的时间.
本文采用了一种先分段、再合并的信号提取趋势项的方法,该方法可大大缩短计算的时间,有效降低长期监测数据的趋势项提取造成的计算成本和时间成本.信号趋势项的提取步骤如下:1) 设实测信号为y(t),信号长度为n,分成i段,每段信号长度为k=n/i,则实测信号y(t) 被分成k段,记为y1(t1)、y2(t2)、…、yi(ti);2) 对每段数据进行“降采样”处理. “降采样”频率fj与原采样频率fy的关系为fj=fy/m,其中m为采样间隔. “降采样”后的数据表示为y1′(t1)、y2′(t2)、…、yi′(ti).其目的是可进一步降低EMD方法中迭代计算的数据量;3) 对数据yi′(ti) 采用EMD方法得到残差趋势项ci(ti);4) 通过三次样条插值法,对残差趋势项ci(ti) 进行“升采样”,得到与原数据yi(ti) 相同长度的趋势项
应用上述趋势项分离方法,可获得D断面DS1测点剔除趋势项后的信号如图 5,趋势项信号如图 6.从图 5中可以看出,信号存在比较明显的尖峰,即为车辆经过桥梁时产生的应变响应.箱梁顶板主要产生负向的应变尖峰 (表示受压),箱梁底板主要产生正向的应变尖峰 (表示受拉).因此,从各传感器应变尖峰的大小和数量上可以对车辆荷载效应进行判断.
|
图 5 DS1剔除趋势项后的应变信号 Figure 5 Processed time history curves of strain responses of DS1 |
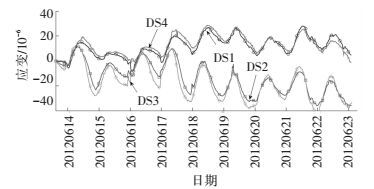
|
图 6 应变响应的趋势项 Figure 6 Trend terms of the strain responses |
对提取的趋势项信号以天为周期进行分段,设置每天的零点时刻为“相对零起点”,其目的是清除前一天的累积效应的影响,使每天的趋势项中只包含当天的温度效应.根据截面内各点在整体温度作用下纵向变形相同,通过顶底板的应变趋势项相减,即可消除整体升降温的影响,得到顶底板温度梯度作用下的应变响应.
整个监测过程中,混凝土的应力-应变关系满足胡克定律,即σ=E·ε,其中σ为应力,ε为实测应变,E为混凝土弹性模量.取施工阶段实测的28 d混凝土的弹性模量均值4.1×104 MPa.从而,可将实测的应变转换成应力进行分析.
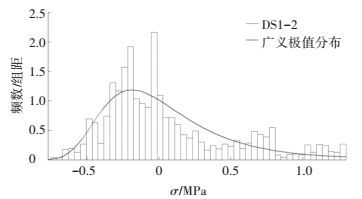
利用MATLAB数据分析软件对箱梁顶底板的温度梯度应力进行了概率密度函数拟合. 图 7为温度梯度荷载产生的顶底板相对应力的直方图及广义极值分布 (GEV) 的概率密度函数的拟合曲线.由于每天的温度梯度荷载随机性比较大,因此,概率密度函数的拟合结果存在一定的误差,但可近似认为温度梯度荷载产生的应力满足GEV分布.
4.4 车辆荷载应力概率密度函数拟合目前,对车辆荷载产生的应力的取值分为两种方式.一种是直接应用,文献[3]利用直接监测的车辆荷载数据对结构进行可靠度评估.另一种方式是取车辆荷载应力的极值[15].车辆荷载应力极值选取的两种方法是:1) 采用每天的最大值作为监测极值;2) 设定一个阈值,取超过阈值的监测极值[4].本文采取后者,选取超过阈值的监测极值研究车辆荷载应力的概率密度分布函数.通过对实测数据的分析发现,绝对值小于0.06 MPa的极值均为噪声引起,因此,取绝对值大于0.06 MPa的极大值进行分析.
|
图 7 温度梯度荷载应力直方图和GEV概率密度函数 Figure 7 Histogram of temperature gradient stress and GEV probability density function |
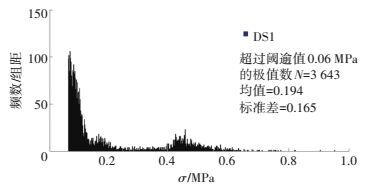
图 8为DS1监测的应力极值的直方图.统计得到超过0.06 MPa的极值数共计3 643个,车辆荷载的应力均值0.194 MPa,其标准差为0.165.车辆荷载应力响应的直方图出现了两处峰值,即在相对较低的应力区间内存在明显的峰值,稍远区间内还存在着另外一处峰值.因此,对实测的应力极值进行了进一步“筛选”:DS1和DS3取阈值0.25 MPa,DS2和DS4取阈值0.3 MPa.
|
图 8 DS1车辆荷载应力直方图 Figure 8 Histogram of vehicle induced stress of DS1 |
利用MATLAB数据分析软件,分别对D断面DS1~DS4超过阈值的应力直方图应用广义极值、对数正态、韦伯和正态概率密度函数进行了拟合, 如图 9所示.概率密度函数拟合的极大似然值结果如表 1所示,可以看出,DS1和DS3的应力极值采用GEV分布和对数分布拟合结果相差非常小,DS2和DS4的应力极值采用广义极值分布拟合结果明显优于其他分布类型,因此,可认为车辆荷载效应服从广义极值分布.

|
图 9 DS1车辆荷载应力直方图及概率密度函数 Figure 9 DS1 histogram of vehicle induced stress and probability density functions |
| 表 1 车辆荷载应力概率密度函数拟合的极大似然值 Table 1 Maximum likelihood value results of probability density function of vehicle induced stresses |
根据上文的可靠度评估方法,按照图 1的计算流程,对箱梁顶底板在车辆荷载和温度梯度荷载作用下的应变响应的拉压情况进行最不利组合:在车辆荷载作用下,位于箱梁底板的DS1和DS4传感器监测的应变响应大于零,表明底板受拉,应变响应小于零,表明底板受压;在温度梯度荷载作用下,顶底板的受拉情况根据同侧顶板 (DS2和DS3) 和底板 (DS1和DS4) 传感器监测的应变响应的差值决定,底板和顶板应变差值大于零,表明底板受拉,底板和顶板应变差值小于零,表明顶板受拉.可靠指标的计算组合见表 2.
| 表 2 可靠指标计算组合 Table 2 Calculation combination of reliability index |
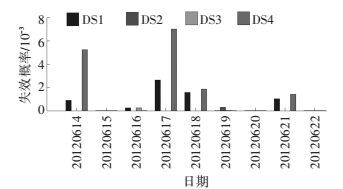
根据公路桥梁设计规范,取C50混凝土的抗拉强度标准值2.65 MPa为抗力均值,变异系数取0.15[16].车辆荷载应力及温度梯度应力的均值和标准差均按照每天监测数据进行计算.最终,可计算出每天各测点的可靠指标和失效概率如图 10、11所示.

|
图 10 可靠指标计算结果 Figure 10 Calculated results of reliability indexes |
|
图 11 失效概率计算结果 Figure 11 Calculated results of failure probabilities |
通过图 10计算的可靠指标可知,6月14日、6月17日、6月18日、6月21日4 d的DS1和DS4底板位置的可靠指标均接近3,顶板位置DS2和DS3可靠指标未计算,表明车辆荷载和温度梯度荷载均在底板产生了拉应力,造成底板的可靠指标非常小,相应的失效概率显著增加. 图 11中箱梁顶底板失效概率均小于1%,表明在车辆荷载和温度梯度荷载的共同作用下,底板出现裂缝的可能性会相应增大,然而,整体的失效概率还很小,结构处于安全状态.同时,如果温度梯度荷载在顶板产生拉应力,车辆荷载在底板产生拉应力,则测点处的可靠指标均较大,相应的失效概率非常小,表明在正常使用状态下处于安全状态.
5 结论1) 基于可靠度理论提出的混凝土箱梁桥状态评估方法,考虑了车辆荷载和竖向温度梯度的共同作用,为评估混凝土箱梁桥的安全状态提出了一种新的思路.
2) 对于数据量较大的信号,可对数据进行分段处理,并对分段信号进行“降采样”,进一步缩短信号长度,通过经验模态分解方法提取趋势项,再按照三次样条插值法将每段残差信号恢复到原有长度,进而合并成原始信号的趋势项.该方法可有效提高提取趋势项的计算效率.
3) 温度梯度荷载应力和车辆荷载应力采用广义极值分布的概率密度函数拟合效果较好.
4) 在车辆荷载和竖向温度梯度单项荷载作用下,顶底板均处于安全状态;当两者共同作用下,底板的可靠指标显著降低,底板开裂的可能性升高.
| [1] |
李惠, 周文松, 欧进萍, 等. 大型桥梁结构智能健康监测系统集成技术研究[J].
土木工程学报, 2006, 39(2): 46-52.
LI Hui, ZHOU Wensong, OU Jinping, et al. A study on system integration technique of intelligent monitoring systems for soundness of long span bridges[J]. China Civil Engineering Journal, 2006, 39(2): 46-52. |
| [2] | NI Y Q, HUA X G, KO J M. Reliability-based assessment of bridges using long-term monitoring data[J]. Advanced Nondestructive Evaluation I, 2006, 321-323: 217-222. |
| [3] | FRANGOPOL D M, STRAUSS A, KIM S Y. Bridge reliability assessment based on monitoring[J]. Journal of Bridge Engineering, 2008, 13(3): 258-270. DOI: 10.1061/(ASCE)1084-0702(2008)13:3(258) |
| [4] | LIU M, FRANGOPOL D M, KIM S Y. Bridge safety evaluation based on monitored live load effects[J]. Journal of Bridge Engineering, 2009, 14(4): 257-269. DOI: 10.1061/(ASCE)1084-0702(2009)14:4(257) |
| [5] |
焦美菊, 孙利民, 李清富. 基于监测数据的桥梁结构可靠性评估[J].
同济大学学报 (自然科学版), 2011, 39(10): 1452-1457.
JIAO Meiju, SUN Limin, LI Qingfu. Bridge structural reliability assessment based on health monitoring data[J]. Journal of Tongji University (Natural Science), 2011, 39(10): 1452-1457. DOI: 10.3969/j.issn.0253-374x.2011.10.007 |
| [6] |
李锋, 孟广伟, 周立明, 等. 复杂载荷作用下结构的可靠性研究[J].
哈尔滨工业大学学报, 2011, 43(Sup1): 295-298.
LI Feng, MENG Guangwei, ZHOU Liming, et al. Reliability for structures under complex load[J]. Journal of Harbin Institute of Technology, 2011, 43(Sup1): 295-298. |
| [7] | LI S L, ZHU S Y, XU Y L, et al. Long-term condition assessment of suspenders under traffic loads based on structural monitoring system: Application to the Tsing Ma Bridge[J]. Structural Control and Health Monitoring, 2012, 19(1): 82-101. DOI: 10.1002/stc.427 |
| [8] |
樊学平, 吕大刚. 基于DLM的桥梁结构承载力的贝叶斯预测[J].
哈尔滨工业大学学报, 2012, 44(12): 13-17.
Fan Xueping, LÜ Dagang. Bayesian prediction of structural bearing capacity of aging bridges based on dynamic linear model[J]. Journal of Harbin Institute of Technology, 2012, 44(12): 13-17. DOI: 10.11918/j.issn.0367-6234.2012.12.003 |
| [9] |
吴海军, 李俊, 黄友帮, 等. 大跨径连续刚构桥在活载单项作用下的预警级别[J].
重庆交通大学学报 (自然科学版), 2014, 33(5): 29-31.
WU Haijun, LI Jun, HUANG Youbang, et al. Warning level of large-span continuous rigid frame bridge in single live load[J]. Journal of Chongqing Jiaotong University (Natural Science), 2014, 33(5): 29-31. |
| [10] | RACKWITZ R, FLESSLER B. Structural reliability under combined random load sequences[J]. Computers & Structures, 1978, 9(5): 489-494. DOI: 10.1016/0045-7949(78) |
| [11] |
刘纲. 基于长期静态监测数据的大型桥梁安全状态评估方法研究[D]. 重庆: 重庆大学, 2010.
LIU Gang. Condition assessment research to large-span bridges based on long-term static monitoring data[D]. Chongqing :Chongqing University, 2010. |
| [12] |
公路工程结构可靠度设计统一标准: GB/T 50283—1999[S]. 北京: 中国计划出版社, 1999.
Unified standard for reliability design of highway engineering structures: GB/T 50283—1999[S]. Beijing: China Planning Press, 1999. |
| [13] | CHEN C, KALOOP M R, GAO Q F, et al. Environmental effects and output-only model identification of continuous bridge response[J]. KSCE Journal of Civil Engineering, 2015, 19(7): 2198-2207. DOI: 10.1007/s12205-014-0280-1 |
| [14] |
陈隽, 徐幼麟. 经验模分解在信号趋势项提取中的应用[J].
振动、测试与诊断, 2005, 25(2): 101-104.
CHEN Jun, XU Youlin. Application of EMD to signal trend extraction[J]. Journal of Vibration, Measurement & Diagnosis, 2005, 25(2): 101-104. DOI: 10.4028/www.scientific.net/AMR.591-593.2072 |
| [15] | STRAUSS A, FRANGOPOL D M, KIM S Y. Use of monitoring extreme data for the performance prediction of structures: Bayesian updating[J]. Engineering Structures, 2008, 30(12): 3654-3666. DOI: 10.1016/j.engstruct.2008.06.009 |
| [16] |
禹智涛. 既有钢筋混凝土桥梁可靠性评估的若干问题研究[D]. 广州: 华南理工大学, 2003.
YU Zhitao. Several problems of existing reinforced concrete bridge reliability evaluation[D]. Guangzhou: South China University of Technology, 2003. |
 2017, Vol. 49
2017, Vol. 49


