2. 哈尔滨工业大学 土木工程学院,哈尔滨 150090
2. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China
随着公路运输日趋渠化和重型化,重载货运汽车行驶振动促使路基振动问题日益突出,长期交通荷载下路基产生不可恢复的塑性变形,不断加剧沥青路面的车辙与水泥路面的开裂等病害.特别是在雨水丰富且最大冻结深度大于路面结构层厚度的季节性冻土地区,路基表层范围内的冻胀敏感性土体在冬季时水分冻结、聚冰,春融期融化,如此反复的冻结与融化作用使得路基土体物理和力学性能发生剧烈的改变[1-3];加之重载交通荷载的反复作用,由此诱发路基产生大量的塑性变形,严重影响路面的使用寿命和功能.因此,明确季冻区长期重载交通荷载下的路基永久变形发展,对提高寒区公路路基的设计水平有重要的理论意义和实际意义.
“力学-经验法”是获取长期循环交通荷载作用下路基永久变形的常用方法[4],该方法基于路基土的永久应变经验模型、路基的应力分布状态以及分层总和原理.近年来,国内外一些学者考虑了土体含水率、压实度、围压、动应力、应力水平、频率和应力历史等条件的影响,获得土体在循环荷载下的塑性累积永久应变经验模型[5-6];同时,在交通荷载作用下路基的动力响应的解析解[7-8]和数值解[9-13]方面也取得较多的成果.为了预测长期交通荷载下路基的永久变形,文献[14]提出了循环荷载下砂土的累积塑性应变模型,并计算了路基永久变形.文献[15]采用动偏应力与总应变的关系刻画土体的应变硬化现象,并预测了循环荷载作用下颗粒材料的永久变形.文献[16]采用力学经验法计算了长期循环荷载作用下柔性路面的永久变形.文献[17]基于路基土的残余应变特性与孔隙水压力变化规律,提出了交通荷载作用下湿软路基残余变形的计算方法.文献[18]考虑了轮迹横向分布频率,提出了柔性路面路基土在车辆重复荷载作用下永久变形的改进计算方法.文献[19]发现路基顶面竖向累积永久变形曲线在道路横断面上的分布形态呈“勺子”形.可见,目前所采用的公路交通荷载形式过于简化,且未考虑冻融作用对路基永久变形的影响.
因此,本文首先基于路基融土永久应变经验模型,提出季节冻土区长期公路交通荷载作用下路基永久变形计算方法;其次,通过基层-路基-地基动力有限元模型,计算分析了汽车轴型、后轴轴重、行车速度和冻融影响路基厚度对路基最大应力比和永久变形的影响;最后,提出了季节冻土区长期交通荷载作用下路基永久应变预测公式.
1 路基永久变形计算方法基于长期交通荷载下路基融土永久应变模型[20],采用分层总和法计算路基永久变形,步骤如下.
步骤1 确定路基土体静强度qf.在静力有限元分析中,假设路基土体为非线性弹性模型,通过计算获取路基的自重应力σcz分布,进而采用下式计算静强度qf[21].
| ${q_{\rm{f}}} = 2{\tau _{\rm{f}}} = \frac{{2{c_{{\rm{cu}}}}{\rm{cos}}{\varphi _{{\rm{cu}}}}}}{{1 - {\rm{sin}}{\varphi _{{\rm{cu}}}}}} + {\sigma _{{\rm{cu}}}}\frac{{\left( {1 + {K_0}} \right){\rm{sin}}{\varphi _{{\rm{cu}}}}}}{{1 - {\rm{sin}}{\varphi _{{\rm{cu}}}}}}.$ | (1) |
式中:τf为抗剪强度;K0为侧限系数;ccu为粘聚力;φcu为内摩擦角;σcu为自重应力.
步骤2 确定路基土体动偏应力qd.在动力有限元分析中,假定土体为粘弹性模型,通过计算获取路基的动应力分布,用下式计算土体的动偏应力.
| ${q_{\rm{d}}} = \sqrt {3{J_2}} .$ | (2) |
式中J2为第二动偏应力不变量.
步骤3 路基土体最大应力比Smax.在动力有限元分析中,按下式计算路基的应力比,并确定每一个单元的最大应力比Smax.
| $S = {q_{\rm{d}}}/{q_{\rm{f}}}.$ | (3) |
式中qd为动偏应力,qf为静强度.
步骤4 单元土体永久应变εp.给定的荷载作用次数N和单元最大应力比Smax时,根据下式路基融土永久应变模型[20],确定单元引起的永久应变εp.
| ${\varepsilon _{\rm{p}}} = \frac{N}{{1000}}{\left[ {a + b{{\left( {\frac{N}{{1000}}} \right)}^m}} \right]^{ - \frac{1}{m}}}.$ | (4) |
式中:εp为永久应变;N为荷载作用次数;a、b和m均为模型参数,为应力比S的函数,受路基土体含水量、围压、冻融循环次数的影响.
步骤5 确定土体永久变形Dp.基于分层总和方法,按下式分层累加,获取路基永久变形Dp.
| ${D_{\rm{p}}} = \sum\limits_{i = 1}^k {{\varepsilon _{{\rm{pi}}}}{h_i}} .$ | (5) |
式中hi为第i个单元厚度,εpi为第i个单元的永久应变.
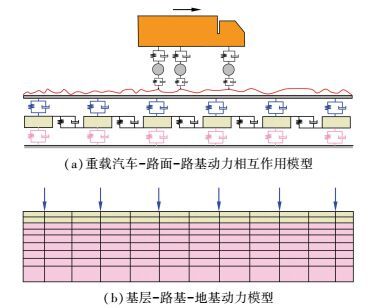
2 重载车荷载下路基的动力响应 2.1 建模思路首先,将重载汽车简化为多自由度匀速移动的质量、弹簧和阻尼体系,如图 1(a)所示,路面视为连续粘弹性薄板模型,基层视为离散的剪切质量块模型,推导并建立重载汽车-路面-路基动力相互作用模型[22],计算获取面层与基层之间的作用力时程.进而以此为输入,建立基层-路基-地基动力有限元模型,得到公路交通荷载作用下路基的动力响应.
|
图 1 重载汽车荷载作用下路基动力响应的求解 Figure 1 Models for solving dynamic response of subgrade under heavy truck loading |
假设基层、路基和地基为各向同性材料,建立路基动力有限元分析模型,动力方程为
| $\left[ M \right]\left\{ {\ddot x} \right\} + \left[ C \right]\left\{ {\dot x} \right\} + \left[ K \right]\left\{ x \right\} = \left\{ P \right\}.$ | (6) |
式中:[M]、[K]和[C]分别为质量矩阵、刚度矩阵和阻尼矩阵,{P}为荷载向量,{x}、
采用Reyleigh阻尼形式,其表达式为
| $\left[ C \right] = \alpha \left[ M \right] + \beta \left[ K \right].$ | (7) |
式中α、β均为常数,满足α=λω,β=λω-1,其中λ为土的阻尼比,ω为自振圆频率.
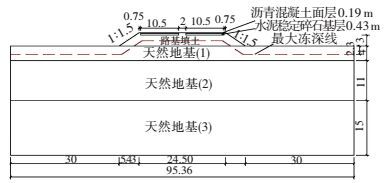
2.3 计算模型以齐—嫩高速公路某段路基为例,计算模型见图 2.采用四边形等参数单元,静力有限元计算中,底部为竖向约束,左右两侧边界为水平向约束;动力有限元计算中,底部和两侧边界为人工粘性边界.
|
图 2 齐—嫩高速公路某段路基几何模型 (m) Figure 2 Geometric model of a subgrade section in Qiqihar-Nenjiang highway (m) |
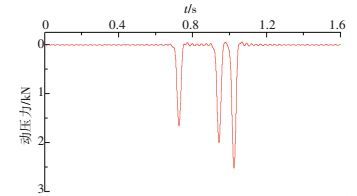
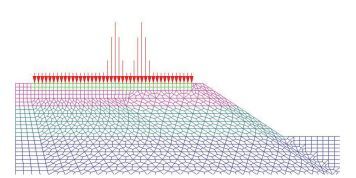
使用重载汽车-路面-路基动力分析程序DATPS[20]得到了后轴轴重100 kN、行车速度为60 km/h时的基层顶面的应力时程,轮迹带下基层顶面节点动荷载时程见图 3,将其作为路基动力有限元分析模型的输入,基层顶面动荷载加载方式见图 4.
|
图 3 轮迹带下路基顶面某节点动荷载时程曲线 Figure 3 Dynamic force-time curve under the truck tire |
|
图 4 基层顶面动荷载的输入方式 Figure 4 Input model of dynamic loading on top of base |
表 1为基层、路基土和地基土的物理力学参数.其中,春融期路基温度是随时间连续变化的,本文将未融化的冻结路基温度分别假定为一个恒定温度-2 ℃,以简化考虑冻土物理力学参数的变化,同时假定正常期路基,以及春融期路基冻结层和融化层水平呈层状分布,且厚度相同.
| 表 1 基层和路基土物理力学参数 Table 1 Parameters of base materials and subgrade soil |
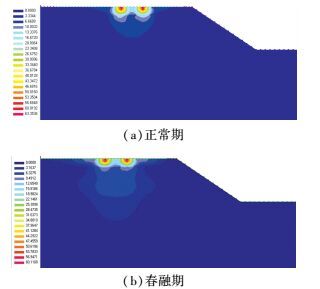
图 5、6分别为正常期和春融期路基最大动偏应力和最大应力比分布.可见,交通荷载下基层和路基的动偏应力呈纺锤状分布,随埋深的增加逐渐减小;由于正常期和春融期路基土的模型参数不同,动偏应力分布不同.春融期时路基表层处于融化状态,故动偏应力明显小于正常期;当路基土冻结时,动偏应力明显大于正常期,其原因在于土体模量的大小:土体模量较大,动偏应力较大;土体模量减弱,动偏应力减小.
|
图 5 正常期和春融期时的最大动偏应力分布 (kPa) Figure 5 Distribution of maximum deviator stress in normal season and spring thaw season (kPa) |
|
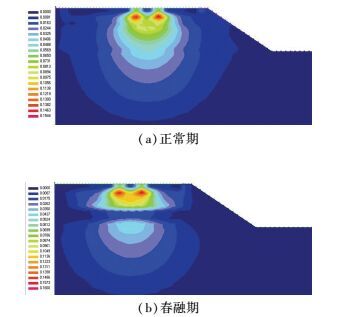
图 6 正常期和春融期时的最大应力比分布 Figure 6 Distribution of maximum stress ratio in normal season and spring thaw season |
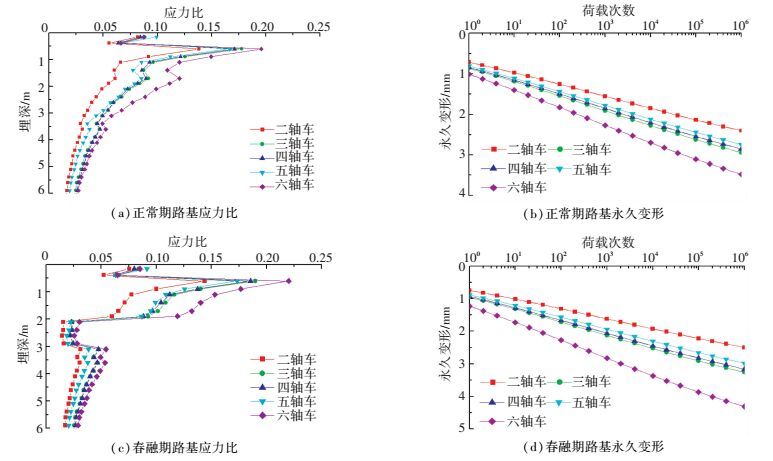
当后轴轴重为100 kN、行车速度60 km/h时,不同汽车轴型时路基最大应力比和永久变形曲线见图 7.可见,相同路基结构层内,应力比随埋深的增加逐渐衰减,由于各结构层的静力性能不同,在结构层分界面处出现突变现象。相同埋深时,二轴车产生的最大应力比最小,三轴、四轴和五轴车相差不大,六轴车产生的最大应力比最大;春融期时路基融化层内产生的最大应力比较大,冻结层内的最大应力比小很多.荷载循环次数对路基永久变形的影响显著,随着循环荷载次数的增加,路基的永久变形逐渐增大;双轴车产生的路基永久变形小,三轴、四轴和五轴车相差不大,六轴车产生的变形大.
|
图 7 汽车轴型对路基应力比和永久变形的影响 Figure 7 Effect of axle types on stress ratio and permanent deformation of subgrade |
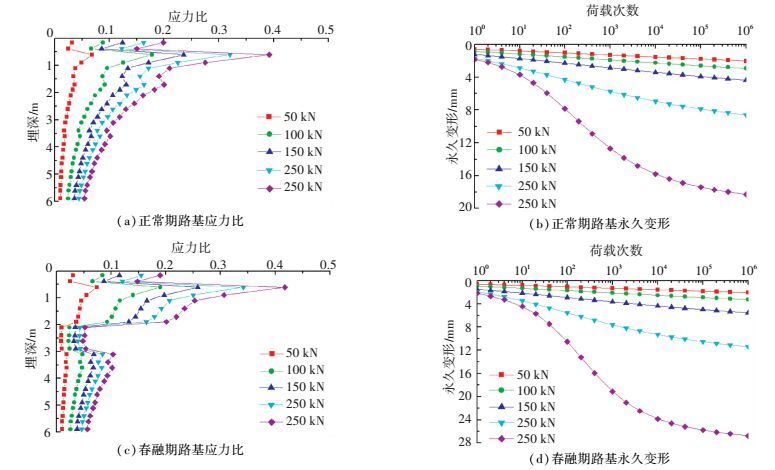
当行车速度为60 km/h时,不同后轴轴重产生路基最大应力比和永久变形曲线见图 8.后轴轴重对路基内最大应力比和永久变形的发展影响显著;随着后轴轴重从50 kN逐渐增加至250 kN,同一埋深的最大应力比成倍增加.春融期时,由于路基表层土体静强度较正常期低,所以融化层内最大应力比明显大于正常期时的,相应地,长期荷载作用下路基土体的永久变形也大于正常期.此外,后轴轴重小于200 kN时,荷载次数与永久变形呈对数关系增长形式;后轴轴重为200 kN和250 kN时,路基永久变形随荷载作用次数迅速增加.
|
图 8 后轴轴重对路基应力比和永久变形的影响 Figure 8 Effect of rear axle on stress ratio and permanent deformation of subgrade |
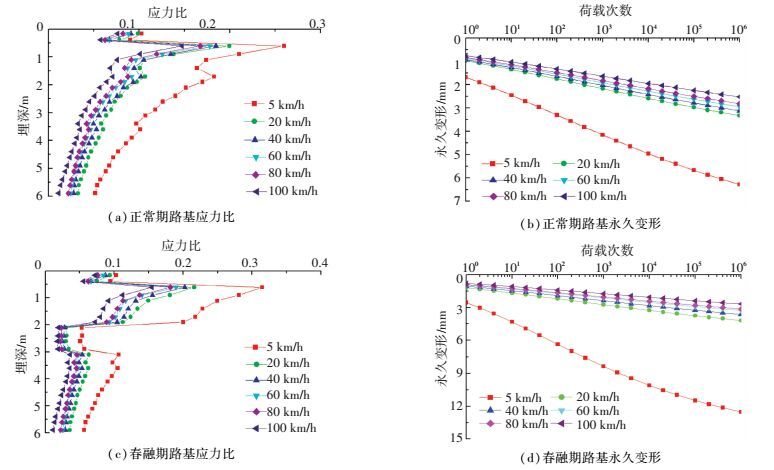
当后轴轴重为100 kN时,不同行车速度下产生路基最大应力比和永久变形曲线见图 9.整体而言,行车速度对路基最大应力比和永久变形的发展皆有较明显的影响.行车速度较小时,路基内产生较大的应力比和永久变形;行车速度增大时,同一埋深下路基内最大应力比逐渐减小.主要是因为,当行车速度较高时,荷载的作用率大,同一位置路基应力作用时间较短,且路基动力响应中占主导地位的高频成分易被土体吸收;而当行车速度较低时,荷载的作用率小,同一位置路基应力作用时间较长,路基动应力以低频传播为主,易被土体吸收的振动成分相对较少,因此动压应力能够传递至更深位置;长期公路交通荷载作用下,较低速度要比较高行车速度产生的永久变形要大.特别当行车速度为5 km/h时,相同深度的路基应力比较大,相同荷载次数作用下,路基的永久变形显著.
|
图 9 行车速度对路基应力比和永久变形的影响 Figure 9 Effect of driving speed on stress ratio and permanent deformation of subgrade |
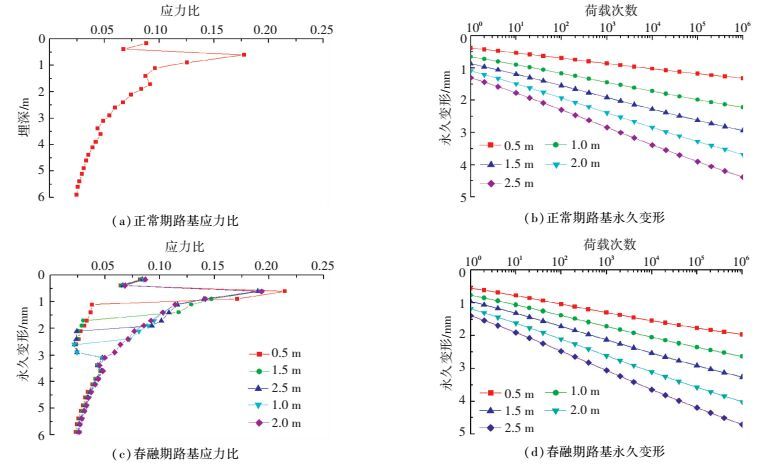
当后轴轴重为100 kN,行车速度为60 km/h时,不同的路基内路基最大应力比和永久变形曲线见图 10.可见,正常期内不同的路基厚度范围内,土体的永久变形不同.随厚度的增加,相同荷载作用次数下土体的永久变形增加;然而,由于路基深部应力比浅层小,因此,当冻融影响路基厚度逐渐增加时,相同荷载作用次数下土体的永久变形的增加幅度降低.春融期时,路基的融化厚度增加,路基应力比较大的区域明显增加.主要是因为,路基表层冻融后,融化层土体的物理、力学结构改变,路基土体的模量和静强度降低,所以应力比相对增加.而且,值得关注的是,相同厚度与荷载作用次数时,春融期路基产生的永久变形比正常期时大.
|
图 10 冻融路基厚度对路基应力比和永久变形的影响 Figure 10 Effect of freeze-thaw influence depth on stress ratio and permanent deformation of subgrade |
以三轴重载汽车、后轴轴重100 kN和行驶速度为60 km/h、路基计算厚度1.5 m对应的路基永久变形为基准条件,建立综合考虑各因素对路基永久应变的影响的路基永久变形的预测公式为
| ${\varepsilon _{\rm{p}}} = {c_{{\rm{al}}}}{c_{{\rm{vt}}}}{c_{{\rm{rs}}}}{c_{{\rm{de}}}}\frac{N}{{1\;000}}{\left[ {{a_0} + {b_0}{{\left( {\frac{N}{{1\;000}}} \right)}^{{m_0}}}} \right]^{ - \frac{1}{{{m_0}}}}}.$ | (8) |
式中:εp为路基顶面永久应变; N为荷载次数; cal、cvt、crs、cde分别为汽车轴型、后轴轴重、行车速度和冻融影响路基厚度修正系数,取值分别见表 2~5;a0、b0、m0为基准应力比时对应的模型参数.
| 表 2 不同汽车轴型时的修正系数 Table 2 Correction factors for different axle type of truck |
| 表 3 不同后轴轴重时修正系数 Table 3 Correction factors for different rear axle of truck |
| 表 4 不同行车速度时的修正系数 Table 4 Correction factors for different driving speed |
| 表 5 不同冻融路基厚度时的修正系数 Table 5 Correction factors for different freeze-thaw influence depth |
1) 基于室内试验获取的路基融土永久应变经验公式,提出了季节冻土区长期公路交通荷载作用下路基永久变形计算步骤,计算并分析了不同的汽车轴型、后轴轴重、行车速度和路基冻融厚度对路基应力比和永久变形的影响.
2) 正常期时路基内部的最大应力比随埋深增加逐渐减小;春融期时,融化层内最大应力较正常期大,冻结层内较正常期小.汽车轴型、后轴轴重、行车速度和冻融路基厚度对正常期和春融期内路基的最大应力比分布影响显著.
3) 六轴重载汽车产生的永久应变较其他4种轴型汽车的大.随着后轴轴重和路基冻融厚度的增加,路基内最大应力比和永久变形显著增加.行车速度越低,路基内最大应力比和永久变形越小.
4) 采用基准条件可以获的其他行车因素和路基冻结与融化状态下的永久变形.今后的研究还应从路基的温度、湿度,以及路面结构层等因素完善该预测模型.
| [1] | SIMONSENE, JANOO V C, ISACSSON U. Resilient properties of unbound road materials during seasonal frost conditions[J]. Journal of Cold Regions Engineering, 2002, 16(1): 28-50. DOI: 10.1061/(asce)0887-381x(2002)16:1(28) |
| [2] | QI Jilin, MA Wei, SONG Chunxia. Influence of freeze-thaw on engineering properties of a silty soil[J]. Cold Regions Science and Techno-logy, 2008, 53(3): 397-404. DOI: 10.1016/j.coldregions.2007.05.010 |
| [3] |
李玉浓, 张喜发, 冷毅飞, 等. 季冻区高速公路路基冻害调查及实验观测[J].
哈尔滨工业大学学报, 2010, 42(4): 617-623.
LI Yunong, ZHANG Xifa, LENG Yifei, et al. Investigation on freeway subgrade frost damage in seasonally frozen ground[J]. Journal of Harbin Institute of Technology, 2010, 42(4): 617-623. DOI: 10.11918/j.issn.0367-6234.2010.04.024 |
| [4] | AASHTO. Guide formechanistic-empirical design of new and rehabilitated pavement structures[R]. Washington DC: National Cooperative Highway Research Program, 2004. |
| [5] | MONISMITH C L, OGAWA N, FREEME C R. Permanent deformation characteristics of subgrade soils due to repeated loading[J]. Transportation Research Record, 1975, 537: 1-17. DOI: 10.1061/jhtrcq.0000059 |
| [6] | LI D, SELIG E T. Cumulative plastic deformation for fine-grained subgrade soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1996, 122(12): 1006-1013. DOI: 10.1061/(asce)0733-9410(1996)122:12(1006) |
| [7] | ADERSEN L, NIELSEN S R K. Boundary element analysis of the steady-state response of an elastic half-space to a moving force on its surface[J]. Engineering Analysis with Boundary Elements, 2003, 27(1): 23-38. DOI: 10.1016/s0955-7997(02)00096-6 |
| [8] | FRANCOIS S, LOMGAERT G, DEGRANDE G. Local and global shape functions in a boundary element formulation for the calculation of traffic induced vibrations[J]. Soil Dynamics and Earthquake Enginnering, 2005, 25(11): 839-856. DOI: 10.1016/j.soildyn.2005.05.002 |
| [9] | LAK M A, DEGRANDE G, LOMBAERTG. The effect of road unevenness on the dynamic vehicle response and ground-borne vibrations due to road traffic[J]. Soil Dynamics and Earthquake Engineering, 2011, 31(10): 1357-1377. DOI: 10.1016/j.soildyn.2011.04.009 |
| [10] |
刘飞禹, 蔡袁强, 余炜, 等. 移动荷载下无面层加筋路基的动力响应[J].
哈尔滨工业大学学报, 2009, 41(2): 145-149.
LIU Feiyu, CAI Yuanqiang, YU Wei, et al. Dynamic response of reinforced unpaved subgrade subjected to moving loads[J]. Journal of Harbin Institute of Technology, 2009, 41(2): 145-149. |
| [11] |
丁凯, 金波. 移动荷载作用下地基动力分析的有限元方法[J].
力学季刊, 2006, 27(4): 648-654.
DING Kai, JIN Bo. The finite element method for dynamic analysis of foundation under moving loads[J]. Chinese Quarterly of Mechanics, 2006, 27(4): 648-654. DOI: 10.3969/j.issn.0254-0053.2006.04.017 |
| [12] |
杨佳松, 金波. 移动荷载下多孔饱和地基的动力有限单元法[J].
力学季刊, 2009, 30(1): 101-108.
YANG Jiasong, JIN Bo. Dynamic finite element method for poroelastic foundation subjected to moving loads[J]. Chinese Quarterly of Mechanics, 2009, 30(1): 101-108. |
| [13] | ZHAI Wei, SONG Erxiang. Three dimensional fem of moving coordinates for the analysis of transient vibrations due to moving loads[J]. Computers and Geotechnics, 2010, 37(1): 164-174. DOI: 10.1016/j.compgeo.2009.08.007 |
| [14] | WICHTMANN T, NIEMUNIS A, TRIANTAFYLLIDIS T. Strain accumulation in sand due to drained cyclic loading: on the effect of monotonic and cyclic preloading (miner's rule)[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(8): 736-745. DOI: 10.1016/j.soildyn.2010.03.004 |
| [15] | KHOGALI W E I, MOHAMED E H H. Novel approach for characterization of unbound material[C]//83rd Annual TRB Meeting of the Transportation Meeting Board. Washington DC:National Research Council, 2004: 210-223. DOI: 10.3141/1874-05. |
| [16] | UZAN J. Permanent deformation in flexible pavements[J]. Journal of Transportation Engineering, 2004, 130(1): 6-13. DOI: 10.1061/(asce)0733-947x(2004)130:1(6) |
| [17] |
凌建明, 王伟, 邬洪波. 行车荷载作用下湿软路基残余变形的研究[J].
同济大学学报, 2002, 30(11): 1315-1320.
LING Jianming, WANG Wei, WU Hongbo. On residual deformation of saturated clay subgrade under vehicle load[J]. Journal of Tongji University, 2002, 30(11): 1315-1320. DOI: 10.3321/j.issn:0253-374X.2002.11.007 |
| [18] |
李冬雪, 凌建明, 钱劲松, 等. 黏质路基土永久变形改进计算方法[J].
同济大学学报 (自然科学版), 2013, 41(3): 386-389.
LI Dongxue, LING Jianming, QIAN Jinsong, et al. Improved calculation method of permanent deformation for cohesion subgrade soil[J]. Journal of Tongji University (Natural Science), 2013, 41(3): 386-389. |
| [19] |
黄琴龙, 杨传景, 韩秉烨, 等. 运煤公路黄土路基不均匀永久变形特性[J].
重庆交通大学学报 (自然科学版), 2015, 34(6): 63-67.
HUANG Qinlong, YANG Chuanjing, HAN Bingye, et al. Non-uniform permanent deformation characteristics of coal highway loess subgrade[J]. Journal of Chongqing Jiaotong University (Natural Science), 2015, 34(6): 63-67. |
| [20] |
张锋. 深季节冻土区重载汽车荷载下路基动力响应与永久变形[D]. 哈尔滨: 哈尔滨工业大学, 2012.
ZHANG Feng. Dynamic response and permanent deformation of subgrade induced by heavy truck load in deep seasonally frozen region[D]. Harbin:Harbin Institute of technology, 2012. |
| [21] |
沈珠江. 基于有效固结应力理论的粘土土压力公式[J].
岩土工程学报, 2000, 22(3): 353-356.
SHEN Zhujiang. Earth pressure of clay based on effective consolidation stress theory[J]. Chinese Journal of Geotechnical Engineering, 2000, 22(3): 353-356. DOI: 10.3321/j.issn:1000-4548.2000.03.019 |
| [22] |
张锋, 冯德成, 凌贤长, 等. 重载汽车-路面-路基垂向耦合动力学模型[J].
中国公路学报, 2015, 28(4): 1-12.
ZHANG Feng, FENG Decheng, LING Xianzhang, et al. Vertical coupling dynamic model of heavy truck-pavement-subgrade[J]. China Journal of Highway and Transport, 2015, 28(4): 1-12. |
 2017, Vol. 49
2017, Vol. 49


