2. 青岛理工大学 汽车与交通学院,山东 青岛 266520
2. School of Automobile and Transportation, Qingdao Technology University, Qingdao 266520, Shandong, China
准确、可靠的交通流预测信息可以直接应用于先进的交通管理系统 (advanced traffic management system,ATMS) 和先进的交通信息服务系统 (advanced traffic information service system,ATIS),为出行者提供实时有效的交通运行信息,从而缩短出行时间,缓解交通拥堵.目前,已有许多成熟的理论和方法应用于短时交通流预测的研究,如时间序列模型[1-3],非参数回归模型[4],卡尔曼滤波模型[5-6],神经网络模型[7-8],支持向量机模型[9-10]等.随着对交通流特性的深入研究以及混沌理论的发展,越来越多的学者提出基于混沌理论的短时交通流预测方法.此类方法可以不必事先建立主观模型,而直接根据交通流时间序列数据本身计算得到的非线性特征和规律进行预测[11],避免了主观建模时受到的人工干预,能够有效提高预测的精度和可靠度.现有的混沌预测方法主要分为全局预测和局域预测两类,其中,全局预测是根据相空间中所有相点刻画其演化规律,然后根据规律预测未来值;局域预测仅对N个邻近相点进行拟合,刻画出相点的短暂演化规律,进而得到预测值.如文献[12]通过分析交通流时间序列数据的混沌特性确定嵌入维数和延迟时间,并以重构的相空间数据作为输入数据,采用Elman神经网络模型实现道路网多断面交通流全局预测.文献[13]基于混沌理论对交通流时间序列进行相空间重构,并针对局域自适应预测方法中预测器系数无法调节的问题,提出了交通流多步自适应局域预测方法.局域预测方法具有拟合相点数量少、计算复杂度低、拟合度高等优点.文献[14]已经证明在相同的嵌入维数下,局域预测的效果明显优于全局预测.因此,本文采用局域预测方法对短时交通流进行预测.由于现有交通流局域预测方法大多采用线性方式拟合邻域内相点的演变规律,而交通系统是一种典型的非线性动力系统,其演化规律也应该是非线性的.针对上述问题,本文提出基于组合核相关向量机模型的短时交通流局域预测方法.在相空间重构的基础上,应用Hannan-Quinn准则确定邻近点个数,进而构建基于粒子群优化的组合核函数相关向量机模型,并采用上海市南北高架快速路的感应线圈实测数据进行实例验证,对模型的有效性进行测试.
1 相空间重构相空间重构 (phase space reconstruction, PSR) 是一种根据有限的数据来重构吸引子以研究系统动力学行为的方法[15],已成为研究复杂交通系统的有力工具.根据Takens提出的嵌入延迟定理,选择合适的延迟时间τ和嵌入维数m可以获得与原系统具有相同动态特性的新系统.设长度为N的交通流时间序列数据{x(i), i=1, 2, …, N},则重构后的相空间为
| $X\left( i \right)=\left\{ x\left( i \right),x\left( i+\tau \right),\cdots ,x\left[ i+\left( m-1 \right)\tau \right] \right\}.$ | (1) |
合适的嵌入维数和延迟时间是实现相空间重构的关键,目前已有多种确定嵌入维数和延迟时间的方法,其中,由文献[16]提出的C-C法可以同时估计出延迟时间和嵌入窗宽,具有操作简单、计算量小、抗干扰性强等优点.因此,本文选取C-C法来确定延迟时间τ和嵌入维数m.下面说明C-C方法的基本原理.
C-C方法是利用时间序列的关联积分函数估计时间延迟τ和延迟时间窗τw=(m-1)τ,进而获得嵌入维数m,关联积分定义为
| $\begin{align} &C\left( m,N,r,\tau \right)=\frac{2}{M\left( M-1 \right)}\sum\limits_{1\le i < j\le M}{\theta \left( r- \right.} \\ &\left. \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{\left\| X\left( i \right)-X\left( j \right) \right\|}_{\infty }} \right). \\ \end{align}$ | (2) |
其中:N为时间序列长度,r为邻域半径,M=N-(m-1)τ为相空间中相点数量,θ(·) 为Heaviside单位函数,若x < 0,θ(x)=0;若x≥0,θ(x)=1.
将时间序列{x(i), i=1, 2, …, N}分成t个互不相关的子序列,定义其检验统计量为
| $\begin{align} &S\left( m,N,r,t \right)=\frac{1}{t}\sum\limits_{l=1}^{t}{\left[ {{C}_{l}}\left( m,\frac{N}{r},r,t \right)- \right.} \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left. C_{l}^{m}\left( 1,\frac{N}{r},r,t \right) \right]. \\ \end{align}$ | (3) |
当N→∞时,
| $S\left( m,r,t \right)=\frac{1}{t}\sum\limits_{l=1}^{t}{\left[ {{C}_{l}}\left( m,r,t \right)-C_{l}^{m}\left( 1,r,t \right) \right].}$ | (4) |
根据BDS统计结论,取m=2, 3, 4, 5,
| $\bar{S}\left( t \right)=\frac{1}{16}\sum\limits_{m=2}^{5}{\sum\limits_{j=1}^{4}{S\left( m,{{r}_{j}},t \right),}}$ | (5) |
| $\Delta \bar{S}\left( t \right)=\frac{1}{4}\sum\limits_{m=2}^{5}{\max \left\{ S\left( m,{{r}_{i}},t \right) \right\}}-\min \left\{ S\left( m,{{r}_{j}},t \right) \right\},$ | (6) |
| ${{S}_{\text{cor}}}\left( t \right)=\Delta \bar{S}\left( t \right)+\left| \bar{S}\left( t \right) \right|.$ | (7) |
其中最佳延迟时间τ对应于ΔS(t) 取第一个极小值时的时间,延迟时间窗τw对应于Scor(t) 取全局最小值时对应的时间.
2 组合核相关向量机模型构建相关向量机 (relevance vector machine,RVM) 模型是由Tipping提出的一种稀疏贝叶斯概率模型,已成为近年来统计学习领域的重要研究热点之一.该算法起源于支持向量机 (support vector machine,SVM) 模型,与SVM具有相同的决策形式,同时拥有SVM所不具备的优点,例如RVM具有优于SVM的稀疏性,只需设置核参数,对核函数的选择突破了Mercer条件限制等.关于相关向量机模型的原理详见参考文献[17].本文针对相关向量机模型的核函数选择问题,将具有不同特点的核函数结合起来,构建一种组合核函数相关向量机 (combined kernel function relevance vector machine,CKF-RVM) 模型.
2.1 组合核函数构造传统的相关向量机模型大多采用单一核函数完成特征空间的映射过程,虽然在许多实际应用中取得了较好的效果,但当样本数据特征中含有异构信息、样本规模较大或样本数据在高维空间中分布不平坦时[18],采用单一核函数映射方式对所有样本数据进行处理具有较大的局限性.因此,本文综合高斯核函数和多项式核函数各自的优势,构造新的组合核函数,使相关向量机模型不仅具有高斯核函数的局部学习能力,并且具有多项式核函数较强的泛化能力.构造的组合核函数形式为
| $\begin{matrix} K\left( x,{{x}_{i}} \right)=\lambda \cdot \exp \left( -\frac{{{\left\| x-{{x}_{i}} \right\|}^{2}}}{2{{\sigma }^{2}}} \right)+ \\ \left( 1-\lambda \right)\cdot {{\left( x{{x}_{i}}+1 \right)}^{d}}. \\ \end{matrix}$ | (8) |
其中:λ为权重系数,0≤λ≤1;σ为高斯核函数的核宽度;d为多项式核函数的阶数.
2.2 基于粒子群算法的参数优化组合核函数中共有λ、σ、d3个待优化参数,目前较为常用的参数优化方法主要有交叉验证法、网格搜索法、遗传算法等,但这些方法往往计算量较大、耗时过长.粒子群算法是一种高效的全局优化方法,已被广泛应用于参数的优化设置.因此,本文采用粒子群优化 (particle swarm optimization,PSO) 算法获取组合核函数的最优参数,粒子群优化算法利用相空间重构之后的历史数据确定3个待优化参数,进而构建组合核相关向量机模型.
粒子群优化算法的具体步骤如下:1) 初始化粒子群优化算法的参数.包括种群规模、粒子维数、迭代次数、加速因子、惯性权重系数等.2) 采用预测结果的平均绝对百分比误差作为适应度函数值,并将其与自身的历史最佳位置适应度值进行比较,如果当前位置的适应度值优于历史适应度值,则将当前位置取代个体历史最佳位置.3) 判断粒子群的全局最佳位置.将各个粒子的个体最佳位置适应度值与群体的全局最佳位置适应度相比较,若优于群体的全局适应度,则将其位置取代全局最佳位置.4) 判断终止条件.若不满足终止条件,则更新粒子的速度和位置,否则输出得到的最优解.
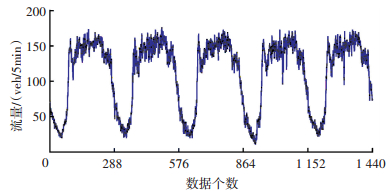
3 实例验证 3.1 数据来源实验数据来源于上海市南北高架快速路上延东立交至共和立交长约10 km路段感应线圈检测器采集到的交通流数据,该路段包括24个主线检测截面和30个匝道检测截面,共布设88个主线线圈检测器和60个匝道线圈检测器,主线检测器的平均间距约为500 m.数据采集时间分别为2008年9月1日、8日、15日、22日和29日连续5个星期一,线圈检测器可获取流量、速度和占有率3个基本交通参数,数据采样间隔为5 min,每个星期一采集288个数据.图 1为连续5个星期一的交通流数据.
|
图 1 连续5个星期一的交通流数据 Figure 1 Traffic flow data from five consecutive Mondays |
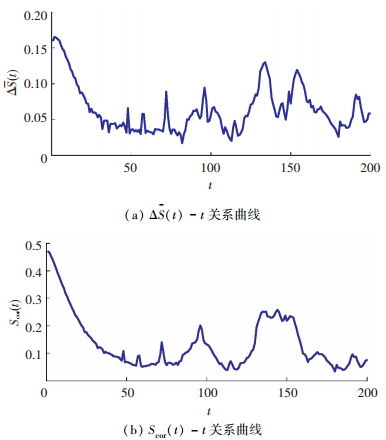
相空间重构是进行混沌时间序列分析的前提,采用C-C方法获得ΔS(t)-t和Scor(t)-t的关系曲线如图 2所示.
|
图 2 C-C方法计算结果 Figure 2 Calculated results of C-C method |
由图 2(a)可见,当ΔS(t) 取第一个极小值时t=18,即时间延迟τ取18.由图 2(b)可见,Scor(t) 取全局最小值时t=113,即延迟时间窗τw=113,进而根据τw=(m-1)τ可得嵌入维数m=7.
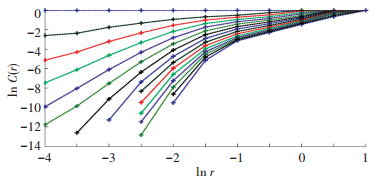
3.3 混沌特性识别通过计算关联维数对交通流数据进行混沌特性识别,其中嵌入维数m取值为1~15,则交通流数据的ln C(r)-ln (r) 关系如3所示,C(r) 为相关函数,r为临界距离.
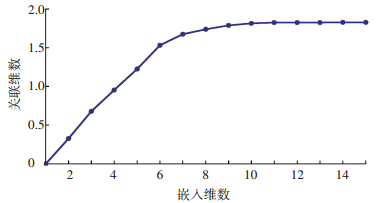
从图 3中选取线性关系较好的一段ln (r)∈[-2.5, -1.5]作为无标度区间,然后计算其斜率作为关联维数值,则可得关联维数与嵌入维数的关系如图 4所示.由图 4可见,关联维数随着嵌入维数的增加逐渐达到饱和,关联维数的饱和值为1.826,说明交通流时间序列数据存在混沌特性.
|
图 3 交通流数据ln C(r)-ln (r) 曲线 Figure 3 The lnC(r)-ln (r) curve of traffic flow data |
|
图 4 关联维数与嵌入维数关系 Figure 4 The relationship between correlation dimension and embedding dimension |
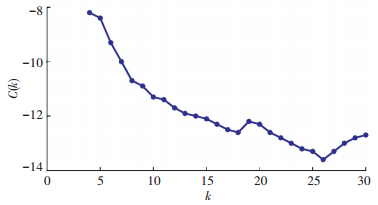
邻近点个数是局域预测的关键参数,本文应用Hannan-Quinn准则[19]来确定局域预测的邻近点个数.由图 5可见,当k=26时,C(k) 取得最小值,因此,局域预测方法的邻近点个数取为26.
|
图 5 基于Hannan-Quinn准则的邻近点个数 Figure 5 The number of neighboring points based on Hannan-Quinn criteria |
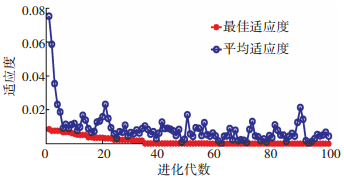
采用粒子群优化算法对组合核函数的λ、σ、d3个参数进行寻优,粒子群优化算法的具体参数设置如下:粒子个数为20,加速因子c1=c2=2,惯性权重系数从0.9随迭代次数线性减小至0.4,最大迭代次数为100.将9月1日、8日、15日、22日4 d的相空间重构数据作为训练样本,采用平均绝对百分比误差 (mean absolute percentage error,MAPE) 作为适应度函数值.适用度曲线如图 6所示.
|
图 6 PSO寻优适应度曲线 Figure 6 The fitness curve of PSO |
由粒子群优化结果可知,组合核函数最优参数分别为λ=0.67,σ=0.25,d=3.
3.6 实验结果分析为了评估组合核相关向量机模型在短时交通流预测上的实际应用效果,将9月29日的数据作为测试样本对模型的预测性能进行评估.采用平均绝对百分比误差 (mean absolute percentage error,MAPE) 和均等系数 (equal coefficient,EC) 两个指标进行评价.
| $\text{MAPE=}\frac{1}{n}\sum\limits_{i=1}^{n}{\left| \frac{{{y}_{i}}-{{{\hat{y}}}_{i}}}{{{y}_{i}}} \right|},$ | (9) |
| $\text{EC=1-}\frac{\sqrt{\sum\limits_{i=1}^{n}{\left( {{y}_{i}}-{{{\hat{y}}}_{i}} \right)}}}{\sqrt{\sum\limits_{i=1}^{n}{y_{i}^{2}}}+\sqrt{\sum\limits_{i=1}^{n}{\hat{y}_{i}^{2}}}}.$ | (10) |
其中:yi为i时刻的实际值;
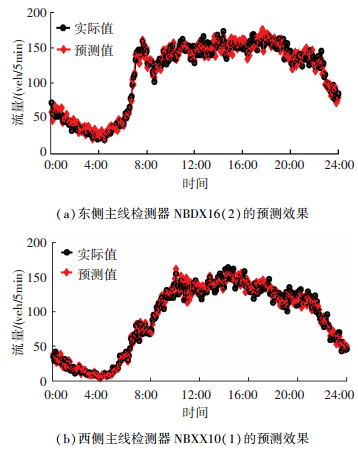
为直观展现本文方法的预测效果,图 7给出了预测值与实际值的拟合效果.其中,图 7(a)、7(b)分别为东侧主线检测器NBDX16(2) 和西侧主线检测器NBXX10(1) 的预测效果.
|
图 7 本文方法的预测效果 Figure 7 Prediction performance based on the proposed method |
由图 7的预测结果可见,本文方法得到的预测值与实际值之间拟合效果较好,能够满足短时交通流预测的需求.
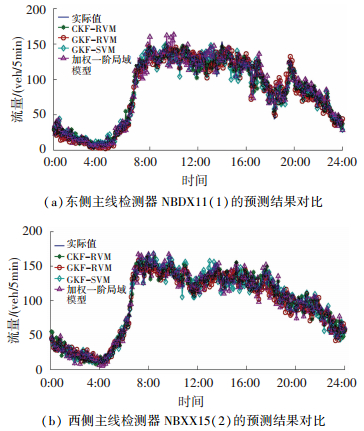
为了详细描述本文方法在短时交通流预测上的优越性,选取高斯核函数相关向量机 (Gaussian kernel function relevance vector machine,GKF-RVM) 模型、高斯核函数支持向量机 (Gaussian kernel function support vector machine,GKF-SVM) 模型和加权一阶局域预测模型作为对比方法,从微观和宏观两个角度进行对比分析.图 8(a)和图 8(b)分别为不同方法对东侧主线检测器NBDX11(1) 和西侧主线检测器NBXX15(2) 的预测结果.表 1为不同方法的宏观对比结果.
|
图 8 不同方法的微观对比结果 Figure 8 Microscopic comparative results of different methods |
| 表 1 不同方法的预测效果 Table 1 Prediction performance of different methods |
从图 8的预测结果可以清楚的看到,相比于GKF-RVM模型、GKF-SVM模型和加权一阶局域预测模型,CKF-RVM模型的预测结果与实际值拟合效果最好,说明本文方法的预测效果明显优于另外3种对比方法.
由表 1的预测结果可见:1) CKF-RVM模型、GKF-RVM模型和GKF-SVM模型的短时交通流局域预测效果均优于加权一阶局域预测模型的预测效果,说明利用非线性拟合方式能够更加精确的表征交通流数据的特性,可以有效提高短时交通流预测的精度.2) CKF-RVM模型和GKF-RVM模型的预测效果均优于GKF-SVM模型和加权一阶局域预测模型,说明相关向量机模型在短时交通流预测上的有效性.3) 对比CKF-RVM模型和GKF-RVM模型的预测效果可见,CKF-RVM模型的预测效果更优,说明采用组合核函数构建相关向量机模型的有效性.4) 本文方法在东侧主线和西侧主线均获得了较好的预测效果,说明CKF-RVM模型具有较强的泛化能力.
4 结论1) 提出了一种混沌理论的短时交通流局域预测方法.该方法以相空间重构为基础,根据Hannan-Quinn准则确定邻近点个数,综合高斯核函数和多项式核函数的优势构造新的组合核函数,进而构建基于粒子群优化的组合核相关向量机模型.
2) 以上海市南北高架快速路的感应线圈实测数据为例进行实验验证和对比分析.实验结果表明,本文提出的CKF-RVM模型的预测结果与实际值拟合效果较好,且在MAPE和EC两方面均优于GKF-RVM模型、GKF-SVM模型和加权一阶局域预测模型,同时具有较强的泛化能力.
3) 基于混沌理论的短时交通流局域预测方法只考虑了单一交通参数的预测,没有考虑交通参数之间存在的内在相关性,下一步的研究重点将集中在多变量相空间重构及其局域预测.
| [1] | ISHAK S, AL-DEEK H. Performance evaluation of short-term-series traffic prediction model[J]. Journal of Transportation Engineering, 2002, 128(6): 490-498. DOI: 10.1061/(ASCE)0733-947X(2002)128:6(490) |
| [2] | MIN W, WYNER L. Real-time road traffic prediction with spatio-temporal correlation[J]. Transportation Research Part C: Emerging Technologies, 2011, 19(4): 606-616. DOI: 10.1016/j.trc.2010.10.002 |
| [3] |
邴其春, 杨兆升, 周熙阳, 等. 基于向量误差修正模型的短时交通参数预测[J].
吉林大学学报 (工学版), 2015, 45(4): 1076-1081.
BING Qichun, YANG Zhaosheng, ZHOU Xiyang, et al. Short-term traffic parameters prediction method based on vector error correction model[J]. Journal of Jilin University (Engineering and Technology Edition), 2015, 45(4): 1076-1081. DOI: 10.13229/j.cnki.jdxbgxb201504008 |
| [4] | CLARK S. Traffic prediction using multivariate nonparametric regression[J]. Journal of Transportation Engineering, 2003, 129(2): 161-168. DOI: 10.1061/(ASCE)0733-947x(2003)129:2(161) |
| [5] |
杨兆升, 朱中. 基于卡尔曼滤波理论的交通流量实时预测模型[J].
中国公路学报, 1999, 12(3): 63-67.
YANG Zhaosheng, ZHU Zhong. A real-time traffic volume prediction model based on the kalman filtering theory[J]. China Journal of Highway and Transport, 1999, 12(3): 63-67. |
| [6] | WANG Y, PAPAGEORGOION M. Real-time freeway traffic state estimation based on extended kalman filter: a general approach[J]. Transportation Research Part B: Methodological, 2005, 39(2): 141-167. DOI: 10.1016/j.trb.2004.03.003 |
| [7] |
龚勃文, 林赐云, 李静, 等. 基于核自组织映射-前馈神经网络的交通流短时预测[J].
吉林大学学报 (工学版), 2011, 41(4): 938-943.
GONG Bowen, LIN Ciyun, LI Jing, et al. Short-term traffic flow prediction based on KSOM-BP neural network[J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(4): 938-943. |
| [8] | ZHU J Z, CAO J X, ZHU Y. Traffic volume forecasting based on radial basis function neural network with the consideration of traffic flows at the adjacent intersections[J]. Transportation Research Part C:Emerging Technology, 2014, 47(2): 139-154. |
| [9] |
杨兆升, 王媛, 管青. 基于支持向量机方法的短时交通流量预测方法[J].
吉林大学学报 (工学版), 2006, 36(6): 881-884.
YANG Zhaosheng, WANG Yuan, GUAN Qing. Short-term traffic flow prediction method based on SVM[J]. Journal of Jilin University (Engineering and Technology Edition), 2006, 36(6): 881-884. |
| [10] |
傅贵, 韩国强, 逯峰, 等. 基于支持向量机回归的短时交通流预测模型[J].
华南理工大学学报 (自然科学版), 2013, 41(9): 71-76.
FU Gui, HAN Guoqiang, LU Feng, et al. Short-term traffic flow forecasting model based on support vector machine regression[J]. Journal of South China University of Technology (Natural Science Edition), 2013, 41(9): 71-76. DOI: 10.3969/j.issn.1000-565X.2013.09.012 |
| [11] |
王进, 史其信. 基于非线性理论的短期交通流预测研究[J].
西安建筑科技大学学报 (自然科学版), 2006, 38(2): 184-188.
WANG Jin, SHI Qixin. Study of the short-term traffic flow forecasting based on nonlinear theory[J]. Journal of Xian University of Architecture and Technology (Natural Science Edition), 2006, 38(2): 184-188. |
| [12] |
董春娇, 邵春福, 李娟, 等. 基于混沌分析的道路网交通流短时预测[J].
系统工程学报, 2011, 26(3): 340-345.
DONG Chunjiao, SHAO Chunfu, LI Juan, et al. Short-term traffic flow prediction of road network based on chaos theory[J]. Journal of System Engineering, 2011, 26(3): 340-345. |
| [13] |
张洪宾, 孙小端, 贺玉龙. 短时交通流复杂动力学特性分析及预测[J].
物理学报, 2014, 63(4): 1-8.
ZHANG Hongbin, SUN Xiaoduan, HE Yulong. Analysis and prediction of complex dynamical characteristics of short-term traffic flow[J]. Acta Physica Sinica, 2014, 63(4): 1-8. DOI: 10.7498/aps.63.040505 |
| [14] | FARMER J D, SIDOROWICH J J. Prediction chaotic time series[J]. Physical Review Letters, 1987, 59(8): 845-848. DOI: 10.1103/PhysRevLett.59.845 |
| [15] | PACKARD N H, CRUTCHFIELD J P, FARMER J D. Geometry from a time series[J]. Physical Review Letters, 1980, 45(9): 712-716. DOI: 10.1103/PhysRevLett.45.712 |
| [16] | KIM H S, EYKHOLT R, SALAS J D. Nonlinear dynamics, delay times, and embedding windows[J]. Physical D, 1999, 127: 48-60. DOI: 10.1016/S0167-2789(98)00240-1 |
| [17] | TIPPING M E. Sparse Bayesian learning and the relevance vector machine[J]. Journal of Machine Learning Research, 2001, 1(3): 211-244. |
| [18] |
瞿娜娜. 基于组合核函数支持向量机研究及应用[D]. 广州: 华南理工大学, 2011.
QU Nana.Research and application of support vector machine based on mixed-kenel function[D].Guangzhou: South China University of Technology, 2011. |
| [19] |
孟庆芳, 彭玉华, 曲怀敬, 等. 基于信息准则的局域预测法邻近点的选取方法[J].
物理学报, 2008, 57(3): 1423-1430.
MENG Qingfang, PENG Yuhua, QU Huaijing, et al. The neighbor point selection method for local prediction based on information criterion[J]. Acta Physica Sinica, 2008, 57(3): 1423-1430. DOI: 10.7498/aps.57.1423 |
 2017, Vol. 49
2017, Vol. 49


