2. 高速铁路线路工程教育部重点实验室 (西南交通大学),成都 610031;
3. 四川建筑职业技术学院 铁道工程系, 成都 610399;
4. 西南科技大学 环境与资源学院,四川 绵阳 621010
2. Key Laboratory of High-speed Railway Engineering Southwest Jiaotong University, Ministry of Education, Chengdu 610031, China;
3. Department of Railway Engineering, Sichuan College of Architectural Technology, Chengdu 610399, China;
4. School of Environment and Resources, Southwest Science and Technology University, Mianyang 621010, Sichuan, China
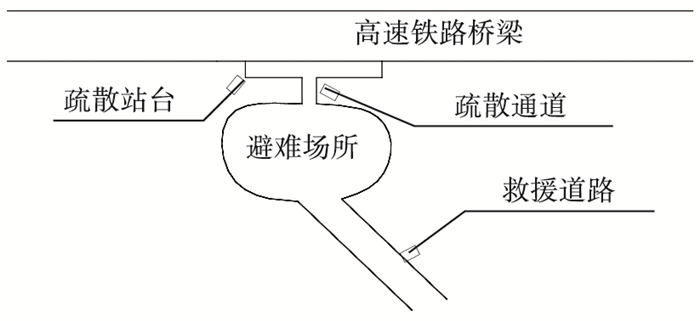
平原区高速铁路工程常以长大桥梁的形式呈现.当桥长超过3 km时,应结合地面道路条件,每隔3 km (单侧6 km) 左右,在线路两侧交错设置一处可上下桥的救援疏散通道[1].但是以上规定在实施时存在一些问题,具体体现在:1) 该条文没有充分考虑人群在桥面上的安全疏散需求.根据该条文,乘客的逃生路径为:列车车厢→高速线路 (或检修通道)→救援疏散通道→地面.然而,高速线路环境复杂,电气设备多,检修通道狭窄,均不利于安全疏散.2) 该条文没有充分考虑人群在地面上的安全避难需求.我国高速列车采用8节编组时,定员为600~800人,如果这些人员全部疏散到地面,若地面不具备容纳大规模人群避难的条件,将会造成不良影响.3) 该条文仅考虑了长大桥梁的救援疏散问题,没有考虑隧道群区段内桥梁的救援疏散问题.隧道群区段的桥梁虽然较短,但如果列车在隧道内发生紧急事件,极有可能停靠至相邻桥梁上疏散并接受救援[2].综上,对于高速铁路长大桥梁,仅根据该条文设置逃生通道无法很好地服务于救援疏散工作.桥梁救援定点是设置在桥梁上的救援疏散站点,具备紧急疏散、方便避难和利于救援三大功能,主要由定点疏散站台、救援疏散通道、避难场所、救援设施及附属设施等组成 (图 1),为高速铁路长大桥梁设置救援定点是增强桥梁救援疏散能力更为有效的渠道.
|
图 1 长大桥梁救援定点示意 Figure 1 Schematic diagram of long bridge rescue sites |
作为高速铁路上集疏散和救援功能于一体的基础设施,救援定点的建设和规划引起了人们的广泛关注.文献[3]介绍了武广客运专线黄土湾大桥救援定点的设置方案;文献[4]阐述了西成客运专线上桥梁救援定点的设置思路和模式;文献[5]研究了山区高速铁路隧道群间桥梁救援定点的设置模式,提出了隧道群间桥梁救援定点的设置条件;文献[6]研究了隧道内救援定点的设置模式及横通道的设置间距.可见,关于救援定点设置方案及模式的研究成果颇多,而关于长大桥梁救援定点优化布局的研究却鲜有报道.
长大桥梁需要配置的救援定点数量可能不止一座,每座救援定点的备选位置也不止一处,选址决策成为其优化布局需解决的首要问题.桥梁救援定点的选址问题是典型的点覆盖线问题,即通过优化布局使得救援定点合理地覆盖桥梁线路区间,此类问题通常采用约束最优化方法求解[7-8].本文将以设置间距、风险等级和救援时程为约束条件,以各地方救援部门至救援定点的最优时程总和最小为目标,建立长大桥梁救援定点的选址决策模型,以期为高速铁路长大桥梁救援定点的选址问题提供可借鉴的方法.
1 高速铁路长大桥梁救援定点的设置间距设置间距是长大桥梁救援定点选址决策的重要约束条件之一.间距太小,工程不经济;间距太大,则无法全面覆盖线路区间.本文将分别从列车制动距离、列车到达救援定点的时间范围及最不利情况下乘客到达救援定点的时间这3个方面来研究桥梁救援定点的设置间距.
1) 考虑列车制动距离的影响.令列车的制动距离为Lz,考虑以下情况:列车在两救援定点中间发生紧急事故,如果两救援定点的间距大于2Lz,才能保证列车停靠在前方相邻救援定点.根据我国高速列车的制动距离,取Lz=3 km,这样救援定点的设置间距宜大于6 km.
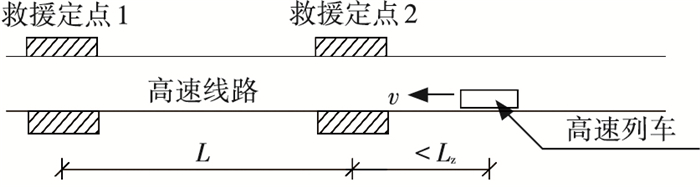
2) 列车到达救援定点的时间范围.令列车制动时间为tz,运行速度为v,两相邻救援定点的间距为L.当列车与前方救援定点的距离刚好为Lz时,如图 2所示,驶至救援定点的时间最短,其值为tz;当距离刚好小于Lz时,有可能驶至下一个救援定点停靠,如图 3所示,行驶时间约为tz+L/v.综上,列车到达救援定点的时间范围为[tz,tz+L/v).取v=250 km/h,tz=1.5 min,计算出救援定点间距为6、10、15、20、25 km 5种情况下,列车到达救援定点的时间分别为[1.5~2.94)、[1.5~3.9)、[1.5~5.1)、[1.5~6.3)、[1.5~7.5) min.列车到达救援定点的容许时间与风险事故的类型有关.考虑多种情况,列车到达救援定点的最长时间以3~5 min为宜.

|
图 2 列车到达救援定点的最短时程图示 Figure 2 Diagram of the least time path train reaching the rescue site |
|
图 3 列车到达救援定点的最长时程图示 Figure 3 Diagram of the longest time path train reaching the rescue site |
3) 最不利情况下乘客到达救援定点的时间.当事故列车被迫紧急制动时,其停靠在线路上的位置具有随机性.这种情况下,乘客必须步行至救援定点疏散并接受救援.当列车停靠在两相邻救援定点中间时,情况最为不利.考虑到桥上线路不平整、疏散通道狭窄等因素,将乘客步行速度取为l m/s.计算出救援定点间距为6、10、15、20、25 km对应的最不利情况下,乘客步行至救援定点的时间分别为50、83.33、125、166.67、208.33 min.对于人们能容忍的最长步行时间,本文对250名在校大学生展开了模拟实验,结果表明:在确保人身安全的前提下,人们在线路上步行的时间不应超过1.5 h,故救援定点的间距不宜超过10 km.综上,对长大桥梁救援定点的设置间距给出以下建议:当区间桥梁长度大于10 km时,应该沿桥梁方向每隔约6~10 km设置一处救援定点.
2 基于贝叶斯网络的救援定点风险概率评估高速铁路长大桥梁救援定点选址决策时,还需考虑备选位置的风险概率等级,以确保救援定点安全可靠.风险概率评估的常用方法有事件树/故障树法、二元决策图法和贝叶斯网络法等[9-11].贝叶斯网络操作简单、建模能力强,本文拟采用贝叶斯网络理论进行救援定点备选位置的风险概率评估.
2.1 建立贝叶斯网络将救援定点设置时应避开的结构致损型风险分为4类:1) 地质灾害风险,记为E1;2) 火灾风险,记为E2;3) 洪水风险,记为E3;4) 车船碰撞风险,记为E4.这4类风险的子风险集记为F,其中F1、F2、F3、F4、F5、F6、F7分别为滑坡风险、泥石流风险、崩塌风险、桥下可燃物火灾风险、洪水风险、车辆碰撞风险、船只碰撞风险.令救援定点备选位置的综合风险为T,基于层次分析法建立救援定点备选位置的风险因素图,见图 4.

|
图 4 救援定点备选位置的风险因素 Figure 4 Risk factors of the alternative rescue sites |
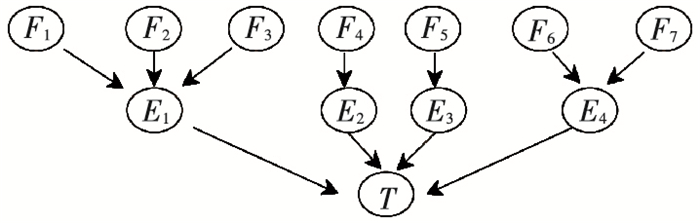
以图 4中底层子风险为根节点,顶层的综合风险为叶节点,建立风险概率评估的贝叶斯网络,见图 5.
|
图 5 救援定点备选位置风险的贝叶斯网络 Figure 5 Bayesian network about risk factors of the alternative rescue sites |
将风险概率分为A、B、C、D 4级,各等级风险的具体情况描述为:A级为风险事件几乎不会发生;B级为风险事件虽有可能发生,但发生可能性很小;C级为风险事件偶尔会发生;D级为风险事件一直在有规律地发生.
根据图 4制作一份救援定点备选位置风险等级调查表,对贝叶斯网络根节点的先验概率等级分布展开调研与问卷.将参与问卷调研的专家级别分为1、2、3级:1级为桥梁工程领域资深专家、高级职称的桥隧段工作人员以及工龄超过20 a的客运段工作人员;2级为中级职称的桥隧段工作人员、工龄10~20 a的客运段工作人员、高级职称的设计及科研人员;3级为初级职称的桥隧段工作人员、工龄5~10 a的客运段工作人员、中级职称的设计及科研人员.以上3级专家的系数分别为1、0.9、0.8.
2.3 计算各节点的风险概率等级根据收集到的问卷资料,即可计算出根节点的概率等级分布,计算公式为
| $P\left( {{F}_{i}}=j \right)=\sum\limits_{k=1}^{n}{{{w}_{k}}{{P}_{ijk}}/\sum\limits_{k=1}^{n}{w_k}}.$ | (1) |
式中:P(Fi=j) 表示风险因素Fi处于等级j的概率,i=1, 2, …, 7,j=A, B, C, D;n为收集到的问卷数 (即专家数);wk为第k个专家的权重;Pijk为第k个专家认为风险因素Fi处于等级j的概率,Pijk=0或1.
子节点条件概率的计算规则为链式传递规则,即如果某父节点的等级为r,而其他父节点的等级不高于r,那么认为子节点等级为r.在本文中,等级A、B、C、D依次增高.以P(E1|F1, F2, F3) 为例说明该问题:
P(E1=A|F1=A, F2=A, F3=A)=1,
P(E1=B|F1=B, F2不高于B, F3不高于B)=1,
P(E1=C|F1=C, F2不高于C, F3不高于C)=1,
P(E1=D|F1=D, F2为任意等级, F3为任意等级)=1,
…
P(E1=C|F1不高于C, F2不高于C, F3=C)=1,
P(E1=D|F1为任意等级, F2为任意等级, F3=D)=1,
P(E1=r|F1高于r, F2为任意等级, F3为任意等级)=0,
P(E1=r|F1为任意等级, F2高于r, F3为任意等级)=0,
P(E1=r|F1为任意等级, F2为任意等级, F3高于r)=0.
将根节点概率等级分布输入到图 5所示的贝叶斯网络中,根据以上链式传递规则,可推算出非根节点的概率等级分布.然后,基于最大隶属度原则确定救援定点备选位置的风险概率等级.
由于桥梁救援定点的安全性事关重大,本文建议,如果救援定点备选位置的风险概率为C级或D级时,就应舍弃该备选位置或采取风险防治措施.
3 考虑救援时程的救援定点选址决策桥梁救援定点还应满足交通便捷、就近救援的要求.各救援部门的车辆沿着最优路径行驶至救援定点的时间 (即救援时程),应小于1 h.为便于评价,需寻求各救援部门至救援定点的最优路径.鉴于Dijkstra算法是求解一点到其余各点之间最短路径的最为经典的算法[12-13],本文拟采用该算法求解.具体步骤如下:1) 绘制救援定点与各救援部门 (包括消防部门、医疗部门、地方铁路管理机构、地方救援指挥中心等) 之间的救援道路网络图.连接各救援部门与救援定点的道路应直捷、顺畅,符合消防车道的标准.2) 将实际路网抽象为有向带权网络.以救援定点为源点,以道路交叉口为节点,以救援车辆在道路上的运行时间为权值,构建网络模型.道路权值应考虑路径长度、设计车速、道路畅通概率等因素,计算公式为t=60l/(η·v).式中t为车辆在研究路段上运行的时间,min;l为研究路段的长度,km;η为研究路段的畅通率,取早晚高峰时段的统计数值;v为研究路段的设计车速,km/h.3) 应用Dijkstra算法寻求救援定点与各救援部门之间时程最短的路径,并将最优路径还原到实际路网中.
若求得的救援时程超过1 h,可采取以下两种措施:1) 淘汰该救援定点备选位置;2) 优化救援定点附近的路况,以缩短救援时程.
4 长大桥梁救援定点的选址决策模型令α为拟设救援定点的备选位置数目;β为地方救援部门的数目;tλ(x) 为第λ个救援部门与第x个备选位置之间的救援时程,min;d(x) 为第x个备选位置与前一个救援定点的间距,km;P(x) 为第x个备选位置的结构致损型风险等级;Y为各地方救援部门至救援定点备选位置的时程总和.其中,x=1, 2, …, α;λ=1, 2, …, β;P(x)=A, B, C, D.
以设置间距、风险等级和救援时程为约束条件,以各地方救援部门至救援定点的最优时程总和最小为目标,建立长大桥梁救援定点的选址决策模型为
| $\min \ Y=\sum\limits_{\lambda =1}^{\beta }{{{t}_{\lambda }}\left( x \right)}, $ | (1) |
| $\text{s}\text{.t}\text{.}\left\{ \begin{matrix} 6\le d\left( x \right)\le 10, \\ {{t}_{\lambda }}\left( x \right)\le 60, \\ P\left( x \right)=\text{A或B}\text{.} \\ \end{matrix} \right.$ |
由于长大桥梁拟设的救援定点数量及备选位置有限,且约束条件简洁直观,建议采用枚举法和筛选法求解模型,沿桥梁线路方向依次进行救援定点的决策定位.
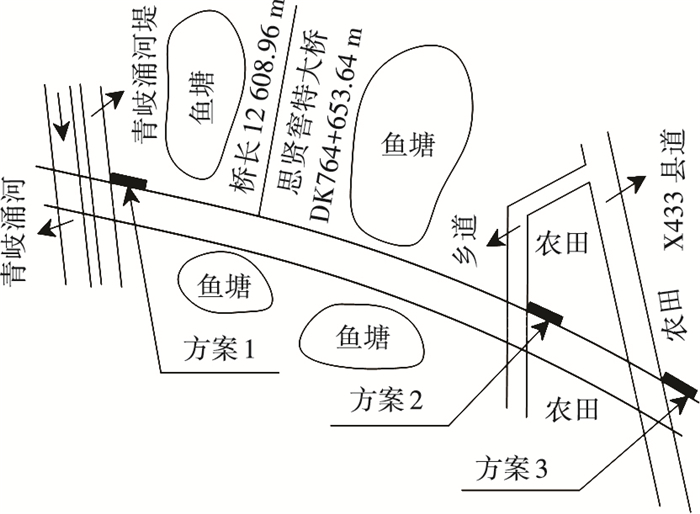
5 工程实例贵广高铁思贤窖特大桥全桥长12 608.96 m,位于佛山市三水区,主要跨越青歧涌河和思贤窖河.沿线穿越的主要道路有X433县道、X503县道、青歧涌河堤、思贤窖河堤及若干乡村道路.根据设置间距要求,该桥梁只需设置1座救援定点.通过实地调研,得到救援定点的3个选址方案,如图 6所示.
|
图 6 思贤窖大桥救援定点的选址方案 Figure 6 Location decisions of the rescue sites on Sixianjiao bridge |
方案1:桩号DK764+240.00处,紧邻青岐涌河堤;
方案2:桩号DK765+500.00处,紧邻某乡村道路;
方案3:桩号DK765+900.00处,紧邻X433县道.
首先对这3个备选位置进行风险评估.针对图 4所示的风险因素,向20位专家发放了问卷调查表.其中,1级专家3位,2级专家12位,3级专家5位.根据问卷结果,利用式 (1) 计算得到救援定点备选位置的风险概率等级分布表,见表 1.
| 表 1 救援定点选址方案的风险分级概率 Table 1 Risk grading probability of the alternative rescue sites |
从表 1可知,3个方案的风险概率等级均为B,满足约束条件.接下来,根据救援时程进行方案筛选.位置1紧邻的青岐涌河堤为等外级道路,宽4 m;位置2紧邻的乡道为等外级道路,宽4 m;位置3紧邻的X433县道为三级公路,宽7 m.采用Dijkstra算法,得到3个备选位置与佛山市三水区各救援部门的最优时程,见表 2.
| 表 2 地方救援部门至救援定点的最优时程 Table 2 Least time-histories between local rescue departments and rescue sites |
根据式 (2),方案1不满足救援时程的约束条件;对于方案2和方案3,4个地方救援部门至救援定点的最短时程总和分别为220、187 min,故方案3为最优方案.由此,思贤窖大桥的救援定点位置最终选定在DK765+900.00处,如图 7所示.

|
图 7 思贤窖特大桥救援定点的设置位置 Figure 7 Rescue sites locating on Sixianjiao extra large bridge |
1) 以设置间距、风险等级和救援时程为约束条件,以各地方救援部门至救援定点的最优时程总和最小为目标,建立了选址决策模型,为长大桥梁救援定点的选址决策问题提供了行之有效的方法.
2) 研究了救援定点选址决策的3个约束条件,得到以下结论:当区间桥梁长度大于10 km时,应该沿桥梁线路方向每隔约6~10 km设置一处救援定点;备选位置的风险概率应为A级或B级;地方救援部门的车辆沿最优路径行驶至救援定点的时程应短于1 h.
3) 以贵广高铁思贤窖特大桥的救援定点选址决策为例,阐述了模型的具体应用,结果表明该模型很好地解决了长大桥梁救援定点的选址决策问题.
| [1] |
高速铁路设计规范: TB 10621—2014[S]. 北京: 中国铁道出版社, 2014.
Code for Design of High Speed Railway: TB 10621—2014[S].Beijing: China Railway Publishing House, 2014. |
| [2] | TAKITA T. Research on prevention of train fire[J]. Rail International, 1977, 8(7): 395-406. |
| [3] |
颜志伟. 武广客运专线大瑶山隧道群防灾救援疏散设计研究[J].
铁道工程学报, 2011(8): 7-12.
YAN Zhiwei. Study on design of disaster prevention and rescue evacuation system for Dayaoshan tunnel group of Wuhan—Guangzhou passenger dedicated line[J]. Journal of Railway Engineering Society, 2011(8): 7-12. |
| [4] |
史先伟. 山区客运专线的防灾救援及安全疏散方案[J].
铁道标准设计, 2011(8): 75-79.
SHI Xianwei. Harzard prevention and rescue options for mountainous passenger-dedicated railways[J]. Railway Standard Design, 2011(8): 75-79. DOI: 10.13238/j.issn.1004-2954.2011.08.001 |
| [5] |
项琴, 李远富, 葛根荣. 高速铁路隧道群内桥梁救援定点的设置方法研究[J].
中国安全科学学报, 2014, 24(6): 99-104.
XIANG Qin, LI Yuanfu, GE Genrong. Research on allocation method of emergency station on high speed railway bridge in tunnel group[J]. China Safety Science Journal, 2014, 24(6): 99-104. DOI: 10.16265/j.cnki.issn1003-3033.2014.06.028 |
| [6] |
张念. 高海拔特长铁路隧道火灾燃烧特性与安全疏散研究[D]. 北京: 北京交通大学, 2012.
ZHANG Nian.Research on combustion characteristics and safety evacuation of high-altitude super-long railway tunnel[D].Beijing: Beijing Jiaotong University, 2012. |
| [7] | HAKIMI S L. Optimum distribution of switching centers in a communication network and some related graph theoretic problems[J]. Operations Research, 1965(13): 462-475. |
| [8] | KIM J, KWON H D, LEE J. Constrained optimal control applied to vaccination for influenza[J]. Computers and Mathematics with Applications, 2016, 71(11): 2313-2329. DOI: 10.1016/j.camwa.2015.12.044 |
| [9] | DAVID M, MARTIN N, NORMAN F. Improved reliability modeling using Bayesian networks and dynamic discretization[J]. Reliability Engineering and System Safety, 2010, 95(4): 412-425. DOI: 10.1016/j.ress.2009.11.012 |
| [10] | BOUDALI H, DUGAN J B.A discrete-time Bayesian network reliability modeling and analysis framework[J]. Reliability Engineering and System Safety, 2005, 87(3): 337-349[J]. Reliability Engineering and System Safety, 2005, 87(3): 337-349. DOI: 10.1016/j.ress.2004.06.004 |
| [11] |
赵英, 郭亮. 贝叶斯方法的污染源季节性排放量控制和管理[J].
哈尔滨工业大学学报, 2014, 46(12): 26-32.
ZHAO Ying, GUO Liang. A seasonal management method for controlling pollution sources discharge based on Bayesian method[J]. Journal of Harbin Institute of Technology, 2014, 46(12): 26-32. DOI: 10.11918/j.issn.0367-6234.2014.12.005 |
| [12] | DIJKSTRA E W. A note on two problems in connection with graphs[J]. Numerische Mathematik, 1959(1): 269-271. |
| [13] |
王志坚, 韩伟一, 李一军. 具有多条最短路径的最短路问题[J].
哈尔滨工业大学学报, 2010, 42(9): 1428-1431.
WANG Zhijian, HAN Weiyi, LI Yijun. Shortest path problem with multiple shortest paths[J]. Journal of Harbin Institute of Technology, 2010, 42(9): 1428-1431. DOI: 10.11918/j.issn.0367-6234.2010.09.017 |
 2017, Vol. 49
2017, Vol. 49


