2. 土木工程防灾国家重点实验室 (同济大学),上海 200092
2. State Key Laboratory of Disaster Reduction in Civil Engineering (Tongji University), Shanghai 200092, China
П型开口主梁由型钢和混凝土组成,能够充分发挥两种材料的优势,且受力合理、施工方便,在斜拉桥中得到广泛应用[1].中国的上海南浦大桥、杨浦大桥、青州闽江大桥和加拿大Annacis桥等均采用П型开口主梁断面.与流线型闭口箱型主梁断面相比,П型断面属于典型的钝体断面,其抗扭刚度相对较小,且气动力对其外形非常敏感.颤振、涡振和抖振是大跨度桥梁的3种主要振动形式,也是大跨度斜拉桥抗风性能检验的主要指标.其中颤振和涡振是由结构与气流的流固耦合相互作用形成的自激振动[2-3],而抖振属于强迫振动.对于一般跨度的斜拉桥,通常仅通过节段模型风洞试验对其抗风稳定性进行检验和评估.节段模型风洞试验可以对主梁的颤振和涡振性能进行直接检验,但是对于抖振,则只能获得气动力参数,还需要通过计算获得抖振位移响应特征值后才能对其抖振性能进行评估.虽然全桥气弹模型风洞试验可以同时实现颤振、涡振和抖振的直接检验,但是该类试验难度大、成本高,仅对跨度特别大、重要等级特别高或者结构造型特别复杂的斜拉桥才进行补充检验.鉴于П型开口主梁钝体断面空气扰流问题的复杂性,目前主要借助于节段模型风洞试验对其抗风性能进行检验和评估.本文以某主跨300 m的两塔三跨双索面П型主梁断面斜拉桥为工程背景,设计了3种不同的П型开口主梁断面,在风洞试验的基础上采用同时考虑自激力和抖振力的计算模型对其抖振响应进行分析,并从抖振抗风性能的角度进行П型主梁断面气动比选研究.
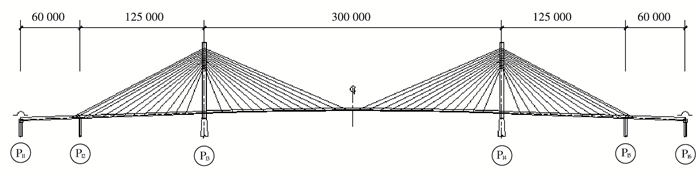
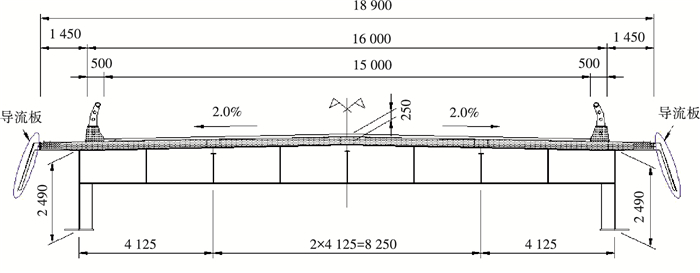
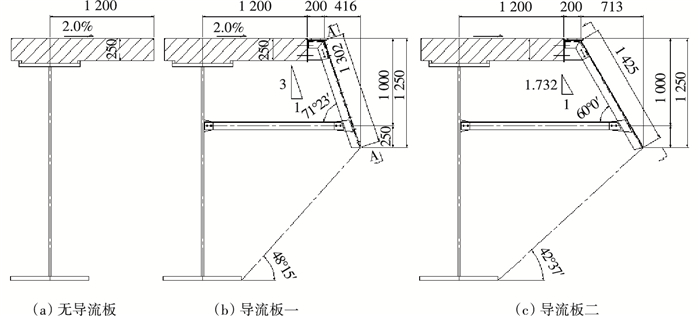
1 工程概况和结构动力特性分析文献[4]以节段模型风洞试验为基础,从颤振和涡振的角度进行了П型主梁断面气动选型研究.本文将从抖振的角度对其气动性能进行评估.文献[4-5]给出了本文斜拉桥的详细资料,为便于理解,此处简要给出斜拉桥的主要参数.斜拉桥跨径组合为60 m+125 m+300 m+125 m+60 m=670 m,结构布置如图 1所示;主梁采用型钢-混凝土П型开口断面,主结构宽18.900 m,中心梁高2.905 m,标准主梁断面如图 2所示;主塔采用混凝土钻石型桥塔,塔高91 m.设计3组主梁断面,分别为无导流板主梁断面、导流板一主梁断面和导流板二主梁断面,如图 3所示.
|
图 1 斜拉桥整体布置 (mm) Figure 1 General layout of the cable-stayed bridge (mm) |
|
图 2 斜拉桥标准主梁断面 (mm) Figure 2 Cross section of the standard main girder of the cable-stayed bridge (mm) |
|
图 3 标准主梁断面导流板 (mm) Figure 3 Wind fairings of cross section of the standard main girder (mm) |
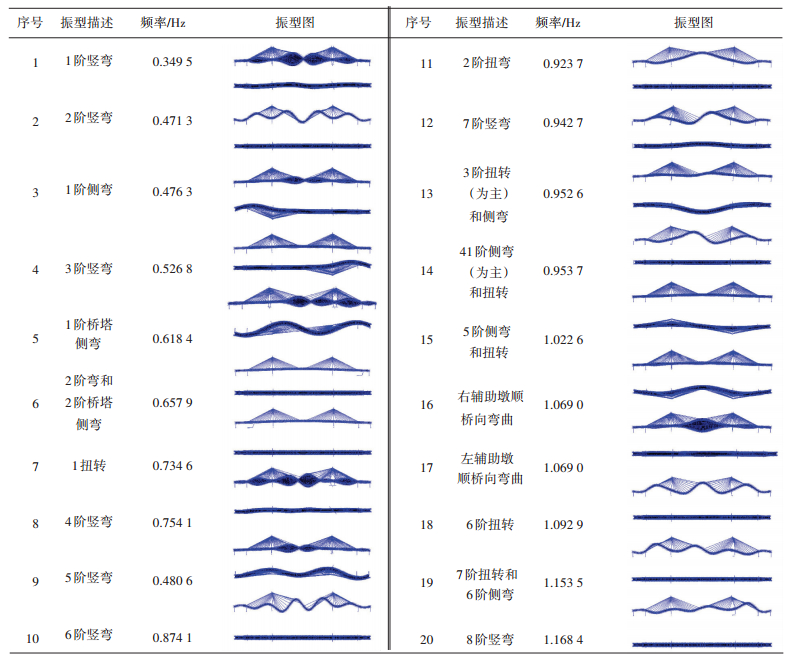
采用离散结构的有限单元法建立斜拉桥有限元模型,如图 4所示.本文采用ANSYS有限元程序,斜拉桥有限元模型中各参数和单元的设置详见文献[4-5].经模态分析,得成桥阶段斜拉桥主梁前20阶振型和频率见表 1.
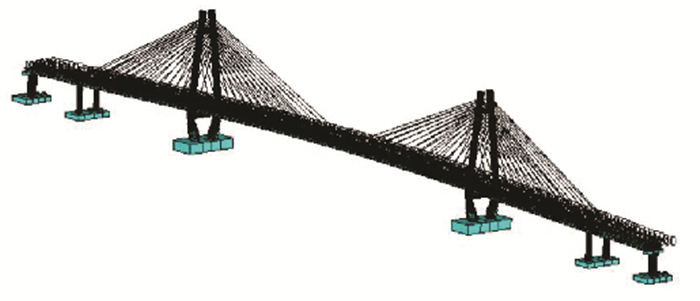
|
图 4 斜拉桥结构有限元模型 Figure 4 Finite element model of the cable-stayed bridge |
| 表 1 斜拉桥前20阶振型和频率 Table 1 The top 20 mode shapes and frequencies of the cable-stayed bridge |
主梁断面的颤振导数、静力三分力系数及其变化率等参数是桥梁风振计算的主要参数,为此设计制作了缩尺比为1:35的主梁节段模型,通过风洞试验对其气动力参数进行识别.主梁节段模型风洞试验在同济大学土木工程防灾国家重点实验室TJ-1大气边界层风洞中进行,节段模型测振风洞试验在风洞中的布置如图 5所示.通过节段模型测振风洞试验获得不同主梁断面在不同风攻角时的颤振导数 (A1*~A4*,H1*~H4*). 0°风攻角时的颤振导数如图 6所示,3°和-3°时的颤振导数详见文献[5].

|
图 5 斜拉桥节段模型测振风洞试验 Figure 5 Sectional model vibration wind tunnel test of the cable-stayed bridge |
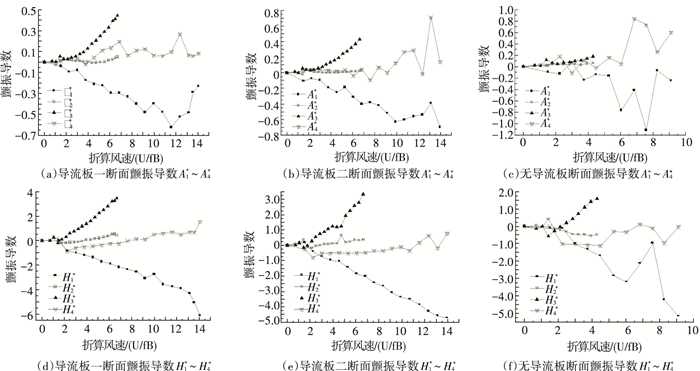
|
图 6 0°风攻角时标准主梁断面的颤振导数 Figure 6 Flutter derivatives of the standard girder cross section under 0° wind attack angle |
进行节段模型测力风洞试验,模型在风洞中的布置如图 7所示.通过节段模型测力风洞试验分别获得标准主梁断面的静力三分力系数如图 8所示.标准主梁断面阻力系数CD、升力系数CL、升力矩系数CM定义为
| ${{C}_{\text{D}}}=\frac{{\bar{D}}}{\frac{1}{2}\rho {{U}^{2}}H}, {{C}_{\text{L}}}=\frac{{\bar{L}}}{\frac{1}{2}\rho {{U}^{2}}B}, {{C}_{\text{M}}}=\frac{{\bar{M}}}{\frac{1}{2}\rho {{U}^{2}}{{B}^{2}}}.$ |
式中:D、L、M分别指标准主梁断面在体轴坐标系下的阻力、升力和升力矩,对应的3个方向的位移响应分别为p、h、α(正方向规定见图 9);上标“-”表示平均风荷载;U为来流方向的平均风速;ρ为空气密度,ρ=1.225 kg/m3;B、H分别为计算中所采用的标准主梁断面的宽度和高度.

|
图 7 斜拉桥节段模型测力风洞试验 Figure 7 Sectional model force balance wind tunnel test of the cable-stayed bridge |
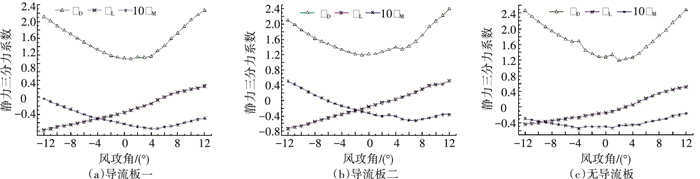
|
图 8 标准主梁断面静力三分力系数 Figure 8 Three-component static wind loading coefficients of the standard girder cross section |
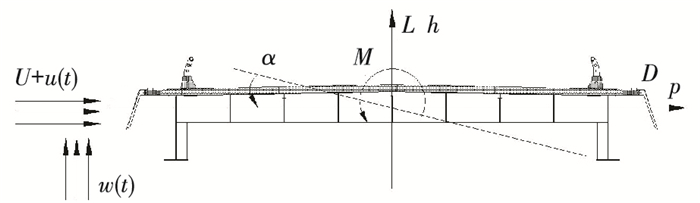
|
图 9 标准主梁断面三分力方向示意图 Figure 9 Positive directions of three-component wind loading of the standard girder cross section |
抖振属于限幅随机振动,主要对斜拉桥主梁运营阶段的位移和疲劳产生影响,故本文中的主梁抖振响应比较仅考虑成桥阶段.斜拉桥抖振计算中同时考虑作用在主梁上的抖振力、自激力和平均风荷载.其中,平均风荷载处理为静力荷载,可以通过三分力系数很方便的表达.本文计算中抖振力采用Davenport计算模型[6],其表达式为
| $\left\{ \begin{align} &{{D}_{\text{b}}}=\frac{1}{2}\rho {{U}^{2}}B\left[2{{C}_{\text{D}}}{{\chi }_{\text{Du}}}\frac{u\left( t \right)}{U}+{{{{C}'}}_{\text{D}}}{{\xi }_{\text{Dw}}}\frac{w\left( t \right)}{U} \right], \\ &{{L}_{\text{b}}}=\frac{1}{2}\rho {{U}^{2}}B\left[2{{C}_{\text{L}}}{{\xi }_{\text{Lu}}}\frac{u\left( t \right)}{U}+\left( {{{{C}'}}_{\text{L}}}+{{C}_{\text{D}}} \right){{\xi }_{\text{Lw}}}\frac{w\left( t \right)}{U} \right], \\ &{{M}_{\text{b}}}=\frac{1}{2}\rho {{U}^{2}}{{B}^{2}}\left[2{{C}_{\text{M}}}{{\chi }_{\text{Mu}}}\frac{u\left( t \right)}{U}+{{{{C}'}}_{\text{M}}}{{\chi }_{\text{Mw}}}\frac{w\left( t \right)}{U} \right]. \\ \end{align} \right.$ |
式中:下标b表示抖振力;
受客观条件所限,该桥未能进行主梁气动导纳识别风洞试验,抖振计算中采用Sears函数的Liepmann简化表达式[7].
自激力采用考虑18个颤振导数的Scanlan计算模型[8],其表达式为
| $\left\{ \begin{align} &{{D}_{\text{ae}}}=\frac{1}{2}\rho {{U}^{2}}\left( 2B \right)\left( KP_{1}^{*}\frac{{\dot{p}}}{U}+KP_{2}^{*}\frac{B\dot{\alpha }}{U}+{{K}^{2}}P_{3}^{*}\alpha + \right. \\ &\left. \ \ \ \ \ \ \ \ {{K}^{2}}P_{4}^{*}\frac{p}{B}+KP_{5}^{*}\frac{{\dot{h}}}{U}+{{K}^{2}}P_{6}^{*}\frac{h}{B} \right), \\ &{{L}_{\text{ae}}}=\frac{1}{2}\rho {{U}^{2}}\left( 2B \right)\left( KH_{1}^{*}\frac{{\dot{h}}}{U}+KH_{2}^{*}\frac{B\dot{\alpha }}{U}+{{K}^{2}}H_{3}^{*}\alpha \right.+ \\ &\ \ \ \ \ \ \ \left. {{K}^{2}}H_{4}^{*}\frac{h}{B}+KH_{5}^{*}\frac{{\dot{p}}}{U}+{{K}^{2}}H_{6}^{*}\frac{p}{B} \right), \\ &{{M}_{\text{ae}}}=\frac{1}{2}\rho {{U}^{2}}\left( 2{{B}^{2}} \right)\left( KA_{1}^{*}\frac{{\dot{h}}}{U}+KA_{2}^{*}\frac{B\dot{\alpha }}{U}+{{K}^{2}}A_{3}^{*}\alpha \right.+ \\ &\ \ \ \ \ \ \ \ \left. {{K}^{2}}A_{4}^{*}\frac{h}{B}+KA_{5}^{*}\frac{{\dot{p}}}{U}+{{K}^{2}}A_{6}^{*}\frac{p}{B} \right). \\ \end{align} \right.$ |
式中:下标ae表示自激力;
抖振计算中同时考虑水平和竖向的脉动风作用,其脉动风谱Suu、Sww分别采用Kaima谱[10]和Lumley-Panofsky修正风谱[11],表达式为
| $\left\{ \begin{align} &{{S}_{uu}}\left( n \right)=\frac{u_{*}^{2}}{n}\cdot \frac{200f}{{{\left( 1+50f \right)}^{5/3}}}, \\ &{{S}_{ww}}\left( n \right)=\frac{u_{*}^{2}}{n}\cdot \frac{3.36f}{1+10{{f}^{5/3}}}. \\ \end{align} \right.$ |
式中:U(z) 为高度z处的平均风速,m/s;z为离地面或水面的高度,m;n为脉动风的频率,Hz;
水平和竖向脉动风的交叉风谱仅考虑余谱Cuw的作用,计算中采用适合工程应用的经验表达式为
| ${{C}_{\text{uw}}}\left( n \right)=\frac{u_{*}^{2}}{n}\cdot \frac{14f}{1+9.6{{f}^{2.4}}}.$ |
脉动风的空间相关性采用公路桥梁抗风设计规范[12]建议的形式,计算中风场相关系数偏安全地取为7.根据文献[5],本文中斜拉桥桥位处的地表粗糙度类型为A类,地面粗糙长度z0=0.01 m,平均风剖面指数为0.12;主梁离水面的高度约为30 m,斜拉桥成桥阶段100 a重现期主梁高度处的设计基准风速为37.65 m/s.当考虑结构前20阶振型,使用同时考虑自激力和抖振力的耦合抖振计算方法[13-15],采用上述参数计算不同П型主梁断面斜拉桥的抖振位移响应极值包络如图 10所示.其中,位移响应极值计算公式为
| $\hat{y}=\bar{y}\pm g\cdot {{\sigma }_{y}}.$ |
式中:y为位移响应,分别代表p、h、α;为抖振位移响应极大值或极小值,为平均风荷载引起的位移响应;g为峰值因子,通常情况下可取为3.5;σy为抖振位移响应的根方差.
观察图 10可以发现,在风攻角、风环境和计算方法完全相同的情况下,不同П型主梁断面产生的抖振位移响应极值包络图的形状基本相同,但数值却存在不小区别.上述现象表明,通过改变主梁外形可以改变斜拉桥主梁的抖振位移响应.
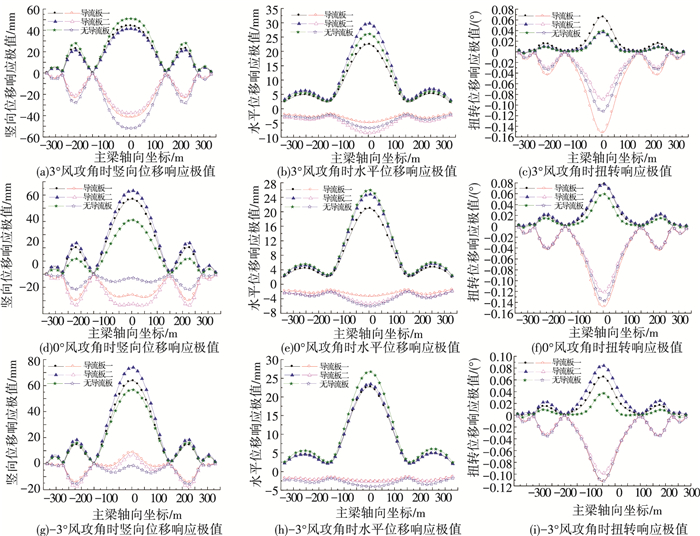
|
图 10 斜拉桥主梁抖振位移响应极值包络图 Figure 10 Buffeting displacement envelope of the main girder of cable-stayed bridge |
为定量比较不同形状П型主梁断面对斜拉桥抖振位移响应的影响,取主梁关键节点处的响应值进行分析,见表 2.本文中的关键点取主跨跨中、主跨1/4跨和边跨跨中.考虑到结构左右对称,表 2仅给出了主跨左侧1/4跨和左侧边跨跨中处的抖振位移响应.由于抖振引起的是动力随机响应,表 2中各工况的计算值取关键点处抖振位移响应包络值中的绝对最大值,为便于分析,该值全部取绝对值.
| 表 2 斜拉桥主梁抖振位移响应比较 Table 2 Buffeting displacement comparison of the main girder of cable-stayed bridge |
对于竖向抖振位移响应,最大值均发生在主跨跨中处.在3个风攻角中,-3°为竖向抖振位移响应的最不利工况,导流板一、导流板二和无导流板断面的响应最大值分别为0.063 7、0.073 9、0.056 8 m. 3°风攻角时,无导流板断面的响应值最大,导流板一断面和导流板二断面在主跨跨中处分别比无导流板断面小13.0%和18.4%;0°风攻角时,无导流板断面的响应最小,导流板一和导流板二断面在主跨跨中处分别比无导流板断面大38.3%和54.2%;-3°风攻角时,无导流板断面的响应最小,导流板一断面和导流板二断面在主跨跨中处分别比无导流板断面大12.2%和30.2%.比较分析发现,如果仅考虑竖向抖振位移响应,无导流板断面相对最好,导流板一断面次之,导流板二断面相对最差.
对于水平抖振位移响应,最大值均发生在主跨跨中处.对于导流板一断面,最大水平抖振位移响应为0.022 7 m,发生在-3°风攻角时;对于导流板二断面,最大水平抖振位移响应为0.029 8 m,发生在3°风攻角时;对于无导流板断面,最大水平抖振位移响应为0.026 8 m,发生在-3°风攻角时. 3°风攻角时,导流板二断面的响应值最大,导流板一断面的响应最小,分别是无导流板断面响应的114%和86%;0°风攻角时,无导流板断面的响应最大,导流板一断面和导流板二断面在主跨跨中处分别比无导流板断面小19.5%和4.3%;-3°风攻角时,同样是无导流板断面的响应最大,导流板一断面和导流板二断面在主跨跨中处分别比无导流板断面小15.2%和12.4%.由表 2和图 12可以发现,水平抖振位移响应在主跨1/4跨和边跨跨中处存在与主跨跨中相似的规律.如果仅考虑水平抖振位移响应,导流板一断面相对最好,无导流板断面次之,导流板二断面相对最差.
对于扭转抖振位移响应,最大值同样均发生在主跨跨中处.对于导流板一断面,最大扭转抖振位移响应为0.152 1°,发生在3°风攻角时;对于导流板二断面,最大扭转抖振位移响应为0.121 5°,发生在0°风攻角时;对于无导流板断面,最大扭转抖振位移响应为0.137 5°,发生在0°风攻角时. 3种不同的风攻角工况下,导流板一断面的扭转响应值均最大,导流板二断面的均最小.主跨跨中位置处,3°、0°、-3°风攻角时导流板一和导流板二断面的扭转抖振响应分别是无导流板断面的136.1%和79.8%,108.1%和88.4%,100.4%和88.1%;主跨1/4跨位置处,3°、0°、-3°风攻角时导流板一和导流板二断面的扭转抖振响应分别是无导流板断面的138.4%和81.9%,111.2%和95.9%,100.0%和95.1%;边跨跨中位置处,3°、0°、-3°风攻角时导流板一和导流板二断面的扭转抖振响应分别是无导流板断面的128.5%和80.4%,104.4%和95.8%,94.6%和91.2%.比较发现,如果仅考虑扭转抖振位移响应,导流板二断面相对最好,无导流板断面次之,导流板一断面相对最差.
4 结论1) 实例分析表明,通过改变П型开口主梁断面的外形,可以改变主梁任一自由度上的抖振响应.
2)П型开口主梁断面外形的改变,对斜拉桥各自由的抖振响应的影响不同.与无导流板断面相比,增加导流板一可以改善水平方向的抖振性能,却使得其他两个自由度方向上的抖振性能恶化;增加导流板二可以改善扭转方向的抖振性能,同时使其它两个方向的抖振性能恶化.外形改变对主梁竖向、侧向和扭转抖振的影响很难同时达到最优.
3) 斜拉桥主梁的竖向荷载通常由车辆荷载和结构自重控制,水平荷载通常由风荷载控制.抖振比选分析中应将竖向作为次要因素,侧向作为主要因素,扭转介于两者之间.
4) 与颤振和涡振相比,抖振在大跨度斜拉桥抗风设计中通常不起控制作用.基于斜拉桥的受力特点,综合考虑斜拉桥颤振、涡振和抖振性能,对于本文中的斜拉桥建议优先选用导流板二断面.
| [1] |
宋锦忠, 哈鸿, 毛鸿银. 开口主梁断面的气动选型[C]//第五届全国风工程及工业空气动力学学术会议论文集. 张家界: 中国空气动力学会风工程和工业空气动力学专业委员会, 1998: 240-245.
SONG Jinzhong, HA Hong, MAO Hongyin.Aerodynamic selection of open bridge deck[C]// Proceeding of the 5th national conference on wind engineering and industrial aerodynamics.Zhangjiajie: China Aerodynamics and Industrial Aerodynamics Specialized Committee, 1998: 240-245. |
| [2] |
刘祖军, 杨詠昕. H形桥梁断面颤振的流场驱动机理及气流能量分析[J].
土木工程学报, 2013, 46(4): 110-116.
LIU Zujun, YANG Yongxin. Flow field mechanism and air energy characteristic of H-shape section in flutter[J]. China Civil Engineering Journal, 2013, 46(4): 110-116. |
| [3] |
刘祖军, 贾明晓, 杨詠昕. 平板断面风致振动的流场驱动机理分析[J].
中国公路学报, 2012, 25(4): 75-82.
LIU Zujun, JIA Mingxiao, YANG Yongxin. Flow field mechanism of flutter of plate section[J]. China Journal of Highway and Transport, 2012, 25(4): 75-82. |
| [4] |
董锐, 杨詠昕, 葛耀君. 斜拉桥Π型开口断面主梁气动选型风洞试验[J].
哈尔滨工业大学学报, 2012, 44(10): 109-114.
DONG Rui, YANG Yongxin, GE Yaojun. Wind tunnel test for aerodynamic selection of Ⅱ shaped deck of cable-stayed bridge[J]. Journal of Harbin Instituted of Technology, 2012, 44(10): 109-114. DOI: 10.11918/j.issn.0367-6234.2012.10.023 |
| [5] | YANG Yongxin, DONG Rui.Wind tunnel study on wind-resistant performance of Co Chien cable-stayed bridge in Vietnam (Research Report)[R].Shanghai: State Key Laboratory of Disaster Reduction in Civil Engineering (Tongji University), 2011. |
| [6] | DAVENPORT A G. Buffeting of a suspension bridge by storm winds[J]. Journal of the Structural Division-ASCE, 1962, 88(3): 233-70. |
| [7] | LIEPMANN H W. On the application of statistical concepts to the buffeting problem[J]. Journal of Aeronautical Science, 1952, 19(12): 793-800. DOI: 10.2514/8.2491 |
| [8] | SCANLAN R H. The action of flexible bridges under wind, Ⅰ: flutter theory[J]. Journal of Sound and Vibration, 1978, 60(2): 187-99. DOI: 10.1016/S0022-460X(78)80028-5 |
| [9] | CHEN X Z, MATSUMOTO M, KAREEM A. Aerodynamic coupling effects on flutter and buffeting of bridges[J]. Journal of Engineering Mechanics-ASCE, 2000, 126(1): 17-26. DOI: 10.1061/(ASCE)0733-9399(2000)126:1(17) |
| [10] | KAIMAL J C, WYNGAARD J C, IZUMI Y, et al. Spectral characteristics of surface-layer turbulence[J]. Quarterly Journal of the Royal Meteorological Society, 1972, 98(417): 563-589. DOI: 10.1002/(ISSN)1477-870X |
| [11] | LUMLEY J L, PANOFSKY H A. The structure of atmospheric turbulence[M]. New York: John Wiley & Sons, Inc., 1964. |
| [12] |
中华人民共和国交通部. 公路桥梁抗风设计规范: JTG/T D60-01-2004 [S]. 北京: 人民交通出版社, 2004.
Ministry of Transport of the People's Republic of China.Wind-resistant design specification for highway bridges: JTG/T D60-01-2004[S].Beijing: China Communications Press, 2004. |
| [13] |
丁泉顺. 大跨度桥梁耦合颤抖振响应的精细化分析[D]. 上海: 同济大学, 2001.
DING Quanshun.Refinement of coupled flutter and buffeting analysis for long-span bridges [D].Shanghai: Tongji University, 2001. |
| [14] | JONES N P, SCANLAN R H. Theory and full-bridge modeling of wind response of cable-supported bridges[J]. Journal of Bridge Engineering, 2001, 6(6): 365-375. DOI: 10.1061/(ASCE)1084-0702(2001)6:6(365) |
| [15] |
董锐. 大跨度桥梁多目标等效静力风荷载研究[D]. 上海: 同济大学, 2014.
DONG Rui.Multi-target equivalent static wind loading of long-span bridges [D].Shanghai:Tongji University, 2014. |
 2017, Vol. 49
2017, Vol. 49