随着航天事业的快速发展，空间技术逐渐从最初的空间利用提升为空间控制^[1]，空间打击、跟踪监视、交会对接等问题的研究越来越受到航天大国的关注和重视，其中对空间非合作目标的接近和近距离跟踪监视问题已经成为当今航天领域的一个非常重要的研究热点.

经典的相对轨道动力学模型中，无论是只适用于近圆轨道的C-W方程还是考虑了轨道偏心率非零情况的Lawden方程^[2-3]，当针对非合作目标时，由于对目标的一些运动参数难以精确测量而无法有效使用.从接近非合作目标时的实际测量情况出发，文献[4-6]提到了一种在以追踪航天器质心为原点的视线坐标系下建立的相对运动模型，具有不限制目标轨道偏心率，解算方程不受目标未知参数影响，可在任意初始位置进行逼近和视线跟踪等优点.文献[5]还综合考虑体坐标系下由相对误差四元数描述的相对姿态方程，从而建立了六自由度的动力学模型.相对轨道与姿态的控制耦合问题主要有两方面原因，一种是由期望控制指令引起的，另一种则是因为推力与姿态有关导致的^[7].对于姿态轨道耦合控制，许多学者都进行了研究，其中文献[8-9]从HJB方程中导出了鲁棒性较好且使用方便的状态依赖黎卡提方程法 (state-dependent riccati equation，SDRE)，可以用来解决一些含有不确定性的鲁棒控制问题，但在线求解黎卡提方程使计算负担增大.文献[5, 10-11]在进行姿轨耦合控制时，以能量消耗以及误差最小为指标，引入中间变量，将SDRE方程转化为迭代方程，有效降低了计算负担，但这种控制方法在非合作目标同时存在轨道和姿态机动时，控制误差较大.值得说明的是，上述研究主要都还是集中在合作目标的情况，而对于接近和跟踪非合作目标的研究则较少.除了普遍存在模型不确定性和外部干扰外，对于追踪航天器，非合作目标的一些运动信息无法精确已知.RBF神经网络对未知非线性函数具有良好的逼近能力^[12]，因此可以对模型不确定性及外部干扰等进行逼近与补偿.目前对于接近并跟踪空间目标的研究大多都是实现控制误差渐近稳定的控制结果，并且理论上系统状态收敛到期望值的时间无穷大.有限时间控制^[12]能够使闭环系统的状态在有限时间内收敛到平衡点，相比于非有限时间的控制方法不仅收敛更快，而且具有更好的鲁棒性.许多有限时间控制方法采用反步法的思想来设计控制律^[13]，使用递推的设计，使许多复杂、高阶非线性系统的控制律设计变得简便.对于实际的航天器控制，一定存在控制输入饱和、死区等非线性特性^[14-15]，因此在进行姿态、轨道控制律设计时有必要考虑这些非线性特性对系统的影响.

本文针对非合作目标存在姿态翻滚以及未知轨道机动时，追踪航天器对其保持近距离跟踪与指向的问题，建立了姿态与轨道同步控制模型.考虑到系统不确定性、非合作目标运动参数部分未知等情况，利用RBF神经网络方法进行自适应估计和补偿，采用反步法思想设计控制律使追踪航天器在有限时间内收敛到期望的相对轨道和姿态.然后，进一步考虑控制输入饱和、死区等非线性特性，对控制律进行改进.通过在相同仿真参数条件下对本文所提出的两种控制律进行仿真，验证了两种控制律的有效性，并且改进后的控制律在燃料消耗略微增加的情况下明显地提高了控制精度.

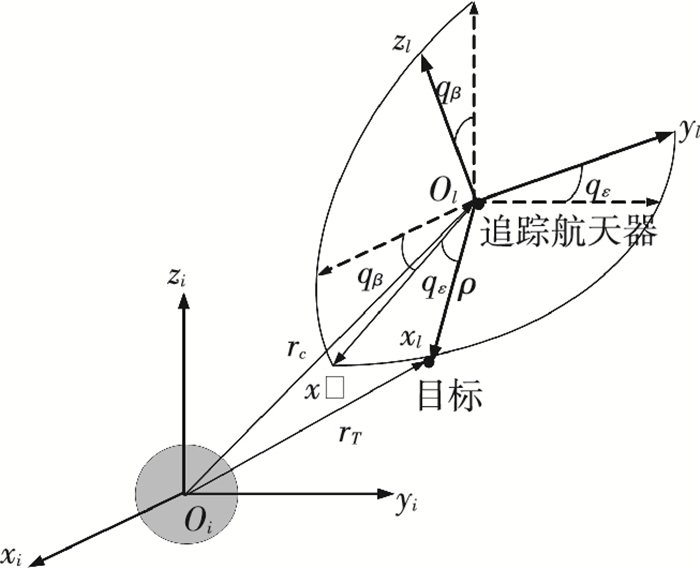
1 相对运动模型 1.1 视线坐标系

图 1中下标i表示惯性坐标系，l表示视线坐标系.惯性系O_ix_iy_iz_i与视线系O_lx_ly_lz_l及其关系如图 1所示，O_l为视线系的原点，位于追踪航天器质心，x_l轴与视线重合，y_l轴位于由x_l轴和y_i轴组成的平面内且与x_l轴垂直，z_l轴由右手定则确定.q_ε和q_β分别称为视线倾角和视线偏角，ρ为目标相对于追踪航天器的位置矢量^[5].

1.2 相对轨道动力学模型

相对轨道的动力学方程在视线系的投影为^[5]

$ \begin{array}{l} {\left( {\frac{{{d^2}\mathit{\boldsymbol{\rho }}}}{{{\rm{d}}{t^2}}}} \right)_l} = \frac{{{d^2}{{\left( \mathit{\boldsymbol{\rho }} \right)}_l}}}{{{\rm{d}}{t^2}}} + \left( {{{\mathit{\boldsymbol{\dot \omega }}}_l}} \right)_l^ \times {\left( \mathit{\boldsymbol{\rho }} \right)_l} + 2\left( {{\mathit{\boldsymbol{\omega }}_l}} \right)_l^ \times \frac{{{\rm{d}}{{\left( \mathit{\boldsymbol{\rho }} \right)}_l}}}{{{\rm{d}}t}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{\mathit{\boldsymbol{\omega }}_l}} \right)_l^ \times \left( {{\mathit{\boldsymbol{\omega }}_l}} \right)_l^ \times {\left( \mathit{\boldsymbol{\rho }} \right)_l} = {\left( {\Delta \mathit{\boldsymbol{g}}} \right)_l} + {\left( \mathit{\boldsymbol{f}} \right)_l} - {\left( {{\mathit{\boldsymbol{u}}_c}} \right)_l}. \end{array} $

(1)

式中：×为反对称矩阵；Δg =[Δg_x, Δg_y, Δg_z]^T为目标和追踪航天器间的引力差 (在对目标进行近距离接近和跟踪时，该项可以忽略)；f =[f_x, f_y, f_z]^T为目标的加速度，且对于追踪航天器是未知的；u_c=[u_cx, u_cy, u_cz]^T为追踪航天器的控制加速度，其中下标c为追踪航天器.将式 (1) 写成分量的形式：

$ \left\{ \begin{array}{l} \ddot \rho - \rho \left( {\dot q_\varepsilon ^2 + \dot q_\beta ^2{{\cos }^2}{q_\varepsilon }} \right) = \Delta {\mathit{g}_x} + {f_x} - {u_{cx}},\\ \rho {{\ddot q}_\varepsilon } + 2\dot \rho {{\dot q}_\varepsilon } + \rho \dot q_\beta ^2\sin {q_\varepsilon }\cos {q_\varepsilon } = \Delta {\mathit{g}_y} + {f_y} - {u_{cy}},\\ - \rho {{\ddot q}_\beta }\cos {q_\varepsilon } + 2\rho {{\dot q}_\beta }{{\dot q}_\varepsilon }\sin {q_\varepsilon } - 2\dot \rho {{\dot q}_\beta }\cos {q_\varepsilon } = \\ \Delta {\mathit{g}_z} + {f_z} - {u_{cz}}. \end{array} \right. $

(2)

1.3 姿态动力学模型与运动学模型

追踪航天器的姿态动力学方程为

$ {\mathit{\boldsymbol{J}}_c}{{\mathit{\boldsymbol{\dot \omega }}}_{bc}} + \mathit{\boldsymbol{\omega }}_{bc}^ \times {\mathit{\boldsymbol{J}}_c}{\mathit{\boldsymbol{\omega }}_{bc}} = {\mathit{\boldsymbol{T}}_c}. $

(3)

式中：J_c=diag (J_c1, J_c2, J_c3) 为转动惯量矩阵；下标b为航天器体坐标系；ω_bc=[ω_x, ω_y, ω_z]^T为相对惯性系的姿态角速度；T_c为控制力矩.

定义追踪航天器按zxy转序绕本体x、y、z轴的转角分别为φ、θ、ψ，则追踪航天器角速度可以表示为

$ \left[ {\begin{array}{*{20}{c}} {{\omega _x}}\\ {{\omega _y}}\\ {{\omega _z}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \theta } & 0 & { - \sin \theta \cos \varphi }\\ 0 & 1 & {\sin \varphi }\\ {\sin \theta } & 0 & {\cos \theta \cos \varphi } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\dot \varphi }\\ {\dot \theta }\\ {\dot \psi } \end{array}} \right]. $

(4)

为了表达式的简便，定义矩阵R为

$ \begin{array}{l} \mathit{\boldsymbol{R = }}{\left[ {\begin{array}{*{20}{c}} {\cos \theta } & 0 & { - \sin \theta \cos \varphi }\\ 0 & 1 & {\sin \varphi }\\ {\sin \theta } & 0 & {\cos \theta \cos \varphi } \end{array}} \right]^{ - 1}} = \\ \;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {\cos \theta } & 0 & {\sin \theta }\\ {\sin \theta \sin \varphi /\cos \varphi } & 1 & { - \cos \theta \sin \varphi /\cos \varphi }\\ { - \sin \theta /\cos \varphi } & 0 & {\cos \theta /\cos \varphi } \end{array}} \right], \end{array} $

(5)

则有

$ \left[ {\begin{array}{*{20}{c}} {\dot \varphi }\\ {\dot \theta }\\ {\dot \psi } \end{array}} \right] = \mathit{\boldsymbol{R}}\left[ {\begin{array}{*{20}{c}} {{\omega _x}}\\ {{\omega _y}}\\ {{\omega _z}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\omega _x}\cos \theta + {\omega _z}\sin \theta }\\ {\left( {{\omega _x}\sin \theta - {\omega _z}\cos \theta } \right)\tan \varphi + {\omega _y}}\\ {\left( {{\omega _z}\cos \theta - {\omega _x}\sin \theta } \right)\sec \varphi } \end{array}} \right]. $

(6)

1.4 期望轨道解算

当非合作目标存在姿态翻滚时，在视线系下特征点的相对位置会改变，从而导致追踪航天器的期望轨道变化.设目标的特征点在其体坐标系下的单位矢量为n_b，则追踪航天器视线的期望方向为-n_b.所以追踪航天器期望视线方向在惯性系下的投影为^[5]

$ {\mathit{\boldsymbol{\rho }}_i} = \mathit{\boldsymbol{C}}_i^{bt}\left( { - {\mathit{\boldsymbol{n}}_b}{\rho _f}} \right) = {\left[ {\begin{array}{*{20}{c}} {{x_i}} & {{y_i}} & {{z_i}} \end{array}} \right]^{\rm{T}}}. $

(7)

式中：C_i^bt为目标体坐标系到惯性系的余弦矩阵.视线方向在视线坐标系下的期望值为ρ_l=[ρ_f, 0, 0]^T，其中ρ_f为追踪航天器与目标之间的期望距离，投影到惯性坐标系可得

$ {\mathit{\boldsymbol{\rho }}_i} = \mathit{\boldsymbol{C}}_i^l{\mathit{\boldsymbol{\rho }}_l}, $

(8)

式中，C_i^l为视线系到惯性系的余弦矩阵.根据式 (7)~(8) 可计算得到视线倾角和视线偏角的期望值q_εf和q_βf，对式 (7)~(8) 分别进行求导并联立即可求出视线倾角和视线偏角导数的期望值${{\dot q}_{\varepsilon f}}$和${{\dot q}_{\beta f}}$.

1.5 期望姿态解算

在近距离跟踪非合作目标过程中，追踪航天器将实时对目标观测.假设观测装置中心线沿追踪航天器体坐标系的期望x_bcf轴方向，要求x_bc轴保持沿视线轴方向，则追踪航天器体坐标系三轴期望的单位矢量为^[5]

$ {\mathit{\boldsymbol{x}}_{bef}} = \frac{{{\mathit{\boldsymbol{\rho }}_i}}}{{{\rho _f}}},{\mathit{\boldsymbol{y}}_{bcf}} = \frac{{\mathit{\boldsymbol{\rho }}_i^ \times \mathit{\boldsymbol{\hat s}}}}{{{{\left\| {\mathit{\boldsymbol{\rho }}_i^ \times \mathit{\boldsymbol{\hat s}}} \right\|}_2}}},{z_{bef}} = \mathit{\boldsymbol{x}}_{bcf}^ \times {\mathit{\boldsymbol{y}}_{bcf}}. $

(9)

式中，ŝ为太阳矢量，在执行在轨任务的过程中为了能为星体提供电能，要求帆板垂直于入射光线，设帆板沿追踪航天器y_bc轴安装.再由关系式：

$ {I_3} = \mathit{\boldsymbol{C}}_{bc}^i\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}_{bcf}}} & {{\mathit{\boldsymbol{y}}_{bcf}}} & {{\mathit{\boldsymbol{z}}_{bcf}}} \end{array}} \right], $

即可求解期望姿态角φ_f、θ_f、ψ_f，对式 (9) 求导并利用式 (4) 即可求解期望姿态角速度.

1.6 控制模型状态空间表达式

针对本文所研究的问题，由于非合作目标的轨道机动未知，因此对于追踪航天器，在任务初始时刻是偏离期望轨道的，从而需要调整相对轨道以达到对目标跟踪监视的要求.然后进行跟踪保持控制，而目标的姿态信息是能够获取的，所以追踪航天器在初始时刻的姿态是接近期望姿态的，则式 (10) 是近似成立的.

$ \left[ {\begin{array}{*{20}{c}} {{{\dot \varphi }_f}}\\ {{{\dot \theta }_f}}\\ {{{\dot \psi }_f}} \end{array}} \right] = \mathit{\boldsymbol{R}}\left[ {\begin{array}{*{20}{c}} {{\omega _{xf}}}\\ {{\omega _{yf}}}\\ {{\omega _{zf}}} \end{array}} \right]. $

(10)

设x₁=[ρ, q_ε, q_β, φ, θ, ψ]^T，${x_2} = {[\dot \rho ,{{\dot q}_\varepsilon },{{\dot q}_\beta },{\omega _x},{\omega _y},{\rm{ }}{\omega _z}]^{\rm{T}}}$，选取误差量为状态变量，记e₁=[ρ_f-ρ, q_εf-q_ε, q_βf-q_β, φ_f-φ, θ_f-θ, ψ_f-ψ]^T，${e_2} = {[{{\dot \rho }_f} - \dot \rho ,{{\dot q}_{\varepsilon f}} - {{\dot q}_\varepsilon },{\rm{ }}{{\dot q}_{\beta f}} - {{\dot q}_\beta },{\omega _{xf}} - {\omega _x},{\omega _{yf}} - {\omega _y},{\omega _{zf}} - {\omega _z}]^{\rm{T}}}$，由式 (2)、式 (3)、式 (5)、式 (6) 和式 (10) 可得到如下状态空间表达式：

$ \left\{ \begin{array}{l} {{\dot e}_1} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_{3 \times 3}}} & {{0_{3 \times 3}}}\\ {{0_{3 \times 3}}} & \mathit{\boldsymbol{R}} \end{array}} \right]{e_2},\\ {{\dot e}_2} = - \left[ {\begin{array}{*{20}{c}} {\rho \dot q_\varepsilon ^2 + \rho \dot q_\beta ^2{{\cos }^2}{q_\varepsilon }}\\ { - 2\dot \rho {{\dot q}_\varepsilon }/\rho - \dot q_\beta ^2\sin {q_\varepsilon }\cos {q_\varepsilon }}\\ {2{{\dot q}_\beta }{{\dot q}_\varepsilon }\sin {q_\varepsilon }/\cos {q_\varepsilon } - 2\dot \rho {{\dot q}_\beta }/\rho }\\ {\left( {{J_{cy}} - {J_{cz}}} \right){\omega _y}{\omega _z}/{J_{cx}}}\\ {\left( {{J_{cz}} - {J_{cx}}} \right){\omega _x}{\omega _z}/{J_{cy}}}\\ {\left( {{J_{cx}} - {J_{cy}}} \right){\omega _y}{\omega _x}/{J_{cz}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{{\ddot \rho }_f} - {f_x}}\\ {{{\ddot q}_{\varepsilon f}} - {f_y}/\rho }\\ {{{\ddot q}_{\beta f}} + {f_z}/\left( {\rho \cos {q_\varepsilon }} \right)}\\ {{{\dot \omega }_{xf}}}\\ {{{\dot \omega }_{yf}}}\\ {{{\dot \omega }_{zf}}} \end{array}} \right] + \\ \;\;\;\;\;\;\;\; \left[ {\begin{array}{*{20}{c}} {{u_{cx}}}\\ {{u_{cy}}/\rho }\\ { - {u_{cz}}/\left( {\rho \cos {q_\varepsilon }} \right)}\\ { - {T_{cx}}/{J_{cx}}}\\ { - {T_{cy}}/{J_{cy}}}\\ { - {T_{cz}}/{J_{cz}}} \end{array}} \right] \end{array} \right.. $

(11)

本文将结合式 (11) 所示的非合作目标相对运动模型进行控制律设计，实现对空间非合作目标的接近、跟踪以及指向等控制需求.

2 非合作目标自适应神经网络有限时间控制律设计 2.1 自适应神经网络有限时间控制律设计

引理1    ^[16]对于非线性系统：

$ \dot x = f\left( x \right),f\left( 0 \right) = 0,x \in {{\bf{R}}^n}. $

(12)

假设存在定义在Rⁿ原点邻域Û内的连续函数V(x)，且实数c > 0, 0 < α < 1，满足：

1) V(x) 在Û中正定；

2) $\dot V(x) + c{V^\alpha }(x) \le 0,\forall x \in \hat U$.

则系统 (12) 在Û内有限时间稳定.若Û = Rⁿ且V(x) 径向无界 (V(x)→+∞时，‖x‖→+∞)，则系统 (12) 的原点全局有限时间稳定.

对于近距离跟踪指向空间非合作机动目标的问题，由式 (11) 所组成的非合作目标相对运动模型可以写成如下不确定非线性动态系统形式:

$ \left\{ \begin{array}{l} {{\dot e}_1} = A\left( {{x_1}} \right){e_2},\\ {{\dot e}_2} = f\left( \mathit{\boldsymbol{x}} \right) + w + g\left( \mathit{\boldsymbol{x}} \right)u. \end{array} \right. $

(13)

式中：e₁, e₂, x₁, x₂∈ R⁶，x =[x₁^T, x₂^T]^T.A(x₁)∈ R^6×6，f(x)∈ R⁶，g(x)∈ R^6×6根据式 (10)~(11) 获得，且可以发现都是关于x的已知光滑非线性函数，且A(x₁) 与g(x) 非奇异.u∈ R⁶为控制输入.由于非合作目标的轨道机动情况未知，因此其加速度以及期望相对位置状态的二阶导数等未知，因此w未知，即为模型不确定性.假设‖w‖≤d，其中d > 0.

用一个三层神经网络自适应估计式 (13) 中的不确定项w，并进行补偿.w的估计值${\hat w}$可表示为

$ \hat w = {{\mathit{\boldsymbol{\hat \theta }}}^{\rm{T}}}\varphi \left( e \right). $

式中：系统 (13) 的状态量x是神经网络的输入向量；${\mathit{\boldsymbol{\hat \theta }}}$为加权矩阵θ的估计值.设n > 1是神经元的数量，即φ(e)=[φ₁(e), φ₂(e), …, φ_n(e)]^T，其中φ_i(·) 是高斯RBF函数为

$ {\varphi _i}\left( e \right) = \exp \left[ { - \frac{{{{\left\| {e - {c_i}} \right\|}^2}}}{{2\sigma _i^2}}} \right],i = 1,2, \cdots ,n. $

(14)

式中：c_i∈ Rⁿ, σ_i > 0分别为第i个基函数的中心和宽度.

根据RBF神经网络逼近非线性函数的原理，根据文献[12]，一般存在如下假设条件.

假设1    对于任意给定的足够小的正数ε_N，总能找到最优加权矩阵θ^*使逼近误差满足.

假设2    最优加权矩阵θ^*是有界的，即存在一个正常数λ，满足‖ θ^*‖_∞≤λ.

因此非线性不确定函数w可以表示成

$ w = {\mathit{\boldsymbol{\theta }}^{ * {\rm{T}}}}\varphi \left( e \right) + \varepsilon . $

为了后续设计非合作目标控制律的需要，定义向量sig (·)^α∈ Rⁿ的形式如下：

$ {\rm{sig}}{\left( \xi \right)^\alpha } = {\left[ {{{\left| {{\xi _1}} \right|}^\alpha }{\mathop{\rm sgn}} \left( {{\xi _1}} \right), \cdots ,{{\left| {{\xi _n}} \right|}^\alpha }{\mathop{\rm sgn}} \left( {{\xi _n}} \right)} \right]^{\rm{T}}}, $

给出辅助控制器ν(e₁)=-A^-1(x₁)K₁sig (e₁)^α，其中K₁=diag (k₁₁, …, k_1n) > 0，0 < α < 1.定义误差变量为

$ z = {e_2} - \nu \left( {{e_1}} \right), $

(15)

将式 (15) 代入系统 (13) 得到：

$ \left\{ \begin{array}{l} {{\dot e}_1} = A\left( {{x_1}} \right)\left( {z + \nu \left( {{e_1}} \right)} \right),\\ \dot z = f\left( \mathit{\boldsymbol{x}} \right) + w + g\left( \mathit{\boldsymbol{x}} \right)u - \dot \nu \left( {{e_1}} \right). \end{array} \right. $

(16)

对于系统 (13)，给出如下自适应控制律：

$ \begin{array}{l} u = {g^{ - 1}}\left( x \right)\left( {\dot \nu \left( {{e_1}} \right) - f\left( x \right) - {A^{\rm{T}}}\left( {{x_1}} \right){e_1} - } \right.\\ \;\;\;\;\;\;\left. {{K_2}{\rm{sig}}{{\left( z \right)}^\alpha } - {{\mathit{\boldsymbol{\hat \theta }}}^{\rm{T}}}\varphi \left( e \right) - {K_3}{\mathop{\rm sgn}} \left( z \right)} \right), \end{array} $

(17)

$ \dot{\hat{\theta }}=\mathit{\boldsymbol{ }}\!\!\Gamma\!\!\rm{ }\varphi \left( e \right){{z}^{\rm{T}}}. $

(18)

式中：K₂=diag (k₂₁, …, k_2n) > 0，K₃ > 0，Γ为一个正定对角矩阵.

注1    由于sig (e₁)^α在e_1i=0且${{\dot e}_{1i}} \ne 0$时的微分出现奇异现象，设置一个阈值λ来判断奇异.因此定义$\dot \nu \left( {{e_1}} \right)$如下：

$ \begin{array}{*{20}{c}} {\dot \nu \left( {{e_1}} \right) = \left\{ \begin{array}{l} - {{\dot A}^{ - 1}}\left( {{x_1}} \right){K_1}{\rm{sig}}{\left( {{e_1}} \right)^\alpha } - {A^{ - 1}}\left( {{x_1}} \right)\eta \left( {{e_1}} \right),{{\dot e}_1} \ne 0;\\ 0,{{\dot e}_1} = 0. \end{array} \right.}\\ {{\eta _i}\left( {{e_{1i}}} \right) = \left\{ \begin{array}{l} {k_{1i}}\alpha {\left| {{e_{1i}}} \right|^{\alpha - 1}}{{\dot e}_{1i}},\left| {{e_{1i}}} \right| \ge \lambda ;\\ {k_{1i}}\alpha {\left| {{\Delta _i}} \right|^{\alpha - 1}}{{\dot e}_{1i}},\left| {{e_{1i}}} \right| < \lambda . \end{array} \right.} \end{array} $

式中：λ、Δ_i分别为小的正常数；e_1i为向量e₁的第i个元素；η_i(e_1i) 为向量η(e₁) 的第i个元素.

定理1    对于非合作目标控制系统 (13)，假设1和2均成立，则在控制律 (17)~(18) 作用下，闭环系统是全局有限时间稳定的.

证    将控制律 (17) 代入式 (16) 可得

$ \left\{ \begin{array}{l} {{\dot e}_1} = - {K_1}{\rm{sig}}{\left( {{e_1}} \right)^\alpha } + A\left( {{x_1}} \right)z,\\ \dot z = - {A^{\rm{T}}}\left( {{x_1}} \right){x_1} - {K_2}{\rm{sig}}{\left( z \right)^\alpha } + \\ \;\;\;\;\;\;w - {{\mathit{\boldsymbol{\hat \theta }}}^{\rm{T}}}\varphi \left( e \right) - {K_3}{\mathop{\rm sgn}} \left( z \right). \end{array} \right. $

(19)

首先, 证明闭环系统 (19) 是全局渐近稳定的.

设$\tilde \theta = {\theta ^*} - \hat \theta $，则$\mathop {\tilde \theta }\limits^. = {{\dot \theta }^*} - \mathop {\hat \theta }\limits^. = - \mathop {\hat \theta }\limits^. $，选取Lyapunov函数

$ {V_1} = \frac{1}{2}e_1^{\rm{T}}{e_1} + \frac{1}{2}{z^{\rm{T}}}z + \frac{1}{2}{\rm{tr}}\left( {{{\mathit{\boldsymbol{\tilde \theta }}}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{ - 1}}\mathit{\boldsymbol{\tilde \theta }}} \right), $

(20)

选取K₃ > ε_N > ‖ε‖_∞，对式 (20) 求导，并由式 (19) 可得

$ \begin{array}{l} {{\dot V}_1} = e_1^{\rm{T}}{{\dot e}_1} + {z^{\rm{T}}}\dot z + {\rm{tr}}\left( {{{\mathit{\boldsymbol{\tilde \theta }}}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{ - 1}}\mathit{{\mathit{\dot{\tilde{\theta }}}}}} \right) = \\ \;\;\;\;\;\; - e_1^{\rm{T}}{K_1}{\rm{sig}}{\left( {{e_1}} \right)^\alpha } - {z^{\rm{T}}}{K_2}{\rm{sig}}{\left( z \right)^\alpha } + {\rm{tr}}\left( {{{\mathit{\boldsymbol{\tilde \theta }}}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{ - 1}}{\mathit{\dot{\tilde{\theta }}}}} \right) + \\ \;\;\;\;\;\;\;{z^{\rm{T}}}\left( {{\mathit{\boldsymbol{\theta }}^{ * {\rm{T}}}}\varphi \left( e \right) + \varepsilon - {{\mathit{\boldsymbol{\hat \theta }}}^{\rm{T}}}\varphi \left( e \right) - {K_3}{\rm{sgn}}\left( z \right)} \right) = \\ \;\;\;\;\;\;\; - e_1^{\rm{T}}{K_1}{\rm{sig}}{\left( {{e_1}} \right)^\alpha } - {z^{\rm{T}}}{K_2}{\rm{sig}}{\left( z \right)^\alpha } + {z^{\rm{T}}}\varepsilon - \\ \;\;\;\;\;\;\;{K_3}{\left\| z \right\|_1} + {\rm{tr}}\left( {{{\mathit{\boldsymbol{\tilde \theta }}}^{\rm{T}}}\varphi \left( e \right){\mathit{\boldsymbol{z}}^{\rm{T}}}\mathit{\boldsymbol{ + }}{{\mathit{\boldsymbol{\tilde \theta }}}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{ - 1}}{\mathit{\boldsymbol{\dot{\tilde{\theta}}}}}} \right) = \\ \;\;\;\;\;\;\;\; - e_1^{\rm{T}}{K_1}{\rm{sig}}{\left( {{e_1}} \right)^\alpha } - {z^{\rm{T}}}{K_2}{\rm{sig}}{\left( z \right)^\alpha } + {\left\| z \right\|_1}\left( {{\varepsilon _N} - } \right.\\ \;\;\;\;\;\;\;\;\left. {{K_3}} \right) \le - e_1^{\rm{T}}{K_1}{\rm{sig}}{\left( {{e_1}} \right)^\alpha } - {z^{\rm{T}}}{K_2}{\rm{sig}}{\left( z \right)^\alpha } \le 0. \end{array} $

(21)

从式 (21) 可得e₁、z和${\tilde \theta }$有界，由ν(e₁) 和z的定义可知e₂有界，对于系统 (12)，由于一般${{\dot e}_2}$也是有界的，因此由Barbalat引理可知，当t→∞时，e₁→0，z→0，e₂→0，因此闭环系统 (13) 是全局渐近稳定的.

然后, 证明闭环系统 (19) 是全局有限时间稳定的.

由式 (14) 可知高斯函数0 < φ_i(e)≤1，则‖φ(e)‖_∞有界，根据范数的基本放缩性质，可以得到:

$ {\left\| {{{\mathit{\boldsymbol{\tilde \theta }}}^{\rm{T}}}\varphi \left( e \right)} \right\|_\infty } \le {\left\| {\mathit{\boldsymbol{\tilde \theta }}} \right\|_\infty }\;\;{\left\| {\varphi \left( e \right)} \right\|_\infty }, $

又由于${\tilde \theta }$的有界性，可以得到${\left\| {{{\mathit{\boldsymbol{\tilde \theta }}}^{\rm{T}}}\varphi \left( e \right)} \right\|_\infty }$也是有界的.选取Lyapunov函数

$ V = \frac{1}{2}e_1^{\rm{T}}{e_1} + \frac{1}{2}{z^{\rm{T}}}z. $

(22)

式中：选取K₃ > ε_N+${\left\| {{{\mathit{\boldsymbol{\tilde \theta }}}^{\rm{T}}}\varphi \left( e \right)} \right\|_\infty }$，对式 (22) 求导，并将式 (19) 带入可得

$ \begin{array}{l} \dot V = - e_1^{\rm{T}}{K_1}{\rm{sig}}{\left( {{e_1}} \right)^\alpha } - {z^{\rm{T}}}{K_2}{\rm{sig}}{\left( z \right)^\alpha } + \\ \;\;\;\;\;\;\;{z^{\rm{T}}}\left( {w - {{\mathit{\boldsymbol{\hat \theta }}}^{\rm{T}}}\varphi \left( e \right) - {K_3}{\mathop{\rm sgn}} \left( z \right)} \right) \le \\ \;\;\;\;\;\;\; - e_1^{\rm{T}}{K_1}{\rm{sig}}{\left( {{e_1}} \right)^\alpha } - {z^{\rm{T}}}{K_2}{\rm{sig}}{\left( z \right)^\alpha } + \\ \;\;\;\;\;\;\;{\left\| z \right\|_1}\left( {{\varepsilon _N} + {{\left\| {{{\mathit{\boldsymbol{\tilde \theta }}}^{\rm{T}}}\varphi \left( e \right)} \right\|}_\infty } - {K_3}} \right) \le \\ \;\;\;\;\;\;\; - e_1^{\rm{T}}{K_1}{\rm{sig}}{\left( {{e_1}} \right)^\alpha } - {z^{\rm{T}}}{K_2}{\rm{sig}}{\left( z \right)^\alpha } = \\ \;\;\;\;\;\;\; - \sum\limits_{i = 1}^n {{k_{1i}}{{\left| {{e_{1i}}} \right|}^{1 + \alpha }}} - \sum\limits_{i = 1}^n {{k_{2i}}{{\left| {{z_i}} \right|}^{1 + \alpha }}} \le \\ \;\;\;\;\;\;\;\; - {{\bar k}_1}{\left( {\frac{1}{2}\sum\limits_{i = 1}^n {e_{1i}^2} } \right)^\mu } - {{\bar k}_2}{\left( {\frac{1}{2}\sum\limits_{i = 1}^n {z_{1i}^2} } \right)^\mu } \le \bar k{V^\mu }. \end{array} $

(23)

式中：μ=(1+α)/2，0.5 < μ < 1；k_1min=min{k_1i}，k_2min=min{k_2i}；k₁=2^μk_1min，k₂=2^μk_2min，k=min{k₁, k₂}.

因此，根据引理1，对于给定的初始状态e(0)=e₀，e₁和z将在有限时间内收敛到0.由ν(e₁) 和z的定义可知，当e₁=0, z=0时，e₂=0，因此闭环系统 (19) 是全局有限时间稳定的.

2.2 考虑输入非线性有限时间控制律设计

对于近距离跟踪指向非合作机动目标的问题，进一步考虑实际系统普遍存在的控制输入饱和、死区等非线性特性.因此将系统 (13) 改写成如下形式：

$ \left\{ \begin{array}{l} {{\dot e}_1} = A\left( {{x_1}} \right){e_2},\\ {{\dot e}_2} = f\left( \mathit{\boldsymbol{x}} \right) + w + g\left( \mathit{\boldsymbol{x}} \right)D\left( u \right). \end{array} \right. $

(24)

式中，D(u) 为控制器的实际输出，与理想控制输出u、控制偏差Δu之间满足如下关系式：

$ D\left( u \right) = u - \Delta u. $

为了达到更好的控制效果，采用RBF神经网络逼近g(x)Δu，可以得到：

$ g\left( \mathit{x} \right)\Delta u = \mathit{\boldsymbol{\theta }}_\Delta ^{ * {\rm{T}}}{\varphi _\Delta }\left( \mathit{\boldsymbol{y}} \right) + {\varepsilon _\Delta }. $

式中：φ_Δ(y) 为高斯函数向量；输入向量y =[e^T, u^T]^T，逼近误差ε_Δ和最优加权矩阵θ_Δ^*也分别满足假设1和2，即ε_Δ存在逼近误差上界ε_ΔN，${\left\| {\mathit{\boldsymbol{\tilde \theta }}_\Delta ^{\rm{T}}{\varphi _\Delta }\left( \mathit{\boldsymbol{y}} \right)} \right\|_\infty }$有界.

对于不确定非线性动态系统 (24)，给出如下自适应控制律：

$ \begin{array}{l} u = {g^{ - 1}}\left( x \right)\left[ {\dot \nu \left( {{e_1}} \right) - f\left( x \right) - {A^{\rm{T}}}\left( {{x_1}} \right){e_1} - {K_2}{\rm{sig}}{{\left( z \right)}^\alpha }} \right] + \\ \;\;\;\;\;\;{g^{ - 1}}\left( x \right)\left[ { - {{\mathit{\boldsymbol{\hat \theta }}}^{\rm{T}}}\varphi \left( e \right) - {K_3}{\mathop{\rm sgn}} \left( z \right) + \mathit{\boldsymbol{\hat \theta }}_\Delta ^{\rm{T}}{\varphi _\Delta }\left( \mathit{\boldsymbol{y}} \right)} \right], \end{array} $

(25)

$ \left\{ \begin{array}{l} {\dot{\hat{\theta }}} = \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\varphi \left( e \right){z^{\rm{T}}},\\ {{\dot{\hat{\theta }}}_\Delta } = - {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\Delta }{\varphi _\Delta }\left( \mathit{\boldsymbol{y}} \right){z^{\rm{T}}}. \end{array} \right. $

(26)

式中，Γ_Δ为正定对角矩阵.

定理2    对于非合作目标控制系统 (24)，假设1和2均成立，则在控制律 (25)~(26) 作用下，闭环系统是全局有限时间稳定的.

证    将控制律 (25) 代入系统 (24) 可得

$ \left\{ \begin{array}{l} {{\dot e}_1} = - {K_1}{\rm{sig}}{\left( {{e_1}} \right)^\alpha } + A\left( {{x_1}} \right)z\\ \dot z = - {A^{\rm{T}}}\left( {{x_1}} \right){e_1} - {K_2}{\rm{sig}}{\left( z \right)^\alpha } + w - {{\mathit{\boldsymbol{\hat \theta }}}^{\rm{T}}}\varphi \left( e \right) - \\ \;\;\;\;\;{K_3}{\mathop{\rm sgn}} \left( z \right) - g\left( x \right)\Delta u + \mathit{\boldsymbol{\hat \theta }}_\Delta ^{\rm{T}}{\varphi _\Delta }\left( \mathit{\boldsymbol{y}} \right). \end{array} \right. $

(27)

首先, 证明闭环系统 (27) 是全局渐近稳定的.

设${{\tilde \theta }_\Delta } = \theta _\Delta ^* - {{\hat \theta }_\Delta }\;$，则$\mathop {{{\tilde \theta }_\Delta }}\limits^. = \dot \theta _\Delta ^* - {\mathop {\hat \theta }\limits^. _\Delta } = - {\mathop {\hat \theta }\limits^. _\Delta }$，选取Lyapunov函数

$ {V_2} = \frac{1}{2}e_1^{\rm{T}}{e_1} + \frac{1}{2}{z^{\rm{T}}}z + \frac{1}{2}{\rm{tr}}\left( {{{\mathit{\boldsymbol{\tilde \theta }}}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{ - 1}}\mathit{\tilde \theta }} \right) + \frac{1}{2}{\rm{tr}}\left( {\mathit{\boldsymbol{\tilde \theta }}_\Delta ^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\Delta ^{ - {\rm{1}}}{{\mathit{\tilde \theta }}_\Delta }} \right), $

(28)

选取K₃ > ε_N+ε_ΔN>‖ε‖_∞+‖ε_Δ‖_∞，对式 (28) 求导，并由系统 (27) 及式 (25) 可得

$ \begin{array}{l} {{\dot V}_2} = - e_1^{\rm{T}}{K_1}{\rm{sig}}{\left( {{e_1}} \right)^\alpha } - {z^{\rm{T}}}{K_2}{\rm{sig}}{\left( z \right)^\alpha } + {\rm{tr}}\left( {\mathit{\boldsymbol{\tilde \theta }}_\Delta ^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\Delta ^{ - {\rm{1}}}{{\mathrm{\dot{\tilde{\theta}}}}_\Delta }} \right) + \\ \;\;\;\;\;\;\;{z^{\rm{T}}}\left( {\varepsilon - {K_3}{\mathop{\rm sgn}} \left( z \right) + \mathit{\boldsymbol{\hat \theta }}_\Delta ^{\rm{T}}{\varphi _\Delta }\left( \mathit{\boldsymbol{y}} \right) - g\left( x \right)\Delta u} \right) = \\ \;\;\;\;\;\;\; - e_1^{\rm{T}}{K_1}{\rm{sig}}{\left( {{e_1}} \right)^\alpha } - {z^{\rm{T}}}{K_2}{\rm{sig}}{\left( z \right)^\alpha } + {\rm{tr}}\left( {\mathit{\boldsymbol{\tilde \theta }}_\Delta ^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_\Delta ^{ - {\rm{1}}}{{\mathrm{\dot{\tilde{\theta}}}}_\Delta }} \right) + \\ \;\;\;\;\;\;\;\;{z^{\rm{T}}}\left( {\varepsilon - {\varepsilon _\Delta } - {K_3}{\mathop{\rm sgn}} \left( z \right)} \right) + {\rm{tr}}\left( { - \mathit{\boldsymbol{\tilde \theta }}_\Delta ^{\rm{T}}{\varphi _\Delta }\left( \mathit{\boldsymbol{y}} \right){z^{\rm{T}}}} \right) \le \\ \;\;\;\;\;\;\;\; - e_1^{\rm{T}}{K_1}{\rm{sig}}{\left( {{e_1}} \right)^\alpha } - {z^{\rm{T}}}{K_2}{\rm{sig}}{\left( z \right)^\alpha } + \\ \;\;\;\;\;\;\;\;\;{\left\| z \right\|_1}\left( {{\varepsilon _N} + {\varepsilon _{\Delta N}} - {K_3}} \right) \le 0. \end{array} $

所以闭环系统 (24) 是全局渐近稳定的.

然后, 证明闭环系统 (27) 全局有限时间稳定.

同样选取式 (22) 的Lyapunov函数形式，令${K_3} > {\varepsilon _N} + {\left\| {{{\mathit{\boldsymbol{\tilde \theta }}}^{\rm{T}}}\varphi \left( e \right)} \right\|_\infty } + {\varepsilon _{\Delta N}} + {\left\| {\mathit{\boldsymbol{\tilde \theta }}_\Delta ^{\rm{T}}{\varphi _\Delta }\left( \mathit{\boldsymbol{y}} \right)} \right\|_\infty }$，对式 (22) 求导，并由系统 (27) 及式 (23) 可得

$ \begin{array}{l} \dot V = e_1^{\rm{T}}{{\dot e}_1} + {z^{\rm{T}}}z = \\ \;\;\;\;\;\; - e_1^{\rm{T}}{K_1}{\rm{sig}}{\left( {{e_1}} \right)^\alpha } - {z^{\rm{T}}}{K_2}{\rm{sig}}{\left( z \right)^\alpha } + \\ \;\;\;\;\;\;{z^{\rm{T}}}\left( {\varepsilon - {K_3}{\mathop{\rm sgn}} \left( z \right) - g\left( x \right)\Delta u + {{\mathit{\boldsymbol{\hat \theta }}}^{\rm{T}}}\varphi \left( e \right) + } \right.\\ \;\;\;\;\;\;\left. {\mathit{\boldsymbol{\tilde \theta }}_\Delta ^{\rm{T}}{\varphi _\Delta }\left( \mathit{\boldsymbol{y}} \right)} \right) \le - e_1^{\rm{T}}{K_1}{\rm{sig}}{\left( {{e_1}} \right)^\alpha } - {z^{\rm{T}}}{K_2}{\rm{sig}}{\left( z \right)^\alpha } + \\ \;\;\;\;\;\;{\left\| z \right\|_1}\left( {{\varepsilon _N} + {\varepsilon _{\Delta N}} - {{\left\| {{{\mathit{\boldsymbol{\hat \theta }}}^{\rm{T}}}\varphi \left( e \right)} \right\|}_\infty } + } \right.\\ \;\;\;\;\;\;\left. {{{\left\| {\mathit{\boldsymbol{\tilde \theta }}_\Delta ^{\rm{T}}{\varphi _\Delta }\left( \mathit{\boldsymbol{y}} \right)} \right\|}_\infty } - {K_3}} \right) \le - e_1^{\rm{T}}{K_1}{\rm{sig}}{\left( {{e_1}} \right)^\alpha } - \\ \;\;\;\;\;\;{z^{\rm{T}}}{K_2}{\rm{sig}}{\left( z \right)^\alpha } \le - \bar k{V^\mu }. \end{array} $

因此，类似式 (23) 的处理过程，同理可以得到x₁、z和x₂在有限时间内收敛到0，因此闭环系统 (27) 是全局有限时间稳定的.

3 仿真校验

分别应用定理1，2的有限时间控制算法来解决近距离跟踪指向非合作机动目标的问题，其中目标的加速度矢量在本文提出的两种控制算法中未直接使用，而是采用RBF神经网络来估计.对于由式 (12) 构成的系统，分别按照式 (17) 和式 (25) 设计控制器，按照式 (18) 和式 (26) 设计神经网络加权矩阵更新律进行仿真，并加入控制饱和、死区等特性.

3.1 仿真参数

设追踪航天器相对目标的初始距离为260 m，首先接近到距目标100 m处，然后再进行视线跟踪.

目标的初始轨道根数为轨道半长轴a₀=42 241 km，偏心率e₀=0，轨道倾角i₀=0 rad，升交点经度Ω₀=0 rad，近星点经度ω₀=0 rad，真近点角f₀=0 rad，初始本体坐标系与地心惯性坐标系重合，运行过程中角速度在本体坐标系中为[-0.002 5, 0.002 0, -0.002 0]^T rad/s，特征点在本体坐标系中的单位方向矢量为${\boldsymbol{n}_{\rm{b}}} = {\left[ {\sqrt 3 , - \sqrt 3 , - \sqrt 3 } \right]^{\rm{T}}}/3$，轨道机动加速度在惯性系中表示为[0.20cos (0.15t), 0.10sin (0.10t), 0.15cos (0.20t)]^T m/s².

追踪航天器初始视线倾角为0.9 rad，初始视线偏角为-1.8 rad，初始姿态角为[0.05, -0.60, 2.40]^T rad，设太阳光照方向为$\hat s = {\left[ { - \sqrt 3 ,\sqrt 3 , - \sqrt 3 } \right]^{\rm{T}}}/3$，转动惯量J_c=diag (30, 25, 20) kg·m²，每轴所能提供的最大控制加速度为5 m/s²，最大控制力矩为1 Nm，加入死区特性.

控制律参数选取为K₁=diag (0.28, 0.05, 0.10, 1.00, 1.00, 4.00), K₂=diag (6.50, 2.00, 2.60, 0.80, 0.36, 0.40)，K₃=1×10^-7，α= 0.8，λ=0.01，Δ_i=0.01.仿真时间为1 000 s.

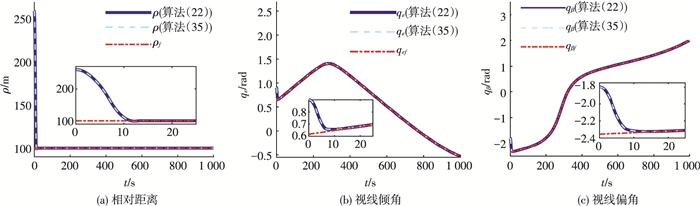
3.2 仿真结果及分析

图 2为追踪航天器在近距离跟踪指向非合作目标过程中相对轨道参数随时间变化的曲线，包括相对距离、视线倾角和视线偏角.结合局部放大图可以看出，在算法 (17) 或算法 (25) 作用下，都可以使追踪航天器在22.9 s内从相距目标260 m接近到100 m，并保持对期望轨道的跟踪.

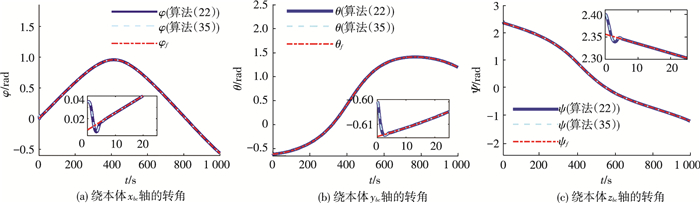
图 3为追踪航天器姿态角随时间变化曲线，结合局部放大图可以看出，在算法 (17) 或算法 (25) 作用下，都可以使姿态角在5.7 s内快速趋近于期望值，并保持在期望值附近，实现对非合作目标的指向观测.

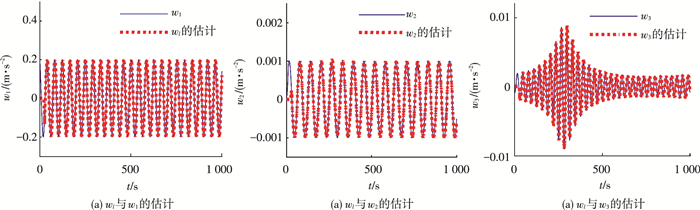
图 4为神经网络对由非合作目标加速度以及期望相对位置状态的二阶导数所引起的系统不确定性进行自适应估计的结果，由式 (12) 可知被估计量分别为${w_1} = {{\ddot \rho }_f} - {f_x}$，${w_1} = {{\ddot \rho }_f} - {f_x}$和${w_3} = {{\ddot q}_{\beta f}} + {f_z}/\left( {\rho \cos {q_\varepsilon }} \right)$.由图 4可以看出，神经网络的估计结果能够很快地收敛到被估计量，因此验证了本文所设计的RBF神经网络能够对系统不确定性进行有效地估计，进而在控制律部分进行补偿，从而提高系统的控制精度.

表 1、2为在仿真参数、控制参数相同时，算法 (17) 和算法 (25) 的控制效果对比情况，其中$\int_0^{1\;000} {\left| {{u_{ci}}} \right|{\rm{d}}t} $和$\int_0^{1\;000} {\left| {{T_{ci}}} \right|{\rm{d}}t\left( {i = x,y,z} \right)} $为整个仿真过程中追踪航天器控制作用的积累效果，e_0j(j=ρ, q_ε, q_β, φ, θ, ψ) 为轨道、姿态参数在保持跟踪过程中的幅值，∫|e_j|dt为整个仿真过程中偏差信号的积累效果.可以看出，由于算法 (25) 考虑了补偿执行机构饱和、死区等特性，在控制作用积累效果，即燃料消耗略有增加的情况下比算法 (17) 在控制精度方面有了明显的提高，其中姿态部分的提高效果更加显著.

4 结论

1) 在视线坐标系和体坐标系下分别建立了相对轨道和姿态的动力学方程，构建了姿态轨道同步控制的六自由度模型.

2) 利用RBF神经网络对系统不确定性及未知的目标运动参数进行自适应估计和补偿，采用反步法思想设计控制器使追踪航天器在有限时间内收敛到期望的相对轨道和姿态并保持.

3) 进一步考虑控制输入饱和、死区等非线性特性，对控制律进行改进，在燃料消耗略有增加的情况下明显地提高了控制精度.