高超声速滑翔飞行器指在大气层内作高速无动力滑翔的飞行器,其飞行Ma>5且具有较高的升阻比[1].高超声速滑翔飞行器的轨迹设计不仅受到热流密度、动压和终端状态等约束的严格限制[2-3],还要考虑路径点、禁飞区等实际场景中的约束[4],一直是国内外的研究热点.
轨迹优化是高超声速滑翔飞行器轨迹设计的一种重要手段.考虑到高超声速滑翔飞行器轨迹优化问题的复杂性,近年来的相关研究多采用一类同时离散控制变量和状态变量的伪谱方法[5]进行求解.文献[6]证明了高斯伪谱法转化得到的非线性规划问题的解满足间接法的一阶最优必要条件,表明伪谱法能够保证结果的最优性.文献[7]利用高斯伪谱法优化得到了高超声速滑翔飞行器的再入轨迹.文献[8]则对伪谱法加以改进,提出了一种自适应伪谱法.该方法能够自动调整配点数目和分布,降低了对初值的要求并提高计算效率.
上述文献多将重点放在如何优化得到高超声速滑翔飞行器在各种过程约束下到达指定点的轨迹上.但在实际场景中,高超声速滑翔飞行器必须面对导弹防御系统的挑战,这就需要在轨迹的设计中考虑禁飞区等更复杂的约束条件[4],以利用飞行器自身的机动能力规避拦截区.在规避禁飞区方面,文献[9]基于一定的倾斜角变化规律优化得到了高超声速滑翔飞行器规避拦截区的再入轨迹.文献[10]将一种倾侧角反转逻辑改进而来的侧向几何制导逻辑用于预测制导,实现了对禁飞圆的规避.文献[11]则在一个相对较小的时间尺度下忽略终端速度和射程约束,基于动态逆的思想设计了高超声速滑翔飞行器的摆动式机动突防弹道.以上对机动规避轨迹设计的研究大都在一个较小的时间尺度内考虑问题,无法得到高超声速滑翔飞行器的全程飞行轨迹.
针对高超声速滑翔飞行器机动规避轨迹的优化问题,本文通过引入拼接点将轨迹分为若干段,并利用能够处理多阶段优化问题的自适应伪谱法进行轨迹的优化设计,以得到满足各项约束条件的机动规避轨迹,最后通过仿真验证了该方法的有效性.
1 轨迹优化设计模型 1.1 动力学模型考虑地球自转和扁率,在半速度坐标系中建立高超声速滑翔飞行器三自由度运动方程[12]如下:
| $ \left\{ \begin{array}{l} \dot r = v\sin \theta ,\\ \dot \varphi = \frac{{v\cos \theta \sin \psi }}{{r\cos \varphi }},\\ \dot \lambda = - \frac{{v\cos \;\theta \cos \psi }}{{r\cos \varphi }},\\ \dot v = - \frac{D}{m} + {g_r}\sin \theta + \\ \;\;\;\;\;\;{g_{{\omega _e}}}\left( {\cos \psi \cos \theta \cos \varphi + \sin \theta \sin \varphi } \right) - \\ \;\;\;\;\;\;\omega _e^2r\left( {\cos \varphi \sin \varphi \cos \psi \cos \theta - {{\cos }^2}\varphi \sin {\theta _{\rm{T}}}} \right),\\ \dot \theta {\rm{ = }}\frac{{L\cos \sigma }}{{mv}} + \frac{{{g_r}\cos \theta }}{v} - \\ \;\;\;\;\;\frac{{{g_{{\omega _e}}}}}{v}\left( {\cos \varphi \cos \psi \sin \theta - \sin \varphi \cos \theta } \right) + \\ \;\;\;\;\;\frac{{\omega _e^2r}}{v}\left( {\cos \varphi \sin \varphi \cos \psi \sin \theta + {{\cos }^2}\varphi \cos \theta } \right) - \\ \;\;\;\;\;2{\omega _e}\cos \varphi \sin \psi + \frac{{v\cos \theta }}{r},\\ \dot \psi = - \frac{{L\sin \sigma }}{{mv\cos \theta }} - \frac{{{g_{{\omega _e}}}\cos \varphi sin\psi }}{{v\cos \theta }} + \\ \;\;\;\;\;\;\;\omega _e^2r\frac{{\cos \varphi \sin \varphi \sin \psi }}{{v\cos \theta }} + \\ \;\;\;\;\;\;\;\frac{{2{\omega _e}}}{{\cos \theta }}\left( {\cos \varphi \cos \psi \sin \theta - \sin \varphi cos\theta } \right) + \\ \;\;\;\;\;\;\;\frac{{v\tan \varphi \cos \theta \sin \psi }}{r}. \end{array} \right. $ |
式中:v为高超声速滑翔飞行器相对地球表面的速度;m为飞行器质量;θ为当地速度倾角;ψ为航迹偏航角;σ为倾侧角;r为地心距;φ、λ分别为纬度和经度;ωe为地球自转角速度;gr、gωe分别为引力加速度在地心矢径和地球自转角速度方向的分量;L、D分别为升力和阻力,具体表达式为
| $ \left\{ \begin{array}{l} {\rm{L = }}\frac{1}{2}\rho {v^2}{C_{\rm{L}}}S,\\ {\rm{D}} = \frac{1}{2}\rho {v^2}{C_{\rm{D}}}S. \end{array} \right. $ |
式中:S为特征面积;CL、CD分别为升力系数和阻力系数,由飞行器的攻角和Ma决定[13];ρ为大气密度,采用指数模型ρ=ρ0e-h/hs.
1.2 约束条件 1.2.1 终端约束要求高超声速滑翔飞行器以足够大的速度到达指定目标点,因此终端约束可表示为
| $ \left\{ \begin{array}{l} {r_{\rm{f}}} = {r_{\rm{d}}},\\ {\varphi _{\rm{f}}} = {\varphi _{\rm{d}}},\\ {\lambda _{\rm{f}}} = {\lambda _{\rm{d}}},\\ {v_{\rm{f}}} \ge {v_{{\rm{dmin}}}}. \end{array} \right. $ |
式中:下标f为实际的终端量,下标d为期望的终端量;下标dmin为期望终端量的最小值.
1.2.2 过程约束过程约束包括热流密度Q、动压q和过载n.
| $ \left\{ \begin{array}{l} Q = K{\left( {\frac{\rho }{{{\rho _0}}}} \right)^a}{\left( {\frac{v}{{{v_c}}}} \right)^b} \le {Q_{\max }},\\ q = \frac{1}{2}\rho {v^2} \le {q_{\max }},\\ n = \frac{{\sqrt {{{\rm{L}}^2} + {{\rm{D}}^2}} }}{{m{g_0}}} \le {n_{\max }}. \end{array} \right. $ |
式中:下标max为最大值;K, a, b分别为相关常数;Vc为环绕速度,其具体表达式为
此外,为了保证高超声速滑翔飞行器的飞行高度平缓下降,还需要加入平衡滑翔约束[14-15].由于地球扁率和自转对高超声速滑翔飞行器飞行高度变化的影响较小,为简化表达式,假设地球为不旋转圆球,平衡滑翔约束可表示为
| $ \frac{{R_0^2}}{{{r^2}}}{g_0} - \frac{{{v^2}}}{r} - \frac{L}{m}\cos \sigma = 0. $ |
禁飞区为无穷高柱形区域,其半径为Rmax.
1.2.4 控制量约束高超声速滑翔飞行器轨迹的控制量为攻角α和倾侧角σ,其取值应限定在一定范围内为
| $ \left\{ \begin{array}{l} {0^ \circ } \le \alpha \le {20^ \circ },\\ - {45^ \circ } \le \sigma \le {45^ \circ }. \end{array} \right. $ |
对于高超声速滑翔飞行器来说,其滑翔飞行段应在满足各项约束的前提下减小气动加热并保持弹道平滑,因此优化目标函数为
| $ J = \int_{{t_0}}^{{t_{\rm{f}}}} {Q{\rm{d}}t} + k\int_{{t_0}}^{{t_{\rm{f}}}} {{{\dot \psi }^2}{\rm{d}}t} . $ |
式中:t0、tf分别为初始时刻和终止时刻;k为比例系数,用于调节优化指标中即弹道平滑的权重.
优化目标中气动加热与弹道平滑的指标存在一定的一致性,弹道越不平滑,需要越多的气动力进行横向机动,相应的气动加热也会增加,从而损耗更多的飞行能量,同样条件下飞行器能够达到的最大航程也会降低;但也存在一定的矛盾性,在不考虑弹道平滑指标时,为降低气动加热,仿真结果中飞行器会以更大的半径转弯以对禁飞区进行规避.因此在选取比例系数时需要折衷考虑.
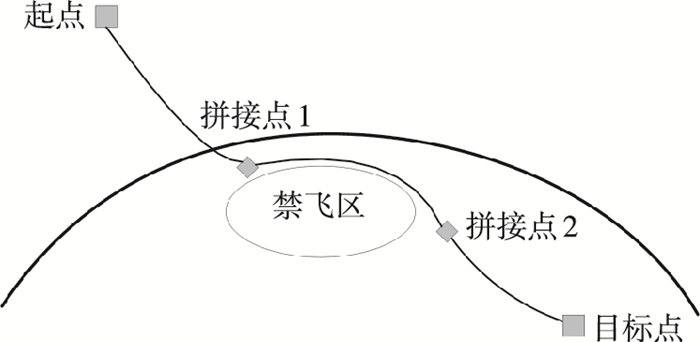
2 基于拼接的机动规避轨迹传统的平衡滑翔轨迹较为平滑且基本保持在同一纵平面内,易于跟踪和拦截而不利于突防.为提高飞行器的突防能力,可引入拼接点将轨迹分为多段进行优化设计,这样就利用拼接点的分布在平衡滑翔轨迹中引入横向机动从而绕开禁飞区,如图 1所示.
|
图 1 机动规避轨迹示意 Figure 1 Sketch map of maneuver evasion trajectory |
拼接点的分布直接影响轨迹的形态和优化结果,其位置的选择是一个迭代的过程.首先需要先根据高超声速飞行器的机动能力确定其可达区域,再根据可达区域的情况及禁飞区的形状和分布确定拼接点的数目和大致位置,一般位于禁飞区的外沿,而高度则依靠伪谱法的收敛能力进行调整.然后对轨迹进行优化,观察优化结果中并据此调整拼接点的位置直至优化结果满足要求.
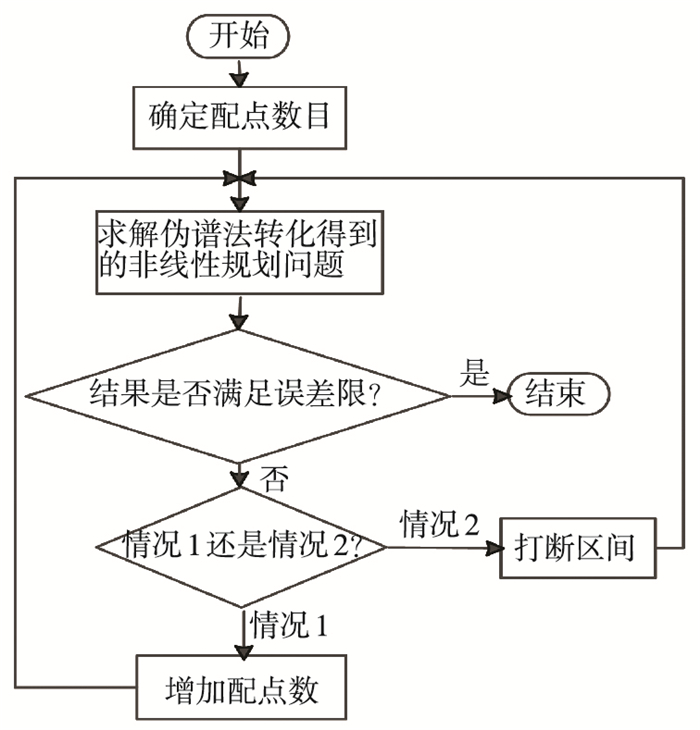
3 自适应伪谱法基于拼接的机动规避轨迹优化需要在考虑整个轨迹优化的同时处理好轨迹在拼接点处的衔接问题.伪谱法同时离散状态量和控制量的做法使得只需加入拼接点处的物理量约束即可处理这一问题.为达到更好的优化效果,选用可以自动调整配点分布的hp自适应伪谱法[8]规避轨迹的优化设计.hp自适应伪谱法在每次完成优化计算后都会检查离散点的数目与分布情况,并据此调整区间和离散点的数目与分布情况,然后进行下一次的优化计算,直至残差满足要求为止,其流程如图 2所示.
|
图 2 自适应伪谱法流程 Figure 2 Flow chart of adaptive pseudospectral method |
此外需保证拼接点处物理量的平滑衔接为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{X}}_{i + 1}}\left( {t_0^{\left( {t + 1} \right)}} \right) - {\mathit{\boldsymbol{X}}_i}\left( {t_e^{\left( i \right)}} \right) = 0,\\ {\mathit{\boldsymbol{U}}_{i + 1}}\left( {t_0^{\left( {t + 1} \right)}} \right) - {\mathit{\boldsymbol{U}}_i}\left( {t_e^{\left( i \right)}} \right) = 0. \end{array} \right. $ |
式中:X为状态列向量;U为控制列向量;i=1, 2, …,L-1为区间序号;t0(i+1)为第i+1个区间的初始时刻, te(i)为第i个区间的终止时刻.
4 仿真分析仿真的初始条件和各类约束取值见表 1,高超声速滑翔飞行器参数参考文献[13].
| 表 1 初始条件和约束 Table 1 Initial conditions and constraints |
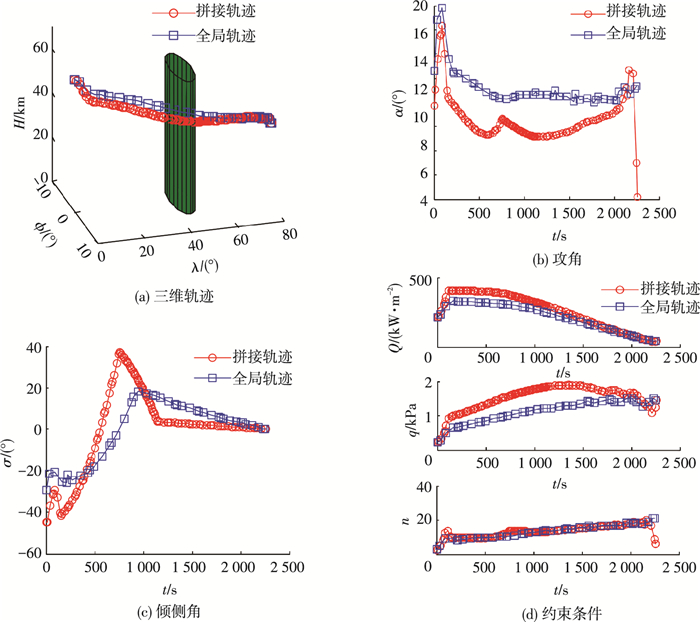
考虑单个禁飞区的情况,禁飞区中心位于 (0°N, 45°E),半径为500 km.目标点为 (0°N, 84°E).选择两个拼接点 (4.4°N, 37°E) 和 (4.2°N, 53°E),拼接优化与全局优化的结果如图 3所示.
|
图 3 算例1结果 Figure 3 Results of case 1 |
计算所使用的计算机CPU为Corei3-4130,主频3.4 GHz,内存4 GB,程序运行环境为Matlab R2013a,计算耗时6.94 s.
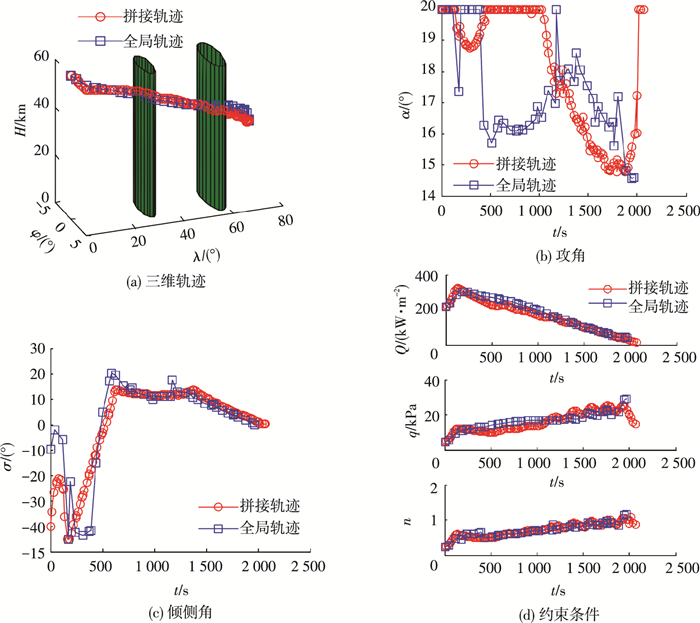
4.2 算例2考虑两个禁飞区的情况,第1个禁飞区中心位于 (0°N, 30°E),半径为300 km;第2个禁飞区中心位于 (0°N, 57°E),半径为400 km;目标点为 (0°N, 72.4°E).选择两个拼接点 (3.1°N, 30°E) 和 (3.6°N, 57°E),拼接优化与全局优化的结果如图 4所示.
|
图 4 算例2结果1 Figure 4 Results 1 of case 2 |
优化计算环境与算例1相同,用时9.15 s.
将两个拼接点位置改为 (3.1°N, 30°E) 和 (3.6°S, 57°E),,结果如图 5所示.
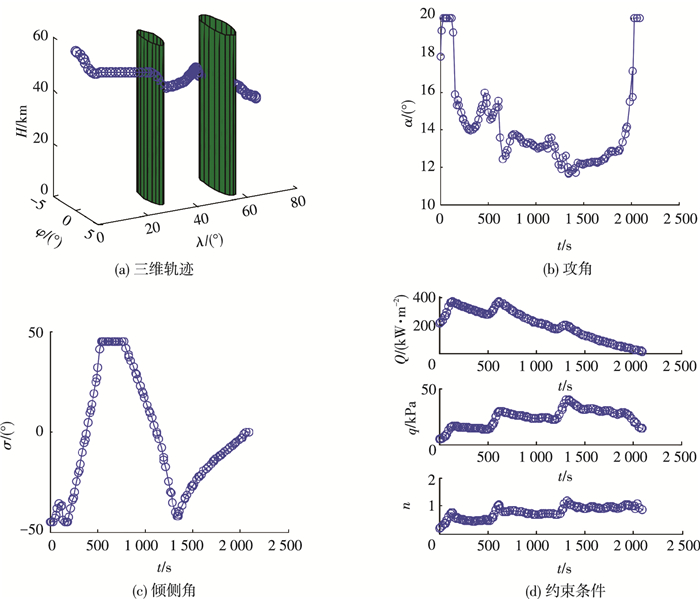
|
图 5 算例2结果2 Figure 5 Results 2 of case 2 |
优化计算环境与算例1相同,用时7.84 s.
4.3 结果分析算例1和算例2在引入两个拼接点的情况下分别优化得到了一个禁飞区和两个禁飞区情况下的机动规避轨迹并与全局优化的结果进行了对比.结果表明,飞行器在满足各项过程约束的情况下通过横向的机动成功规避了禁飞区且满足终端状态的要求,拼接点处状态量和控制量衔接平滑.由于拼接点的分布,拼接轨迹与全局轨迹存在着一定的差别,索命拼接点能够在一定程度上控制拼接轨迹的形态,虽然单纯从满足约束并到达目标点的角度看拼接轨迹是一种次优的轨迹,但不同的拼接点分布可以得到不同的拼接平衡滑翔轨迹.算例2的两个结果就以不同的拼接点分布得到了不同的拼接平衡滑翔轨迹,其中在结果1中飞行器以一个大的横向机动规避了两个禁飞区,而在结果2中飞行器以一个S形的横向机动相继规避了两个禁飞区,分别对应文献[9]中的半圆机动和单S机动,这也是全局优化无法做到的.实际上拼接点在上述方法中起到了在优化时引入额外控制变量的作用,通过拼接点的选择可以设计带有特定机动动作的轨迹.这表明即使在不存在禁飞区的情况下,也可以利用拼接点来得到带有较大横向机动的轨迹以达到突防的目的.
5 结论1) 通过引入拼接点将轨迹分为若干段,结合自适应伪谱法提出了一种基于拼接的高超声速滑翔飞行器机动规避轨迹优化设计方法.
2) 仿真结果表明, 设计得到的高超声速滑翔飞行器机动规避轨迹在满足各种约束条件的情况下有效规避了禁飞区,准确到达目标点且计算耗时较少.
3) 拼接点的位置起到了控制变量的作用,机动规避轨迹的形态受拼接点选择的影响,通过调整拼接点的位置可以得到不同的机动规避轨迹.这种设计方法能够设计得到横向大幅复杂机动轨迹.
| [1] |
李惠峰.
高超声速飞行器制导与控制技术[M]. 北京: 中国宇航出版社, 2012: 1-26.
LI Huifeng. Guidance and control technology of hypersonic vehicle[M]. Beijing: China Astronautic Publishing House, 2012: 1-26. |
| [2] | SHEN Zuojun, LU Ping. Onboard generation of three-dimensional constrained entry trajectories[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(1): 111-121. DOI: 10.2514/2.5021 |
| [3] |
刘鹏, 谷良贤. 高超声速飞行器动态输出反馈最优跟踪控制[J].
哈尔滨工业大学学报, 2011, 43(7): 131-134.
LIU Peng, GU Liangxian. Dynamic output feedback based optimal tracking for hypersonic flight vehicles[J]. Journal of Harbin Institute of Technology, 2011, 43(7): 131-134. DOI: 10.11918/j.issn.0367-6234.2011.07.027 |
| [4] | JORRIS T R, COBB R G. Three-dimensional trajectory optimization satisfying waypoint and no-fly zone constraints[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(2): 551-572. DOI: 10.2514/1.37030 |
| [5] | ROSS I M, KARPENKO K. A review of pseudospectral optimal control: from theory to flight[J]. Annual Reviews in Control, 2012, 36(2): 182-197. DOI: 10.1016/j.arcontrol.2012.09.002 |
| [6] | HUNTINGTON G T. Advancement and analysis of a gauss pseudospectral transcription for optimal control[D]. Cambridge:Massachusetts Institute of Technology, 2007. |
| [7] |
雍恩米, 唐国金, 陈磊. 基于Gauss伪谱方法的高超声速飞行器再入轨迹快速优化[J].
宇航学报, 2008, 29(6): 155-158.
YONG Enmi, TANG Guojin, CHEN Lei. Rapid trajectory optimization for hypersonic reentry vehicle via gauss pseudospectral method[J]. Journal of Astronautics, 2008, 29(6): 155-158. DOI: 10.3873/j.issn.1000-1328.2008.06.016 |
| [8] | DARBY C L, HAGER W W, RAO A V. An hp-adaptive pseudospectral method for solving optimal control problems[J]. Optimal Control Applications and Methods, 2011, 32(4): 476-502. DOI: 10.1002/oca.957 |
| [9] |
张科南, 周浩, 陈万春. 高超声速飞行器多约束多种机动突防模式弹道规划[J].
弹道学报, 2012, 24(3): 85-90.
ZHANG Ke'nan, ZHOU Hao, CHEN Wanchun. Trajectory planning for hypersonic vehicle with multiple constraints and multiple maneuvering penetration strategies[J]. Journal of Ballistics, 2012, 24(3): 85-90. DOI: 10.3969/j.issn.1004-499X.2012.03.017 |
| [10] |
王青, 莫华东, 吴振东, 等. 考虑禁飞圆的高超声速飞行器再入预测制导[J].
哈尔滨工业大学学报, 2015, 47(2): 104-109.
WANG Qing, MO Huadong, WU Zhendong, et al. Predictive reentry guidance for hypersonic vehicles considering no-fly zone[J]. Journal of Harbin Institute of Technology, 2015, 47(2): 104-109. DOI: 10.11918/j.issn.0367-6234.2015.02.019 |
| [11] |
谢愈, 刘鲁华, 汤国建, 等. 高超声速滑翔飞行器摆动式机动突防弹道设计[J].
航空学报, 2011, 32(12): 2174-2181.
XIE Yu, LIU Luhua, TANG Guojian, et al. Weaving maneuver trajectory design for hypersonic glide vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(12): 2174-2181. |
| [12] |
赵汉元.
飞行器再入动力学和制导[M]. 长沙: 国防科技大学出版社, 1997: 452-454.
ZHAO Hanyuan. Dynamics and guidance of reentry vehicle[M]. Changsha: Press of National University of Defense Technology, 1997: 452-454. |
| [13] | PHILLIPS T H.A common aero vehicle (CAV) model, description, and employment guide[R].[S.I.]:Schafer Corporation for AFRL and AFSPC, 2003. |
| [14] | XU Mingliang, CHEN Kejun, LIU Luhua, et al. Quasi-equilibrium glide adaptive guidance for hypersonic vehicles[J]. Science China Technology Science, 2012, 55(3): 856-866. DOI: 10.1007/s11431-011-4727-z |
| [15] |
卢宝刚, 傅瑜, 崔乃刚, 等. 基于拟平衡滑翔的数值预测再入轨迹规划算法[J].
哈尔滨工业大学学报, 2015, 47(1): 14-19.
LU Baogang, FU Yu, CUI Naigang, et al. Numerical prediction method of reentry trajectory planning based on quasi equilibrium glide condition[J]. Journal of Harbin Institute of Technology, 2015, 47(1): 14-19. DOI: 10.11918/j.issn.0367-6234.2015.01.003 |
 2017, Vol. 49
2017, Vol. 49


