2. 上海宇航系统工程研究所,上海 201108
2. Aerospace System Engineering Shanghai, Shanghai 201108, China
太阳帆是依靠反射太阳光而不需要携带燃料的航天器.根据展开方式的不同,太阳帆结构体系可分为两大类:利用自旋离心力展开的结构体系和支撑伸展臂牵引帆面展开的结构体系.本文选取由对角支撑伸展臂牵引帆面展开的结构体系的太阳帆作为研究对象,豆荚杆为支撑构件,Kapton薄膜为帆面材料.展开过程为拉扁/压扁缠绕的豆荚杆沿对角伸展,恢复透镜式截面形状,展开设计简单、可靠性高.
在国内,罗超等[1]认为太阳帆结构设计是总体设计的重要内容,结构是功能实现的基础,需要将帆体结构设计与姿态控制方案设计相结合.崔乃刚等[2]对柔性太阳帆航天器动力学建模和姿态控制进行了研究,认为对角伸展的正方形太阳帆采用三轴姿态控制方案,无论采用帆面转动法、质心偏移法还是帆体参数调整法,皆基于刚性假设,未考虑太阳帆柔性因素及预应力导入刚化效应,而李俊峰等[3]研究表明太阳帆姿态、结构会改变推力大小、方向从而使轨道控制失真.陈集丰等[4]就轻质太阳帆结构强度分析等方面开展研究,分析了螺旋桨形的太阳帆结构体系.黄小琦等[5]对太阳帆折叠方式和展开过程进行了研究.陈务军等[6-10]对太阳帆薄壁CFRP豆荚杆拉压扁、缠绕和展开过程进行了深入研究,并进行了轴压屈曲分析、模态分析以及豆荚杆工作状态下热效应研究.在国外,Wie[11]认为采用三轴姿态控制方案,对角豆荚杆作为俯仰轴和偏航轴,相较于自旋稳定姿态控制方案更便捷高效.Sickinger等[12]对太阳帆展开状态下的膜面应力、褶皱分布情况和复合材料薄壁豆荚杆在轴压、弯矩组合作用下结构失效的包络图进行了研究.Wawrzyniak等[13]对太阳帆星际航行轨道设计进行了研究,提出了“turn-and-hold”轨道设计策略.Johnson等[14]对Nano Sail-D太阳帆进行了地面展开试验,对展开过程和豆荚杆性能进行了研究.Rizvi等[15]对姿轨耦合进行了深入研究.
目前关于太阳帆结构设计的研究中,膜面应力导入方式对应力分布的影响及膜面应力大小对太阳帆整体结构刚度的影响研究较少.本文以对角伸展太阳帆为研究对象,首先阐述了此类太阳帆导入膜面应力的重要性和导入张力的合理范围,按照执行部件的不同,介绍了膜面应力导入的3种不同方式;然后采用有限元软件ABAQUS分别对3种方式导入膜面应力的太阳帆进行了结构分析,模拟不同膜面应力和光压的工况,获得膜面应力和豆荚杆轴压之间的关系以及光压与推力、悬臂荷载之间的关系;最后对比分析了不同导入方式对膜面应力分布以及光压作用下不同膜面应力对帆面形态和结构刚度的影响.由于光压作用远小于重力作用,实际太阳帆工作处于失重状态,且所关心的膜面应力场、豆荚杆轴压值、帆面褶皱分布和幅值等均不易试验获得,故先采用有限元软件进行模拟分析.
1 太阳帆膜面应力及其导入方式太阳帆整体刚度越大越有利于姿态控制,通过施加膜面应力可以在不增加质量前提下提高帆面刚度、结构整体刚度及姿态保持能力,充分发挥超轻柔性帆面作用,且通过导入膜面应力可以减小由光压压力作用中心与质心不一致产生的附加弯矩所引起的帆面扰动,使膜面更平整,反射效率更高.另一方面,导入张力将使对角豆荚杆产生轴压,膜面应力越大,轴压越大,而对角豆荚杆为细长杆件,受压容易发生轴压屈曲,因此膜面应力理论最大值为其产生的豆荚杆轴压力恰好到达豆荚杆屈曲承载力值,实际设计过程中应当考虑适当的安全系数以取得其合理范围.
按照导入张力部件的不同,膜面应力的导入方式主要有:1) 通过对角豆荚杆导入,在豆荚杆伸长到位后再伸长一定值;2) 通过太阳帆膜面周边的悬链导入,当豆荚杆伸长到位后保持不动,通过电机张紧周边悬链;3) 通过帆面本身导入,考虑薄膜的裁切效应,使薄膜在对角豆荚杆伸长到位同时产生所需的应力值.不同实现方式对膜面应力的分布有一定影响.聚酰亚胺材料由于制备工艺的不同,其力学性能差异较大,因此针对太阳帆的不同部位,选用的材料也不尽相同.尤其是受力较大位置,薄膜材料应该经过处理以防止撕裂,因此掌握膜面应力的分布对于结构优化设计、防止局部撕裂具有重要意义.
2 太阳帆结构数值分析模型采用有限元软件ABAQUS,以文献[13]中介绍的欧洲航天局和德国宇航中心1999年制作的20 m×20 m太阳帆建立有限元模型, 如图 1所示.豆荚杆为支撑构件,Kapton薄膜为膜面材料,薄膜周边有悬链,通过豆荚杆伸长,带动太阳帆展开.

|
图 1 太阳帆有限元模型 Figure 1 FEM model of solar sail |
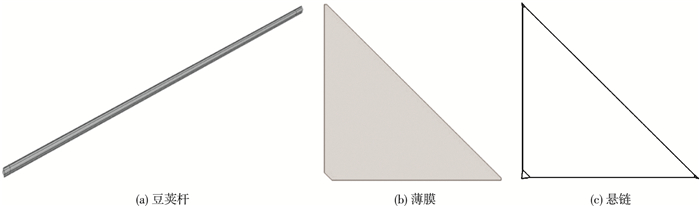
模型有豆荚杆、薄膜和薄膜周边悬链3种部件组成,悬链部件的基本特性为wire,豆荚杆和薄膜基本特性为shell,如图 2所示.
|
图 2 模型的组成部件 Figure 2 Parts of the model |
豆荚杆长度为14 m,截面如图 3所示,截面由中间圆弧段、两边圆弧段和两边直线段组成,截面尺寸141 mm×70 mm,截面积99.96 mm2,回转半径ix、iy分别为20.36、39.50 mm,由上、下两肋片两边黏合而成,薄壁对称透镜状,上、下片采用由12层碳纤维增强环氧树脂预浸料复合材料铺成,每层厚度为0.025 mm,铺设角度为[+45/-45/0/-45/+45/0]2s,预浸料铺层力学性能见表 1.豆荚杆按照在薄膜平面内能提供较大的弯曲刚度的方式放置.

|
图 3 薄壁豆荚杆横截面 Figure 3 Cross-section of the thin-walled lenticular CFRP boom |
| 表 1 预浸料铺层力学性能 Table 1 Mechanical properties of prepreg ply |
悬链为钢丝绳,直径为0.5 mm,密度为7.8 g/cm3,弹性模量取160 GPa,泊松比为0.3,采用truss单元 (T3D2).薄膜厚度为0.007 5 mm,密度为5 g/cm3,弹性模量2.842 GPa,泊松比0.38,单元类型为S3.悬链与薄膜边缘绑定 (tie),在模型中心和豆荚杆末端设置参考点,将豆荚杆两端各分割出200 mm,靠近中心处豆荚杆分割段、薄膜直角处短边与中心参考点绑定,形成刚体 (rigid body).悬臂端豆荚杆分割段、薄膜45°角处短边与豆荚杆末端参考点绑定,形成刚体.边界条件为将中心参考点固支.
膜面应力产生刚度,抵抗面外荷载.随着薄膜张力的增大,豆荚杆轴向压力增大.当豆荚杆轴向压力增大到一定值时,豆荚杆发生轴压屈曲.因此,为确定薄膜张拉所需的合理张力范围,需首先对悬臂豆荚杆进行线性特征值轴压屈曲分析.在面外荷载的作用下,悬臂豆荚杆将受到垂直于端部截面的荷载,亦可能发生悬臂屈曲,因此也需对悬臂豆荚杆的进行悬臂屈曲分析.然后分别对3种方式导入膜面应力的对太阳帆整体结构特性进行分析,分析其在不同面内张力、不同面外压力的条件下,膜面褶皱的分布情况和皱幅、豆荚杆的端部位移.
3 悬臂豆荚杆屈曲分析 3.1 豆荚杆轴压屈曲分析图 2(a)部件,在豆荚杆两端截面中心布置参考点,将两端的分割段与中心参考点绑定,一端参考点施加固支边界条件,另一端沿豆荚杆轴向作用单位荷载1 N,如图 4所示,进行轴压线性特征值屈曲 (buckling) 分析,采用Lanczos法求解特征值方程,提取前20阶.

|
图 4 轴压线性特征值屈曲分析 Figure 4 Linear eigenvalue buckling analysis under axial compression |

|
图 5 前6阶屈曲模态 Figure 5 The first six linear buckling modes |
模型第1、3、4、6阶为模型绕豆荚杆截面X对称轴发生屈曲时的前4阶模态,模型第2、5阶为模型绕豆荚杆截面Y轴发生屈曲时的前两阶模态.取模型第1阶计算临界屈曲荷载为Pcr=λP=1×7.388 =7.388 N.
3.2 豆荚杆悬臂屈曲分析将另一端作用单位荷载1 N改为沿着豆荚杆截面Y对称轴,如图 6所示,其余如轴压屈曲分析,进行悬臂弯曲屈曲分析.

|
图 6 弯曲线性特征值屈曲分析 Figure 6 Linear eigenvalue buckling analysis under bending load |
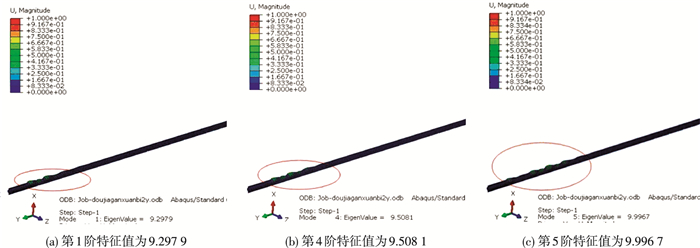
由于结构对称,奇数阶与其后偶数阶模态关于中性面对称.图 7给出线性弯曲屈曲分析第1阶、第4阶、第5阶屈曲振型,均为局部屈曲振型,上下片两端黏结直线段和中间圆弧段发生局部屈曲,屈曲发生在豆荚杆悬臂梁固定端附近.第1阶、第4阶、第5阶特征值分别为9.297 9、9.508 1、9.996 7,取第1阶模态计算临界屈曲荷载为Pcr=λP=1×9.297 9=9.297 9 N.
|
图 7 第1、4、5阶弯曲屈曲模态 Figure 7 The first, fourth, fifth bending-buckling modes |
分别对采用3种方式导入膜面应力的太阳帆进行整体结构特性分析,采用非线性静力分析模拟不同膜面应力和不同光压工况下的结构响应,分两个阶段施加荷载:1) 施加膜面应力,采用控制温度场变化的方法给薄膜施加张力.方式1为使豆荚杆升温膨胀来实现膜面应力导入,方式2为使悬链降温收缩张紧来实现膜面应力导入,方式3为直接通过薄膜降温收缩来实现膜面应力导入;2) 施加光压.
薄膜横向变形引起纵向应力变化,改变了结构的刚度矩阵,从而影响结构的固有频率,产生应力刚化效应,属于几何非线性过程,需考虑非线性,最后对模拟结果进行单元有效性和网格收敛性验证.
计算表明,薄膜膜面应力与豆荚杆轴向压力之间的关系与膜面应力导入方式几乎无关,光压作用下太阳帆推力、悬臂荷载及悬臂端最大位移与应力导入方式亦几乎无关.不同膜面应力与豆荚杆轴向压力关系,见表 2.通过控制膜面光压,获得不同膜面压力和豆荚杆悬臂荷载、悬臂端最大位移的关系,见表 3.其中1天文单位 (1 AU) 处的太阳辐射压强P=4.56×10-6 Pa.
| 表 2 不同膜面应力下对应的轴向压力值 Table 2 Corresponding axil compression values under different membrane stresses |
| 表 3 不同膜面光压力下对应的推力、悬臂荷载、悬臂位移值 Table 3 Corresponding thrust, cantilever load and displacement values under different light pressure of the membrane |
根据豆荚杆轴压屈曲分析,豆荚杆轴压临界屈曲荷载7.388 N,结合表 2,可确定膜面应力合理范围是不超过0.17 MPa.豆荚杆绕Y轴的悬臂屈曲荷载为9.297 9 N,远大于表 3中悬臂荷载,说明在光压作用下,豆荚杆不会发生悬臂屈曲.
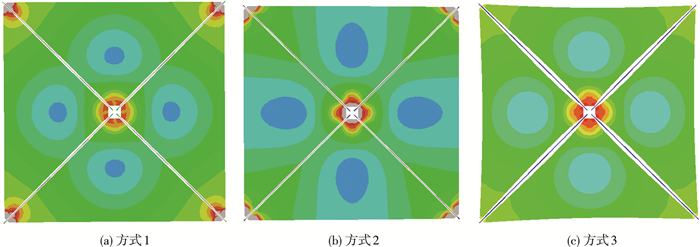
分别采用3种方式导入膜面应力0.17 MPa,得到膜面应力分布如图 8所示.然后施加光压,在3 AU光压作用下位移分布如图 9所示.
|
图 8 导入膜面应力0.17 MPa时应力云图 Figure 8 Stress nephogram under 0.17 MPa membrane stress |

|
图 9 AU光压作用下位移云图 Figure 9 Displacement nephogram under 3 AU light pressure |
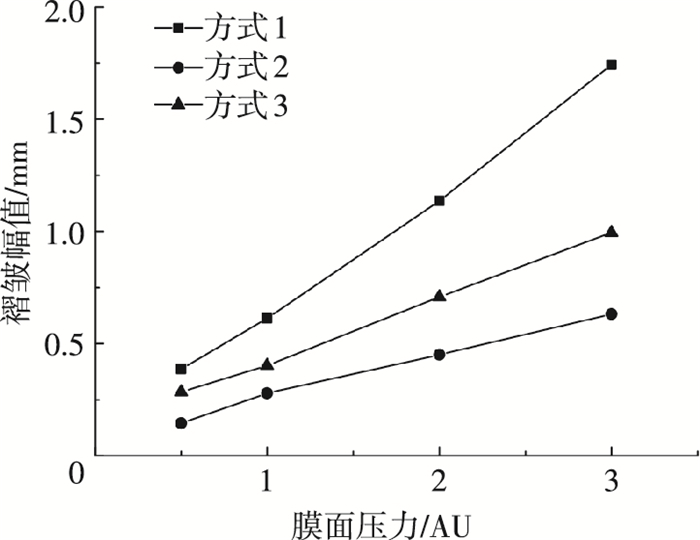
图 8中应力分布可看出,3种方式导入的膜面应力分布大体规律是一致的,局部略有区别.太阳帆三角形膜片中间处应力较小,3个角落处应力较大,应当进行局部加强.光压作用下3种方式导入膜面应力的太阳帆变形如图 9所示,方式1产生的褶皱较少较细,分布与三角形薄膜的两脚处;方式2产生的褶皱较密,且均布于三角形薄膜;方式3产生的褶皱较明显,分布于三角形薄膜两角,这与文献[13]中所得到膜面褶皱分布情况一致.膜面褶皱产生原理如下:在没有面外太阳光压时,膜面应力分布在平面内较均匀,无面外位移;在太阳作用下,豆荚杆杆端受到集中荷载作用下为悬臂梁,发生弯曲,膜面应力作用将发生重分布,局部应力将减小,在光压作用下将产生面外凹陷形成褶皱,以增大面外刚度.不同膜面光压力和褶皱幅值关系曲线如图 10所示.
|
图 10 不同膜面光压力下褶皱幅值 Figure 10 Amplitude of crease under different light pressure |
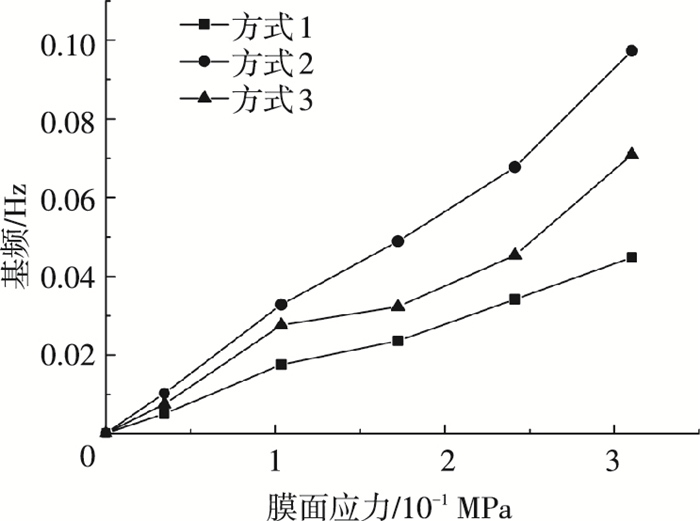
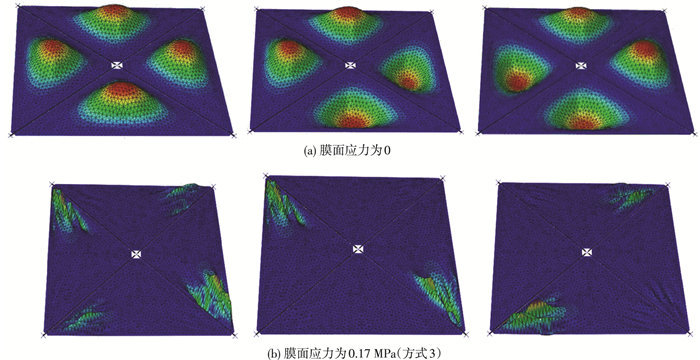
为了探究不同膜面应力大小以及导入方式对太阳帆刚度的影响,比较不同膜面应力下的基频.分析过程为:1) 膜面应力施加;2) 采用Frequency对结构进行频率提取.不同膜面应力下的前三阶振型如图 11所示,不同导入方式膜面应力与基频关系如图 12所示.
|
图 11 不同膜面应力下基频值 Figure 11 Frequecy under different membrane stress |
|
图 12 前3阶振型 Figure 12 The first three mode shapes |
观察前20阶振型,当膜面应力为0时,结构基频几乎为0,振型表现为整体振型.当施加有膜面应力时,薄膜由于应力分布的不均匀,局部刚度较小,3种膜面应力导入方式均表现为膜面局部振型.随着膜面应力的增加,结构基频显著变大.
4 结论1) 太阳帆尺寸大,薄膜厚度薄,结构刚度极小,导入膜面应力可以在不增加质量的前提下提高结构刚度,同时膜面初始张力会对支撑豆荚杆产生轴向压力,豆荚杆长细比较大,容易发生轴压屈曲,因此膜面应力亦不宜过大.
2) 在光压作用下,悬臂豆荚杆不发生悬臂屈曲.可通过豆荚杆轴压屈曲分析,确定豆荚杆临界屈曲荷载,再考虑相应安全系数后,从而可以确定可导入膜面应力的最大值.
3) 太阳帆计算分析分为两阶段.第1阶段为导入膜面应力,第2阶段为施加膜面光压力.不同导入方式对膜面应力分布有一定的影响,在光压作用下太阳帆薄膜将会产生褶皱,不同导入方式对褶皱分布也有影响.
4) 通过不同膜面应力作用下,太阳帆基频变化可看出,膜面应力对太阳帆的整体结构刚度影响较大,采用不同方式导入膜面应力对太阳帆结构刚度也有影响.膜面应力越大,基频越大,整体结构越刚,越有利于整体运动的控制.
| [1] |
罗超, 郑建华, 高东. 太阳帆航天器的轨道动力学和轨道控制研究[J].
宇航学报, 2009, 30(6): 2111-2117.
LUO Chao, ZHENG Jianhua, GAO Dong. Study on orbit dynamics and control of solar-sail spacecraft[J]. Journal of Astronautics, 2009, 30(6): 2111-2117. DOI: 10.3873/j.issn.1000-1328.2009.06.010 |
| [2] |
崔乃刚, 刘家夫, 荣思远. 柔性太阳帆航天器动力学建模与姿态控制[J].
哈尔滨工业大学学报, 2011, 43(7): 1-5.
CUI Naigang, LIU Jiafu, RONG Siyuan. Study on dynamics modeling and attitude control of flexible solar sail spacecraft[J]. Journal of Harbin Institute of Technology, 2011, 43(7): 1-5. DOI: 10.11918/j.issn.0367-6234.2011.07.001 |
| [3] |
李俊峰, 宝音贺西. 深空探测中的动力学与控制[J].
力学与实践, 2007, 29(4): 1-8.
LI Junfeng, BAOYIN Hexi. Dynamics and control in deep space exploration[J]. Mechanics in Engineering, 2007, 29(4): 1-8. DOI: 10.3969/j.issn.1000-0879.2007.04.001 |
| [4] | 陈集丰, 段德高, 乌修金. 太阳帆结构分析[J]. 宇航学报, 1996, 17(3): 77-80. |
| [5] |
黄小琦, 王立, 刘宇飞, 等. 大型太阳帆薄膜折叠及展开过程数值分析[J].
中国空间科学技术, 2014, 34(4): 31-38.
HUANG Xiaoqi, WANG Li, LIU Yufei, et al. Numerical analysis on the deployment and folding process of large-scale solar sail membrane[J]. Chinese Space Science and Technology, 2014, 34(4): 31-38. DOI: 10.3780/j.issn.1000-758X.2014.04.005 |
| [6] |
李瑞雄, 陈务军, 付功义, 等. 透镜式缠绕肋压扁缠绕过程数值模拟分析[J].
宇航学报, 2011, 32(1): 224-231.
LI Ruixiong, CHEN Wujun, FU Gongyi, et al. Numerical simulation of flattening and wrapping process of lenticular wrapped-rib[J]. Journal of Astronautics, 2011, 32(1): 224-231. DOI: 10.3873/j.issn.1000-1328.2011.01.035 |
| [7] |
李瑞雄, 陈务军, 付功义, 等. 透镜式缠绕肋压扁缠绕过程数值模拟及参数研究[J].
工程力学, 2011, 28(11): 244-250.
LI Ruixiong, CHEN Wujun, FU Gongyi, et al. Numerical simulation and parametric study on flattening and wrapping process of lenticular wrapped-rib[J]. Engineering Mechanics, 2011, 28(11): 244-250. |
| [8] |
李瑞雄, 陈务军, 付功义. 透镜式薄壁CFRP管空间伸展臂轴压屈曲分析及试验[J].
宇航学报, 2012, 33(8): 1164-1170.
LI Ruixiong, CHEN Wujun, FU Gongyi. Buckling analysis and experiment of lenticular cfrp thin-walled tube space boom under axial compression[J]. Journal of Astronautics, 2012, 33(8): 1164-1170. DOI: 10.3873/j.issn.1000-1328.2012.08.024 |
| [9] |
刘锦贤. 空间可展天线支撑结构热-结构分析[D]. 上海: 上海交通大学, 2013.
LIU Jinxian. Thermal-structural analysis for support structure of deployable space antenna[D]. Shanghai: Shanghai Jiao Tong University, 2013. |
| [10] |
陈务军.
空间可展结构体系与分析导论[M]. 北京: 中国宇航出版社, 2006: 1-50.
CHEN Wujun. Deployable space structures and analysis theory[M]. Beijing: China Astronautic Publishing House, 2006: 1-50. |
| [11] | WIE Bong. Thrust vector control of Solar sail spacecraft[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. San Francisco, California:AIAA, 2005: 15-18. DOI: 10.2514/6.2005-6086. |
| [12] | SICKINGER C, HERBECK L, BREITBACH E. Structural engineering on deployable CFRP booms for a solar propelled sailcraft[C]//Proceedings of the 54th International Astronautical Congress of the International Astronautical Federation, the International Academy of Astronautics, and the International Institute of Space Law. Bremen, Germany: AIAA, 2003.DOI: 10.2514/6.IAC-03-I.4.05. |
| [13] | WAWRZYNIAK G G, HOWELL K C. An adaptive, receding-horizon guidance strategy for solar sail trajectories[J]. The Journal of the Astronautical Sciences, 2012, 59(4): 650-675. DOI: 10.1007/s40295-014-0012-2 |
| [14] | JOHNSON L, WHORTON M, HEATON A, et al. NanoSail-D: a solar sail demonstration mission[J]. Acta Astronautica, 2011, 68(5/6): 571-575. DOI: 10.1016/j.actaastro.2010.02.008 |
| [15] | RIZVI F, LAWRENCE D. Solar sail attitude dynamics and coning control to attain desired orbital effects[C]//Proc. of ISSFD Symposium, Organized by Jet Propulsion Lab, NASA-caltech.[S.l.]: ISSFD, 2012. |
 2017, Vol. 49
2017, Vol. 49


