2. 航宇救生装备有限公司实验部,湖北 襄阳,441022
2. Dept. of Experiment, Aerospace Life-Support Equipment Co., Ltd., Xiangyang 441022, Hubei, China
翼伞是一种前缘有切口,利用冲压空气保持一定形状的柔性飞行器.翼伞由柔性不透气的材料包裹,通过肋片气孔平衡内部压力,增强飞行性能的稳定性,已广泛应用于飞行器回收、物资运输、港口消雾等领域[1-2].目前翼伞动力学模型中较少提及襟翼偏转的计算方法,为实现翼伞精确建模与自主归航,研究翼伞的气动性能有重要的意义.
翼伞气动性能研究早期使用风洞试验,美国国家航天局 (NASA) 与Notre Dame在1967-1968年进行了经典的风洞试验[3],研究展弦比、厚度、平面形状、弧度角等对翼伞气动性能的影响,由于风洞试验成本较高,目前更多的是数值模拟方向的研究.Mittal等[4-5]对二维翼伞在非定常流场下进行数值模拟,针对前缘切口的高度与倾斜度展开研究,讨论了前缘切口对翼伞气动性能的影响.然而二维翼伞的数值模拟忽略了翼伞环量展向椭圆分布与弧面下反角,与真实翼伞存在差距.Han等[6]分别建立了无气室与有气室的三维翼伞模型,结合数值模拟数据,分析气室对翼伞升阻力系数的影响,指出气室对平衡翼伞压力分布的重要性.Singh等[7]结合线性活塞理论,加入阵风干扰,研究三维翼伞对阵风的阶跃响应,并提出阵风减缓策略.Kalro等[8]对并行运算在翼伞数值模拟中的应用进行研究,提高数值模拟的效率.Cao等[9]针对前缘开口翼伞在定常环境下进行数值模拟,主要研究翼型、前缘切口、弧面下反角等因素对翼伞气动性能的影响.Potvin等[10]则考虑大展弦比翼伞伞衣膨胀形成的“鼓包”,在不同迎角下对翼伞气动性能进行数值模拟,而小展弦比翼伞的伞衣膨胀效果相对不明显,可以忽略其影响.上述研究主要集中在滑翔阶段翼伞气动性能的数值模拟,而对转向与雀降阶段中襟翼偏转影响的研究相对缺乏.传统翼伞的气动模型将襟翼偏转通过增大迎角近似模拟[11],与实际情况存在较大误差.
本文基于上述研究成果,重点研究襟翼偏转对翼伞气动性能的影响,首先引入基于CFD的襟翼偏转气动计算方法,将襟翼偏转下的翼伞气动模型的修正问题转为参数辨识问题;然后针对转向与雀降对应的不同襟翼偏转方式进行CFD数值模拟,研究翼伞气动性能的变化,并通过NASA风洞试验验证数值模拟的有效性;最后通过最小二乘法结合气动模拟数据进行参数辨识,完成翼伞气动模型的修正工作.
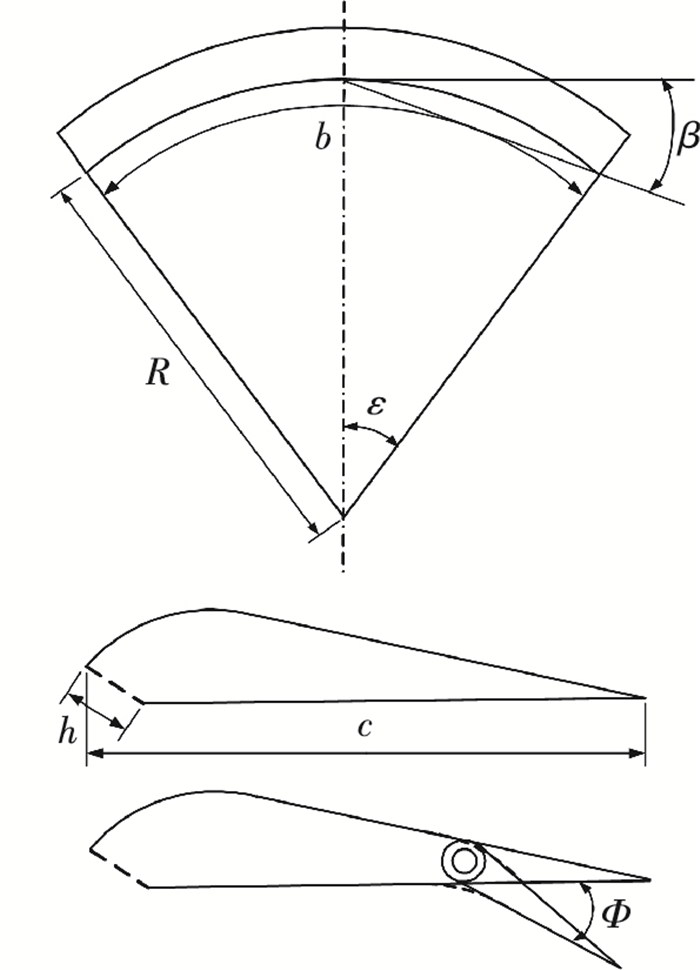
1 襟翼偏转翼伞气动模型 1.1 翼伞气动外形翼伞的气动外形如图 1所示,其中气动弦长c为2.133 6 m,展长b为6.400 8 m,弧面下反角β为9.55°,伞绳R为9.601 2 m,前缘切口高度h为0.242 1 m.并对翼伞做如下简化:1) 翼伞近似刚体,仅在襟翼偏转时考虑形变;2) 伞衣结构不透气;3) 忽略伞绳及负载.在保证数值模拟精度的前提下,上述简化可以降低计算成本,缩短数值模拟周期.
|
图 1 翼伞气动外形参数 Figure 1 Aerodynamic shape parameters of parafoil |
传统翼伞模型进行气动计算时,将伞衣沿展向对称等长分为8片,每片升力系数从外到里乘以0.60、1.00、1.16、1.24作为修正因子[12],对应气动方程为:
| $ {\mathit{\boldsymbol{F}}_{{\rm{aero}}}} = \sum\limits_{i = 1}^8 {\mathit{\boldsymbol{T}}{\mathit{\boldsymbol{R}}_{i - o}}\left( {{\mathit{\boldsymbol{F}}_{{\rm{L}},i}} + {\mathit{\boldsymbol{F}}_{{\rm{D}},i}}} \right)} , $ |
| $ {\mathit{\boldsymbol{M}}_{{\rm{aero}}}} = \sum\limits_{i = 1}^8 {{\mathit{\boldsymbol{L}}_{o - i}}\mathit{\boldsymbol{T}}{\mathit{\boldsymbol{R}}_{i - o}}\left( {{\mathit{\boldsymbol{F}}_{{\rm{L}},i}} + {\mathit{\boldsymbol{F}}_{{\rm{D}},i}}} \right)} , $ |
| $ {\mathit{\boldsymbol{L}}_{o - i}} = \left[ {\begin{array}{*{20}{c}} 0 & { - z} & y\\ z & 0 & { - x}\\ { - y} & x & 0 \end{array}} \right], $ |
| $ \mathit{\boldsymbol{T}}{\mathit{\boldsymbol{R}}_{i - o}} = \left[ {\begin{array}{*{20}{c}} 1 & 0 & 0\\ 0 & {\cos {\gamma _i}} & {\sin {\gamma _i}}\\ 0 & { - \sin {\gamma _i}} & {\cos {\gamma _i}} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{F}}_{{\rm{L}},i}} = 0.5{k_i}{C_1}\rho S\sqrt {v_{xi}^2 + v_{yi}^2 + v_{zi}^2} \left[ {\begin{array}{*{20}{c}} {{v_{yi}}}\\ {{v_{xi}}}\\ 0 \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{F}}_{{\rm{D}},i}} = - 0.5{C_{\rm{D}}}\rho S\sqrt {v_{xi}^2 + v_{yi}^2 + v_{zi}^2} \left[ {\begin{array}{*{20}{c}} {{v_{xi}}}\\ {{v_{yi}}}\\ {{v_{zi}}} \end{array}} \right]. $ |
式中:i=1, 2, …, 8;Faero、Maero分别为翼伞气动力与气动力矩;Lo-i为翼伞质心到各分片i质心的矢量;TRi-o为分片i坐标系到翼伞坐标系的转换矩阵,矩阵中的γi为分片i转换角;FL, i、FD, i分别为分片i的升力与阻力;CL、CD分别为升、阻力系数;ρ为空气密度;S为翼伞特征面积;v为伞体坐标系下气流速度.
翼伞气动模型难点在于气动系数CL, CD的确定,传统计算方法为:
| $ \begin{array}{*{20}{c}} {{C_{\rm{L}}} = {C_{{{\rm{L}}_0}}} + \frac{{2{\pi ^2}fA\left( {1 + 0.8\bar c} \right)}}{{\pi A + 2\pi f\left( {1 + \in } \right)\left( {1 + 0.8\bar c} \right)}}\alpha ,}\\ {{C_{\rm{D}}} = {C_{{{\rm{D}}_0}}} + \frac{{C_{\rm{L}}^2\left( {1 + \sigma } \right)}}{{\pi A}}.} \end{array} $ |
式中:CL0、CD0分别为零迎角升、阻力系数;A为展弦比;σ、∈分别为翼型影响因子;f=(πA/a0) tanh (a0/πA) 为展弦比影响因子;c为翼伞相对厚度.
上述计算方式存在较大缺陷,未考虑襟翼偏转带来的附加气动力.襟翼偏转δ仅通过增大迎角α近似模拟,忽略了伞衣形变影响,造成传统气动计算存在较大误差.为提高翼伞的气动计算精度,考虑襟翼偏转的附加气动力,本文对传统气动模型进行修正,如:
| $ \begin{array}{l} {C_{\rm{L}}} = {C_{{{\rm{L}}_0}}} + {C_{{\rm{L}}\alpha }}\alpha + {C_{{\rm{L}}\delta e}}{\delta _e} + {C_{{\rm{L}}\delta a}}{\delta _a},\\ {C_{\rm{D}}} = {C_{{{\rm{D}}_0}}} + {C_{{\rm{D}}\alpha }}\alpha + {C_{{\rm{D}}\delta e}}{\delta _e} + {C_{{\rm{D}}\delta a}}{\delta _a}. \end{array} $ |
式中:CL0为初始升力系数;CLα为升力系数斜率;CD0为初始阻力系数;CDα为阻力系数斜率;δe= δL-δR为左、右侧襟翼偏转差值;δa=min {δL, δR}为左、右侧襟翼偏转较小值;CLδe、CLδa、CDδe、CDδa分别为偏转系数.
针对偏转系数与迎角之间的非线性关系,使用二阶模型即可满足:
| $ \begin{array}{l} {C_{{\rm{L}}\delta e}} = {C_{{\rm{L}}\delta {e_0}}} + {C_{{\rm{L}}\delta e\alpha }}\alpha + {C_{{\rm{L}}\delta e{\alpha ^2}}}{\alpha ^2},\\ {C_{{\rm{L}}\delta a}} = {C_{{\rm{L}}\delta {a_0}}} + {C_{{\rm{L}}\delta a\alpha }}\alpha + {C_{{\rm{L}}\delta a{\alpha ^2}}}{\alpha ^2},\\ {C_{{\rm{D}}\delta e}} = {C_{{\rm{D}}\delta {e_0}}} + {C_{{\rm{D}}\delta e\alpha }}\alpha + {C_{{\rm{D}}\delta e{\alpha ^2}}}{\alpha ^2},\\ {C_{{\rm{D}}\delta a}} = {C_{{\rm{D}}\delta {a_0}}} + {C_{{\rm{D}}\delta a\alpha }}\alpha + {C_{{\rm{D}}\delta a{\alpha ^2}}}{\alpha ^2}. \end{array} $ |
至此翼伞模型中的襟翼偏转气动计算问题,转为对12个偏转系数因子的辨识问题,本文通过CFD数值模拟结合最小二乘法对其进行辨识.
2 CFD求解方法与分析 2.1 CFD模型与网格划分共使用5个不同形态的翼伞CFD模型,如图 2所示.模型1中襟翼无偏转,模型2中襟翼双侧1/3偏转,模型3中襟翼双侧2/3偏转,模型4中襟翼双侧全偏转,模型5中襟翼单侧2/3偏转.其中模型1、2、3、4用于雀降阶段,模型1、3、5用于转向阶段.

|
图 2 翼伞CFD模型 Figure 2 CFD models of parafoil |
翼伞以弦长75%处为轴弯折[3],即后缘25%的翼尖向下弯折,弯折角度称为下折角.1/3偏转对应下折角为25°,2/3偏转对应下折角为50°,全偏转对应下折角为75°,展向两侧偏转量大,展向中部偏转量小.
采用三维非结构化化网格进行空间划分,如图 3所示,流场边界条件应尽量远离扰动源 (翼伞),但实际计算不允许边界条件取得过远,根据计算经验确定边界距离翼伞分别为10c, 5c, 10c,c为翼伞的气动弦长.翼伞近壁面网格需要加密,网格法向拉伸率不宜过大[13],控制在1.12以内,网格总数大致为150万.

|
图 3 流场空间网格划分 Figure 3 Mesh densities of flow field |
流场环境设置如下:流体为不可压空气,流速为12.192 m/s,入口为速度入口,出口为压力出口,非进出口为自由边界,翼伞为壁面边界.翼伞气流迎角设置范围为0°~18°,每隔2°模拟1次,1种模型需要模拟10组数据,全部数据共70组.每次模拟时间大致为120 min,在失速迎角附近需要大致180 min.
使用的控制方程为三维笛卡尔坐标系下的时均Navier-Stokes (RANS) 方程[14],其张量指标形式表示为:
| $ \begin{array}{*{20}{c}} {\frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}} \right) = 0,}\\ {\frac{\partial }{{\partial t}}\left( {\rho {u_i}} \right) + \frac{\partial }{{\partial {x_j}}}\left( {\rho {u_i}{u_j}} \right) = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left( {\mu \frac{{\partial {u_i}}}{{\partial {x_j}}} - \rho \overline {{{u'}_i}{{u'}_j}} } \right) + {S_i}.}\\ {\left( {i.j = 1,2,3} \right)} \end{array} $ |
式中:i, j取值范围为 (1, 2, 3),表示三维笛卡尔坐标系的3个方向; u为流体速度;u′为流体脉冲速度;ρ为流体密度;p为流体动能;μ为扩散系数;S为源项.
空间离散方式为二阶迎风格式,求解器选择基于分离式求解算法的SIMPLE求解器.湍流模型选择RNG k-ε二方程模型[15],对近壁面逆压梯度变化有较好捕捉效果.
2.3 CFD有效性验证使用文献[3]中风洞试验数据对CFD的有效性进行验证.试验使用的ND模型为伞绳刚性连接,NASA模型为伞绳柔性连接.
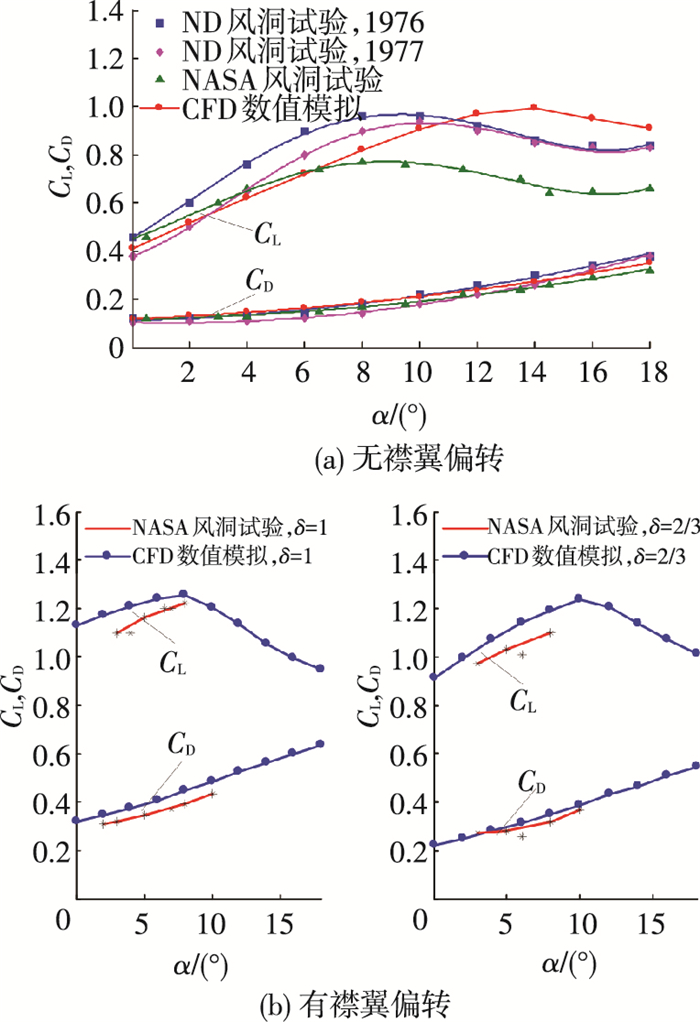
翼伞滑翔阶段,不存在襟翼偏转,伞衣未发生形变.如图 4(a)所示,升力系数与风洞试验数据接近,失速迎角偏大,是风洞试验翼伞上翼面气流提前分离造成的,这些偏差在翼伞数值模拟中普遍存在,不影响翼伞建模.阻力系数与风洞试验数据重合较好.翼伞雀降阶段,存在襟翼偏转,伞衣发生形变.如图 4(b)所示,襟翼2/3偏转与完全偏转情况下,升阻力系数与风洞试验数据相对接近,偏差存在是风洞试验伞衣厚度、粗糙度、弹性形变等因素造成的.在数值模拟过程中这些偏差的存在是合理的,从而验证了CFD数值模拟的有效性.
|
图 4 风洞试验与数值模拟对比 Figure 4 Comparison of wind tunnel test and numerical simulation |
翼伞雀降阶段,襟翼双侧偏转,增大阻力实现减速.由于翼伞为柔性材料,襟翼偏转带来翼伞伞衣形变,对应气动性能发生改变.
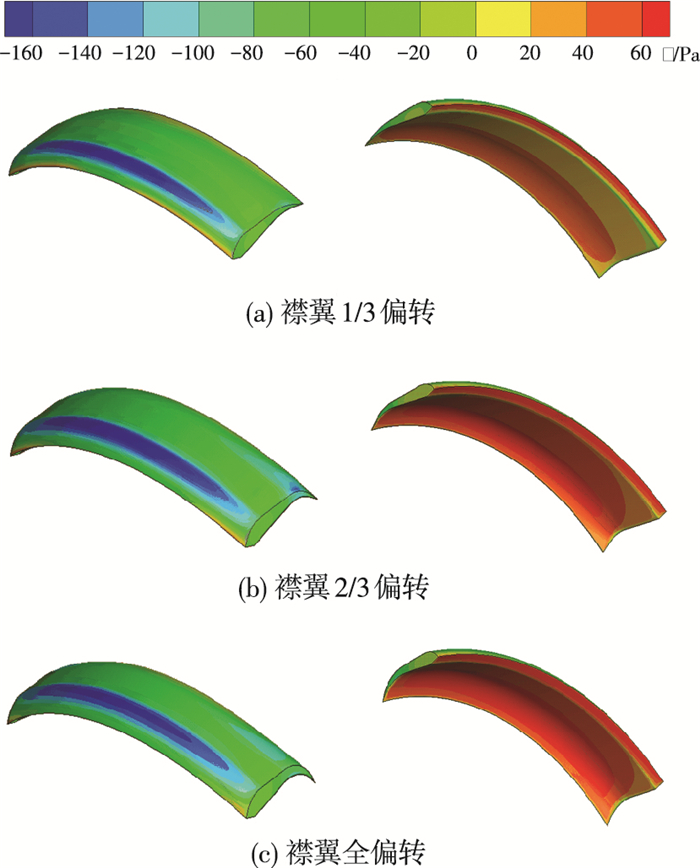
CFD模型选择模型2、3、4.如图 5所示,压力对称分布,随着襟翼偏转量的增加,低压区范围缓慢增加.展向中部低压区明显,在下折角附近没有新的低压区产生,而展向边缘低压区不明显,在下折角附近有新的低压区产生.相对而言,高压区范围迅速增加,展向中部高压范围大于展向边缘,集中在前缘开口与下折角部分,是阻力的主要来源.
|
图 5 双侧襟翼偏转下翼伞压力分布 Figure 5 Pressure distribution of parafoil with bilateral flap deflection |
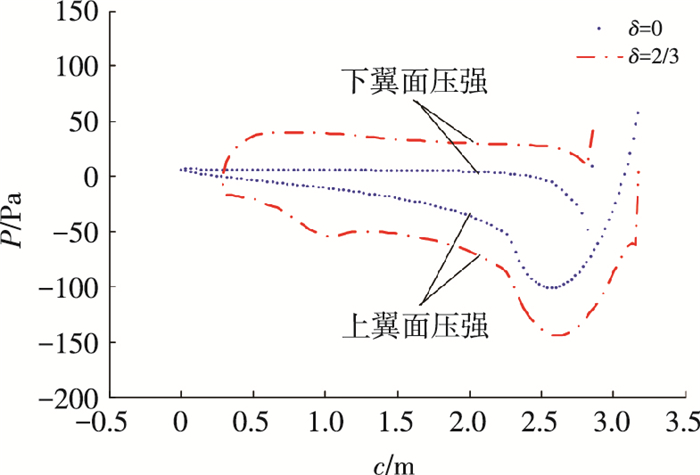
如图 6所示,伞衣表面最低压均出现在上翼面圆弧过渡区域,最高压均出现在前缘切口区域.襟翼双侧无偏转时,翼伞上翼面与下翼面的弦向压力分布,与气动外形即为相似,压力差与伞衣厚度相关,压力最小值为-101.2 Pa,最大值为59.7 Pa.襟翼双侧2/3偏转时,翼伞上翼面与下翼面压力分布,与气动外形存在较大差异,压力差相比之下有明显增加,压力最小值为-145.3 Pa,最大值为48.6 Pa.
|
图 6 翼伞弦向压力分布对比 Figure 6 Comparison of parafoil chordwise pressure distribution |
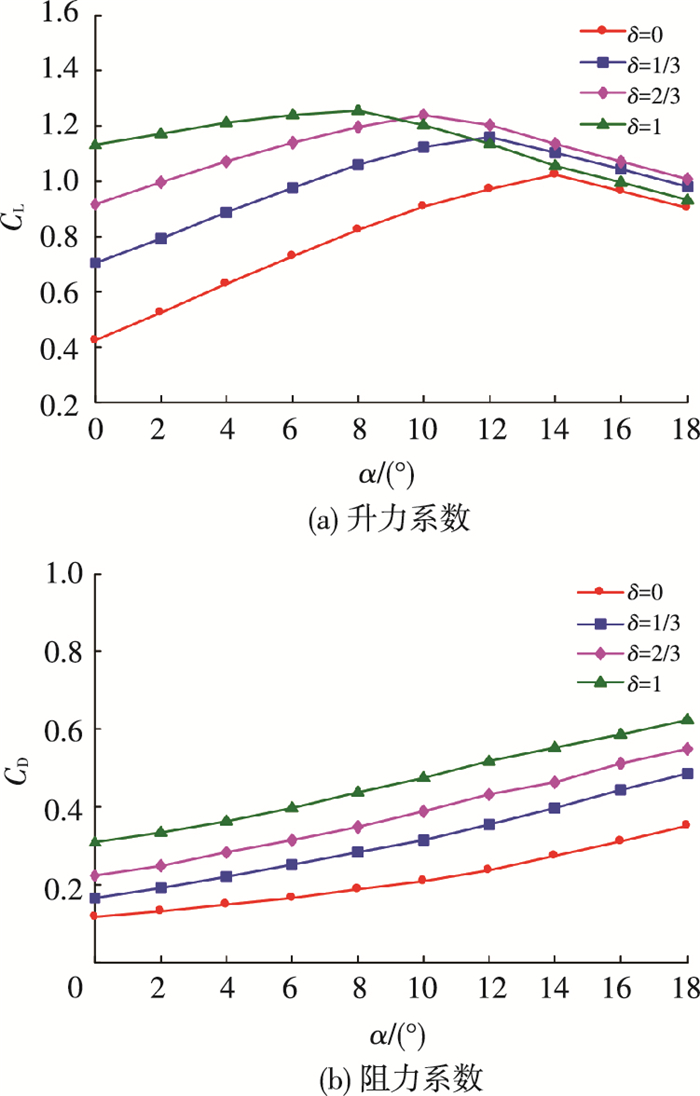
对不同襟翼偏转量分别数值模拟,如图 7所示,随着偏转量的增加,翼伞失速迎角逐渐减小,分别为14°、12°、10°、8°.相同迎角的升力系数迅速增大,增长速度由快变慢甚至由正变负;相同迎角的阻力系数呈单调递增,增长速度相对平稳.因此,襟翼偏转对翼伞气动性能存在非线性影响,进行偏转参数因子的辨识是必要的.
|
图 7 双侧襟翼偏转翼伞气动系数 Figure 7 erodynamic coefficience of parafoil with bilateral flap deflection |
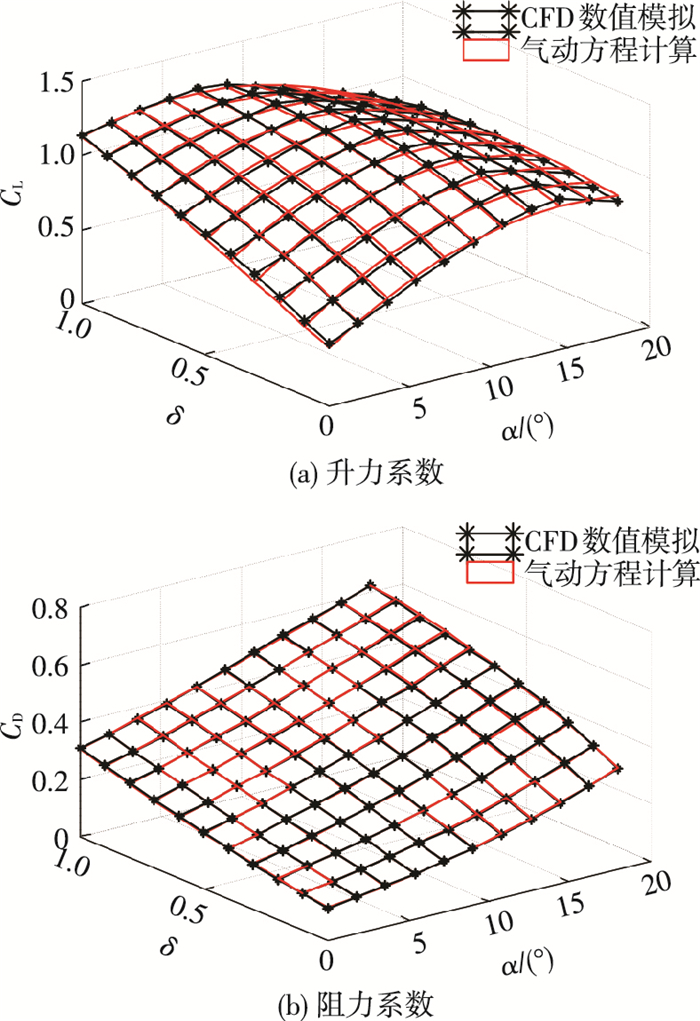
通过最小二乘法进行参数辨识,可得到表 1中修正因子的数值.如图 8所示,通过修正气动系数的计算值与CFD数据重合很好,最大偏差与CFD数值相差5.47%,位置在无偏转时失速迎角附近.不同的襟翼偏转量对应不同的升阻力系数曲线,比传统不考虑襟翼偏转的翼伞气动方程更客观科学,为翼伞雀降阶段建模提供参考.
| 表 1 双侧襟翼偏转翼伞模型修正 Table 1 Modification of parafoil model with bilateral flap deflection |
|
图 8 双侧襟翼偏转气翼伞动系数曲面 Figure 8 Aerodynamic coefficient surface of parafoil with bilateral flap deflection |
翼伞转向阶段,襟翼单侧偏转,使翼伞向偏转一侧转向,偏转量越大,转弯半径越小.由于压力不对称,翼伞展向环量不再满足椭圆分布,传统翼伞气动方程同样不适用.
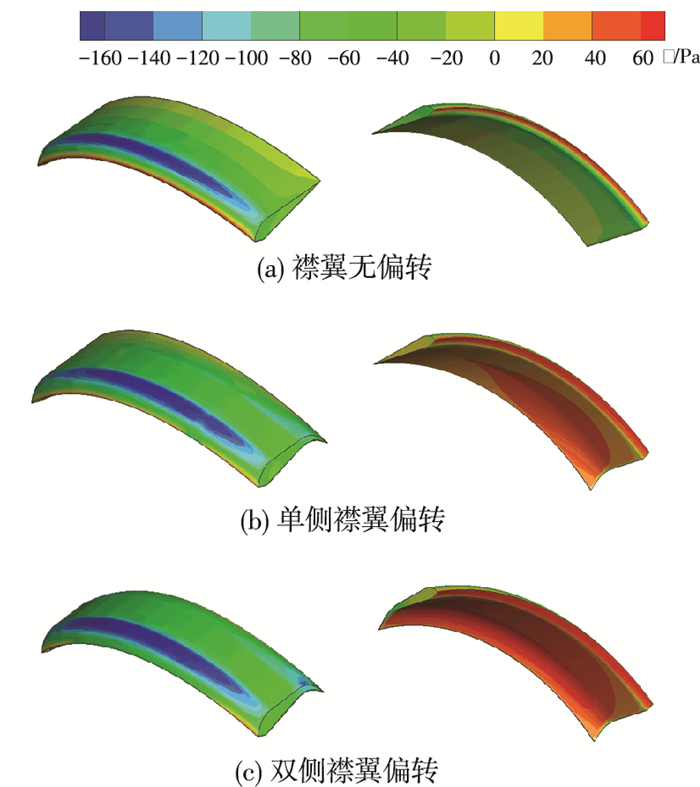
CFD模型选择模型1、3、5.如图 9所示,单侧偏转时上翼面低压区范围介于无偏转低压区与双侧偏转低压区之间,均集中在圆弧过渡区域.相对而言,下翼面高压区分布形状存在不规则性,并且向偏转侧偏移,是翼伞下翼面两侧的迎风面积不同造成的,同时也是翼伞偏航力矩的主要来源.
|
图 9 单、双侧襟翼偏转翼伞压力分布对比 Figure 9 Comparison of pressure distribution of parafoil with unilateral and bilateral flap deflection |
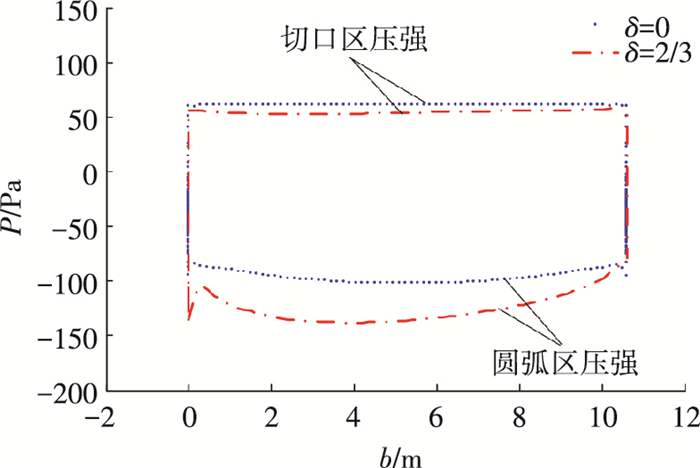
如图 10所示,襟翼单侧无偏转时,伞衣表面压力沿展向对称分布,压力最小值为-101.2 Pa,集中在上翼面展向中部的圆弧区域,压力最大值为59.7 Pa,集中在展向中部前缘切口区域.襟翼单侧2/3偏转时,伞衣表面压力沿展向非对称分布,压力最小值为-145.3 Pa,集中在上翼面展向偏转侧的圆弧区域,压力最大值为58.8 Pa,集中在展向两侧前缘切口区域.对于展向边缘的低压突峰,是由上翼面新低压区造成的.
|
图 10 翼伞展向压力分布对比 Figure 10 Comparison of parafoil spanwise pressure distribution |
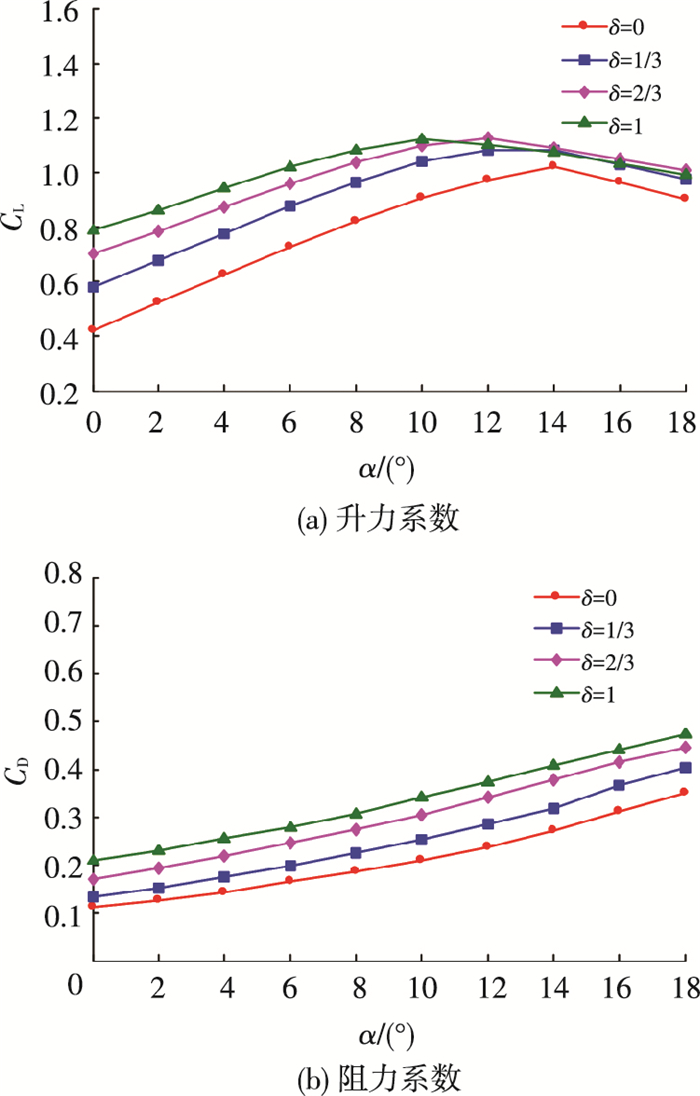
对不同襟翼偏转量分别数值模拟,如图 11所示,随着偏转量的增加,翼伞失速迎角逐渐减小,分别为14°、13°、12°、10°.相同迎角的升力系数迅速增大,增长速度由快变慢甚至由正变负;相同迎角的阻力系数呈单调递增,增长速度相对平稳.与雀降情况相似,襟翼偏转对翼伞气动性能同样存在非线性影响.
|
图 11 单侧不同偏转量气动系数变化 Figure 11 Aerodynamic coefficience of parafoil with unilateral flap deflection |
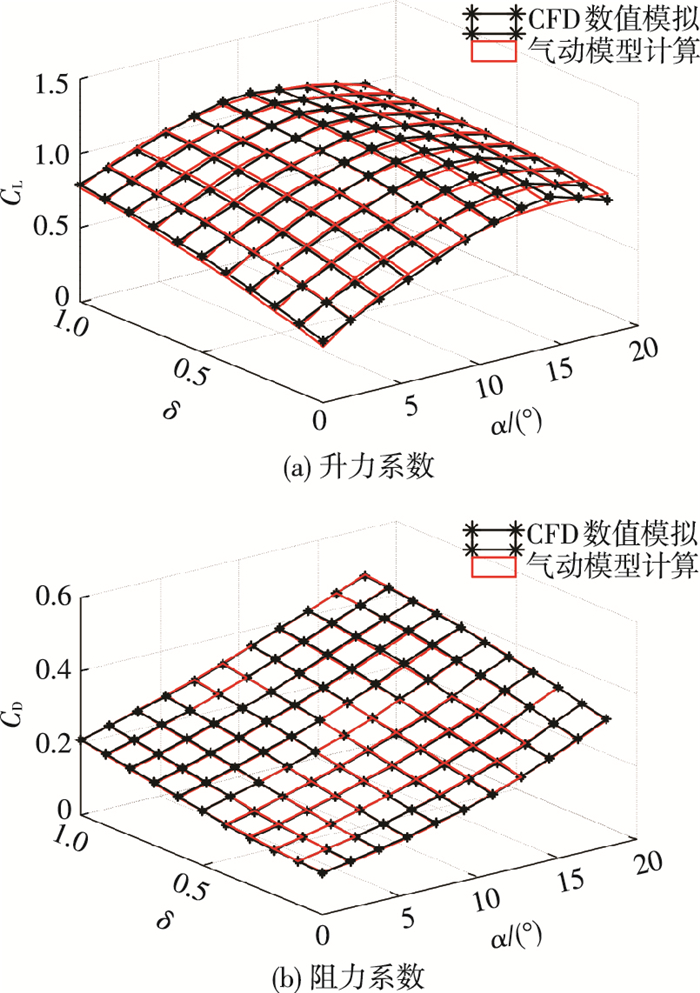
通过最小二乘法进行参数辨识,可得到表 2中修正因子的数值.如图 12所示,修正气动系数计算值与CFD数据重合很好,最大偏差与CFD数值相差4.93%,位置在无偏转时失速迎角附近.不同的襟翼偏转量对应不同的升阻力系数曲线,比传统不考虑襟翼偏转的翼伞模型更客观科学,为翼伞转弯阶段建模提供参考.
| 表 2 单侧襟翼偏转翼伞模型修正 Table 2 Modification of parafoil model with unilateral flap deflection |
|
图 12 单侧襟翼偏转气动系数曲面 Figure 12 Aerodynamic coefficient surface of parafoil with unilateral flap deflection |
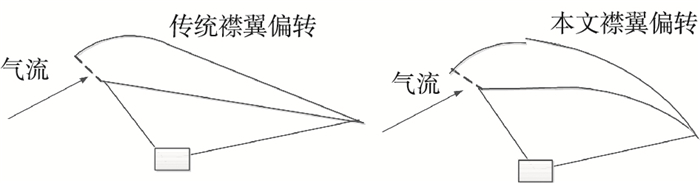
传统模型无论翼伞处于滑翔、转向、雀降阶段,均通过增大迎角模拟襟翼偏转,如图 13所示,由于为考虑襟翼偏转带来的伞衣形变,其准确性必然下降.表 3数据表明,双侧襟翼无偏转,传统模型与修正模型气动系数差别可忽略不计;双侧襟翼完全偏转,传统模型通过增大迎角模拟,修正模型通过设置偏转量模拟,传统模型升力系数偏大17.3%,阻力系数偏小18.5%.传统模型计算误差随着襟翼偏转量的增加而增加,影响翼伞模型精度.通过CFD与最小二乘法得到的修正模型,对翼伞精确建模存在重要意义.
|
图 13 翼伞襟翼偏转对比 Figure 13 Comparison of parafoil flap deflection |
| 表 3 传统模型与修正模型气动系数对比 Table 3 Comparison of aerodynamic coffiences of traditional and modified model |
1) 襟翼偏转引起翼伞气动性能急剧变化,随着偏转量的增加,翼伞压强分布改变,失速迎角减小,气动系数激增,相比无偏转阶段存在很大差异.
2) 结合CFD数值模拟与最小二乘法,完成翼伞气动模型的修正工作.对比模拟数据,修正后模型较好描述了翼伞气动性能与襟翼偏转的变化规律.
3) 针对传统气动模型在翼伞转向与雀降阶段存在的升力系数偏高、阻力系数偏低的问题,修正后气动模型的计算精度得到较大提高,为翼伞的精确建模提供参考.
| [1] | TAO Jin, SUN Qinglin, ZHU Erlin, et al. Quantum genetic algorithm based homing trajectory planning of parafoil system[C]//Proceedings of the 34th Chinese Control Conference, CCC 2015. Hangzhou, China: IEEE, 2015: 2523-2528.DOI:DOI:10.1109/ChiCC.2015.7260028. |
| [2] | ZHU Erlin, SUN Qinglin, TAN Panlong, et al. Modeling of powered parafoil based on Kirchhoff motion equation[J]. Nonlinear Dynamics, 2015, 79(1): 617-629. DOI: 10.1007/s11071-014-1690-9 |
| [3] | NICOLAIDES J D. Parafoil wind tunnel tests[R]. Indiana: University of Notre Dame, 1971. |
| [4] | BALAJI R, MITTAL S, RAI A K. Effect of leading edge cut on the aerodynamics of ram-air parachutes[J]. International Journal for Numerical Methods in Fluids, 2005, 47(1): 1-17. DOI: 10.1002/fld.779 |
| [5] | MITTAL S, SAXENA P, SINGH A. Computation of two-dimensional flows past ram-air parachutes[J]. International Journal for Numerical Methods in Fluids, 2001, 35(6): 643-667. DOI: 10.1002/1097-0363(20010330)35:6 |
| [6] | HAN Yihua, YANG Congxin, WANG Yuwei, et al. Aerodynamics simulation of a large multi-cells parafoil[C]// Proceedings of the 20th AIAA Aerodynamic Decelerator Systems Technology Conference. Seattle, WA: AIAA, 2009: 2978-2991. |
| [7] | SINGH R, BAEDER J D. Direct calculation of three-dimensional indicial lift response using computational fluid dynamics[J]. Journal of Aircraft, 1997, 34(4): 465-471. DOI: 10.2514/2.2214 |
| [8] | KALRO V, TEZDUYAR T. A parallel 3D computational method for fluid-structure interactions in parachute systems[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 190(3/4): 321-332. DOI: 10.1016/S0045-7825(00)00204-8 |
| [9] | CAO Yihua, ZHU Xu. Effects of characteristic geometric parameters on parafoil lift and drag[J]. Aircraft Engineering & Aerospace Technology, 2013, 85(4): 280-292. DOI: 10.1108/AEAT-Jun-2011-0096 |
| [10] | POTVIN J, HURST B, PEEK G. Semi-numerical derivation of the opening shock factor and inflation time for slider-reefed parafoils[C]//Proceedings of the 19th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar. Williamburg, VA: AIAA, 2007: 2508-2517.DOI: 10.2514/6.2007-2508. |
| [11] | LINGARD J. The aerodynamics of gliding parachutes[C]// Proceedings of the 9th Aerodynamic Decelerator and Balloon Technology Conference. Albuquerque, NM: AIAA, 1986: 1-13.DOI: 10.2514/6.1986-2427. |
| [12] |
熊菁. 翼伞系统动力学与归航方案研究[D]. 长沙: 国防科学技术大学, 2005.
XIONG Jing. Research on the dynamics and homing project of parafoil system[D]. Changsha: National University of Defense Technology, 2005. |
| [13] | ONATE E, VALLS A, GARCÍA J. Computation of turbulent flows using a finite calculus-finite element formulation[J]. International Journal for Numerical Methods in Fluids, 2007, 54. DOI: 10.1002/fld.1476 |
| [14] |
王福军.
计算流体动力学分析: CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004: 115-116.
WANG Fujun. Computational fluid dynamics analysis: principles and applications of CFD software[M]. Beijing: Tsinghua University Press, 2004: 115-116. |
| [15] | MANSOUR N, KIM J, MOIN P. Near wall k-epsilon turbulence modeling[J]. AIAA Journal, 1989, 27(8): 1068-1073. DOI: 10.2514/3.10222 |
 2017, Vol. 49
2017, Vol. 49


