随着卫星技术的发展，由多颗星组成的星座系统在多个领域都得到了重要的应用^[1-2].不论是遥感卫星对地成像，还是通信卫星与地面站进行数据交换都涉及到卫星对地覆盖分析.并且大多数的星座优化设计和分析都是基于卫星对地球表面的可视性计算实现的^[3].

目前，卫星星座对地覆盖问题最常用的方法是网格点法.Morrison^[4]在1973年就提出将区域按照某种规则划分为若干个网格，用卫星对网格点的覆盖能力来表示卫星对整个网格区域的覆盖能力.文献[5]在分析星座对地覆盖性能时，也是将目标区域进行均匀网格划分，计算星座在任意时刻对目标区域的覆盖情况.文献[6]通过将空间球面圆进行网格划分，分析了低轨凝视传感器的空间球面覆盖性能，文献[7]分别在近空间平台对地区域覆盖优化设计和考虑多项卫星配置参数下通信卫星星座设计中，将地球表面进行网格划分，分析航天器覆盖性能.文献[8]采用网格点抽样的方法进行覆盖率计算，并从理论上推导了网格点法划分大小和计算误差之间的关系.但是，通过将目标区域划分为足够多的点进行星座对地覆盖计算与覆盖性能分析，主要缺点是计算效率低，且不能保证计算结果的可靠性.

文献[9]通过对星座空间几何构形进行划分，研究了全球连续性完全覆盖下的Rosette星座优化设计方法.文献[10]采用改进网格点法进行星座对地面目标覆盖性能计算，研究了通用航空飞行器组网星座的优化设计.文献[11]提出一种半长轴分析方法进行全球连续性覆盖周期性轨道设计，该算法通过绘制卫星每次经过不同纬线圈时的升交点和降交点，然后进行统计排序，从而判断是否存在缝隙.这几种方法在计算效率上都有所提高，但只局限于对全球目标的完全覆盖分析.文献[12]通过定义覆盖状态函数和覆盖区域函数，分析了星座对区域的完全覆盖问题和连续性覆盖问题，提出了卫星在固定时刻对纬线的覆盖范围计算方法，消除了抽样对覆盖结果的可信度影响，但该方法同样要基于经度条带的划分精度.

根据卫星对地覆盖几何特性，基于球面Delaunay三角网络和Voronoi图的性质以及快速构建方法，本文定义了卫星的所属覆盖区域，并对该区域做了定性与定量描述，从而将多星覆盖问题转换为单星覆盖问题，旨在提出满足覆盖约束下，星座对任意类型地面目标区域的确定性计算方法，从而精确、快速地计算星座对目标区域的覆盖能力.

1 星座对目标区域覆盖能力分析 1.1 卫星对地覆盖几何特性

已知地球半径为R_e，卫星轨道高度为h，受地面目标最小观测仰角γ_min的约束，卫星对地的最大覆盖半幅宽为^[13]

$ d={{\cos }^{-1}}\left( \frac{{{R}_{\text{e}}}\cdot \cos \left( {{\gamma }_{\min }} \right)}{{{R}_{\text{e}}}+h} \right)-{{\gamma }_{\min }}. $

同时，对于一个由轨道高度相同的圆轨道卫星构成的星座，已知A, B, C是该星座中任意3颗星的星下点，要保证球面ΔABC内任意一点都能被覆盖，只需要确保ΔABC内距离3个顶点最远的点P被覆盖.可见，将1个由N颗星构成的星座，在任意状态下的空间几何构形剖分成若干个相邻且互不相交的球面三角形.计算三角网中所有球面三角形内最远点P到顶点的半径r_i，如果满足^[10]:

$ d\ge \max \left\{ {{r}_{i}} \right\},\left( i=1,2,\cdots ,n \right). $

则卫星星座在当前状态下可以实现一重全球完全覆盖，若在整个星座重构周期内的任意时刻该条件都成立，则表明该卫星星座能够实现一重连续性全球完全覆盖.

1.2 星座对地覆盖分析

定义1    卫星的邻接结点.球面三角网剖分结果中，将包含卫星星下点的球面三角形的外接圆圆心记作该卫星的邻接结点.

定义2    卫星的邻接多边形.以卫星星下点为中心，依次顺序连接该点的所有邻接结点围成的多边形区域.

定义3    卫星所属覆盖区域.卫星的邻接多边形区域和目标覆盖区域的相交区域.

已知卫星星座C={S₁, S₂, …, S_N}，通过对某一时刻星座在地球表面上投影点的空间几何构形进行球面Delaunay三角网剖分和Voronoi图划分，其性质决定了当前时刻星座中如果存在1颗卫星S_i不能实现对其所属覆盖区域的完全覆盖，则对于任意的S_j都不能对S_i的所属覆盖区域的漏缝进行覆盖，即该状态下，星座必然不能实现对目标区域的完全覆盖.因此，要实现对目标区域的完全覆盖，则整个星座中所有卫星均能实现对其所属覆盖区域的完全覆盖.

2 卫星对其所属覆盖区域的覆盖计算

由上述分析可见，星座对地覆盖问题可以转换为多个独立的单星对其所属覆盖区域的覆盖问题，并且生成的卫星所属覆盖区域是球面大圆弧段和小圆弧段围城的多边形区域，因此，卫星对其所属覆盖区域的覆盖计算，就可以归结为卫星实际覆盖圆与其所属覆盖区域的相交性的分析和两球面圆的相交区域计算.

对于一个由多个球面大圆弧段和小圆弧段围成的球面区域Ω，将区域的边界记为∂Ω，区域的内部记为Ω^-，区域的外部记为Ω⁺.区域边界∂Ω的顶点集合为V={v₁, v₂, …, v_n}，区域边界∂Ω上的所有弧段集合为$E = \left\{ {\mathop {{v_1}{v_2}}\limits^\frown ,\mathop {{v_2}{v_3}}\limits^\frown , \cdots ,\mathop {{v_n}{v_1}}\limits^\frown } \right\}$，所对应的弧段的圆心和半径集合分别为{o₁₂, o₂₃, …, o_n1}和{r₁₂, r₂₃, …, r_n1}.将球面上的任意一点p到弧段$\mathop {{v_i}{v_j}}\limits^\frown $所在球面圆的圆心o_ij的球面距离记作dis (p, o_ij).如果$\forall \mathop {{v_i}{v_j}}\limits^\frown $，dis (p, o_ij)≤r_ij成立，则p∈Ω^-；如果$\exists \mathop {{v_i}{v_j}}\limits^\frown $，dis (p, o_ij) > r_ij成立，则p∈Ω⁺.

2.1 卫星对其所属覆盖区域的覆盖能力计算

对于地球表面上的一点p，以p点为圆心，α为半径画圆，E, F是圆上任意两点.θ₁、θ₂分别为点E和点F相对于圆心p的方向角，则球面扇形$p\mathop {EF}\limits^\frown $的有向面积为

$ {{S}_{p\overset\frown{EF}}}=\left( {{\theta }_{2}}-{{\theta }_{1}} \right)\cdot R_{\text{e}}^{2}\cdot \left( 1-\cos \alpha \right). $

已知球面上的两点O₁, O₂，其球面距离为d，以O₁点为圆心，α为半径画圆，记作Θ₁，以O₂点为圆心，r为半径画圆，记作Θ₂，圆Θ₁和Θ₂相较于p₁, p₂两点，将由点O₂和弧段p₁p₂围成的区域记作R，区域的面积记作S_R.

如果d < α且α-d < r < α+d，即O₂点在圆Θ₁内部，如图 1所示，区域R如图 1中阴影部分所示.则

$ {{S}_{R}}={{S}_{{{O}_{1}}\overset\frown{{{p}_{1}}{{p}_{2}}}}}-{{S}_{O1O2{{p}_{1}}}}-{{S}_{O1O2{{p}_{2}}}}. $

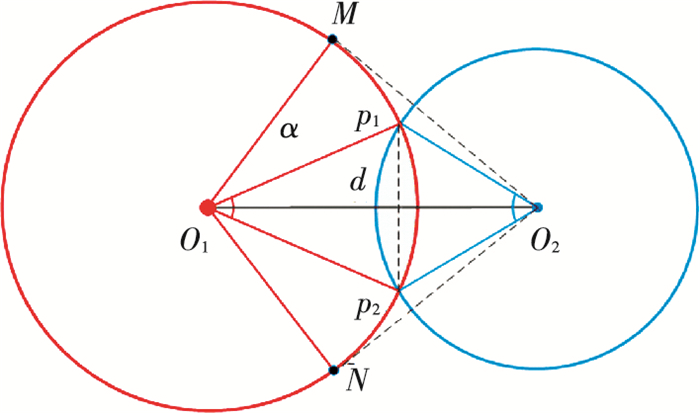
如果d≥α，即O₂点在圆Θ₁外部.此时，当两圆相交且满足cos d=cos α·cos r，则可得到两个球面直角三角形O₁MO₂和O₁NO₂，其中，M, N为两圆的交点.

当d-α < r < acos (cos d/cos α)，如图 2所示，区域R如图 2中阴影部分所示，则

$ {{S}_{R}}={{S}_{{{O}_{2}}\overset\frown{{{p}_{1}}{{p}_{2}}}}}-\left( {{S}_{{{O}_{2}}{{p}_{1}}{{p}_{2}}}}+{{S}_{{{O}_{1}}{{p}_{2}}{{p}_{1}}}}-{{S}_{{{O}_{1}}\overset\frown{{{p}_{2}}{{p}_{1}}}}} \right). $

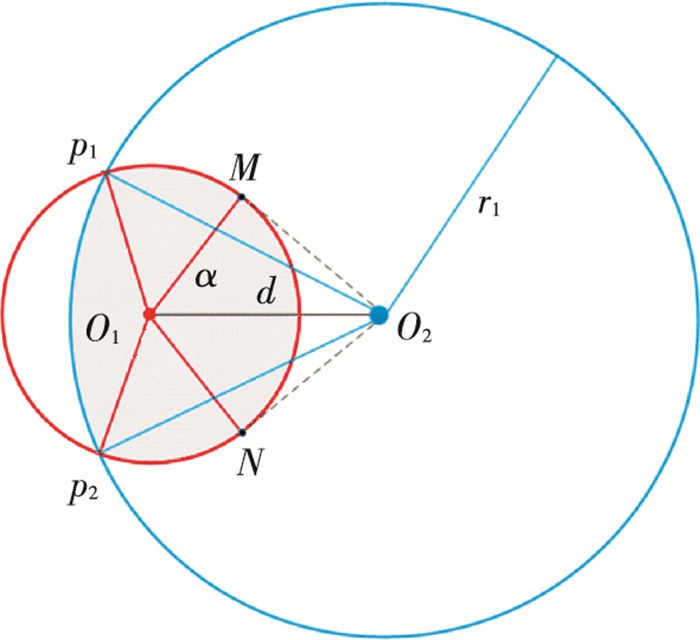
当acos (cos d/cos α)≤r < α+d，如图 3所示，区域R如图 3中阴影部分所示，则

$ \begin{align} & {{S}_{R}}=\left( {{S}_{{{O}_{2}}M{{p}_{1}}}}+{{S}_{{{O}_{1}}\overset\frown{M{{p}_{1}}}}}-{{S}_{{{O}_{1}}M{{p}_{1}}}} \right)+{{S}_{{{O}_{2}}\overset\frown{{{p}_{1}}{{p}_{2}}}}}+ \\ & \ \ \ \ \ \ \ \ \left( {{S}_{{{O}_{2}}{{p}_{2}}N}}+{{S}_{{{O}_{1}}\overset\frown{{{p}_{2}}N}}}-{{S}_{{{O}_{1}}{{p}_{2}}N}} \right)-\left( {{S}_{{{O}_{2}}MN}}+{{S}_{{{O}_{1}}NM}}-{{S}_{{{O}_{1}}\overset\frown{NM}}} \right). \\ \end{align} $

2.2 星座对地覆盖率计算

将卫星S_i的邻接结点集合记作V_i={v_i1, v_i2, …, v_im}，在目标区域Ω内的卫星邻接结点集合记作P_i，P_i={v_ij|v_ij∈V_i, v_ij∈Ω}，卫星的邻接多边形A_i和目标区域边界的交点集合记作Q_i，Q_i={v|v∈∂A_i∩∂Ω}.则卫星所属覆盖区域边界的顶点集合F_i=P_i∪Q_i，记作F_i={f_i1, f_i2, …, f_in}，∂Ω_i上的球面弧段集合为${E_i} = \left\{ {\mathop {{f_{i1}}{f_{i2}}}\limits^\frown ,\mathop {{f_{i2}}{f_{i3}}}\limits^\frown , \cdots ,\mathop {{f_{in}}{f_{i1}}}\limits^\frown } \right\}$，且在每条弧段中都记录了该弧段的所在球面圆圆心、半径，以及弧段边界点相对球面圆圆心的方向角.

以O_i为圆心，r为半径做球面圆Θ，与卫星所属覆盖区域Ω_i的相交区域记作R_i，R_i就是卫星S_i的实际覆盖区域.依次判断卫星所属覆盖区域边界∂Ω_i上的球面弧段${\mathop {{f_{i1}}{f_{i2}}}\limits^\frown ,\mathop {{f_{i2}}{f_{i3}}}\limits^\frown , \cdots ,\mathop {{f_{in}}{f_{i1}}}\limits^\frown }$和覆盖圆Θ的相交性，计算得到卫星实际覆盖区域R_i的边界顶点集合T_i，T_i={t_i1, t_i2, …, t_il}，以及∂R_i上的球面弧段集合${W_i} = \left\{ {\mathop {{t_{i1}}{t_{i2}}}\limits^\frown ,\mathop {{t_{i2}}{t_{i3}}}\limits^\frown , \cdots ,\mathop {{t_{il}}{t_{i1}}}\limits^\frown } \right\}$.

2.2.1 覆盖目标是全球区域

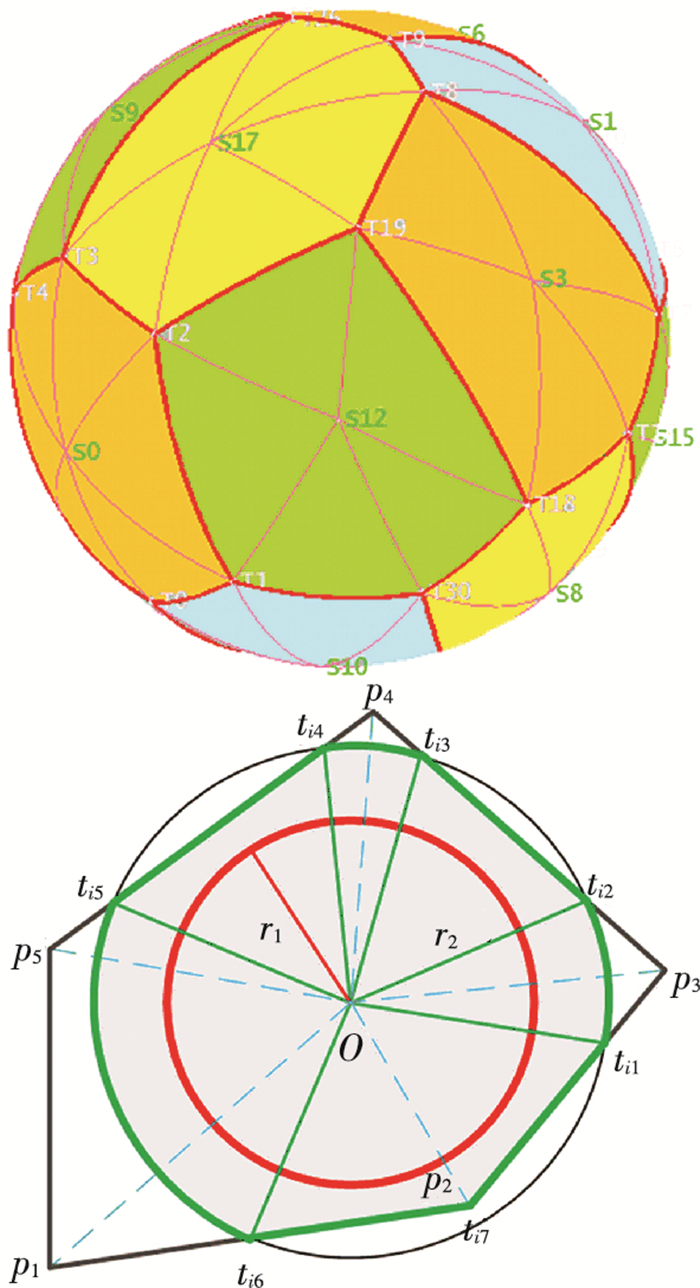
将全球区域按球面Voronoi图剖分方法进行划分，得到每颗卫星所属覆盖区域，如图 4所示，此时，卫星S_i的所属覆盖区域Ω_i就是其所属多边形区域A_i.图中，由顶点p₁, p₂, p₃, p₄, p₅围成的球面多边形区域就是卫星S_i的所属覆盖区域Ω_i，阴影部分是卫星对其所属覆盖区域的实际覆盖区域.

当卫星覆盖圆半径r=r₁时，卫星实际覆盖区域的边界顶点集合T_i=Φ，覆盖区域为以O为圆心，r₁为半径的球面圆.卫星O_i对其所属覆盖区域Ω_i的面积为

$ {S_{Ri}} = 2\pi R_{\rm{e}}^2\left( {1 - \cos r} \right). $

当卫星覆盖圆半径r=r₂时，卫星实际覆盖区域R_i如图 4中阴影部分所示，显然T_i≠Φ，且T_i={t_i1, t_i2, …, t_i7}，${W_i} = \left\{ {\mathop {{t_{i1}}{t_{i2}}}\limits^\frown ,\mathop {{t_{i2}}{t_{i3}}}\limits^\frown , \cdots ,\mathop {{t_{i7}}{t_{i1}}}\limits^\frown } \right\}$.依次计算由圆心O_i和弧段$\mathop {{t_{ij}}{t_{ik}}}\limits^\frown $围成的区域面积S_{i_jk}，则卫星S_i对其所属覆盖区域Ω_i的面积为

$ {{S}_{Ri}}=\sum\limits_{\overset\frown{{{t}_{ij}}{{t}_{ik}}}\in {{W}_{i}}}{{{S}_{i\_jk}}}. $

2.2.2 覆盖目标是球面凸多边形区域

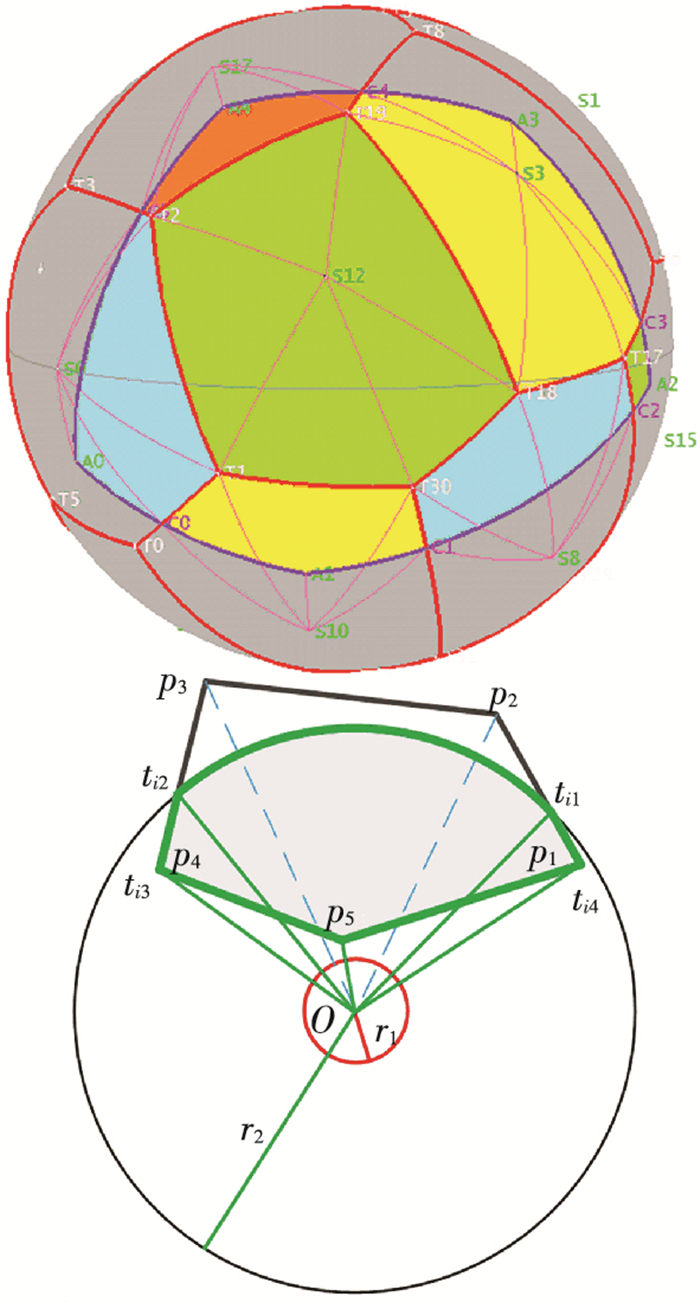
将球面凸多边形区域按球面Voronoi图剖分方法进行划分，得到每颗卫星所属覆盖区域，如图 5所示.当卫星星下点在覆盖目标区域Ω内部时，卫星对其所属覆盖区域的覆盖计算和星座对全球覆盖分析过程一样.当卫星星下点在覆盖区域外部时，卫星S_i的所属覆盖区域Ω_i是由顶点p₁, p₂, p₃, p₄, p₅围成的球面多边形区域.

当卫星覆盖圆半径r=r₁时，卫星实际覆盖区域的边界顶点集合T_i=Φ，卫星不能实现对其所属覆盖区域的覆盖，因此卫星O_i对其所属覆盖区域Ω_i的面积为

$ {{S}_{Ri}}=0. $

如果卫星实际覆盖区域的边界顶点集合T_i≠Φ，假定卫星覆盖圆半径r=r₂，卫星实际覆盖区域R_i如图 5中阴影部分所示，且T_i={t_i1, t_i2, …, t_i4}，${W_i} = \left\{ {\mathop {{t_{i1}}{t_{i2}}}\limits^\frown ,\mathop {{t_{i2}}{t_{i3}}}\limits^\frown , \cdots ,\mathop {{t_{i4}}{t_{i1}}}\limits^\frown } \right\}$.依次计算由圆心O_i和弧段$\mathop {{t_{ij}}{t_{ik}}}\limits^\frown $围成的有向区域面积S_{i_jk}，若卫星星下点O_i到弧段$\mathop {{t_{ij}}{t_{ik}}}\limits^\frown $所在球面圆圆心t_{i_jk}的球面距离dis (O_i, t_{i_jk}) < r，则S_{i_jk} > 0；否则，该面积取负值，即S_{i_jk} < 0.则卫星S_i对其所属覆盖区域Ω_i的面积为

$ {{S}_{Ri}}=\sum\limits_{\overset\frown{{{t}_{ij}}{{t}_{ik}}}\in {{W}_{i}}}{{{S}_{i\_jk}}}. $

2.2.3 覆盖目标是球面圆区域

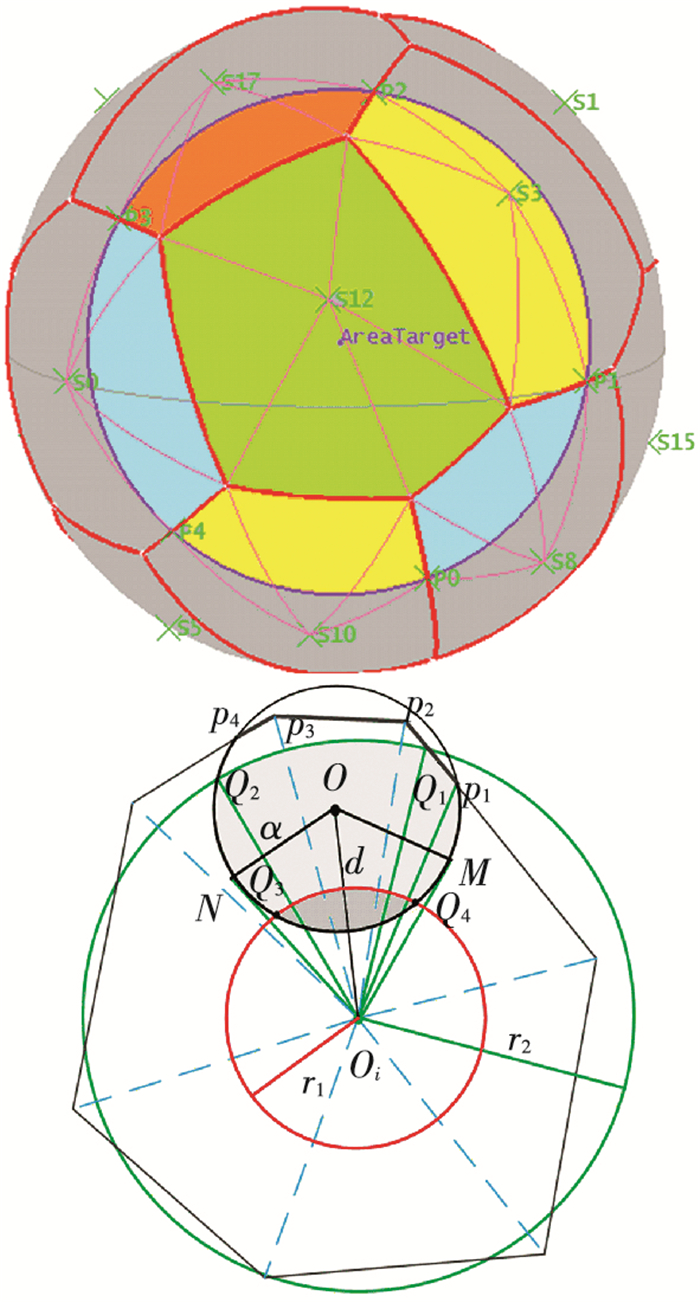
将以O为圆心，α为半径的球面圆形区域按球面Voronoi图剖分方法进行划分，得到每颗卫星所属覆盖区域，如图 6所示.当卫星星下点在覆盖目标区域Ω内部，即d≤α时，卫星对其所属覆盖区域的覆盖计算和星座对全球覆盖分析过程一样，与其不同的是卫星的实际覆盖区域边界中存在小圆弧段.当卫星星下点在覆盖区域外部，即d > α.

当卫星覆盖圆半径r≤d-α时，卫星实际覆盖区域的边界顶点集合T_i=Φ，卫星O_i对其所属覆盖区域Ω_i的面积为

$ {{S}_{Ri}}=0. $

当卫星覆盖圆半径d-α < r < d+α时，计算得到卫星实际覆盖区域边界顶点和弧段集合分别为：T_i={t_i1, t_i2, …, t_ik}，${W_i} = \left\{ {\mathop {{t_{i1}}{t_{i2}}}\limits^\frown ,\mathop {{t_{i2}}{t_{i3}}}\limits^\frown , \cdots ,\mathop {{t_{ik}}{t_{i1}}}\limits^\frown } \right\}$.卫星覆盖圆半径r=acos (cos d/cos α) 时，两球面圆相交于M, N两点，如果r≤acos (cos d/cos α)，则卫星对其所属覆盖区域的覆盖计算和覆盖能力计算分析过程一样，如果r > acos (cos d/cos α)，则将M, N两点加入集合T_i，得到新的覆盖区域顶点集合：T_i={M, t_i1, t_i2, …, t_ik, N}，球面弧段集合：${W_i} = \left\{ {\mathop {M{t_{i1}},}\limits^\frown \mathop {{t_{i1}}{t_{i2}}}\limits^\frown ,\mathop {{t_{i2}}{t_{i3}}}\limits^\frown , \cdots ,\mathop {{t_{ik}}N}\limits^\frown ,\mathop {NM}\limits^\frown } \right\}$.圆心O_i和弧段$\mathop {{t_{ij}}{t_{ik}}}\limits^\frown $围成的有向区域面积S_{i_jk}，若卫星星下点O_i到弧段$\mathop {{t_{ij}}{t_{ik}}}\limits^\frown $所在球面圆圆心t_{i_jk}的球面距离dis (O_i, t_{i_jk}) < r，则S_{i_jk} > 0；否则，该面积取负值，即S_{i_jk} < 0.卫星S_i对其所属覆盖区域Ω_i的面积为

$ {{S}_{Ri}}=\sum\limits_{\overset\frown{{{t}_{ij}}{{t}_{ik}}}\in {{W}_{i}}}{{{S}_{i\_jk}}}. $

2.2.4 覆盖目标是纬度带区间

纬度带区间为[l, u].当下纬度线l≥0时，星座对纬度带区域的覆盖计算可以分解为对以 (0, π) 为圆心，π/2-l为半径的圆的覆盖面积S_l，和以 (0, π) 为圆心，π/2-u为半径的圆的覆盖面积S_u，星座对纬度带区域的覆盖面积S=S_l-S_u.

当下纬度线u≤0时，星座对纬度带区域的覆盖计算可以分解为对以 (0, π) 为圆心，π/2-l为半径的圆的覆盖面积S_l，和以 (0, π) 为圆心，π/2-u为半径的圆的覆盖面积S_u，星座对纬度带区域的覆盖面积S=S_u-S_l.

当l < 0，且u > 0时，星座对纬度带区域的覆盖计算可以分解为对全球的覆盖面积S_A和以 (0, π) 为圆心，π/2-l为半径的圆的覆盖面积S_l和以 (0, π) 为圆心，π/2-u为半径的圆的覆盖面积S_u，星座对纬度带区域的覆盖面积S=S_A-S_l-S_u.

3 实例分析

以参数为 (T/P/F)=(36/4/1) 的Walker星座为例，卫星轨道高度为H=1 300 km.定义覆盖目标1为球面多边形区域，球面多边形的顶点集合为 (63°, 54°), (73°, 3°), (126°, 3°), (156°, 44°), (120°, 68°).覆盖目标2为球面圆区域，球面圆中心为 (θ, φ)=(63°, 54°)，半径为α=20°.卫星对目标最小观测仰角约束为γ_min=10°，分别计算在一个卫星轨道周期内，该星座对该球面多边形区域和球面圆形区域的覆盖能力.

3.1 星座对地覆盖率计算

首先，对星座的空间几何构形进行球面Delaunay三角网剖分，并在此基础上，计算卫星的所属覆盖区域.以覆盖目标是球面圆区域为例.

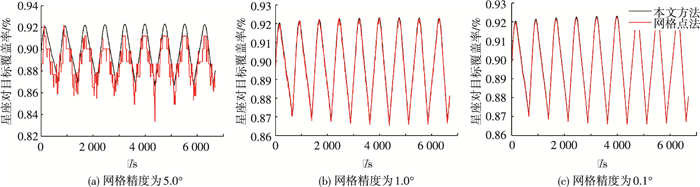
图 7所示是网格划分精度分别为5.0°, 1.0°, 0.1°时，整个仿真周期内星座对目标区域的覆盖率计算结果与本文所提方法计算结果的对比.图中，黑色实线为采用本文提出的球面几何剖分法计算得到的星座对目标区域的覆盖率，红色实线为采用网格点划分法计算得到的星座对目标区域的覆盖率.

比较图 7中两种方法的计算结果，并计算对应的覆盖率偏差，结果如图 8所示.

分别对比图 8的计算结果，可见网格划分精度越小，网格点法计算结果越精确，且和本文所提出方法的计算结果偏差也越小，反映了本文所提出方法的正确性.

当网格点划分精度为1.0°时，每个网格将代表地球表面上面积为 (π·R_e/180)² km²的区域.将目标区域按照网格点划分进行星座对地覆盖率计算，分析进行一次星地覆盖计算的计算时长随目标区域面积和划分精度的关系.当网格划分精度为0.1°，覆盖目标是全球区域时，进行一次覆盖计算的时间约为88.3 s；而采用本文提出的星座空间几何构形剖分的方法进行一次星地覆盖计算只需要约21 ms，并且目标区域的形状和大小对计算时长均没有影响，反映了本文所提出方法在时间复杂度上的高效性.

3.2 结果分析

通过对上述实验的对比分析，计算结果验证了本文基于星座空间构形几何剖分进行星座对地覆盖计算方法的正确性和高效性.尤其当目标区域较大且对星座覆盖精度要求较高时，传统的基于网格点划分的方法往往是不可行的.并且在仿真周期内，当星座中存在两颗星在某一时刻相撞时，通过本文的星座空间构形几何剖分法可以检测出来，且不影响剖分方法和计算结果.

4 结论

1) 采用经典的网格点或者条带划分法进行覆盖率计算，得到的星座对地覆盖率精度是基于网格点或者条带的划分精度的；而网格点或条带划分的越细，对应的计算时间复杂度会很高.对比之下，本文提出的基于星座空间构形几何剖分进行星座对地覆盖计算是一种确定性方法，计算结果是精确值，更加可靠，且计算效率有显著提高.

2) 基于Delaunay三角网和Voronoi图特性，对任意时刻卫星星座在地球表面投影点的集合进行划分，且通过定义每颗卫星所属覆盖区域，将星座覆盖问题简化为单星覆盖问题，可以精确快速计算星座中卫星对目标区域的覆盖能力的时变特性，以及在实现对目标区域的覆盖过程中每颗星的重要性，并且该方法适用于对任意类型的地面目标区域覆盖计算.