在一些特定的背景下,为了提高我方飞行器的生存能力,需要设计回避目标飞行器的制导律.这种回避制导律需要知道关于目标飞行器的制导律、参数和状态的完整信息.因此,需要一种针对目标飞行器制导律、参数和状态的辨识估计方法,在我方飞行器与目标飞行器相遇过程中进行辨识.从目标飞行器外部测量数据出发,对其制导律进行辨识,对于飞行器制导规律的优化设计、效能评估、有效观测、轨迹预测等方面具有重要的理论和应用价值.
目标飞行器可以从已有的制导律中选取一种制导律,例如,比例导引律、滑模制导律、最优制导律等.制导律识别问题则是从目标飞行器外部观测数据出发,对未知的目标飞行器制导律进行辨识和参数估计.
由于制导律的多样性,其识别问题的难点在于构造统一的通用数学模型,对制导行为进行描述.Grove等[1]在认定目标飞行器采用比例导引律的前提下,以比例导引系数作为未知量建立观测数据方程,通过求解制导控制量方程得到制导律的参数.Lin等[2]指出,对于未知的制导律可以假设为比例导引律,通过调整比例导引系数来拟合任意未知的制导律.Horton[3]则使用卡尔曼滤波器和神经网络相结合的方法对飞行器自身的空气动力学参数的进行实时识别.Li等[4]归纳总结了针对运动目标轨迹的跟踪方法,讨论了利用动力学模型对机动目标的建模和轨迹跟踪方法.在其他类似的研究中,Raviadra等[5]使用卡尔曼滤波器对目标飞行器的轨迹进行识别.Kunwar等[6]研究了移动目标拦截过程中的轨迹规划问题.
综合上述研究结果可以看出,对目标飞行器制导行为的识别以及对识别结果的利用目前需要进一步深入研究.本文利用了通用的隐式制导函数方法对制导行为模式进行统一描述,并且给出了采用时变制导系数的近似模型来逼进隐式制导函数.在该数学模型的基础上,利用低通滤波与卡尔曼滤波相结合的频域分离自适应卡尔曼滤波方法 (frequency divided adaptive Kalman filter, FD-AKF) 对观测数据进行实时处理分析,并得到目标飞行器的制导律识别结果.
由于采用了低通滤波与卡尔曼滤波相结合的方法,测量信息中的噪声得到了更好地抑制.为了在动态噪声或测量噪声统计特性未知情况下设计卡尔曼滤波器,Yang等[7]提出了需要预知残差向量和预测向量的理论协方差矩阵自适应参数调整方法.Huang等[8]提出的实时切换预定模型以适应噪声参数变化的方法.Kim等[9]采用自适应衰减滤波器使用遗忘因子对统计信息进行在线分析增强滤波方法的稳定性.Karavasilis等[10]通过动态调整状态切换矩阵的方法,完成滤波器对输入的主动适应和调整.Chai等[11]整合了神经网络的学习适应能力和滤波器的估计识别能力.Kim等[12]利用自适应卡尔曼滤波器校正小波神经网络的学习速率,以保证神经网络的稳定收敛.Wang等[13]将Sage-Husa自适应滤波器与卡尔曼滤波器整合,利用自适应滤波器设定滤波器的噪声水平参数.Yang[14]则指出自适应卡尔曼滤波器的核心是对状态噪声和测量噪声方差的实时估计.
已有研究表明,对预测噪声和测量噪声的方差水平识别需要同时进行,才能够有效地保证算法的收敛性[14],但是这种做法会带来大量的计算,而基于窗口方法和遗忘因子设计的滤波器,其中的大量参数需要根据实际情况和经验值才能确定,不利于算法和方法的推广.本文提出的低通滤波与卡尔曼滤波相结合的FD-AKF方法利用了系统中有效信号与测量噪声在频域上的不同分布特性,使用低通滤波器快速确定测量噪声方差水平,同时保持了有效信号不受影响.
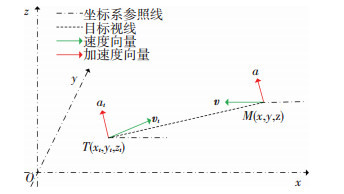
1 制导律识别问题三维空间中的制导问题如图 1所示.其中:惯性参考坐标系为末制导初始时刻的视线坐标系相对于惯性空间固化不动;M为我方飞行器,其在惯性参照系中的坐标为x, y, z;T为非合作目标飞行器,其在惯性参照系里面的坐标为xt, yt, zt;符号v、vt分别为我方飞行器和目标飞行器的速度向量.目标飞行器根据两者的相对运动关系和自身的制导律,调整自身的加速度,从而达到命中我方飞行器的目的.
|
图 1 制导问题 Figure 1 Illustration of guidance problem |
根据外在的测量参数到机动加速度之间的映射关系,未知的制导律就可以简化并抽象成一个隐式的待识别的制导函数[3]:
| $ \overrightarrow a = {a_t}\left( {\dot R,\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}} \right). $ | (1) |
式中:函数的输出
分析现有制导律设计结果可得出,制导过程中目标飞行器的机动加速度可以近似为与接近速度和视线转率的乘积成比例关系,所以识别过程中引入参数Ny和Nz.在目前的研究阶段,采取简化的数学模型将函数关系假设为
| $ \overrightarrow a = \left[ {\begin{array}{*{20}{c}} 0\\ {{N_y}\dot R{\mathit{\Omega }_y}}\\ {{N_z}\dot R{\mathit{\Omega }_z}} \end{array}} \right], $ | (2) |
制导律的识别具体化为未知的等效参数Ny和Nz的识别,它们甚至可以是变化的.
2 制导律识别算法 2.1 基于扩展卡尔曼滤波的识别算法 2.1.1 状态方程的建立选取状态向量为
| $ \mathit{\boldsymbol{X = }}\left\{ \begin{array}{l} x,y,z,{\mathit{\boldsymbol{v}}_x},{\mathit{\boldsymbol{v}}_y},{\mathit{\boldsymbol{v}}_z};\\ {x_t},{y_t},{z_t},{\mathit{\boldsymbol{v}}_{xt}},{\mathit{\boldsymbol{v}}_{yt}},{\mathit{\boldsymbol{v}}_{zt}};\\ {a_{xt}},{a_{yt}},{a_{zt}},{N_y},{N_z}. \end{array} \right. $ | (3) |
则不难写出系统的状态方程:
| $ \left\{ \begin{array}{l} \dot x = {\mathit{\boldsymbol{v}}_x},\dot y = {\mathit{\boldsymbol{v}}_y},\dot z = {\mathit{\boldsymbol{v}}_z};\\ {{\mathit{\boldsymbol{\dot v}}}_x} = 0,{{\mathit{\boldsymbol{\dot v}}}_y} = 0,{{\mathit{\boldsymbol{\dot v}}}_z} = 0,\\ {{\dot x}_t} = {\mathit{\boldsymbol{v}}_{xt}},{{\dot y}_t} = {\mathit{\boldsymbol{v}}_{yt}},{{\dot z}_t} = {\mathit{\boldsymbol{v}}_{zt}};\\ {{\mathit{\boldsymbol{\dot v}}}_{xt}} = {a_{xt}},{{\mathit{\boldsymbol{\dot v}}}_{yt}} = {a_{yt}},{{\mathit{\boldsymbol{\dot v}}}_{zt}} = {a_{zt}},\\ {{\dot a}_{xt}} = \left( {{u_{xt}} - {a_{xt}}} \right)/\tau + {\omega _{axt}};\\ {{\dot a}_{yt}} = \left( {{u_{yt}} - {a_{yt}}} \right)/\tau + {\omega _{ayt}};\\ {{\dot a}_{zt}} = \left( {{u_{zt}} - {a_{zt}}} \right)/\tau + {\omega _{azt}};\\ {{\dot N}_y} = {\omega _{Ny}},{{\dot N}_z} = {\omega _{{N_z}}}. \end{array} \right. $ |
式中:uxt、uyt、uzt分别为目标飞行器制导律控制下的加速度指令;τ为目标飞行器过载回路的时间常数;ωNy、ωNz分别为状态迁移引入的动态噪声.该方程可以写作状态方程:
| $ \mathit{\boldsymbol{\dot X = }}f\left( {\mathit{\boldsymbol{X,}}\tilde \omega } \right). $ |
滤波器的观测向量由飞行器的位置、速度、目标飞行器的位置、速度、机动加速度构成.上述观测结果向量,实际工程上可以通过组网定位等技术对目标飞行器进行测量,并且利用卡尔曼滤波的方法对其机动加速度进行实时处理.本文中将忽略具体的实现过程,假设测量结果能够直接获得,作为识别算法的原始测量内容参与识别.制导过程中需要的相对运动参数,如相对位置和视线转率等参数可以借助原始测量值间接获得,对制导行为的识别转化成对复杂等效制导参数的识别.
| $ \mathit{\boldsymbol{Z}} = \left\{ \begin{array}{l} x + {\varepsilon _x},y + {\varepsilon _y},z + {\varepsilon _z};\\ {\mathit{\boldsymbol{v}}_x} + {\varepsilon _{dx}},{\mathit{\boldsymbol{v}}_y} + {\varepsilon _{dy}},{\mathit{\boldsymbol{v}}_z} + {\varepsilon _{dz}};\\ {x_t} + {\varepsilon _{xt}},{y_t} + {\varepsilon _{yt}},{z_t} + {\varepsilon _{zt}};\\ {\mathit{\boldsymbol{v}}_{xt}} + {\varepsilon _{dxt}},{\mathit{\boldsymbol{v}}_{yt}} + {\varepsilon _{dyt}},{\mathit{\boldsymbol{v}}_{zt}} + {\varepsilon _{dzt}};\\ {a_{xt}} + {\varepsilon _{ax}},{a_{yt}} + {\varepsilon _{ay}},{a_{zt}} + {\varepsilon _{az}}, \end{array} \right. $ |
式中:εx、εy、εz分别为位置向量的观测噪声;εdx、εdy、εdz分别为速度向量的观测噪声;εxt、εyt、εzt分别为目标飞行器位置向量的观测噪声;εdxt、εdyt、εdzt分别为目标飞行器速度向量的观测噪声;εax、εay、εaz分别为目标飞行器机动加速度的观测噪声.
2.1.3 扩展卡尔曼滤波算法 (EKF)针对系统 (2),推广卡尔曼滤波算法 (EKF)[5, 7, 9]为
| $ \left\{ \begin{array}{l} {{\hat X}_{K + 1/K}} = {{\hat X}_{K/K}} + f\left( {{{\hat X}_{K/K}},\tilde \omega } \right)\Delta t + \frac{1}{2}Ff\left( {{{\hat X}_{K/K}},\tilde \omega } \right)\Delta {t^2},\\ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{K + 1/K}} = I + F\Delta t + \frac{1}{2}F\Delta {t^2},\\ {\mathit{\boldsymbol{P}}_{K + 1/K}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{K + 1/K}}{P_{K/K}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{K + 1/K}^{\rm{T}} + {\mathit{\boldsymbol{Q}}_k},\\ {\mathit{\boldsymbol{K}}_{K + 1}} = {\mathit{\boldsymbol{P}}_{K + 1/K}}H_{K + 1}^{\rm{T}}{\left( {{H_{k + 1}}{\mathit{\boldsymbol{P}}_{K + 1/K}}H_{k + 1}^{\rm{T}} + {\mathit{\boldsymbol{R}}_{K + 1}}} \right)^{ - 1}},\\ {{\hat X}_{K + 1/K + 1}} = {{\hat X}_{K + 1|K}} + {\mathit{\boldsymbol{K}}_{K + 1}}\left( {{Z_{K + 1}} - {H_{K + 1}}{{\hat X}_{K + 1|K}}} \right),\\ {\mathit{\boldsymbol{P}}_{K + 1/K + 1}} = \left( {I - {\mathit{\boldsymbol{K}}_{K + 1}}{H_{K + 1}}} \right){\mathit{\boldsymbol{P}}_{K + 1/K}}. \end{array} \right. $ |
式中:
| $ F = \frac{{\partial f\left[ {X\left( t \right)} \right]}}{{\partial X\left( t \right)}}\left| {_{X = {{\hat X}_{K/K}}}} \right.;{H_{K + 1}} = H. $ |
在给定
在系统 (1) 中
| $ \left\{ \begin{array}{l} {u_{xt}} = 0,\\ {u_{xt}} = {N_y}\dot R{\mathit{\Omega }_y},\\ {u_{zt}} = {N_z}\dot R{\mathit{\Omega }_z}, \end{array} \right. $ |
其中:
| $ \begin{array}{*{20}{c}} {\dot R = \frac{{{r_x}{\mathit{\boldsymbol{v}}_{rx}} + {r_y}{\mathit{\boldsymbol{v}}_{ry}} + {r_z}{\mathit{\boldsymbol{v}}_{rz}}}}{{\sqrt {r_x^2 + r_y^2 + r_z^2} }},}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_y} = \frac{{\left( {r_x^2 + r_z^2} \right){\mathit{\boldsymbol{v}}_{ry}} - {r_y}\left( {{r_x}{\mathit{\boldsymbol{v}}_{rx}} + {r_z}{\mathit{\boldsymbol{v}}_{rz}}} \right)}}{{\left( {r_x^2 + r_y^2 + r_z^2} \right)\sqrt {r_x^2 + r_z^2} }},}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_y} = \frac{{\left( {r_x^2 + r_z^2} \right){\mathit{\boldsymbol{v}}_{ry}} - {r_y}\left( {{r_x}{\mathit{\boldsymbol{v}}_{rx}} + {r_z}{\mathit{\boldsymbol{v}}_{rz}}} \right)}}{{\left( {r_x^2 + r_y^2 + r_z^2} \right)\sqrt {r_x^2 + r_z^2} }}.} \end{array} $ |
式中,rx=x-xt,ry=y-yt,rz=z-zt,vrx= vx-vxt,vry= vy-vyt,vrz= vz-vzt.[15]
观测方程 (3) 以观测矩阵形式描述,则
| $ H = \left[ {\begin{array}{*{20}{c}} {{I_3}} & {} & {} & {} & {} & 0 & 0\\ {} & {{I_3}} & {} & {} & {} & 0 & 0\\ {} & {} & {{I_3}} & {} & {} & 0 & 0\\ {} & {} & {} & {{I_3}} & {} & 0 & 0\\ {} & {} & {} & {} & {{I_3}} & 0 & 0 \end{array}} \right]. $ |
由于制导律辨识模型具有不确定性,通过对状态噪声和观测噪声协方差矩阵的实时处理来补偿模型的不确定性.因为目标飞行器有主动的机动行为,特别的,当目标飞行器制导行为中的等效参数变化复杂时,系统状态的预测上会产生较大的误差.
已有研究中Sage-Husa算法[14]和其他改进的算法[16-17]中,都是以此为出发点,对状态噪声和测量噪声进行方差水平的识别.根据观测值与处理值之间的差值,就可以获得当前一次迭代的状态噪声和测量噪声估计值,然后使用窗口法则或者渐消法则,完成方差水平的计算.
2.2.1 低通滤波的理论依据根据采样定理,卡尔曼滤波器的迭代计算频率一定要大于有效信号频率的2倍.由于状态噪声产生于每一步预报计算,观测噪声产生于每一步观测测量,他们的特征频率必然接近于卡尔曼滤波的计算频率和观测频率.系统中的状态噪声和测量噪声的能量密度集中在频谱的高端部分.由于有效信号和噪声的能量分别分布在低频段和高频段,可以通过低通数字滤波的方法降低噪声的影响.
经过快速傅里叶变换,由图 2单边带频域能量分布中可以看出,有效的系统信号与噪声信号在频域出现了明显的分离.低频部分代表有效数据的变化,而高频部分则来自于状态噪声或者观测噪声.通过低通滤波,在预测输出的数据序列中提出有效数据,同时将预测输出与低通滤波以后的差值作为噪声的估计,进行后续的计算.

|
图 2 模型预测向量的频域分析结果 Figure 2 Energy distribution in frequency domain |
同理,Zk和Vk也可以通过低通滤波的方法进行分离.
2.2.2 噪声向量的低通滤波分离法滤波过程中,由于Φk, k-1 Xk-1的频率低于低通滤波截止频率,所以有LPF (Φk, k-1Xk-1)≈ Φk, k-1Xk-1.与此同时,Wk的频率高于低通滤波截止频率,所以有LPF (Wk)≈0.那么,对迭代过程中得到的预测数据进行低通滤波处理,将会得到:
| $ \begin{array}{l} {\rm{LPF}}\left( {{X_k}} \right) = {\rm{LPF}}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k,k - 1}}{X_{k - 1}} + {W_k}} \right) \approx \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{LPF}}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k,k - 1}}{X_{k - 1}}} \right) \approx {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k,k - 1}}{X_{k - 1}}. \end{array} $ |
于是Wk≈Xk-LPF (Xk).
同理,Vk≈Zk-LPF (Zk),低通滤波器的迭代计算公式LPF:yt=yt-1*(1-α)+xt*α,其中α为低通滤波参数,如果对应截止频率为f的时候,α的计算公式为α=f*2πdt,dt为采样周期.
2.2.3 方差水平的估计Wk和Vk的近似序列获得以后,可以采用窗口方法或者渐消滤波方法计算方差水平.本文提出了再次低通滤波的方法对Wk和Vk的方差水平进行识别.Wk和Vk虽然本身是高频的,但是其方差水平的变化频率却远低于其自身的频率,所以文中采用了低通滤波的方法对其方差水平进行估计.
以Wk为例,k时刻采样值的方差水平σk=Wk*WkT,与上述同样的低通滤波设计方法,如果能够根据物理意义确定方差水平变化频率为f′的话,可以得到Wk的方差水平估计的迭代计算公式
在低通滤波方法中,Q、R的正定性能够得到保证.但是随着滤波器的迭代计算,系统的状态噪声会逐渐缩减.导致Q矩阵虽然是主对角阵,但是个别分量的数值特别的小,以至于矩阵的条件数非常大,影响后续求逆阵过程中的数值计算精度.本文借鉴已有的保护策略,为Q、R设定了条件数保护措施,即
| $ \begin{array}{l} \mathit{\boldsymbol{Q}} = \mathit{\boldsymbol{Q}} + 0.5 * I,\\ \mathit{\boldsymbol{R}} = \mathit{\boldsymbol{R}} + 0.5 * I. \end{array} $ |
保护措施的特点是叠加一个基础的保护矩阵,而不是使用条件判断.当Q的值大于保护矩阵数值的时候,保护矩阵会被真实数据所掩盖;当Q的值小于保护矩阵数值的时候,保护矩阵保证Q的分量不小于设定的保护范围.
3 结果和分析仿真的过程中假设:1) 忽略任何外在场的影响,目标飞行器具有理想的轨控发动机,能够产生连续推力.2) 我方飞行器和目标飞行器均具有理想的姿态控制系统,保持飞行器的姿态主轴与速度向量相重合.3) 执行识别任务的飞行器被目标飞行器追踪过程中,能够获得目标飞行器动力学测量信息.
飞行器的空间初始位置 (x y z) 为200 000, 200 000, 200 000 m; 初始速度 (vx vy vz) 为-3 000, -3 000, -5 000 m/s;目标飞行器的空间初始位置 (x y z) 为0, 0, 0 m; 初始速度 (vx vy vz) 为3 000, 3 500, 4 500 m/s.我方飞行器做匀速运动,目标飞行器按照其制导律控制逻辑,产生机动加速度,借以完成拦截任务.
本文将以Sage-Husa估计器为基础的自适应Kalman滤波识别算法,与文中提出的FD-AKF进行对比以检验该方法的有效性.Sage-Husa估计器算法中窗口深度设定为5,使用RAE方式对预测噪声和测量噪声的方差进行估计.FD-AKF只有一个低通滤波参数需要设定,由于待识别目标的运动特征频率不会超过10 Hz,所以算法的低通滤波截止频率设定为小于10 Hz的一个经验值,2.5 Hz.
仿真过程中在多种不同的制导律配置情况下,对制导律识别的效果进行验证.
情况1 当目标飞行器使用固定的制导律参数N=4.83的时候,等效制导系数的识别结果如图 3、4所示.

|
图 3 FD-AKF对固定制导参数的识别 Figure 3 FD-AKF against fixed guidance parameter |

|
图 4 Sage-Husa算法对固定制导参数的识别 Figure 4 Sage-Husa against fixed guidance parameter |
图 3、4中,上部的蓝色曲线为俯仰通道制导参数Ny的理论值,红色曲线为识别结果.下部的紫色曲线为偏航通道制导参数Nz的理论值,青色曲线为识别结果.可以看出,对于固定的制导系数,两种算法都能够完成很好的识别,结果的误差水平都在1%以内.但是,在仿真后期,随着目标飞行器机动加速度逐渐衰减,Sage-Husa算法出现了发散.
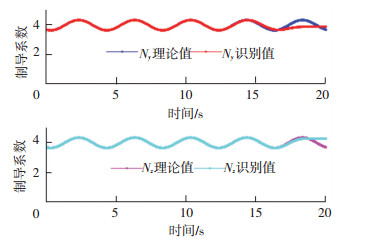
情况2 目标飞行器等效制导行为参数随着时间推移以正弦规律变化.实际中可能不会出现,但是这种虚拟的制导律可以验证识别算法对处于变化中的制导规律的识别能力.
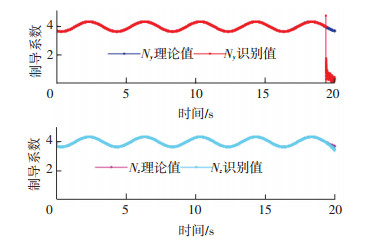
图 5、6中可以看出,当制导参数发生动态变化的时候,FD-AKF算法和Sage-Husa算法都能够保持跟踪能力.但是,在仿真后期,由于目标飞行器机动加速度逐渐衰减,Sage-Husa算法出现了发散.
|
图 5 FD-AKF对时变制导参数的识别结果 Figure 5 FD-AKF against varying guidance parameter |
|
图 6 Sage-Husa对时变制导参数的识别结果 Figure 6 Saga-Husa against varying guidance parameter |
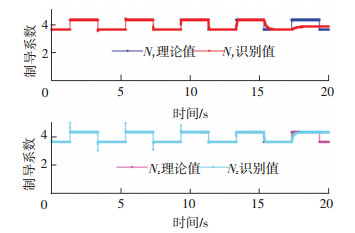
情况3 目标飞行器等效制导行为参数发生突变.
为进一步说明滤波器对于变化的制导律的识别能力,设计了制导参数会发生突变的制导律,用以检验识别算法跟踪制导律变化的能力.
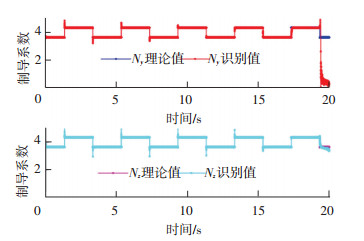
图 7、8中可以看出,当制导参数发生动态切换的时候,FD-AKF算法和Saga-Husa算法都能够保持跟踪能力.但是,Sage-Husa在制导参数切换的时刻,识别结果出现了明显的跳变.而且在仿真后期,随着目标飞行器的机动加速度逐渐衰减,Sage-Husa算法出现了发散,而FD-AKF则能够保持稳定.
|
图 7 FD-AKF对跳变制导参数的识别结果 Figure 7 FD-AKF against shifting guidance parameter |
|
图 8 Sage-Husa对跳变制导参数的识别结果 Figure 8 Saga-Husa against shifting guidance parameter |
从仿真结果中可以看出,当目标飞行器的制导规律不发生变化的时候,FD-AKF和Sage-Husa算法都能够很好的完成目标行为规律的识别,制导律参数的收敛速度很快,而且最终的相对误差稳定在1%以内.当目标飞行器的制导行为规律发生变化的时候,文中提出的FD-AKF在收敛速度和跟随变化的性能上明显优于Sage-Husa算法,原因在于FD-AKF算法可以直接从预测数据和测量数据出发,分离出高频预测噪声和测量噪声的同时,保留了低频率的有效数据变化规律.所以,目标的制导行为规律发生变化的时候,FD-AKF算法能够及时响应,正确跟踪其变化过程.
无论是FD-AKF还是Sage-Husa算法,当目标飞行器的过载低于1 g以后,制导行为的识别效果明显变差.
情况4 目标飞行器采取BANG-BANG变结构制导律.
为进一步检验FD-AKF对目标飞行器制导行为的辨识效果,假设目标飞行器采用Bang-Bang变结构制导律.由于飞行器的姿态控制系统令飞行器体坐标系跟踪视线坐标系,因此,设计制导律为:
| $ \begin{array}{l} {a_{{y_1}}} = \left\{ \begin{array}{l} M,{{\dot q}_\varepsilon } > {\delta _\varepsilon };\\ 0,\left| {{{\dot q}_\varepsilon }} \right| < {\delta _\varepsilon };\\ - M,{{\dot q}_\varepsilon } < - {\delta _\varepsilon }. \end{array} \right.\\ {a_{{z_1}}} = \left\{ \begin{array}{l} M,{{\dot q}_\beta } > {\delta _\beta };\\ 0,\left| {{{\dot q}_\beta }} \right| < {\delta _\beta };\\ - M,{{\dot q}_\beta } < - {\delta _\beta }. \end{array} \right. \end{array} $ |
式中:ay1为沿弹体坐标系oy1轴方向上的加速度;az1为沿弹体坐标系oz1轴方向上的加速度;M=const.>0为理想的轨控发动机推力作用在导弹上产生的加速度.Bang-Bang变结构制导律由于采用了非线性的控制策略,在切换面附件迁移的过程中,等效时变制导参数会发生高频率的跳变.由于这种跳变的存在,FD-AKF对Bang-Bang制导律等效制导参数识别过程中,低通滤波的截止频率调高到50 Hz.
|
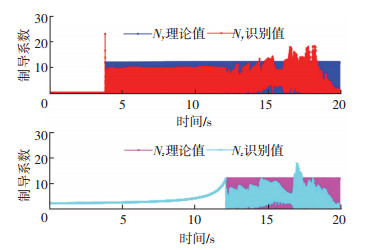
图 9 FD-AKF对Bang-Bang变结构制导律识别 Figure 9 FD-AKF against Bang-Bang guidance law |
|
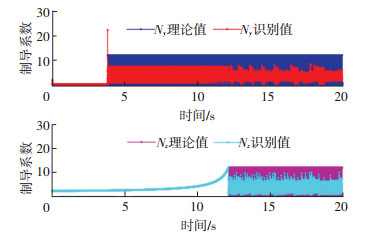
图 10 Sage-Husa对于Bang-Bang变结构制导律的识别 Figure 10 Sage-Husa against Bang-Bang guidance law |
图 9、10中,上部的蓝色和紫色曲线为等效制导参数Ny、Nz的理论值,理论值是根据控制加速度和接近速度视线转率换算得来的.红色和青色曲线为对应的识别结果.可以看出,FD-AKF算法对等效时变制导参数的识别明显优于Sage-Husa算法的识别结果.
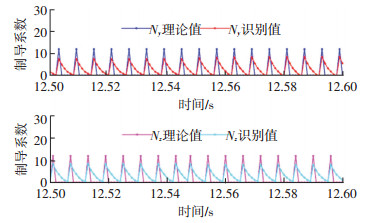
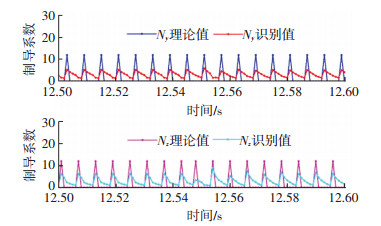
图 11、12分别是图 9、10俯仰通道的局部放大.可以看出,对于蓝色曲线表示出的等效制导系数理论值在0~12之间的变化,FD-AKF识别结果在0~12之间跟随,而Sage-Husa的识别结果的最大、最小值分别为7和2.偏航通道的局部放大图可以得到类似的结果.
|
图 11 FD-AKF对于Bang-Bang变结构制导律的识别结果 (局部放大) Figure 11 FD-AKF against Bang-Bang guidance law (partial enlarged) |
|
图 12 Sage-Husa对于Bang-Bang变结构制导律的识别结果 (局部放大) Figure 12 Sage-Husa against Bang-Bang guidance law (partial enlarged) |
1) 通用制导模型中引入时变的等效制导系数解决了数学模型不统一的问题.在此基础上,低通滤波和卡尔曼滤波相结合的频域分离自适应卡尔曼滤波算法 (FD-AKF) 可以完成对制导律的在线识别.仿真实验结果表明,在飞行器机动的情况下,本文提出的制导律识别方法能够从比例导引和Bang-Bang变结构制导律的观测数据出发,对目标飞行器的制导律完成有效的快速识别.
2) 在本文工作的基础上,可以进一步通过实验验证制导律FD-AKF识别算法对于更复杂制导律的识别效果.影响制导律识别效果的各种因素也需要进一步确认.
| [1] | GROVES G W, BLAIR W D, HOFFMAN S. Some concepts for trajectory prediction for ship self defense[J]. Proceedings of the American Control Conference, 1995, 6: 4121-4126. DOI: 10.1109/ACC.1995.532707 |
| [2] | LIN C S, RAETH P G. Prediction of missile trajectory[C]//Proceedings of the IEEE International Conference on Systems, Man and Cybernetics Intelligent Systems for the 21st Century.[S.l.]: IEEE, 1995: 2558-2563. DOI: 10.1109/ICSMC.1995.538167. |
| [3] | HORTON M P. Real-time identification of missile aerodynamics using a linearised kalman filter aided by an artificial neural network[J]. IEEE Transactions on Control Theory and Applications, 1997, 144(4): 299-308. DOI: 10.1049/ip-cta:19971125 |
| [4] | LI X R, JILKOV V P. Survey of maneuvering target tracking. Part Ⅱ: motion models of ballistic and space targets[J]. IEEE Transactions on Aerospace & Electronic Systems, 2010, 46(1): 96-119. DOI: 10.1109/TAES.2010.5417150 |
| [5] | RAVINDRA V C, BAR-SHALOM Y, WILLETT P. Projectile identification and impact point prediction[J]. IEEE Transactions on Aerospace & Electronic Systems, 2010, 46(4): 2004-2021. DOI: 10.1109/TAES.2010.5595610 |
| [6] | KUNWAR F, SHERIDAN P K, BENHABIB B. Predictive guidance-based navigation for mobile robots: a novel strategy for target interception on realistic terrains[J]. Journal of Intelligent & Robotic Systems, 2010, 59(3/4): 367-398. DOI: 10.1007/s10846-010-9401-3 |
| [7] | YANG Yuanxi, GAO Weiguang. An optimal adaptive kalman filter[J]. Journal of Geodesy, 2006, 80(4): 177-183. DOI: 10.1007/s00190-006-0041-0 |
| [8] | HUANG Guanwen, ZHANG Qin. Realtime estimation of satellite clock offset using adaptively robust Kalman Filter with classified adaptive factors[J]. GPS Solutions, 2012, 16(4): 531-539. DOI: 10.1007/s10291-012-0254-z |
| [9] | KIM K H, JEE G I, PARK C G, et al. The stability analysis of the adaptive fading extended Kalman filter using the innovation covariance[J]. International Journal of Control Automation & Systems, 2009, 7(1): 49-56. DOI: 10.1007/s12555-009-0107-x |
| [10] | KARAVASILIS V, NIKOU C, LIKAS A. Visual tracking by adaptive kalman filtering and mean shift[M]. Berlin, Heidelberg: Springer-Verlag, 2010: 153-162. |
| [11] | CHAI Lin, YUAN Jianping, FANG Qun, et al. Neural network aided adaptive kalman filter for multi-sensors integrated navigation[M]. Berlin, Heidelberg: Springer-Verlag, 2004: 381-386. |
| [12] | KIM K J, JIN B P, CHOI Y H. The adaptive learning rates of extended kalman filter based training algorithm for wavelet neural networks[M]. Berlin, Heidelberg: Springer-Verlag, 2006: 327-337. |
| [13] | WANG Sisi, WANG Lijun. Maneuvering target tracking based on adaptive square root cubature kalman filter algorithm[M]. Berlin, Heidelberg: Springer-Verlag, 2012: 901-908. |
| [14] | YANG Yuanxi. Adaptively robust Kalman Filters with applications in navigation[M]. Heidelberg: Springer-Verlag, 2010. |
| [15] |
周荻.
寻的导弹新型导引规律[M]. 北京: 国防工业出版社, 2012.
ZHOU Di. New guidance laws for homing missile[M]. Beijing: National Defense Industry Press, 2012. |
| [16] | LIN S G. Assisted adaptive extended Kalman filter for low-cost single-frequency GPS/SBAS kinematic positioning[J]. GPS Solutions, 2015, 19(2): 215-223. DOI: 10.1007/s10291-014-0381-9 |
| [17] | ZHAO Yan, GAO Shesheng, ZHANG Jing, et al. Robust predictive augmented unscented Kalman filter[J]. International Journal of Control Automation & Systems, 2014, 12(5): 996-1004. DOI: 10.1007/s12555-013-0048-2 |
 2017, Vol. 49
2017, Vol. 49


