带有翼面控制的航行体模型风洞试验显示,航行过程中机翼的翼梢涡和因襟翼打开导致翼面不连续而造成的涡系在近场的尾流中相互作用,这两个涡系是尾流的主要成分.此外还包括从主机翼短舱结合部脱落的涡、尾翼翼梢涡、翼身组合体涡等各涡系,这些强度和尺寸各异的涡系在近场中最终合并为两个对称的集中涡.由于风洞中均匀来流的整流作用,将这些低动量高涡量的流体通过对流作用快速合并在一起.在近场尾流中,由于相互的诱导运动,脱体涡系发生了短波失稳包括已知的椭圆失稳、合作失稳和其他形式的失稳,涡在近场的互诱导作用使得涡核心区域涡量略有减低,涡发生了翻转和扩散,涡系逐步趋向于合并.
相互诱导形成的涡系运动对尾流中最终形成的涡的尺寸和强度以及持续时间等均起着决定性作用,研究这些涡系的空间演化,可揭示尾迹的演化规律.通过文献归纳,按照涡雷诺数的大小将涡的合并可分为准二维层流合并和三维短波椭圆合并两种合并的形式.一般认为200 < ReΓ < 2 000时,两个涡发生层流合并,Paulo等[1]对层流阶段的二维共转涡对合并的雷诺数效应进行了数值和理论建模,指出增大雷诺数加速了涡的合并.Cerretelli等[2]通过试验和数值计算指出在一个寂静的背景流场中各自独立的一对共转涡的合并历经4个阶段:初始阶段是两个独立的涡的扩散增长,随后这两个涡相互诱导而绕着对方旋转,直至因为黏性扩散使得涡半径增加而发生合并.随着涡半径的持续增长,二涡进一步融合,由于涡量的扩散造成了无法区分互相旋转的两个涡的各自的边界,同时在原集中涡量的区域外部诱导了一个涡量循环的区域,从而形成了一个反对称的涡量分布,这加速对流合并;第2阶段是涡心互向运动,这种运动几乎不依赖于黏性,在这一阶段的后期反对称的涡量在对称化的过程中逐渐消失;第3阶段是通过扩散作用,二涡最终合并为一个轴对称的涡;最后一个阶段是合并后的涡尺寸逐渐增长直至黏性耗散.
针对高雷诺数情况下的飞行器三维空间绕流,为了抽象出合理的尾涡结构的理论和实验模型,Fabre等[3]推导两个平行的有涡核结构的无限长涡丝的诱导失稳, 并解释了飞行器远场尾迹中经常观察的失稳形式.Crouch[4]建立了二涡对的共转失稳模型,而Spalart[5]应用对转二涡对描述飞机尾流的优化扰动,用最优扰动分析来描述实际观察到的飞机尾涡构型是内襟翼的脱落涡和平尾翼梢涡的失稳可能性.Leweke等[6]研究了对转涡对的三维短波失稳,失稳波长约为涡核的尺寸,通过细致的流场可视化和测速揭示了失稳涡对的空间结构.文献[6]发现了各涡的扰动演化遵守一个运动匹配条件,每一个涡的耦合失稳被称为合作失稳.Crow[7]构造了两对对转涡对空间演化,利用文献[4]的对转涡模型描述飞机远场尾涡的失稳.
近场生成的涡系不满足文献[7]关于柱涡间距离远大于涡的半径的假设,也不满足长波合作失稳的基本假设,也不是初始小扰动造成涡系失稳,近场涡系存在于机翼脱体的自由剪切流中,连通集中涡的剪切层起到了加速涡系合并的作用.航行器的尾流中存在大量的共转涡合并的现象,尾涡合并不仅是远场尾迹的形成的主要内容,而且与近场涡致阻力紧密相关,航行器布局设计应与涡致阻力之间通过涡合并动力学过程建立桥梁;远场中存在的合作失稳则对飞机的尾流尺度效应产生影响,决定了机场的起降容积率.深入研究涡在近场的合并,将有助于揭示尾迹的形成机制和规模.Breitsamter[8]对飞机模型尾流风洞试验进行了系统总结,指出飞机机翼的翼面不连续处的脱落尾涡在近场中以共转和对转合并是尾流结构形成的主要机制.Delbende等[9]扩展到三维螺旋形涡的合并,指出螺旋形涡的自诱导作用对涡的合并起到了延迟作用.Laurent等[10]指出共转合并后的涡系不稳定性特征,Churchfield等[11]和Devenport等[12]对翼梢涡的合并进行了系统实验和数值分析给出了翼尖涡初生的细节.Bristol等[13]对平行涡系诱导合并过程进行了模拟.
不同于经典的二维情况下的共转涡合并,涡合并的三维效应显示了独特的三维涡拉伸,诱导共转和剪切变形失稳等独有的物理现象.调整舵面布局,例如调整内外襟翼的构型和布局,合理配比设计翼面积分布与后掠角、扭转角等构型参数,制造合理的尾流涡系近场分布,延缓各类涡系共转和对转合并,对制造有益于航行性能的诱导下洗流场起到至关重要的作用,本文针对翼梢和襟翼脱落的涡系在尾流中的诱导共转与合并运动特征,系统的描述尾流结构演化.
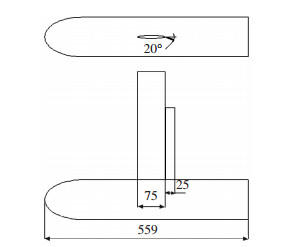
1 数值模型与验证 1.1 计算设置为研究绕流场中相邻的两个涡的相互诱导运动与合并,Bruin等[14-15]设计了如图 1所示的模型,并进行了系统的风洞试验,测试了机翼的翼梢脱体涡与襟翼翼梢发放的涡在尾流中的相互作用的尾流速度场.试验的弦长雷诺数为2.98×106,测量距机翼尾缘10倍的机翼展长至30倍的机翼展长范围内若干横截面的速度分布.可供开展数值模拟的验证对比,试验模型的详细尺寸见表 1.
|
图 1 实验模型尺寸 Figure 1 Dimension of experimental mode |
| 表 1 SWIM模型参数 Table 1 Dimensions of SWIM model |
计算采用有限体积法求解雷诺平均方程结合SST k-ω湍流模型与近壁面处理模型,近壁面区域网格加密满足给定来流速度条件下y+≈1,速度与压力的耦合采用PISO算法,采用二阶迎风对流格式离散动量方程,求解格式细节与离散数值处理方法在此不做详述.比照风洞试验,选取来流速度为60 m/s的常温空气作为计算介质,来流攻角为0°,远场边界采用速度入口,对应于风洞试验中的来流湍流度为2.5%,远场压力出口和对称面边界,壁面采用了无滑移边界条件.为获得更为详细的尾流结构,对尾流场的远场采用200倍的机翼展长作为扩展计算域,并对尾流区域做了网格加密.
除了用于验证风洞试验的算例之外,计算中省略了风洞试验中存在的支柱和导流罩,这些支撑结构对翼梢和襟翼后方的尾流流场造成的影响小,本文省略这些次要因素,网格无关性是通过涡核位置捕捉精度的比较来确定,最终选取网格为轴向×周向×展向=450×100×50,网格划分和边界设置如图 2所示.

|
图 2 网格划分与边界条件设置 Figure 2 Boundary condition and surface mesh |
本研究选取机翼展向距离导流罩0.15 m处的截面压力测试数据与数值计算进行比较,压力曲线分布比较如图 3所示.带有襟翼的机翼增升效果显著,机翼尾缘没有显著的压力下降.

|
图 3 y/b1=0.5截面处压力系数试验值与计算值比较 Figure 3 Pressure coefficients comparison from numerical simulation and experiment at y/b1=0.5 |
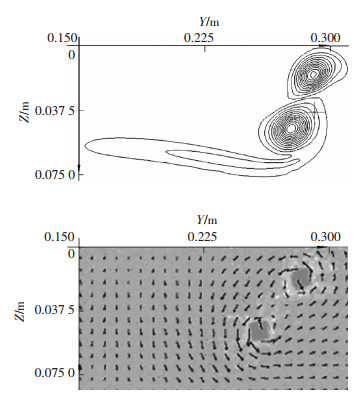
比较图 4、5可知,采用PIV试验获得的尾涡位置与形态与数值计算结果基本一致,集中涡量的核心区位置略有差别,数值模拟襟翼涡与翼梢涡的形态和互诱导运动与实验基本一致.本文建立的数值方法能够准确模拟襟翼与翼梢形成的尾涡流动结构的演化.数值方法可获得二涡在尾流中出现的合并现象,并描述近场涡系共转涡对的合并造成涡的尺寸在尾流中迅速的扩大等三维诱导运动现象.

|
图 4 风洞试验测得的x/b1=1.25处尾涡系位置与数值结果比较 Figure 4 Vortices position comparison from numerical simulation wind tunnel experiment at x/b1=1.25 |
|
图 5 风洞试验测得x/b1=5.0处尾涡系位置与数值结果比较 Figure 5 Vortices position comparison from numerical simulation wind tunnel experiment at x/b1=5.0 |
在该阶段中翼梢涡与襟翼涡各自具有独立的涡系结构,可利用经典的兰金涡理论模型描述涡核结构,随着涡脱体后,受横流效应和机翼脱体的自由剪切层影响,涡呈现轴对称结构,涡的尺寸增长但涡量衰减.随后两个柱状涡受到互相的诱导而翻转,涡核轨迹形成了螺旋线,柱状集中涡由于互诱导而逐渐失去轴对称的特征,两个涡逐渐靠近.
2.2 共转涡的合并20 < x/Δ < 50由于二涡间存在机翼尾流的自由剪切层,该剪切层起到了连接二涡的作用,剪切层卷起后,二涡的涡核靠近,涡首先出现椭圆失稳变形,涡相互靠近,直至不能区分两个涡的边界,无法辨识出涡核的各自位置.
2.3 结果涡的轴对称化阶段50 < x/Δ合并的涡在尾流中进一步轴对称化,在轴对称化的过程中,结果涡的尺寸保持一定.涡的结构逐步由椭圆形过渡到具有近似兰金涡速度剖面的形状.随着尾涡在流场中的扩散,尾涡的尺寸达到极限尺寸,涡量的峰值缓慢衰减下降.
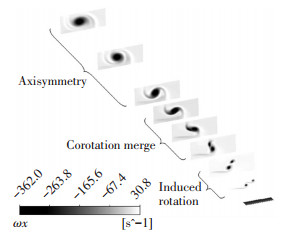
可见上述合并的动力学过程具有自相似的特征,即具有相似结构的襟翼涡和翼梢涡合并后的结果涡也具有与子涡相似的结构特征.尾流结构划分如图 6所示.
|
图 6 带有襟翼的机翼尾涡流场划分 Figure 6 Tailing vortices dividing of flapped wing wake |
在第1个阶段由于二涡的独立性强,涡间相互作用以互诱导的翻转运动为主,那么涡系可利用下述涡辨识方法得到涡核心运动轨迹.对于柱状涡而言,沿着下游发展的涡系轴向涡量在任意横截面的分布为
| $ {\mathit{\boldsymbol{\omega }}_x} = \frac{{\partial \mathit{\boldsymbol{w}}}}{{\partial y}} - \frac{{\partial \mathit{\boldsymbol{w}}}}{{\partial z}}. $ |
对应的环量为
| $ {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_x} = \int_{{z_1}}^{{z_2}} {\int_{{y_1}}^{{y_2}} {{\mathit{\boldsymbol{\omega }}_x}{\rm{d}}y{\rm{d}}z} } . $ |
单个涡的涡心位置为:
| $ \bar y = \frac{1}{\mathit{\Gamma }}\int_{{z_1}}^{{z_2}} {\int_{{y_1}}^0 { - y{\mathit{\boldsymbol{\omega }}_x}{\rm{d}}y{\rm{d}}z} } , $ |
| $ \bar z = \frac{1}{\mathit{\Gamma }}\int_{{z_1}}^{{z_2}} {\int_{{y_1}}^0 { - z{\mathit{\boldsymbol{\omega }}_x}{\rm{d}}y{\rm{d}}z} } . $ |
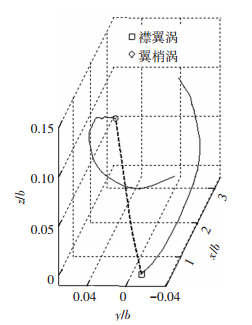
式中,积分上、下限以涡量的轴对称分布区域而定.那么涡系的核心轨迹通过对截取有限个尾流中近场截面得到如图 7所示的互诱导翻转运动.
|
图 7 尾流场中翼梢涡核与襟翼涡核的翻转运动轨迹 Figure 7 Trajectory of vortices rolling in the far field |
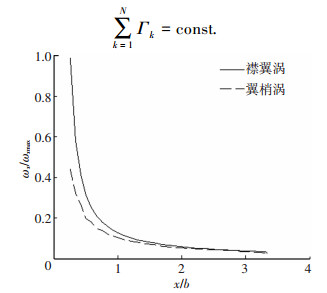
采用求解雷诺平均方程的方法求解流场.虽然实验中观察到的涡在x/b1>10之后仍能存在高涡量的集中涡,但是由于过分数值耗散,本文中给出的量纲-化的涡量耗散较试验显著,图 8显示了数值模拟给出的涡量在尾流中的耗散和扩散.在合并之前的阶段,设定襟翼涡涡强度Γ1和机翼的涡强度Γ2,根据数值计算得到涡在近场运动的轨迹,忽略黏性耗散作用,根据涡管强度保持定理,在近场认为涡系的总的涡强度保持不变,那么有
|
图 8 襟翼涡与翼梢涡涡量衰减 (U∞=60 m/s) Figure 8 Damping of flap vortex and tip vortex (U∞=60 m/s) |
| $ \sum\limits_{k = 1}^N {{\mathit{\Gamma }_k}={\rm{const}}} . $ |
不考虑涡系的三维诱导作用造成的环量衰减,以平面涡系运动来近似模拟二涡的互诱导翻转运动.涡系中的第m个涡受其他涡诱导产生的复速度为
| $ \frac{{{\rm{d}}{{\bar z}_m}}}{{{\rm{d}}t}} = \sum\limits_{k = 1,k \ne m}^N {\frac{{{\mathit{\Gamma }_k}}}{{2\pi i}}\frac{1}{{z - {z_k}}}} , $ |
两边同乘以Γm,两边对m求和得到:
| $ \sum\limits_{{\rm{m}} = 1}^n {{\mathit{\Gamma }_m}\frac{{{\rm{d}}{{\bar z}_m}}}{{{\rm{d}}t}}} = 0, $ |
积分得到:
| $ \sum\limits_{{\rm{m}} = 1}^n {{\mathit{\Gamma }_m}{{\bar z}_m}} = {\rm{const,}} $ |
那么复数的实部和虚部分别为常数,可写出点涡系的重心位置为:
| $ {y_c} = \frac{{\sum\limits_{{\rm{m}} = 1}^n {{\mathit{\Gamma }_m}{y_m}} }}{{\sum\limits_{{\rm{m}} = 1}^n {{\mathit{\Gamma }_m}} }},{z_c} = \frac{{\sum\limits_{{\rm{m}} = 1}^n {{\mathit{\Gamma }_m}{z_m}} }}{{\sum\limits_{{\rm{m}} = 1}^n {{\mathit{\Gamma }_m}} }}. $ |
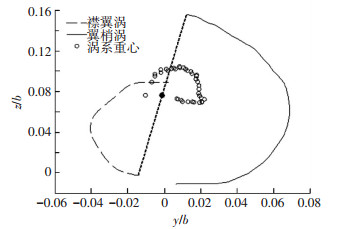
实际在尾流中不同的位置,处于机翼脱体的剪切层中的集中涡量迅速的耗散.故每一个流场剖面内的重心位置均不同,重心位置分布如图 9所示.重心位置的变化反映出二涡共转诱导运动使涡处于不稳定状态,相互靠近逐渐诱导扩散的特征.
|
图 9 襟翼涡与翼梢涡共转诱导运动的重心轨迹 Figure 9 Induced co-rotation centriod of flap vortex and tip vortex |
同一个雷诺数下,采用涡间距量纲-化尾流场截面位置,可完整的描述尾涡合并的过程,改变襟翼翼梢与机翼翼梢的间距Δ对二涡合并的影响,通过间距调整使二涡合并的过程得到改变,扩展计算了襟翼翼梢与机翼翼梢不同间距情况下的二涡合并的情况,图 10显示了采用x/Δ作为量纲-化参数描述不同涡间距的二涡合并的过程,上述划分适用于描述尾涡合并的3个阶段.如图 10所示,缩短襟翼翼梢与机翼翼梢的间距,加速翼梢涡与襟翼涡的合并过程,使得合并涡的尺寸得到快速的增长并迅速达到极限尺寸.

|
图 10 不同翼梢间距的近场尾涡合并 Figure 10 Trailing vortices merging of different interval distance |
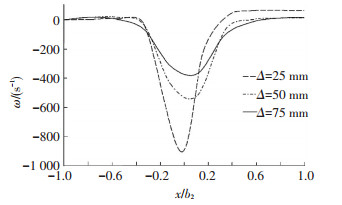
如图 11在x/Δ=60处的尾流场截面处,涡已经处于合并后的轴对称化阶段,对于柱状轴对称涡而言,结果涡的尺寸并不随着涡间距减小而显著的增加,但涡量的峰值具有较大差异.表明量纲一的参数x/Δ无法描述轴对称化后的涡量扩散的过程.
|
图 11 x/Δ=60处合并后涡的涡量剖面 Figure 11 Resulting vorticity profile at far field x/Δ=60 |
随着来流速度的增加,尾流中集中涡的强度急剧的增加,合并过程必然随着涡强度增加而产生差别.对于全尺度的实际流动而言,涡的耗散过程是极为缓慢的,但是对于模型尺度的涡而言,涡的耗散相对较快.本文改变翼的展长对比发现涡的合并依赖于涡间距离和涡的初始尺寸与形态.对于较低的雷诺数而言,集中涡总是尺寸快速增长,因此涡总会在近场首先合并.随着雷诺数增加,涡的合并过程被推迟到更大的x/Δ值,因此近场的涡互诱导运动现象与低雷诺数略有不同,即使弦长雷诺数大于105后,尾流中涡的合并过程继续随着雷诺数的增长而被推迟.本文选取对应于风洞试验的标准算例对应风速的0.5倍和2.0倍进行模拟,进而分析涡系运动轨迹与合并雷诺数效应.图 12、13显示在同一个截面位置不同量级的雷诺数情况下两个涡的合并状态.对比图 12、13可知随着涡的强度增加涡量的扩散程度减低,合并被推迟,独立涡量的空间互诱导运动得到延长.

|
图 12 Δ=75 mm,x/Δ=20处轴向涡量等值线云图 Figure 12 Axial vorticity contour at Δ=75 mm, x/Δ=20 |

|
图 13 Δ=25 mm,x/Δ=20处轴向涡量等值线云图 Figure 13 Axial vorticity contour at Δ=25 mm, x/Δ=20 |
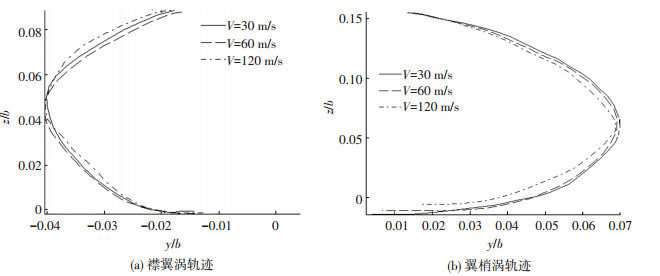
在与风洞实验对应的数值算例中发现,由于襟翼涡的涡量集中,初始强度约是翼梢涡的2倍,那么翼梢涡受到襟翼涡诱导而发生翻转卷曲运动,如图 14所示随着雷诺数的增加而逐渐增强,涡的卷曲效应增加,由图 14可知翼梢涡翻转轨迹曲率随雷诺数而增大.在图 14中显示二涡强度比在流向趋于接近的同时,二涡的诱导作用形成的轨迹趋于一致.
|
图 14 襟翼涡与翼梢涡近场轨迹 (x/Δ < 20) Figure 14 Rolling trajectories of flap vortex and tip vortex (x/Δ < 20) |
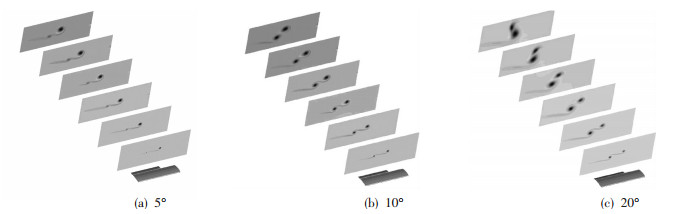
通过改变襟翼角度,使得二涡的强度比在初始生成时减小,分析二涡强度变化对合并过程的影响.涡间诱导效应决定于涡强度的大小和二者强度之比Γ1/Γ2.在上述验证模型算例的基础上调整襟翼角度分别为20°、10°、5°,随着襟翼角的增加,襟翼涡的强度不断的增大,襟翼涡对翼梢涡的诱导作用变得越来越显著,结果涡的尺寸有所增长.襟翼角为5°时,处于自由剪切尾流中的襟翼涡受到机翼的翼梢涡的拉伸而变形,形成快速的椭圆失稳,逐渐拉伸成为剪切层被翼梢涡卷起,最终形成自由剪切层与机翼翼梢涡合并,翼梢涡并不发生翻转运动.随着襟翼角度的增加,至10°时,襟翼涡的强度增大,襟翼涡与机翼翼梢涡的互诱导运动增强,翼梢涡出现了翻转运动,襟翼涡与翼梢涡合并后的涡尺寸显著的增大.在如图 15所示的尾流云图可观察到襟翼20°时二涡呈现了互诱导翻转运动.
|
图 15 尾流中涡量分布云图对比 (Δ=100 mm,截面位置x/Δ=2.5至15间隔2.5) Figure 15 Comparison of vorticity contours (Δ=100 mm, from x/Δ=2.5 to 15 of interval 2.5) |
1) 采用涡间距值进行量纲-化,可划分含襟翼涡的翼梢尾流结构,根据运动特征可划分为诱导共转阶段、共转涡的合并、结果涡的轴对称化等3个主要阶段.但在对襟翼涡与翼梢涡的合并过程中未观察到二涡互诱导翻转运动轨迹超过180°的情况,说明襟翼涡系与翼梢涡系的三维空间拉伸失稳存在极限.并且在同一个襟翼角和雷诺数下,虽然襟翼涡和翼梢涡的间距不同,但合并之后的结果涡具有相近的尺寸和形态.
2) 襟翼涡的强度远小于翼梢涡的强度时,在近场襟翼涡被拉伸变形并被翼梢涡卷起,而翼梢涡的运动轨迹并未受到襟翼涡的诱导运动,随着襟翼角度的增加,襟翼涡强度增大,二涡形成了相互诱导运动与共转合并.
3) 当Re<106时,随着Re的增加,可观察到尾流中一定程度的Re效应.随着Re的增大,涡的强度增加,涡量的扩散程度减低,合并过程被推迟,空间诱导运动得到延长,Re效应减低.
| [1] | PAULO J, FERREIRA S, PEREIRA J. Reynolds number dependence of two-dimensional laminar co-rotating vortex merging[J]. Theoretical and Computational Fluid Dynamics, 2005, 19(1): 65-75. DOI: 10.1007/s00162-004-0154-0 |
| [2] | CERRETELLI C, WILLIAMSON C. The physical mechanism for vortex merging[J]. Journal of Fluid Mechanics, 2003, 475(1): 44-77. DOI: 10.1017/S0022112002002847 |
| [3] | FABRE D, JACQUIN L, LOOF A. Optimal perturbations in a four-vortex aircraft wake in counter-rotating configuration[J]. Journal of Fluid Mechanics, 2002, 451(1): 319-328. |
| [4] | CROUCH J D. Instability and transient growth for two trailing-vortex pairs[J]. Journal of Fluid Mechanics, 1997, 350(1): 311-330. |
| [5] | SPALART R. Airplane trailing vortices[J]. Annual Review of Fluid Mechanics, 1998, 30: 107-138. DOI: 10.1146/annurev.fluid.30.1.107 |
| [6] | LEWEKE T, WILLIAMSON C H K. Cooperative elliptic instability of a vortex pair[J]. Journal of Fluid Mechanics, 1998, 360(1): 85-119. |
| [7] | CROW S. Stability theory for a pair of trailing vortices[J]. AIAA Journal, 1970, 8(12): 2172-2179. DOI: 10.2514/3.6083 |
| [8] | BREITSAMTER C. Wake vortex characteristics of transport aircraft[J]. Progress in Aerospace Sciences, 2011, 47(2): 89-134. DOI: 10.1016/j.paerosci.2010.09.002 |
| [9] | DELBENDE I, PITON B, ROSSI M. Merging of two helical vortices[J]. European Journal of Mechanics-B/Fluids, 2015, 49(2): 363-372. DOI: 10.1016/j.euromechflu.2014.04.005 |
| [10] | LAURENT J, DAVID F, DENIS S, et al. Unsteadiness, instability and turbulence in trailing vortices[J]. Comptes Rendus Physique, 2005, 6(5): 399-414. DOI: 10.1016/j.crhy.2005.05.007 |
| [11] | CHURCHFIELD J, BLAISDELL A. Numerical simulations of a wingtip vortex in the near field[J]. Journal of Aircraft, 2012, 46(1): 230-243. DOI: 10.2514/1.38086 |
| [12] | DEVENPORT J, RIFE C, LIAPIS I. The structure and development of a wing-tip vortex[J]. Journal of Fluid Mechanics, 1996, 312(4): 67-106. DOI: 10.1017/S0022112096001929 |
| [13] | BRISTOL R L, ORTEGA J M, MARCUS P S. On cooperative instabilities of parallel vortex pairs[J]. Journal of Fluid Mechanics, 2004, 517(517): 331-358. DOI: 10.1017/S0022112004001016 |
| [14] | BRUIN A. Test report for wake survey tests behind SWIM model geometry in DNWLST and DNW-LLF wind tunnels: NLR-TR-2001-183[R]. Netherlands: DNW-LLF/ LST wind tunnels, 1999. |
| [15] | BRUIN A, Ganzevles F. Data analysis of wake survey tests behind SWIM model geometry in DNW-LST and DNW-LLF wind tunnels: NLR-TR-2001-201[R]. Netherlands: DNW-LLF/ LST wind tunnels, 2001. |
 2017, Vol. 49
2017, Vol. 49


