虽然Apollo飞船的制导方法已经成功地用于60年代的登月计划,但是随着科技发展,Apollo飞船的技术条件已经不能满足目前的需求.特别是对于大航程返回时,Apollo制导方法的误差达到了数百公里,并且Apollo的跳跃返回方式从未得到验证[1].新一代的飞船必须能够承载更多的成员或货物,在太空或月球停留更长的时间,能够实现任意时刻返回地球都降落在本土以及躲避恶劣天气状况,而且飞船必须能够重复使用.因此,对飞行器返回时的落点精度以及航程都提出更高的要求.探月飞船返回地球时的能量远高于近地返回再入,使得探月飞船和乘员必须承受更大的过载,导致再入走廊更为狭窄.另一方面,飞船必须能够覆盖非常大的航程范围 (约2 000~10 000 km),因此要求制导方法既能实现直接再入,又能实现跳跃再入;而且跳跃轨迹在跳跃段倾侧角偏转次数过多不仅无助于提高制导精度,还会消耗过多的能量,增大制导失败的风险.这些因素给制导方法的设计带来了很大的挑战.
探月返回再入的数值预测校正制导方法主要分为两类:以Apollo制导方法为基础的部分数值预测校正和全程数值预测校正.部分数值预测校正制导方法充分利用Apollo制导方法的遗留成果,但是与全程数值预测校正制导方法相比仍然存在精度欠佳,鲁棒性不好的缺点[1-3].随着计算机技术的发展,全程数值预测校正制导方法也显现出了其鲁棒性高、精度好的优势.文献[4-5]提出了一种全程数值预测校正的制导方法,并且采用基于虚拟落点的方法补偿了跳跃轨迹在真空飞行时缺乏控制能力而导致的横程偏差.文献[6]提出一种基于解析常值气动过载计算与数值预测校正技术相结合的融合再入制导方案,当气动过载到达约束值时以使得气动过载导数为零的倾侧角飞行,能够对气动过载进行一定程度的抑制.文献[7]提出了一种通过搜索合适的倾侧角偏转能量点来消除横程误差,通过调节升阻比在垂直方向的分量来调节纵程大小的制导方法,计算量较大.文献[8]则着重研究了跳跃再入过程中的过载抑制方法,并从理论上进行了阐释.文献[9]提出了基于全系数自适应校正的预测制导方案,提高了制导方法对再入初始条件散布的适应性,获得了比现有制导方法更高的精度.
虽然文献[4-5]解决了跳跃轨迹全程数值预测校正方法中真空飞行段缺少控制能力而带来的横程误差过大的问题,但是跳跃段大气密度稀薄,侧向阻尼小,飞行器容易频繁触及侧向走廊边界,导致倾侧角频繁偏转,这样频繁的偏转不仅没有必要而且需要消耗额外的能量.文献[10]通过设计一个拼接的侧向再入走廊,减少了跳跃轨迹再入过程中的倾侧角偏转次数,但是走廊的设计繁琐,需要对大量的参数进行试探与调整,任务适应性较差.另外文献[4-5, 10]也没有考虑再入过程中的过载约束.文献[6]中的制导方法显然存在开环飞行段,导致鲁棒性不好,制导精度不高.文献[8]的抑制过载方法对于航程较小的直接再入并不适用.本文将针对上述探月返回再入制导方法的不足,通过对跳跃段与末段分别设计不同的倾侧角反转策略,减少倾侧角的反转次数,并且保证第2次再入大气时的横程在制导方法所能修正的范围内.同时采用在开普勒段以大倾侧角飞行以及在末段采用阻力加速度反馈的方法减小过载, 提出一种倾侧角反转次数合理、能够在跳跃再入和直接再入条件下实现过载抑制的全程数值预测校正再入制导方法.
1 动力学方程与再入过程 1.1 动力学方程假设地球为均匀圆球体,考虑地球自转,则再入动力学方程为[4, 8]:
| $ \dot r = V\sin \gamma , $ | (1) |
| $ \dot \theta = \frac{{V\cos \gamma \sin \psi }}{{r\cos \varphi }}, $ | (2) |
| $ \dot \varphi = \frac{{V\cos \gamma \cos \psi }}{r}, $ | (3) |
| $ \dot V = - D - \left( {\frac{{\sin \gamma }}{{{r^2}}}} \right) + {C_V}, $ | (4) |
| $ \dot \gamma = \frac{1}{V}\left[ {L\cos \sigma + \left( {{V^2} - \frac{1}{r}} \right)\left( {\frac{{\cos \gamma }}{r}} \right) + {C_\gamma }} \right], $ | (5) |
| $ \dot \psi = \frac{1}{V}\left[ {\frac{{L\sin \sigma }}{{\cos \gamma }} + \frac{{{V^2}}}{r}\cos \gamma \sin \psi \tan \varphi + {C_\psi }} \right]. $ | (6) |
其中:CV、Cγ、Cψ分别为地球自转引起的附加项,分别为
| $ \begin{array}{l} {C_V} = {\mathit{\Omega }^2}r\cos \varphi \left( {\sin \gamma \cos \varphi - \cos \gamma \sin \varphi \cos \psi } \right),\\ {C_\gamma } = 2\mathit{\Omega }V\cos \varphi \sin \psi + \\ \;\;\;\;\;\;\;{\mathit{\Omega }^2}r\cos \varphi \left( {\cos \gamma \cos \varphi + sin\gamma \cos \psi \sin \varphi } \right),\\ {C_\psi } = - 2\mathit{\Omega }V\left( {\tan \gamma \cos \psi \cos \varphi - \sin \varphi } \right) + \\ \;\;\;\;\;\;\;\;\frac{{{\mathit{\Omega }^2}r}}{{\cos \gamma }}\sin \psi \sin \varphi \cos \varphi . \end{array} $ |
式中:r为地心距;θ、φ分别为经度、纬度;V为飞行器相对于地球的速度;γ、ψ分别为航迹角、航向角 (参考方向为正北方向,顺时针为正);L、D分别为以g0(g0=9.81 m/s2) 为单位的升、阻力加速度;σ为倾侧角;Ω为地球自转角速度.为提高计算精度,减小舍入误差,式中各个量均进行了量纲一化,使得各个量均处于相近的数量级,其中地心距用地球赤道半径R0=6 378 136.3 m量纲一化;时间用
由于飞行时间并不是需要特别考虑的因素,为便于后续倾侧角幅值剖面的设计,定义能量参数为
| $ e = \frac{1}{r} - \frac{{{V^2}}}{2}, $ | (7) |
对式 (7) 关于量纲一的时间τ进行求导,同时忽略地球自转,可以得到[8, 11]:
| $ \frac{{{\rm{d}}e}}{{{\rm{d}}\tau }} = DV \ge 0, $ |
因此,当飞船处于真空段时,e保持不变,处于大气层内时e随时间增长而增大.
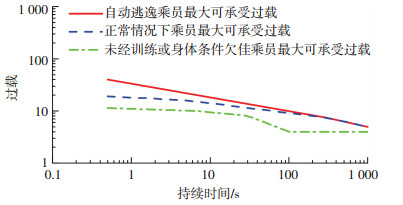
1.2 再入轨迹约束对于飞船构型的飞行器而言,没有气动舵面,因此不存在因动压过大而导致舵机能力饱和以及蒙皮翁鸣和壁板颤振的问题,因此不用考虑动压约束.热流是另一个影响飞行走廊的因素,然而对于飞船而言,它的烧蚀热防护材料具有非常高的热流容差,月球返回再入时的热流峰值通常只接近烧蚀材料防护极限的1/2[12],实际中热流约束也不予考虑.过大的过载会破坏飞行器的结构,威胁乘员的生命安全.结构强度可以通过合理的设计满足要求,但是乘员对过载的耐受能力有限,必须通过减载措施对乘员承受的过载进行抑制.乘员对不同大小的过载所能承受的时间是不同的,过载愈大能够承受的时间愈短,反之亦然.NASA对此提出了一些准则,给出了一些条件下可接受的过载关于持续时间的函数,若违反过载约束,可能导致乘员的伤亡[13],其约束如图 1所示.本文以此作为过载抑制的参考标准.
|
图 1 不同条件下乘员可承受的最大过载约束 Figure 1 Over load constraints for the crew in different conditions |
再入轨迹的终端约束为剩余航程、高度以及速度约束,其中高度与速度约束可以合并为终端能量约束,因此终端约束可以写为:
| $ e\left( {{t_{\rm{f}}}} \right) = {e_{\rm{f}}},s\left( {{e_{\rm{f}}}} \right) = 0, $ | (8) |
式中s为剩余航程,定义为
| $ \dot s = - \frac{{V\cos \gamma }}{r} $ |
倾侧角幅值剖面一般设计为常值或分段线性函数,分段线性倾侧角幅值剖面较常值倾侧角幅值剖面具有更好的鲁棒性[11].本文期望倾侧角的幅值变化发生在控制能力较强的飞行阶段,而在控制能力较弱的飞行阶段尽量避免倾侧角的变化,以节省能量.文献[4-5, 8]将倾侧角幅值剖面设计为剩余航程的分段线性函数,但航程的变化并不能反映控制能力的变化,这样设计出的倾侧角幅值剖面从节省燃料的角度来讲是不合理的.另外,对于探月返回轨迹而言,其航程变化范围非常大,以航程作为倾侧角幅值剖面的自变量将导致不同再入条件下倾侧角幅值剖面发生很大变化,需要针对不同的再入条件对倾侧角幅值剖面进行重新设计.然而,再入时的能量变化却是相对稳定的,而且能量的大小也能一定程度上反映控制能力的变化,因此适合作为倾侧角幅值剖面的自变量.定义倾侧角幅值剖面为
| $ \left| \sigma \right| = \left| {{\sigma _0}} \right| + \frac{{\left| {{\sigma _{\rm{f}}}} \right| - \left| {{\sigma _0}} \right|}}{{{e_{\rm{f}}} - {e_0}}}\left( {e - {e_0}} \right). $ | (9) |
式中:e0为当前时刻的能量,e∈[e0, ef];|σ0|为当前倾侧角幅值;|σf|为末端倾侧角幅值,取60°~70°较为合适,过小会导致制导方法缺乏纵向裕度,过大会导致缺乏横向裕度,都会影响鲁棒性.
2.2 跳跃段制导算法设计本文将跳跃段定义为从再入点到第2次进入大气层的飞行阶段,为便于制导算法的设计,认为当剩余航程小于2 000 km时,跳跃段结束[4].这一阶段的显著特点是存在真空飞行段.在真空中飞行时,由于缺乏控制力,倾侧角的偏转并不能消除横程误差,导致第2次再入时的横程偏差超过飞行器所能修正的范围,制导误差急剧增大,而且由于倾侧角的偏转依赖于设计好的倾侧角幅值边界,使得跳跃段的倾侧角偏转次数过多.
本文采用跳跃段倾侧角只进行一次反转,通过搜索反转点的能量值的方法保证第2次进入大气时具有较小的横程,并且大大降低反转次数.定义纵程与横程如图 2所示,即:

|
图 2 跳跃段横程与纵程定义 Figure 2 Definition of the cross range and down range in the skip phase |
| $ \begin{array}{l} CR = \arcsin \left( {\sin {s_{{\rm{arc}}}}\sin \Delta \psi } \right),\\ DR = \arccos \left( {\cos {s_{{\rm{arc}}}}/\cos \left( {CR} \right)} \right). \end{array} $ |
式中:CR为横程弧长;DR为纵程弧长;sarc为再入点到落点之间的大圆弧长;Δψ为包含再入点与落点的大圆弧和包含再入点与着陆场的大圆弧之间的夹角.
由于跳跃段之后还有末段制导保证制导精度,所以跳跃段的制导精度可以适当放宽,只需预测落点距着陆场的距离在一定范围内即可.即:
| $ \left| {DR - D{R_0}} \right| \le {\delta _1},\left| {CR} \right| \le {\delta _2}. $ |
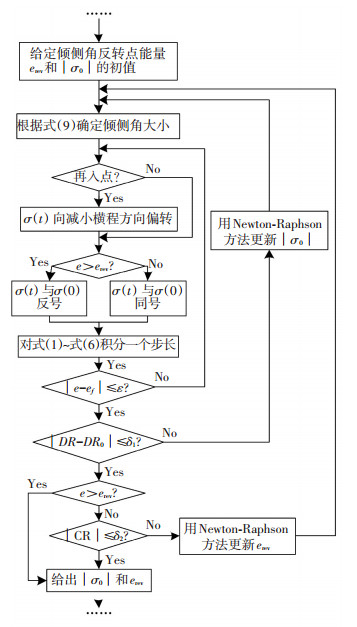
式中:DR0为再入点到着陆场的大圆弧长,兼顾计算精度和计算速度;δ1、δ2分别取1×10-6和2.5×10-3.显然,跳跃段的制导是一个二维根的搜索问题.但是二维根的搜索计算量大,收敛性差,因此本文采用两层搜索的方法将二维搜索转化为一维搜索,流程如图 3所示.
|
图 3 跳跃段一个制导周期的制导流程 Figure 3 Flow chart of the guidance scheme for the skip phase in one guidance cycle |
根据图 3给出的跳跃段一个制导周期内的制导指令的生成方法,不断重复上述步骤,直至跳跃段制导结束,形成闭环制导.但是,当飞船在接近真空环境飞行时几乎没有控制能力,倾侧角无法改变飞行轨迹,此时的制导是没有必要的,而且倾侧角的偏转也会导致能量的不必要消耗.因此,当阻力加速度小于0.2g0时停止制导,倾侧角保持常值,直到阻力加速度大于0.15g0时恢复制导[1, 4].
2.3 末段制导算法设计当剩余航程小于2 000 km,并且阻力加速度大于0.15g0时,末段制导开始.末段制导的精度决定了整个再入制导的精度,采用倾侧角只偏转一次的策略会带来较大的误差.因此末段制导采用纵向制导确定倾侧角幅值,当横程超过给定的边界时倾侧角反号的制导策略.
2.3.1 纵向制导算法纵向制导的目的是消除纵程误差.以σ为纵向运动的控制量,对纵向运动方程进行数值积分,当能量到达ef停止积分,此时的剩余航程为sf,即为预测剩余航程.由式 (9) 可知,sf为|σ0|的函数,即
| $ {s_{\rm{f}}} = {s_{\rm{f}}}\left( {\left| {{\sigma _0}} \right|} \right), $ |
通过数值方法对|σ0|进行调整,使得预测剩余航程满足约束式 (8) 即可得到一条可行的飞行轨迹和对应的倾侧角幅值剖面为
| $ {s_{\rm{f}}}\left( {\left| {{\sigma _0}} \right|} \right) = 0. $ | (10) |
结合侧向制导 (确定倾侧角符号),飞船以得到的倾侧角飞行,到达下一制导周期时再以当前状态作为初始状态重复上述过程,从而形成闭环制导.
显然,方程 (10) 的求解是一元方程的求根问题.但是,如果方程的解不存在,当求解过程结束时|σ0|将是一个不确定的值,从而带来不必要的制导误差甚至导致制导失败.当方程 (10) 的根存在时,它的根等价于式 (11) 所示的极小值问题的极值点;而当前者无解时,后者的极小值点仍然存在,而且具有明显的物理意义-使轨迹终点距着陆点的距离最小.
| $ \min \left( {s_{\rm{f}}^2\left( {\left| {{\sigma _0}} \right|} \right)} \right). $ | (11) |
因此,本文采用求解式 (11) 所示的极小值问题的方法求解|σ0|的值.由式 (9) 可知,当前倾侧角的大小|σ|即为|σ0|.
2.3.2 侧向制导算法侧向制导的主要任务是确定倾侧角的符号,将再入过程中的横程约束在一定范围内,并逐步减小横程的大小,确保落点的精度并控制倾侧角偏转的次数.采用与Apollo制导类似的侧向边界为
| $ \bar Z = {k_1}V + {k_2}, $ |
式中,k1, k2分别为常量.重新定义横程为
| $ Z = \arcsin \left( {\sin {s_{{\rm{arc}}}}\sin \Delta {\psi _V}} \right). $ |
重新定义的横程的几何关系如图 4所示.ΔψV为当前速度矢量与包含当前位置和着陆场的大圆弧之间的夹角.当Z的大小超过Z时,倾侧角立即开始向相反方向偏转,随着侧向边界Z的不断收缩,当接近着陆点时横程Z就被约束在很小的范围内.

|
图 4 末段横程与纵程定义 Figure 4 Definition of the cross range and down range in the final phase |
由于跳跃段制导的横程定义与末段制导的横程定义不同,为了避免在跳跃段制导结束时|Z|的值过大,对跳跃段制导过程中得到的erev进行修正:
| $ {{\hat e}_{{\rm{rev}}}} = {e_{{\rm{rev}}}} - k\left| Z \right|, $ |
即|Z|的值越大,倾侧角越提前偏转,避免长时间向同一侧飞行导致|Z|过大,k为比例系数,取值0.85.
虽然纵向制导与横向制导是分开进行描述的,但是本文制导方法没有采用传统的纵向制导和横向制导解耦的方法,而是保留了它们的耦合特性.耦合制导将横向制导包含在纵向制导的迭代过程中,提高了制导的精度.特别是对处于飞船可达域边界附近的着陆点,解耦制导可能导致任务失败.
3 过载抑制对于高升阻比飞行器,可以通过准平衡滑翔条件将过载约束转化为对控制量的约束,从而将过载限制在约束范围内[14-16].但是对于小升阻比飞行器,飞行过程并不满足准平衡滑翔条件,无法利用准平衡滑翔条件将过载约束转化为对控制量的约束.
文献[11]研究了近地轨道再入的小升阻比飞行器的过载抑制方法,但是其过载抑制能力有限.文献[8]将文献[11]的方法应用于探月返回跳跃轨迹的过载抑制,给出了过载抑制的数学原理.本文在跳跃段利用同样的策略进行过载的抑制.但是,对于气动力影响较大的非开普勒轨迹,文献[8, 11]的过载抑制方法不再适用,因此本文提出一种能够在气动力影响较大的飞行阶段进行过载抑制的方法.
假设再入过程中最大过载约束为nmax,则最大阻力加速度约束为
| $ {D_{\max }} = \frac{{{n_{\max }}}}{{\sqrt {1 + {{\left( {\frac{{{C_{\rm{L}}}}}{{{C_{\rm{D}}}}}} \right)}^2}} }}. $ |
为使过载小于约束值,或者使过载在约束值的附近,可以用阻力加速度对式 (9) 得到的倾侧角幅值进行反馈修正,使得飞行的最大阻力加速度不超过Dmax为
| $ \cos {\sigma _{{\rm{cmd}}}} = \cos \sigma - {K_1}\left( {{D_r} - D} \right) - {K_2}\left( {{{\dot D}_r} - \dot D} \right) $ | (12) |
式中:K1、K2分别为增益系数;Dr、
| $ \begin{array}{l} {D_r} = \left\{ \begin{array}{l} D,D + \dot D\delta t < {D_{\max }};\\ {D_{\max }},D + \dot D\delta t \ge {D_{\max }}. \end{array} \right.\\ {{\dot D}_r} = \min \left\{ {\dot D,{{\dot D}_{\max }}} \right\}. \end{array} $ |
假设大气密度为高度的指数函数,即
| $ \rho = {\rho _0}{{\rm{e}}^{ - \beta h}}, $ |
则可以得到:
| $ \begin{array}{l} \dot D = \frac{{{g_0}{R_0}{S_{{\rm{ref}}}}}}{{2m{g_0}}}\left( { - \beta \rho {V^3}{C_{\rm{D}}}\sin \gamma - 2\rho VD - } \right.\\ \;\;\;\;\;\;\left. {\frac{{2\rho V\sin \gamma }}{{{r^2}}} + \rho {V^2}{C_{\rm{D}}}} \right),\\ {{\dot D}_{\max }} = - \frac{{{n_{\max }}\left( {\frac{{{C_{\rm{L}}}}}{{{C_{\rm{D}}}}}} \right)\left( {\frac{{{{\dot C}_{\rm{L}}}}}{{{C_{\rm{D}}}}} - \frac{{{C_{\rm{L}}}}}{{C_{\rm{D}}^2}}{C_{\rm{D}}}} \right)}}{{\left[ {{{\left( {\frac{{{C_{\rm{L}}}}}{{{C_{\rm{D}}}}}} \right)}^2} + 1} \right]\sqrt {{{\left( {\frac{{{C_{\rm{L}}}}}{{{C_{\rm{D}}}}}} \right)}^2} + 1} }}. \end{array} $ |
需要注意的是,式 (12) 并不是对纵向制导收敛后的倾侧角进行反馈补偿,而是在每一步迭代时采用将式 (9) 代入式 (12) 后的结果进行计算.
升阻力系数对飞行器的动力学特性有显著的影响,但飞行器的气动系数尚无法精确测量,而且现有的大气模型尚不能精确描述大气的随机扰动,导致气动力的标称值与真实值可能会产生较大的偏差.另外,所有影响飞船质心运动的扰动因素中,除了再入点状态偏差外,其他扰动因素只对飞船的升阻力加速度有较大影响.因此只需合理地对升阻力加速度进行滤波处理即可显著提高制导精度[4].
本文采用限定记忆滤波器对于升阻力加速度进行滤波处理[4]:
| $ {{\hat x}_n} = {{\hat x}_{n - 1}} + \left( {1 - \beta } \right)\left( {x_n^ * - {{\hat x}_{n - 1}}} \right). $ |
式中:xn*为当前测量值与标称值的比值;
本文采用的飞行器模型与Orion CEV类似[4],底部直径5 m,质量为8 382 kg,再入时以配平攻角飞行,配平攻角为Ma的函数.飞行过程中最大倾侧角速度和最大倾侧角加速度约束为[4, 11]:
| $ {\left| {\dot \sigma } \right|_{\max }} = 20\left( {^ \circ } \right)/s,\;\;\;\;{\left| \sigma \right|_{\max }} = 10\left( {^ \circ } \right)/{s^2}. $ |
为验证本文制导算法的正确性,对小航程、中航程和大航程的任务分别进行仿真验证.再入点及着陆点的状态参数见表 1.
| 表 1 不同任务下的再入点与着陆点状态 Table 1 Initial states and final states of testing missions |
进行扰动条件下的仿真可以评估制导算法的性能.再入点处的状态偏差与离轨制动时刻飞行器的位置和相对速度有关,除了再入点高度,其他初始点状态的扰动可以通过协方差矩阵求出,计算结果见表 2[4].
| 表 2 再入点状态与其他参数扰动分布 Table 2 Dispersions in the initial states and other parameters |
本文以USSA76大气模型作为基准大气模型进行仿真计算.对于大气扰动,最理想的模型是NASA的全球参考大气模型 (global reference atmospheric model, GRAM),但是GRAM模型难以获取.文献[4]中的部分仿真结果采用了所谓的大气扰动解析模型,但是该模型过于粗糙,不能反映大气密度扰动随高度增加而增大的特点.GRAM数据表明,当高度从0增长到101.498 4 km时,大气密度扰动的1-σ误差值近似从0.351 7%呈指数增长到15.365 9%,大气密度扰动可以近似拟合为[17]
| $ {\sigma _\rho }\left( h \right) = 0.003\;517\exp \left( {\frac{h}{{26.629\;766\;4}}} \right), $ |
式中,h为高度,km.为模拟大气密度误差扰动随高度变化的不确定性,本文提出如式 (13) 的大气密度扰动近似模型:
| $ \begin{array}{l} {\rho _{{\rm{true}}}} = {\rho _{{\rm{nom}}}}\left\{ {1 + \left\{ {{B_{{\rm{atm}}}} + \left[ {{M_1} + {M_2}\sin \left( {h{\omega _2}} \right)} \right] \times } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\left. {\sin \left( {h{\omega _1} + \lambda } \right)} \right\} \times {\sigma _\rho }\left( h \right)} \right\}. \end{array} $ | (13) |
式中:ρtrue为实际大气密度;ρnom为由USSA76大气模型计算得到的大气密度;Batm为常值偏差项,服从均匀分布,分布区间为[-1.0, +1.0];M1为低频扰动,服从均匀分布,分布区间为[-0.50, -0.25]∪[0.25, 0.50];M2为高频扰动,取值为M1的0~0.1倍; 其他参数及其分布详见文献[4],这里不再赘述.需要注意的是式 (13) 并不是对真实大气密度随机扰动的精确拟合,仅是为了测试算法的鲁棒性而引入的随机扰动[4].
4.3 标称再入标称再入在没有任何扰动和不确定性的条件下对本文提出的制导方法的正确性进行仿真验证.Orion CEV计划的着陆精度要求为5 km,但是考虑到降落伞打开后引起的飘移误差,认为当终点位置距离着陆点小于2.5 km时认为制导是完全成功的,当终点位置距离着陆点2.5 ~5.0 km时,认为制导50%成功,而当终点位置距离着陆点大于5.0 km时则认为制导失败[4].
图 5给出了任务1~任务4的剩余航程-高度剖面.可以看到航程越大,跳跃越明显,这是由于高度越高阻力加速度越小,为达到长航程的要求,飞船必须尽量在大气层外飞行.当航程小于一定值时,飞船不再跳出大气层.对于航程特别小的情况,需要尽快消耗能量,缩短航程,因此飞船将直接再入,轨迹不发生弹跳.图 6给出了各个任务对应的地面轨迹,不同航程的任务最终落点均在距着陆点2.5 km的范围内,满足制导精度要求.

|
图 5 不同任务的高度-剩余航程剖面 Figure 5 Altitude vs. range-to-go profiles for different missions |

|
图 6 不同任务的地面轨迹 Figure 6 Ground tracks for different missions |
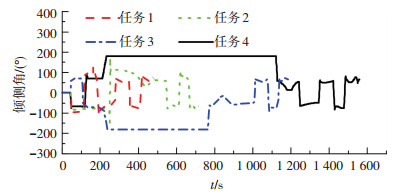
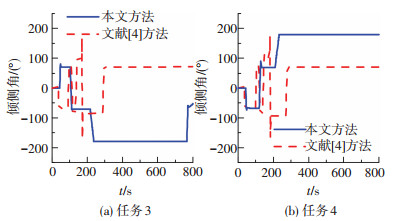
如图 7所示,航程较小的任务 (任务2、任务3) 的倾侧角并不存在常值飞行段,因此也无法利用长航程飞行时在高空段采用大倾侧角幅值飞行的方法进行过载的抑制,文献[8, 11]的方法不再适用.本文采用的针对小航程的过载抑制方法将在以后进行验证.对于长航程的情况,文献[4-5]的方法会引起跳跃段制导倾侧角偏转次数过于频繁,耗费不必要的能量,增加制导失败的风险.从图 8可以看出,在任务3和任务4的情况下,文献[4-5]的方法在跳跃段都会进行4次偏转,而本文方法只进行一次偏转.另外文献[4-5]的方法会随着航程的增大,跳跃段偏转次数也会随之增加,导致不必要的能量消耗, 而本文方法无论航程大小在跳跃段只进行1次倾侧角偏转.
|
图 7 不同任务的倾侧角剖面 Figure 7 Bank-angle profiles for different missions |
|
图 8 跳跃段倾侧角偏转次数对比 Figure 8 Comparison of the bank-angle reversal times in the skip phase |
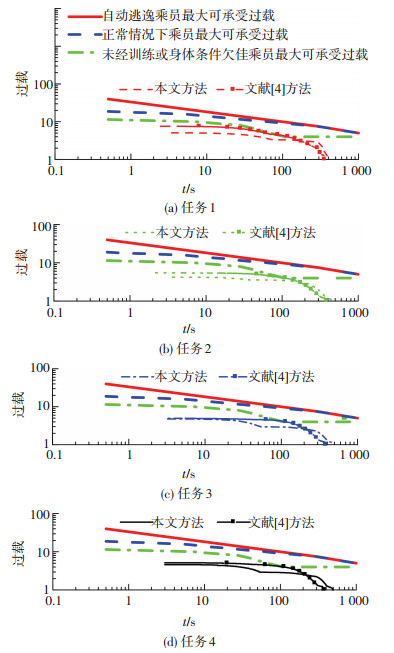
图 9给出了不同任务下过载的对比.任务1和任务2没有跳跃段飞行,不能用文献[8]的方法进行过载抑制,但是运用本文提出的方法依然达到了过载抑制的目的,所承受的最大过载值降低了1.5~2.5.任务3和任务4的过载曲线同样得到了非常大的改进,使得过载曲线远离约束曲线.大航程飞行时,过载的最大值本来就远离约束曲线,而过载持续作用时间成为了主要约束,从图 9中可以看到本文方法得到的大过载的作用时间远小于文献[4-5]方法得到的作用时间.本文方法很好地抑制了各种航程下的飞行过载,保证了乘员的安全,特别是对于身体状况出现意外的乘员尤其如此.
|
图 9 不同任务下过载约束对比 Figure 9 Comparison of the load constraints for different missions |
为更进一步测试本文提出的制导算法在各种大范围扰动条件下的性能,本节进行三自由度的蒙特卡洛仿真.再入点的状态偏差、大气扰动、质量偏差、气动力系数偏差等服从的分布以及分布参数在扰动模型已给出,共进行500次蒙特卡洛仿真.
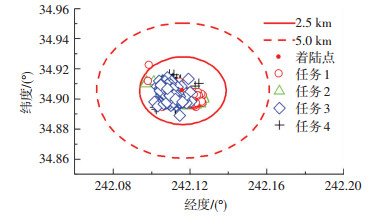
图 10给出了不同情况下最终落点的分布,除任务1有一个落点落在距着陆点2.5 km以外,其余所有落点均落在2.5 km的范围内.无论是短航程的任务1和任务2,还是长航程的任务3和任务4,落点都非常集中地分布在着陆点周围,表明了本文制导方法具有非常好的航程适应性和鲁棒性.
|
图 10 不同任务蒙特卡洛仿真落点分布 Figure 10 Final positions in the Monte Carlo simulations for different missions |
图 11描绘了不同任务下的过载剖面.可以看到,所有情况下的过载曲线都位于过载的最小约束曲线下方,特别是对于没有开普勒飞行段的任务1和任务2,它们的过载曲线仍然非常严格地满足了过载约束.文献[5-6]中采用了以常值倾侧角开环飞行的过载抑制策略,这无疑会影响到制导方法的鲁棒性与精度,而本文的过载抑制方法直接嵌入了闭环制导的每一制导周期,不会对制导方法的精度与鲁棒性产生影响,这一点可以从图 10得到验证.

|
图 11 不同任务蒙特卡洛仿真过载剖面 Figure 11 Load-constraint profiles in the Monte Carlo simulations for different missions |
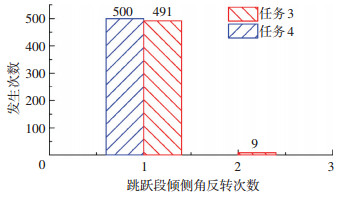
对蒙特卡洛仿真结果进行统计,图 12给出了跳跃段倾侧角反转次数的统计结果.即使在存在各种扰动的条件下,只有任务3在非常少的几种情况下跳跃段倾侧角反转了2次,其他情况都只反转1次,验证了本文减少倾侧角反转次数方法的有效性.
|
图 12 跳跃段倾侧角反转次数统计 Figure 12 Statistics of the bank-angle reversal times in the Monte Carlo simulations |
1) 本文提出了改进的数值预测校正制导方法,通过搜索倾侧角反转能量点的方法保证跳跃段的倾侧角只进行一次反转,同时保证第2次进入大气时的横程在允许范围内.
2) 结合开普勒段大倾侧角幅值飞行的策略,本文提出的基于阻力加速度反馈补偿的末段过载抑制策略,在不同航程、多种扰动的条件下均能够严格实现探月返回时的过载约束.
3) 大扰动条件下,本文提出的制导方法能够在2 000~10 000 km航程范围内实现落点误差小于2.5 km的制导精度,并且跳跃段倾侧角只有极少数情况出现2次反转,验证了本文方法的有效性和鲁棒性.
| [1] | BAIRSTOW S H. Reentry guidance with extended range capability for low L/D spacecraft[D]. Cambridge: Massachusetts Institute of Technology, 2006. |
| [2] | TIGGES M A, CRULL T, REA J, et al. Numerical Skip-Entry guidance[C]//Proceedings of the 29th Annual AAS Guidance and Control Conference. Breckenridge. Colorado: AAS, 2006: 1-21. |
| [3] | MEES E. Entry guidance for human lunar return vehicles with low lift-to-drag ratios[D]. Houston: Rice University, 2010. |
| [4] | BRUNNER C W. Skip entry trajectory planning and guidance[D]. Iowa: Iowa State University, 2008. |
| [5] |
赵彪, 崔乃刚, 郭继峰, 等. 基于虚拟落点策略的月球返回飞船再入制导方法[J].
宇航学报, 2013, 34(2): 170-178.
ZHAO Biao, CUI Naigang, GUO Jifeng, et al. Lunar return entry guidance based on virtual landing point strategy[J]. Journal of Astronautics, 2013, 34(2): 170-178. DOI: 10.3873/j.issn.l000-1328.2013.02.004 |
| [6] |
李贵明, 刘良栋. 过载约束下的探月飞船再入轨迹的在线设计[J].
空间控制技术与应用, 2011, 37(1): 6-10.
LI Guiming, LIU Liangdong. On line design of reentry trajectory under aerodynamic acceleration load constraint of a lunar vehicle[J]. Aerospace Control and Application, 2011, 37(1): 6-10. DOI: 10.3969/j.issn.1674-1579.2011.01.002 |
| [7] | VERNIS P, SPRENG F, GELLY G, et al. Accurate skip-entry guidance for low to medium L/D spacecrafts return missions requiring high range capabilities[C]// AIAA Guidance, Navigation, and Control Conference. Portland, Oregon: AIAA, 2011: 1-15. DOI: 10.2514/6.2011-6649. |
| [8] |
郭敏文, 王大轶. 探月返回器跳跃式再入过载抑制算法研究[J].
宇航学报, 2012, 34(12): 1567-1577.
GUO Minwen, WANG Dayi. Research on load relief method for skip reentry of a lunar return vehicle[J]. Journal of Astronautics, 2012, 34(12): 1567-1577. DOI: 10.3873/j.issn.1000-1328.2013.12.005 |
| [9] |
胡军, 张钊. 载人登月飞行器高速返回再入制导技术研究[J].
控制理论与应用, 2014, 31(12): 1678-1685.
HU Jun, ZHANG Zhao. A study on the reentry guidance for a manned lunar return vehicle[J]. Control Theory & Applications, 2014, 31(12): 1678-1685. DOI: 10.7641/CTA.2014.40908 |
| [10] | LUO Zongfu, ZHANG Hongbo, TANG Guojian. Patched corridor: a novel lateral logic for skip entry guidance[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(5): 1651-1658. DOI: 10.2514/1.G000441 |
| [11] | LU Ping. Predictor-corrector entry guidance for Low-Lifting vehicles[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(4): 1067-1075. DOI: 10.2514/1.32055 |
| [12] | PUTNAM Z R, BARTON G H. An entry trajectory design methodology for lunar return[C]// AIAA Guidance, Navigation, and Control Conference. Chicago, Illinois: AIAA, 2009: 1-17. DOI: 10.2514/6.2009-5773. |
| [13] | NASA. International space station flight crew integration standard (SSP-50005 Revision B NASA-STD-3000/T)[S]. Houston, Texas: NASA, 1999. |
| [14] | XUE Songbai, LU Ping. Constrained predictor-corrector entry guidance[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(4): 1273-1281. DOI: 10.2514/1.49557 |
| [15] |
徐明亮, 陈克俊, 刘鲁华, 等. 高超声速飞行器准平衡滑翔自适应制导方法[J].
中国科学:技术科学, 2012, 55(4): 378-387.
XU Mingliang, CHEN Kejun, LIU Luhua, et al. Quasi-equilibrium glide adaptive guidance for hypersonic vehicles[J]. SCIENCE CHINA Technological Sciences, 2012, 55(4): 378-387. DOI: 10.1007/s11431-011-4727-z |
| [16] | SARAF A, LEAVITT J A, CHEN D T, et al. Design and evaluation of an acceleration guidance algorithm for entry[J]. Journal of Spacecraft and Rockets, 2004, 41(6): 986-996. DOI: 10.2514/1.11015 |
| [17] | SAUNDERS B R. Optimal trajectory design under uncertainty[D]. Cambridge: Massachusetts Institute of Technology, 2012. |
 2017, Vol. 49
2017, Vol. 49


