2. 北京理工大学自动化学院,北京100081;
3. 哈尔滨工业大学 航天学院,哈尔滨150001
2. School of Automation, Beijing Institute of Technology, Beijing 100081, China;
3. School of Astronautics, Harbin Institute of Technology, Harbin 150001, China
长期自主导航技术在运载火箭上面级、轨道转移飞行器、地球卫星等轨道飞行器上具有广阔的应用前景.未来先进的火箭上面级、轨道转移飞行器等需要拓展功能,适应在多星部署、在轨服务等领域的任务需求,需要在飞行时间长、空间跨度大等条件下具备长期在轨精确自主导航的能力[1-2].另外,随着进入轨道的卫星数量的增多、地面测控站的工作量逐渐增大,为降低地面压力,节省成本,也需要进一步发展地球卫星自主导航技术[3-5].因此,为满足轨道飞行器长时间自主导航任务,惯性/天文/卫星组合导航已成为国内外轨道飞行器研制机构首选方案.精度和可靠性是惯性/天文/卫星组合导航系统两项重要的技术指标.发射时的冲击、空间环境的变换、导航器件重复性性能等因素,都会造成组合导航系统器件误差天地不一致的问题,误差在线分离技术已经成为惯性/天文/卫星组合导航系统实现高精度、高可靠性长期导航的关键技术.该技术具有重要的工程应用价值:1) 受火箭发射时刻冲击、空间环境影响,星敏感器等天文姿态器件安装误差变化较大,安装误差分离与补偿技术可提高星敏感器在线使用精度;2) 惯性器件参数误差和一些缓变故障表现类似,通过器件误差的在线估计与补偿,可降低参数误差的影响,有利于故障诊断方法的设计,从而提高系统的可靠性[6];3) 天文导航和卫星导航更新周期低,误差在线标定技术可提高当天文导航和卫星导航无法修正期间的惯性导航的精度.因此,导航器件误差分离技术受到各国科研人员的重视,得到了持续研究.文献[7]整理分析了用四元数描述飞行器姿态动力学方程的方法及其优点.文献[8]建立了飞行器姿态四元数误差、陀螺仪和星敏感器误差模型,利用EKF和UF滤波方法进行误差在线估计,分析了这两种滤波方法对误差估计性能的影响.文献[9]研究了卫星上陀螺误差在轨标定方法.文献[10]利用四元数建立了姿态误差模型,采用Kalman滤波器对惯性/天文组合导航系统陀螺在线标定技术进行了研究.文献[11]研究了利用MPF-KF估计陀螺误差的方法.文献[7]采用欧拉角建立系统误差模型,利用EKF在线估计加速度计和陀螺零偏、星敏感器安装误差和刻度因数误差.
综上所述,文献[7-11]主要围绕基于四元数据描述的飞行器姿态误差建模和滤波方法展开研究,并没有对误差变量的可观测性和精确在线分离的条件进行分析.文献[12]建立了基于欧拉角描述的飞行器姿态误差、速度和位置误差模型,通过滤波方法在线估计导航器件的误差,但是,基于欧拉角的姿态误差模型为非线性模型,且对于一些旋转的角度,无法用欧拉角描述[12],在使用Kalman滤波器的时候会出现问题.鉴于四元数具有非奇异性,基于四元数建立的姿态误差模型为线性模型的优点,本文将在文献[7]及上述其他相关研究成果的基础上,沿用由四元数矢量部分描述姿态误差方程的方法,并进一步进行拓展,用四元数矢量部分建立了完整的姿态、速度误差方程和量测方程,采用Kalman滤波方法实现导航器件误差的在线估计.另外,本文对系统误差模型进行可观测性和可观测度分析,给出了输入条件对可观测度的影响,为导航器件误差的精确在线分离提供了设计依据.结合可观测性分析结果,设计了有效的惯性/天文/卫星组合导航系统误差在线标定策略,获得了理想的试验效果.
1 在线标定算法 1.1 导航器件误差模型完成惯组标定后,若不对陀螺、加速度计进行重新拆装,陀螺和加速度计的安装误差角逐次重复精度高,但陀螺和加速度计零偏、刻度因数误差项逐次通电重复性精度较低,因此,忽略安装误差角,只考虑零偏和刻度因数误差,建立陀螺仪和加速度计的误差模型.
1.1.1 陀螺仪输出误差模型陀螺仪输出记为
| $ \mathit{\boldsymbol{\hat \omega = \omega + }}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_g} \cdot \mathit{\boldsymbol{\hat \omega + }}{\mathit{\boldsymbol{b}}_g} + {\mathit{\boldsymbol{\eta }}_g}, $ | (1) |
式中:
由式 (1) 可得到陀螺的输出误差为
| $ \mathit{\boldsymbol{\delta \omega = \omega }} - \mathit{\boldsymbol{\hat \omega = }} - \left( {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_g}\mathit{\boldsymbol{\hat \omega + }}{\mathit{\boldsymbol{b}}_g} + {\mathit{\boldsymbol{\eta }}_g}} \right). $ | (2) |
加速度计的输出记为
| $ \mathit{\boldsymbol{\hat f = f + }}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_a}\mathit{\boldsymbol{\hat f}} + {\mathit{\boldsymbol{b}}_a} + {\mathit{\boldsymbol{\eta }}_a}. $ | (3) |
式中:
由式 (3) 可得到加速度计的输出误差为
| $ \delta \mathit{\boldsymbol{f = f}} - \mathit{\boldsymbol{\hat f}} = - \left( {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_a}\mathit{\boldsymbol{\hat f}} + {\mathit{\boldsymbol{b}}_a} + {\mathit{\boldsymbol{\eta }}_a}} \right). $ |
星敏感器测量星光确定的姿态四元数表示为
| $ {{\mathit{\boldsymbol{\hat q}}}_s} = {\mathit{\boldsymbol{q}}_s} \otimes {\mathit{\boldsymbol{q}}_\psi }. $ |
式中:
根据理想四元数qg和捷联惯性导航计算确定的四元数
| $ \delta {\mathit{\boldsymbol{q}}_\varphi } = {\mathit{\boldsymbol{q}}_g} \otimes \mathit{\boldsymbol{\hat q}}_g^{ - 1}. $ | (4) |
由于四元数运动满足如下关系:
| $ \frac{{{\rm{d}}{\mathit{\boldsymbol{q}}_g}}}{{{\rm{d}}t}} = \frac{1}{2}\omega \otimes {\mathit{\boldsymbol{q}}_g}, $ | (5) |
| $ \frac{{{\rm{d}}{{\mathit{\boldsymbol{\hat q}}}_g}}}{{{\rm{d}}t}} = \frac{1}{2}\mathit{\boldsymbol{\hat \omega }} \otimes {{\mathit{\boldsymbol{\hat q}}}_g}. $ | (6) |
对式 (4) 求导数,并将式 (5),(6) 代入式 (4) 可得
| $ \begin{array}{l} \frac{{{\rm{d}}\left( {\delta {\mathit{\boldsymbol{q}}_\varphi }} \right)}}{{{\rm{d}}t}} = \frac{{{\rm{d}}{\mathit{\boldsymbol{q}}_g}}}{{{\rm{d}}t}} \otimes \mathit{\boldsymbol{\hat q}}_g^{ - 1} + {\mathit{\boldsymbol{q}}_g} \otimes \frac{d}{{{\rm{d}}t}}\left( {\mathit{\boldsymbol{\hat q}}_g^{ - 1}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}\mathit{\boldsymbol{\omega }} \otimes \delta {\mathit{\boldsymbol{q}}_\varphi } - \frac{1}{2}\delta {\mathit{\boldsymbol{q}}_\varphi } \otimes \mathit{\boldsymbol{\hat \omega }}, \end{array} $ |
式中,
| $ \begin{array}{l} \frac{{{\rm{d}}\left( {\delta {\mathit{\boldsymbol{q}}_\varphi }} \right)}}{{{\rm{d}}t}} = \frac{1}{2}\left[ {\mathit{\boldsymbol{\hat \omega }} \otimes \delta {\mathit{\boldsymbol{q}}_\varphi } - \delta {\mathit{\boldsymbol{q}}_\varphi } \otimes \mathit{\boldsymbol{\hat \omega }}} \right] + \frac{1}{2}\delta {\mathit{\boldsymbol{q}}_\varphi } \otimes \delta \mathit{\boldsymbol{\omega }},\\ \mathit{\boldsymbol{\hat \omega }} \otimes \delta {\mathit{\boldsymbol{q}}_\varphi } - \delta {\mathit{\boldsymbol{q}}_\varphi } \otimes \mathit{\boldsymbol{\hat \omega }} = \left[ {\begin{array}{*{20}{c}} 0\\ {2\mathit{\boldsymbol{\hat \omega }} \otimes \delta {{\mathit{\boldsymbol{\vec q}}}_\varphi } } \end{array}} \right]. \end{array} $ |
其中,
| $ \delta {\mathit{\boldsymbol{q}}_\varphi } \otimes \delta \omega = \left[ {\begin{array}{*{20}{c}} 0 & { - \delta {\omega _x}} & { - \delta {\omega _y}} & { - \delta {\omega _z}}\\ {\delta {\omega _x}} & 0 & {\delta {\omega _z}} & { - \delta {\omega _y}}\\ {\delta {\omega _y}} & { - \delta {\omega _z}} & 0 & {\delta {\omega _x}}\\ {\delta {\omega _z}} & {\delta {\omega _y}} & { - \delta {\omega _x}} & 0 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {\delta {q_{\varphi 0}}}\\ {\delta {q_{\varphi 1}}}\\ {\delta {q_{\varphi 2}}}\\ {\delta {q_{\varphi 3}}} \end{array}} \right], $ |
又因为δqφ0≈1,忽略二阶项可得
| $ \delta {\mathit{\boldsymbol{q}}_\varphi } \otimes \delta \mathit{\boldsymbol{\omega = }}\left[ {\begin{array}{*{20}{c}} 0\\ {\delta \omega } \end{array}} \right]. $ |
因此,δqφ的导数为
| $ \frac{{{\rm{d}}\left( {\delta {\mathit{\boldsymbol{q}}_\varphi }} \right)}}{{{\rm{d}}t}} = - \left[ {\begin{array}{*{20}{c}} 0\\ {\mathit{\boldsymbol{\hat \omega }} \otimes \delta {{\mathit{\boldsymbol{\vec q}}}_\varphi } } \end{array}} \right] + \frac{1}{2}\left[ {\begin{array}{*{20}{c}} 0\\ {\delta \mathit{\boldsymbol{\omega }}} \end{array}} \right], $ |
将矢量和标量部分分开写,可得:
| $ \frac{{{\rm{d}}\left( {\delta {{\mathit{\boldsymbol{\vec q}}}_\varphi }} \right)}}{{{\rm{d}}t}} = - \mathit{\boldsymbol{\hat \omega }} \otimes \delta {{\mathit{\boldsymbol{\vec q}}}_\varphi } + \frac{1}{2}\delta \mathit{\boldsymbol{\omega }}, $ | (7) |
| $ \frac{{{\rm{d}}\left( {\delta {\mathit{\boldsymbol{q}}_{\varphi 0}}} \right)}}{{{\rm{d}}t}} = 0. $ | (8) |
将陀螺的输出误差模型式 (2) 代入式 (7),得到四元数误差模型:
| $ \frac{{{\rm{d}}\left( {\delta {{\mathit{\boldsymbol{\vec q}}}_\varphi }} \right)}}{{{\rm{d}}t}} = - \mathit{\boldsymbol{\hat \omega }} \otimes \delta {{\mathit{\boldsymbol{\vec q}}}_\varphi } - \frac{1}{2}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_g}\mathit{\boldsymbol{\hat \omega }} + {\mathit{\boldsymbol{b}}_g} + {\mathit{\boldsymbol{\eta }}_g}} \right). $ |
对于捷联安装的加速度计来说,速度测量方程可以描述为
| $ \frac{{{\rm{d}}\hat v}}{{{\rm{d}}t}} = \mathit{\boldsymbol{C}}_g^{i'}\mathit{\boldsymbol{C}}_{i'}^i{{\mathit{\boldsymbol{\hat f}}}_b} - {{\mathit{\boldsymbol{\hat g}}}_i}. $ | (9) |
式中:Cgi′为惯组本体坐标系到发射惯性系的姿态矩阵;Ci′i为捷联导航数学平台失准角;
理想的速度方程为
| $ \frac{{{\rm{d}}v}}{{{\rm{d}}t}} = \mathit{\boldsymbol{C}}_g^{i'}\mathit{\boldsymbol{C}}_{i'}^i{\mathit{\boldsymbol{f}}_b} - {\mathit{\boldsymbol{g}}_i}. $ | (10) |
忽略引力误差,式 (10) 减式 (9),可得:
| $ \begin{array}{l} \frac{{{\rm{d}}v}}{{{\rm{d}}t}} - \frac{{{\rm{d}}\hat v}}{{{\rm{d}}t}} = \mathit{\boldsymbol{C}}_g^{i'}\mathit{\boldsymbol{C}}_{i'}^i{\mathit{\boldsymbol{f}}_b} - {\mathit{\boldsymbol{g}}_i} - \left( {\mathit{\boldsymbol{C}}_g^{i'}{{\mathit{\boldsymbol{\hat f}}}_b} - {{\mathit{\boldsymbol{\hat g}}}_i}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{C}}_g^{i'}\left( {\mathit{\boldsymbol{I + }}\varphi \times } \right){\mathit{\boldsymbol{f}}_b} - \mathit{\boldsymbol{C}}_g^{i'}{{\mathit{\boldsymbol{\hat f}}}_b} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{C}}_g^{i'} \cdot \varphi \times {\mathit{\boldsymbol{f}}_b} + \mathit{\boldsymbol{C}}_g^{i'}\left( {{\mathit{\boldsymbol{f}}_b} - {{\mathit{\boldsymbol{\hat f}}}_b}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{C}}_g^{i'} \cdot \left( {\mathit{\boldsymbol{I + }}\varphi \times - \mathit{\boldsymbol{I}}} \right){\mathit{\boldsymbol{f}}_b} + \mathit{\boldsymbol{C}}_g^{i'}\left( {{\mathit{\boldsymbol{f}}_b} - {{\mathit{\boldsymbol{\hat f}}}_b}} \right), \end{array} $ | (11) |
| $ \mathit{\boldsymbol{I + }}\varphi \times - \mathit{\boldsymbol{I}} = \left[ {\begin{array}{*{20}{c}} 0 & {2\delta {q_{\varphi 3}}} & { - 2\delta {q_{\varphi 2}}}\\ { - 2\delta {q_{\varphi 3}}} & 0 & {2\delta {q_{\varphi 1}}}\\ {2\delta {q_{\varphi 2}}} & { - 2\delta {q_{\varphi 1}}} & 0 \end{array}} \right], $ | (12) |
| $ \varphi \times {\mathit{\boldsymbol{f}}_b} = 2 \cdot \left[ {{\mathit{\boldsymbol{f}}_b} \times } \right] \cdot \delta \overrightarrow {{\mathit{\boldsymbol{q}}_\varphi }} . $ | (13) |
忽略二阶小量得到速度误差方程:
| $ \frac{{{\rm{d}}\left( {\delta v} \right)}}{{{\rm{d}}t}} = 2\mathit{\boldsymbol{C}}_g^{i'} \cdot {{\mathit{\boldsymbol{\hat f}}}_b} \times \delta \mathit{\boldsymbol{\vec q}} + \mathit{\boldsymbol{C}}_g^{i'}\delta {\mathit{\boldsymbol{f}}_b}. $ | (14) |
将加速度计的输出误差式 (3) 代入式 (14) 得到:
| $ \frac{{{\rm{d}}\left( {\delta v} \right)}}{{{\rm{d}}t}} = 2\mathit{\boldsymbol{C}}_g^{i'} \cdot \left[ {{{\mathit{\boldsymbol{\hat f}}}_b} \times } \right] \cdot \delta \mathit{\boldsymbol{\vec q}} - \mathit{\boldsymbol{C}}_g^{i'}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_a}\mathit{\boldsymbol{\hat f + }}{\mathit{\boldsymbol{b}}_a} + {\mathit{\boldsymbol{\eta }}_a}} \right). $ |
位置误差方程为
| $ \frac{{{\rm{d}}\left( {\delta \mathit{\boldsymbol{p}}} \right)}}{{{\rm{d}}t}} = \frac{{{\rm{d}}\left( {\delta v} \right)}}{{{\rm{d}}t}}. $ |
导航坐标系为发射惯性系,组合导航系统的状态方程为捷联惯导的误差方程,状态方程为
| $ \frac{{{\rm{d}}\left( {\mathit{\boldsymbol{X}}\left( t \right)} \right)}}{{{\rm{d}}t}} = \mathit{\boldsymbol{A}}\left( t \right) \cdot \mathit{\boldsymbol{X}}\left( t \right) + \mathit{\boldsymbol{G}}\left( t \right) \cdot \mathit{\boldsymbol{W}}\left( t \right). $ |
式中:A(t) 为系统的状态转移矩阵;G(t) 为系统的噪声系数矩阵;W(t) 为系统噪声向量; X(t) 为t时刻的系统状态矢量.结合导航器件、组合导航系统的误差模型,系统状态误差变量取
| $ \mathit{\boldsymbol{X = }}\left[ {\begin{array}{*{20}{c}} {\delta {{\mathit{\boldsymbol{\vec q}}}_\varphi }} & {\delta \mathit{\boldsymbol{p}}} & {\delta \mathit{\boldsymbol{v}}} & {{\mathit{\boldsymbol{b}}_g}} & {{\mathit{\boldsymbol{b}}_a}} & {{{\mathit{\boldsymbol{\vec q}}}_\varphi }} & {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_g}} & {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_a}} \end{array}} \right]_{1 \times 24}^{\rm{T}}. $ | (15) |
式中:状态变量为24个,分别为数学平台失准角误差、位置误差、速度误差、陀螺零偏误差、加速度计零偏误差、星敏感器安装误差 (用四元数的矢量部分表示)、陀螺刻度因数误差、加速度计刻度因数.
1.3.2 观测方程星敏感器体坐标系到发射惯性系的姿态矩阵记为Csi, 得到惯性姿态矩阵和星光姿态矩阵间的误差为
| $ \mathit{\boldsymbol{C}}_g^{i'}\mathit{\boldsymbol{C}}_i^s = \left[ {\begin{array}{*{20}{c}} 1 & { - {\psi _z}} & {{\psi _y}}\\ {{\psi _z}} & 1 & { - {\psi _x}}\\ { - {\psi _y}} & {{\psi _x}} & 1 \end{array}} \right] = \mathit{\boldsymbol{I + \psi }} \times . $ | (16) |
考虑到星敏感器安装误差和惯组数学平台误差角,得到:
| $ \mathit{\boldsymbol{C}}_g^{i'}\mathit{\boldsymbol{C}}_i^s = \mathit{\boldsymbol{C}}_g^{i'}\mathit{\boldsymbol{C}}_i^s\mathit{\boldsymbol{C}}_{i'}^g\mathit{\boldsymbol{C}}_i^{i'} = \mathit{\boldsymbol{C}}_g^{i'}\left( {\mathit{\boldsymbol{I + }}\varphi \times } \right)\mathit{\boldsymbol{C}}_{i'}^g\left( {\mathit{\boldsymbol{I}} - \varphi \times } \right). $ | (17) |
式中:Cgs为惯组和星敏感器间的安装误差矩阵;φ为星敏感器安装误差角。对比式 (16),(17),忽略二阶误差, 可以得到:
| $ \psi \times = \varphi \times - \mathit{\boldsymbol{C}}_g^{i'}\varphi \times . $ | (18) |
由式 (13) 可知失准角和四元数误差存在如下关系:
| $ \varphi \times = 2{\left[ {\delta {{\mathit{\boldsymbol{\vec q}}}_\varphi } \times } \right]^{\rm{T}}}, $ | (19) |
将式 (19) 代入式 (18),可以得到:
| $ \delta {{\mathit{\boldsymbol{\vec q}}}_\psi } \times = \delta {{\mathit{\boldsymbol{\vec q}}}_\varphi } \times - \mathit{\boldsymbol{C}}_g^{i'}\delta {{\mathit{\boldsymbol{\vec q}}}_\varphi } \times , $ |
所以
| $ \delta {{\mathit{\boldsymbol{\vec q}}}_\psi } = \delta {{\mathit{\boldsymbol{\vec q}}}_\varphi } - \mathit{\boldsymbol{C}}_g^{i'}\delta {{\mathit{\boldsymbol{\vec q}}}_\varphi }. $ | (20) |
以姿态四元数误差和位置误差作为观测量,惯性/天文/卫星组合导航系统测量方程为
| $ \mathit{\boldsymbol{Z}}\left( t \right) = {\left[ {\begin{array}{*{20}{c}} {\delta {{\mathit{\boldsymbol{\vec q}}}_\psi }}\\ {\delta \mathit{\boldsymbol{p}}} \end{array}} \right]_{6 \times 1}} = \mathit{\boldsymbol{H}}\left( t \right)\mathit{\boldsymbol{X}}\left( t \right) + \mathit{\boldsymbol{V}}\left( t \right). $ |
式中:
根据式 (20),得到:
| $ \mathit{\boldsymbol{H}}\left( t \right) = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}} & { - \mathit{\boldsymbol{C}}_g^{i'}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}}\\ {{0_{3 \times 3}}} & {{\mathit{\boldsymbol{I}}_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}} \end{array}} \right]_{6 \times 24}}. $ |
上述各物理量在应用过程中实际上都不是连续的模拟量,而是离散量,需要把上述Kalman滤波方程离散化.离散化公式为:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}_{k,k - 1}} = \sum\limits_{n = 0}^\infty {{{\left[ {A\left( {{t_k}} \right) \cdot \Delta } \right]}^n}/n!} ,}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{k - 1}} = \left\{ {\sum\limits_{n = 0}^\infty {{{\left[ {\frac{1}{{n!}}\left( {A\left( {{t_k}} \right) \cdot \Delta } \right)} \right]}^{n - 1}}} } \right\}\mathit{\boldsymbol{G}}\left( {{t_k}} \right) \cdot \Delta .} \end{array} $ |
式中:Δ为Kalman滤波周期,n为离散化阶数.离散化的系统状态方程和量测方程可表示为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{X}}_k} = {\mathit{\boldsymbol{F}}_{k.k - 1}}{\mathit{\boldsymbol{X}}_{k - 1}} + {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{k - 1}}{\mathit{\boldsymbol{W}}_{k - 1}},\\ {\mathit{\boldsymbol{Z}}_k} = {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{X}}_k} + \mathit{\boldsymbol{V}}. \end{array} \right. $ |
这样就可以按照下列离散Kalman滤波方程进行滤波解算, 开环Kalman滤波方程参见文献[14].
2 惯性/天文/卫星组合导航误差可观测性分析在线标定算法建立了惯性/天文/卫星组合导航系统的状态方程和量测方程,该系统为线性时变系统,系统的可观测性和状态变量的可观测度与误差变量可分离的数量和精度直接相关.
2.1 PWCS可观测性分析定理不考虑系统噪声,第j个时间段离散系统模型为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{X}}\left( {k + 1} \right) = {\mathit{\boldsymbol{F}}_j}X\left( k \right),\\ {Z_j}\left( k \right) = {\mathit{\boldsymbol{H}}_j}X\left( k \right). \end{array} \right. $ | (21) |
式中:
系统的总可观测矩阵TOM为
| $ \mathit{\boldsymbol{Q}}\left( r \right) = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Q}}_1}} & {{\mathit{\boldsymbol{Q}}_2}F_1^{n - 1}} & \cdots & {{\mathit{\boldsymbol{Q}}_r}\mathit{\boldsymbol{F}}_{r - 1}^{n - 1} \cdots \mathit{\boldsymbol{F}}_1^{n - 1}} \end{array}} \right]^{\rm{T}}}, $ |
其中
| $ \mathit{\boldsymbol{Q}}_j^{\rm{T}} = \left[ {\begin{array}{*{20}{c}} {{{\left( {{\mathit{\boldsymbol{H}}_j}} \right)}^{\rm{T}}},} & {{{\left( {{\mathit{\boldsymbol{H}}_j}{\mathit{\boldsymbol{F}}_j}} \right)}^{\rm{T}}},} & { \cdots ,} & {{{\left( {{\mathit{\boldsymbol{H}}_j}\mathit{\boldsymbol{F}}_1^{n - 1}} \right)}^{\rm{T}}}} \end{array}} \right]. $ |
如果矩阵Q(r) 的秩为n,则系统是完全可观测的.利用Q(r) 进行系统的可观测性分析计算量大,且无法确定每个状态变量的可观测程度.文献[15]提出了基于奇异值分解理论的系统可观测性分析方法,利用提取可观测性矩阵SOM代替TOM分析系统的可观测性,SOM为Qs(r)=[Q1 Q2 … Qr]T,结合奇异值分解方法,可以同时得到可观测性和可观测度的分析结果.为了利用SOM分析可观测性,有如下定理[15].
定理1 如果Fjx = x, ∀x∈null{Qj(r)}, 1≤j≤r, 则null{Q(r)}=null{Qs(r)},rank{Q(r)}=rank{Qs(r)}.
定理2 如果
定理3 如果Fj是对应Aj和Δj的离散化的转移矩阵,其中Δj为采样时间间隔,则
基于奇异值分解理论的系统可观测性分析方法参见文献[15].
2.2 基于奇异值分解理论的系统可观测性分析方法在本系统上的适用性证明将第j个时间段组合导航系统连续的状态方程和量测方程记为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot X}}\left( t \right) = {\mathit{\boldsymbol{A}}_j}\mathit{\boldsymbol{X}}\left( t \right),\\ {\mathit{\boldsymbol{Z}}_j}\left( t \right) = {\mathit{\boldsymbol{H}}_j}\mathit{\boldsymbol{X}}\left( t \right). \end{array} \right. $ | (22) |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_j} = {{\left[ {\begin{array}{*{20}{c}} {{{\left( {{\mathit{\boldsymbol{A}}_{11}}} \right)}_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}} & {{{\left( {{\mathit{\boldsymbol{A}}_{12}}} \right)}_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}} & {{{\left( {{\mathit{\boldsymbol{A}}_{13}}} \right)}_{3 \times 3}}} & {{0_{3 \times 3}}}\\ {{0_{3 \times 3}}} & {{0_{3 \times 3}}} & {{\mathit{\boldsymbol{I}}_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}}\\ {{{\left( {{\mathit{\boldsymbol{A}}_{21}}} \right)}_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}} & {{{\left( {{\mathit{\boldsymbol{A}}_{22}}} \right)}_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}} & {{{\left( {{\mathit{\boldsymbol{A}}_{23}}} \right)}_{3 \times 3}}}\\ {} & {} & {} & {{0_{15 \times 24}}} & {} & {} & {} & {} \end{array}} \right]}_{24 \times 24}},}\\ {{\mathit{\boldsymbol{H}}_j} = {{\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}} & {{\mathit{\boldsymbol{h}}_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}}\\ {{0_{3 \times 3}}} & {{\mathit{\boldsymbol{I}}_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}} & {{0_{3 \times 3}}} \end{array}} \right]}_{6 \times 24}}.} \end{array} $ |
提取可观测矩阵为
| $ {{\mathit{\boldsymbol{\tilde Q}}}_j} = {\left[ {{\mathit{\boldsymbol{H}}_j},{\mathit{\boldsymbol{H}}_j}{\mathit{\boldsymbol{A}}_j}, \cdots ,{\mathit{\boldsymbol{H}}_j}\mathit{\boldsymbol{A}}_j^{k - 1}} \right]^{\rm{T}}}. $ | (23) |
令
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{x}}_1} + \mathit{\boldsymbol{h}} \cdot {\mathit{\boldsymbol{x}}_6} = 0,\\ {\mathit{\boldsymbol{x}}_2} = 0,\\ {\mathit{\boldsymbol{A}}_{11}} \cdot {\mathit{\boldsymbol{x}}_1} + {\mathit{\boldsymbol{A}}_{12}} \cdot {\mathit{\boldsymbol{x}}_4} + {\mathit{\boldsymbol{A}}_{13}} \cdot {\mathit{\boldsymbol{x}}_7} = 0,\\ {\mathit{\boldsymbol{x}}_3} = 0,\\ n{\mathit{\boldsymbol{A}}_{11}}{n^2}{\mathit{\boldsymbol{x}}_1} + {\mathit{\boldsymbol{A}}_{11}} \cdot {\mathit{\boldsymbol{A}}_{12}} \cdot {\mathit{\boldsymbol{x}}_4} + {\mathit{\boldsymbol{A}}_{11}} \cdot {\mathit{\boldsymbol{A}}_{13}} \cdot {\mathit{\boldsymbol{x}}_7} = 0,\\ {\mathit{\boldsymbol{A}}_{21}} \cdot {\mathit{\boldsymbol{x}}_1} + {\mathit{\boldsymbol{A}}_{22}} \cdot {\mathit{\boldsymbol{x}}_5} + {\mathit{\boldsymbol{A}}_{23}} \cdot {\mathit{\boldsymbol{x}}_8} = 0,\\ \vdots \end{array} \right. $ | (24) |
式中:x1~ x6与式 (15) 中的误差变量相对应,分别表示数学平台失准角误差、位置误差等.由式 (24) 可知,Aj· X =0,即X∈null{Aj},所以
飞行器在轨运动可以分为3种基本类型:1) 无动力飞行状态;2) 进行姿态机动;3) 线加减速运动.针对这3种基本类型,设计的可观测性分析的输入条件为:状态Ⅰ为无动力飞行状态,陀螺测量飞行器相对惯性空间的转动角速率,通常该角速率较小,这里取三轴向陀螺敏感的角速率均为2.4×10-4 (°)/s;状态Ⅱ为角运动状态下,x,y,z轴向角速率分别为0, 0, 10(°)/s;状态Ⅲ为加减速运动条件下,x,y,z轴向加速度分别为,0, 20, 0 m/s2.利用基于奇异值分解理论的系统可观测性分析方法对系统的可观测性进行了分析,可观测性分析结果见表 1,表 1中为在3种运动条件下,状态变量对应的奇异值,奇异值越大,可观测度越大,变量的可观测性越强,奇异值小于5×10-8时,对应的状态不可观测[16].在状态Ⅰ条件下,有15个状态变量的奇异值较大,其他的状态变量的奇异值基本为0.可观测的变量为数学平台失准角误差、位置误差、速度误差、陀螺零偏误差、加速度计零偏误差.在状态Ⅱ条件下,与状态Ⅰ相比,星敏感器安装误差和y轴加速度计刻度因数误差可观测,加表零偏变为了不可观测.在状态Ⅲ条件下,与状态Ⅰ结果相比,星敏感器安装误差和z轴陀螺刻度因数误差可观测,z轴陀螺零偏不可观测.因此,加入线加速度机动或角速率机动,可提高星敏感器器安装误差的可观测性; 加入线加速度机动,可提高对应轴向上的加表的刻度因数误差的可观测度; 加入角速率机机动,可提高对应轴向上的陀螺刻度因数误差的可观测度.也就是在一定的机动条件下,本文24个误差变量均可观测.
| 表 1 不同运动状态下的奇异值 Table 1 Singular value of different moving states |
利用在线标定的算法,编写了组合导航系统误差在线估计仿真程序,其中状态变量为24维,初值为0,观测变量6维,采用标准的开环Kalman滤波方法进行误差估计,滤波方程系数矩阵离散化处理取3阶.
仿真试验中假设三轴向的陀螺随机噪声均为0.2(°)/h, 三轴向的陀螺零偏误差为ωx=1×10-4 rad/s, ωy=2×10-4 rad/s, ωz=3×10-4 rad/s, 陀螺刻度因数误差均为3×10-5;三轴向加速度计随机噪声均为1×10-4 m/s2, 陀螺和加速度计的更新周期2 ms;星敏感器的安装误差分别为φx=1×10-3 rad, φy=2×10-3 rad, φz=3×10-3 rad;星敏感器定姿精度为10″(1σ), 卫星导航的定位精度为10 m (1σ).
3.2 仿真试验结果根据系统的可观测度分析结果,导航器件误差在线标定策略为:1) 依次在惯组3个轴向加入100(°)/s的角速率机动,取加入角速率机动对应时间段的陀螺刻度因数误差滤波估计结果,得到陀螺刻度因数误差数据.在该条件下,也可以同时估计出其他21个误差变量,但是由表 1中的数据可知,其他变量可观测度相对较差,故不作为最终的分离结果;2) 依次在惯组3个轴向加入50 m/s2的加速度机动,分离出加表刻度因数误差,同时估计出星敏感器安装误差;3) 在惯组三轴向角速率均为2.4×10-4 (°)/s,加速度均为0 m/s2时,估计出陀螺零偏误差、加速度计零偏误差.
导航器件参数误差估计结果如图 1~图 5所示,图中结果表明,15项参数误差均能收敛到稳定值.滤波稳定后,陀螺刻度因数误差的精度优于1×10-6,加速度计的刻度因数误差优于2×10-6,星敏感器安装误差的精度优于5×10-6 rad,陀螺零偏误差的精度1.5×10-6 rad/s,加速度计零偏误差优于2.75×10-4 m/s2,该试验结果表明,利用本文的在线估计方法,各参数误差的在线标定精度均能提高一个数量级,仿真试验结果与可观测性分析结果一致,因此本文的误差标定模型和标定正确,通过本方法可有效提高导航精度.
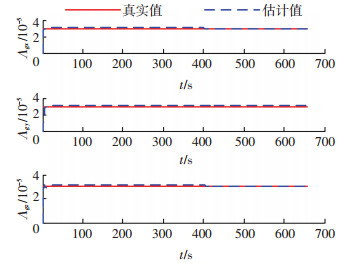
|
图 1 陀螺刻度因数误差 Figure 1 Gyro scale factor errors |
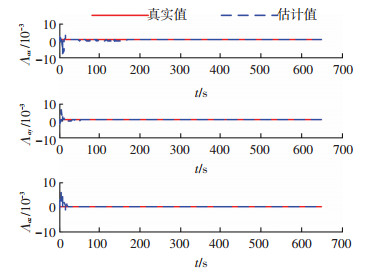
|
图 2 加速度计刻度因数误差 Figure 2 Accelerometer scale factor errors |
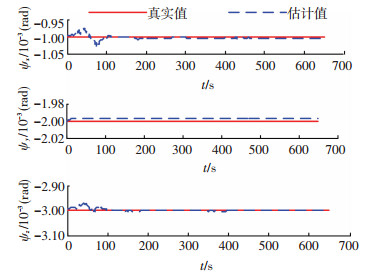
|
图 3 星敏感器安装误差 Figure 3 Star tracker misalignment errors |

|
图 4 陀螺零偏误差 Figure 4 Gyro bias errors |
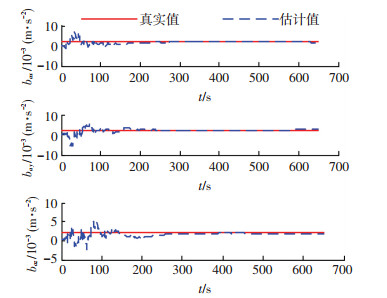
|
图 5 加速度计零偏误差 Figure 5 Accelerometer bias errors |
1) 为了提高惯性/天文/卫星组合导航系统长期在轨工作的精度,完善了基于四元数描述的惯性/天文/卫星组合导航误差和各惯性器件误差模型,利用分段定常系统 (PWCS) 定理,分析了不同输入条件下系统状态变量的可观测性和可观测度.为各项误差的有效分离提供了理论依据。
2) 结合惯性/天文/卫星组合导航系统可观测性和可观测度分析结果,提出了利用Kalman滤波技术在线估计惯性/天文/卫星组合导航误差和导航器件误差的标定策略,仿真试验验证了该策略的有效性和精度,该在线标定方法、可观测性分析结果和试验结果对在线标定技术在工程上的应用具有重要的参考价值.
| [1] | DRESSLER G, MATUSZAK L, STEPHENSON D D. Study of a high-energy upper stage for future shuttle missions[C]//Proceedings of the 39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit. Huntsville, Alabama: AIAA, 2003:1-10. DOI: 10.2514/6.2003-5128. |
| [2] | LEESON J. Feasibility study of the multipurpose orbitally deployed upper stage (MODUS) platform[C]//Proceedings of the 65th International Astronautical Congress. Toronto, Canada:[s.n].2014. |
| [3] | WHITE R L, GOUNLEY R B. Satellite autonomous navigation with SHAD[R].CSDL-R-1982, Cambride: The Charles Stark Draper Laboratory, Inc, 1987. |
| [4] | HICKS K D, IESEL W E. Autonomous orbit determination system for earth satellites[J]. Journal of Guidance, Control and Dynamics, 1992, 15(3): 562-566. DOI: 10.2514/3.20876 |
| [5] | GOTTZEIN E, FICHTER W, JABLONSKI A, et al. Challenges in control and autonomous of communications Satellites[J]. Control Engineering Practice, 2000, 8(4): 409-427. DOI: 10.1016/S0967-0661(99)00171-9 |
| [6] | ZONG Hua, WANG Bo, LIU Zhun, et al. Fault detection in SINS/CNS/GPS integrated system based on federated filter[C]//Proceedings of the 33nd Chinese Control Conference. Nan Jing:IEEE, 2014: 608-612. DOI: 10.1109/ChiCC.2014.6896694. |
| [7] | LEFFERTS E J, MARKLEY F L, SHUSTER M D. Kalman filtering for spacecraft attitude estimation[J]. Journal of Guidance, Control, and Dynamics, 1982, 5(5): 417-429. DOI: 10.2514/3.56190 |
| [8] | KOKLAM LAI, JOHN L, CRASSIDIS, et al. In-space spacecraft alignment calibration using the unscented filter[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. Austin, Texas: AIAA, 2003:1-11. DOI: 10.2514/6.2003-5563. |
| [9] |
陈雪芹, 耿云海, 何蕊. 基于二阶非线性滤波的星上陀螺在轨标定[J].
哈尔滨工业大学学报, 2008, 40(11): 1690-1695.
CHEN Xueqin, GENG Yunhai, HE Rui. On-orbit calibration of satellite gyro based on second-order nonlinear filtering[J]. Journal of Harbin Institute of Technology, 2008, 40(11): 1690-1695. DOI: 10.3321/j.issn:0367-6234.2008.11.003 |
| [10] |
肇慧, 沈继红, 陈涛. SINS/CNS组合导航系统陀螺在线标定技术[J].
计算机工程与应用, 2013, 49(19): 1-4.
ZHAO Hui, SHEN Jihong, CHEN Tao. On-line calibration of gyro in SINS/CNS integrated navigation system[J]. Computer Engineering and Applications, 2013, 49(19): 1-4. DOI: 10.3778/j.issn.1002-8331.1304-0227 |
| [11] | HAO Yanling, MU Hongwei, LIU Xintao. On-line calibration technology for SINS/CNS based on MPF-KF[C]// Proceedings of 2012 IEEE International Conference on Mechatronics and Automation. Cheng Du: IEEE, 2012: 1132-1136. DOI: 10.1109/ICMA.2012.6283409. |
| [12] | VETH M M, RAQUET J. Alignment and calibration of optical and inertial sensors using stellar observations[C]//Proceedings of the 18th International Technical Meeting of the Satellite Division of the Institute of Navigation. Long Beach, CA: IEEE, 2005:2494-2503. |
| [13] | 秦永元. 惯性导航[M]. 北京: 科学出版社, 2006: 358-359. |
| [14] | ZONG Hua, WANG Bo, LIU Zhun, et al. SINS/CNS/GNSS integrated navigation scheme for advanced upper stage[C]// Proceedings of the 2014 International Conference on Mechatronics and Control. Jinzhou: IEEE, 2014:2109-2113. DOI: 10.1109/ICMC.2014.7231938. |
| [15] | 万德钧, 房建成. 惯性导航初始对准[M]. 南京: 东南大学出版社, 1998: 100-106. |
| [16] |
周卫东, 蔡佳楠, 孙龙, 等. GPS/SINS超紧组合导航系统可观测性分析[J].
北京航空航天大学学报, 2013, 39(9): 1157-1162.
ZHOU Weidong, CAI Jianan, SUN Long, et al. Observability analysis of GPS/SINS ultra-tightly coupled system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(9): 1157-1162. |
 2017, Vol. 49
2017, Vol. 49


