全球卫星导航系统 (global navigation satellite system,GNSS) 是一个能够连续、全天候为用户提供导航、定位以及授时服务的无线电导航系统.近年来,GNSS发展迅速,在航海、测绘、交通、机械控制等领域得到了广泛应用.但是,卫星信号到达地面时强度很弱,只有大约-160 dBW,并且存在着诸如电离层闪烁、多路径效应、电磁干扰、卫星数量不足等因素可能使GNSS功能失效,这些因素称为脆弱性因素.
脆弱性这一概念刚被提起时,文献[1]对交通领域的GPS脆弱性进行了初步评估.随后,各国学者对GNSS脆弱性问题进行了研究.文献[2-3]分析了电离层闪烁对GPS信号的影响;文献[4-5]用自适应滤波的手段实现了对连续GPS测量信号的多径缓解;文献[6-7]提出了依据信号强度、噪声强度和载噪比进行抗欺骗干扰技术的方法;文献[8]进行了针对精密单点定位的钟跳修复研究等等.这些研究以定性研究或单项技术研究为主,定量的GNSS整体脆弱性研究刚刚起步.在有限的成果中,尚未出现适用于评价城市道路GNSS脆弱性的评估方法.例如,文献[9]设计的基于D-S证据理论的脆弱性评估方法.通过大量长期观测计算载噪比理论值,通过GNSS基站的自身精确定位计算几何精度因子理论值.但对于城市普通道路环境,难以满足上述要求,所以该方法难以评估城市道路GNSS脆弱性.文献[10]设计的基于用户端适用性的GNSS脆弱性评估方法.该方法以用户为核心,通过用户提供的“适用度”与“容忍度”两个指标确定评估指标的应用适用性,然后融合各个评估指标的应用适用性得到适用度.但是,不同交通用户提供的“适用度”与“容忍度”不尽相同且难以得到.
本文针对不同城市道路环境的特点,选取了3个GNSS脆弱性评价参数,提出了基于信息熵权与正、负理想方案“距离”的脆弱性评估方法.利用数据融合算法,对不同城市道路环境完成了GNSS脆弱性性能排序.
1 城市道路GNSS脆弱性及脆弱性因素 1.1 GNSS脆弱性与系统的关系[11]GNSS脆弱性与系统的关系体现在:1) 脆弱性是GNSS的固有属性;2) 脆弱性含义,为系统受到威胁的可能性; 3) 脆弱性表现,为系统受到威胁时,威胁对系统的影响程度.
1.2 GNSS脆弱性与用户的关系[10]GNSS脆弱性与用户的关系体现在:1) GNSS脆弱性的评估紧紧依赖于用户需求;2) 对于不同用户,GNSS脆弱性的评估指标可能不同;3) 对于同一用户,GNSS脆弱性的评估转变为对GNSS性能的评估.
对于城市道路上的交通用户,上述总结仍然适用.因此,对城市道路GNSS脆弱性的评估,可转变为对不同城市道路环境GNSS性能的评估.
对于城市道路环境,GNSS脆弱性因素可分为3大类:系统相关脆弱性、建筑物遮挡相关脆弱性和电磁干扰相关脆弱性.
1) 系统相关脆弱性.卫星数量不足时,例如当GPS卫星数量少于24颗时,用户服务范围将下降,用户服务可能中断;卫星时钟异常时,例如当卫星时钟出现钟漂或钟跳时,卫星时钟变得不可预测,最后钟差缓慢增长使系统功能失效.
电离层闪烁,是电离层对卫星信号造成延时中比较严重的部分.它指卫星信号穿过电离层时,由于电离层中的离子浓度分布不均匀,载波将出现幅值和相位的剧烈变化.当接收机接收到受到电离层闪烁影响的卫星信号时,载噪比将会出现剧烈抖动,信噪比也会下降;更为严重的情况下,甚至将会导致卫星失锁的情况发生.
2) 建筑物遮挡相关脆弱性.城市中高楼林立,建筑物遮挡卫星信号,使接收机无法接收,对卫星信号形成物理上的阻塞.例如隧道中,卫星信号被完全频闭.
在城市峡谷等典型路段,多路径效应相当严重.即接收机接收到卫星信号时,所接收到的不仅是卫星信号,同时,还有经过多路径反射后再传播至接收机的卫星信号.当多路径效应相当严重时,伪距测量误差急剧增大,造成定位功能失效;此时,多路径效应从误差影响因素转变为脆弱性因素.
3) 电磁干扰相关脆弱性.城市中电磁环境复杂,存在严重的电磁干扰.
非故意干扰,来源可以是甚高频通信电台、GNSS频带带宽内的雷达系统,军用设备等.这些设备发出的电磁信号与卫星信号形成干涉,对卫星信号形成干扰; 故意干扰,即人为干扰.阻塞干扰时,即利用GNSS卫星信号功率低的特点,制造功率远大于卫星信号的同频率干扰信号,使卫星信号淹没于干扰信号中.欺骗干扰时,制造虚假卫星信号,发射虚假卫星电文,进而使GNSS功能失效.
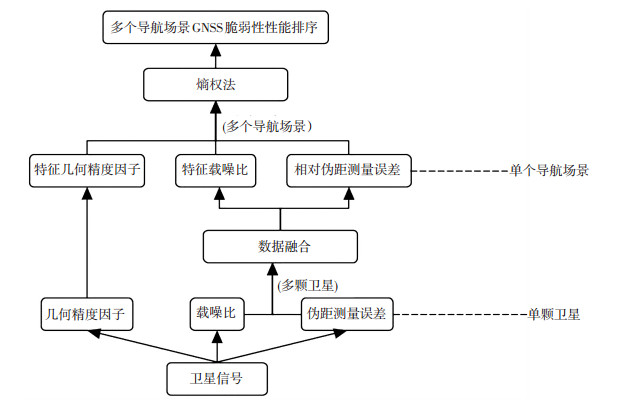
2 城市道路GNSS脆弱性评估系统本文采取的评估方式是:车辆携带设备在多个目标导航场景进行实地信号采集,利用实地采集到的接收机数据,采用数据融合算法对数据进行处理,最后评价多个导航场景GNSS脆弱性.评估框架如图 1所示,可分为:选取脆弱性评估指标,利用相对距离数据融合算法计算单个导航场景评估指标特征值,利用双基点数据融合算法计算多个导航场景脆弱性性能.
|
图 1 城市道路GNSS脆弱性评估框架 Figure 1 GNSS vulnerability assessment model of urban roads |
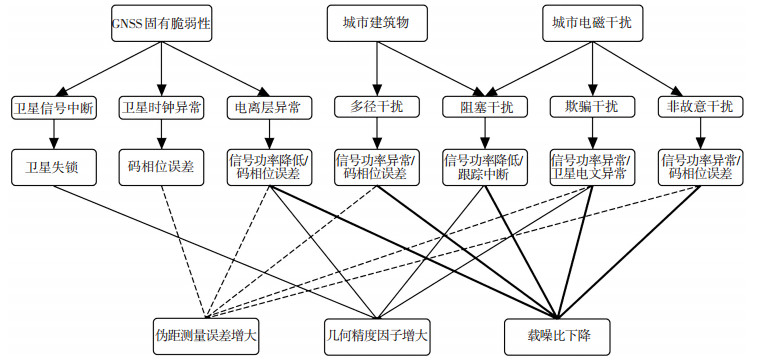
城市道路条件复杂,存在着诸如隧道、城市峡谷、林荫道等典型道路,对卫星信号产生遮挡.城市峡谷中的多路径效应相当严重,同时存在着大量的电磁干扰,降低卫星信号质量甚至频闭卫星信号.考虑到城市环境的特殊性,同时结合GNSS的固有脆弱性,本文选取载噪比、几何精度因子、伪距测量误差作为脆弱性评估指标,如图 2所示.
|
图 2 脆弱性因素与评估指标的关系 Figure 2 Relationship between vulnerability factors and indexes |
本文采用实际C/N0(carrier power to noise density ratio) 的计算方法.假设在累积间隔γ内,I、Q支路的采样值被划分M个区间,利用I/Q支路的相干积分结果计算带宽为M/γ的宽带功率PW和带宽为1/γ的窄带功率PN为:
| $ \begin{array}{*{20}{c}} {{P_W} = \left( {\sum\limits_i^M {\left( {I_{Pi}^2 + Q_{Pi}^2} \right)} } \right),}\\ {{P_N} = {{\left( {\sum\limits_i^M {{I_{Pi}}} } \right)}^2} + {{\left( {\sum\limits_i^M {{Q_{Pi}}} } \right)}^2}.} \end{array} $ |
通道内I、Q支路的相干积分IPi和QPi表示为:
| $ \begin{array}{l} {I_{Pi}} = \sqrt {2\left( {C/{N_0}} \right)\gamma /M} \cos \varphi + {w_{IPi}},\\ {Q_{Pi}} = \sqrt {2\left( {C/{N_0}} \right)\gamma /M} \sin \varphi + {w_{QPi}}. \end{array} $ |
式中:wIP、wQP分别为标准正态高斯噪声.为降低窄带功率和宽带功率的比值中噪声的影响,对测量值做n个时刻的平均:
| $ {{\bar P}_{N/W}} = \frac{1}{n}\sum\limits_{r = 1}^n {\frac{{{P_{Nr}}}}{{{P_{Wr}}}}} . $ |
由概率论可知C/N0与上述比例均值PN/W的关系为
| $ E\left( {{{\bar P}_{N/W}}} \right) = \frac{{M\left( {C/{N_0} \cdot \gamma + 1} \right)}}{{M + C/{N_0} \cdot \gamma }}, $ |
于是,以Hz为单位的C/N0计算公式为
| $ C/{N_0} = \frac{M}{\gamma }\frac{{{{\bar P}_{N/W}} - 1}}{{M - {{\bar P}_{N/W}}}}. $ |
导航学用精度因子DOP反应卫星布局的好坏.DOP决定测量误差在不同卫星布局时被放大的倍数.本文选取GDOP (几何精度因子) 反映卫星的几何分布.
接收机中的观测误差方程组为:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{H}} \cdot \mathit{\boldsymbol{\delta X}} = \mathit{\boldsymbol{L}},}\\ {\mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} { - {h_{11}}} & { - {h_{12}}} & { - {h_{13}}} & 1\\ { - {h_{21}}} & { - {h_{22}}} & { - {h_{23}}} & 1\\ \cdots & \cdots & \cdots & 1\\ { - {h_{n1}}} & { - {h_{n2}}} & { - {h_{n3}}} & 1 \end{array}} \right],}\\ {\mathit{\boldsymbol{\delta X}} = {{\left[ {\begin{array}{*{20}{c}} {\delta x} & {\delta y} & {\delta z} & {\delta {u_t}} \end{array}} \right]}^{\rm{T}}}.} \end{array} $ |
式中:H为观测矩阵;L为接收机测量伪距和卫星与接收机几何距离之差;hi1, hi2, hi3为用户到第i颗卫星的方向余弦;(δx, δy, δz) 为用户坐标修正值;δut为时钟误差.
将初始坐标X0代入观测误差方程组,迭代得到:
| $ \mathit{\boldsymbol{G}} = {\left( {{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{H}}} \right)^{ - 1}} = \left[ {\begin{array}{*{20}{c}} {{g_{11}}} & {{g_{12}}} & {{g_{13}}} & {{g_{14}}}\\ {{g_{21}}} & {{g_{22}}} & {{g_{23}}} & {{g_{24}}}\\ {{g_{31}}} & {{g_{32}}} & {{g_{33}}} & {{g_{34}}}\\ {{g_{41}}} & {{g_{42}}} & {{g_{43}}} & {{g_{44}}} \end{array}} \right], $ |
| $ \begin{array}{l} {\rm{GDOP = }}{\left( {{g_{11}} + {g_{22}} + {g_{33}} + {g_{44}}} \right)^{\frac{1}{2}}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;{\left( {\sigma _x^2 + \sigma _y^2 + \sigma _z^2 + \sigma _1^2} \right)^{\frac{1}{2}}}/\sigma = \\ \;\;\;\;\;\;\;\;\;\;\;\;{\left[ {{\rm{Trace}}{{\left( {G_u^{\rm{T}}{G_u}} \right)}^{ - 1}}} \right]^{1/2}} \end{array} $ |
伪距测量值与定位精度直接相关,在信号质量和卫星布局不变时,伪距测量误差越小,定位精度越高.定义单颗卫星的伪距测量误差Δρ为
| $ \Delta \rho = \left( {\rho - I - T - \Delta t} \right) - R. $ |
式中:ρ为软件接收机通过码相位得到的伪距测量值;I为电离层延时误差修正项;T为对流层延时误差修正项;Δt为接收机时钟误差修正项;R为卫星与监测站之间的真实距离.
本文中,利用自身精确定位和卫星星历计算真实距离R,文献[12]说明了差分GPS技术计算精确定位的方法.
2.2 导航场景特征参数计算每个导航场景中,交通用户依赖多颗卫星实现定位;接收机接收到每颗卫星的信号,均可计算此卫星的C/N0、Δρ.
取接收机接收到所有卫星定位解算时刻的数据段,计算GDOP、C/N0、Δρ,得到评估指标随时间变化的曲线.求平均值,得到导航场景GDOP特征值及每颗卫星的C/N0、Δρ.
现需要将多颗卫星的C/N0、Δρ科学地融合起来,得到最能反应导航场景特性的载噪比特征值CH_C/N0及相对伪距测量误差RPE.
以4颗卫星计算CH_C/N0为例 (GDOP特征值与RPE同理可得).将4颗卫星C/N0记为x1、x2、x3、x4.
测量两数据的相对距离为
| $ {d_{ij}} = \left| {{x_i} - {x_j}} \right|,\;\;\left( {i,j = 1,2,3,4} \right). $ |
定义隶属度函数:
| $ {r_{ij}} = 1 - \frac{{{d_{ij}}}}{{\max \left( {{d_{ij}}} \right)}}, $ |
可以看到,两数据越接近时,相对距离dij越小,隶属度函数rij越大,表示两者相互支持的程度越大,则两者在融合中所占的权重越大.那么,可以建立支持度矩阵:
| $ \mathit{\boldsymbol{R = }}\left( {\begin{array}{*{20}{c}} {{r_{12}}} & \cdots & {{r_{14}}}\\ \vdots & \ddots & \vdots \\ {{r_{41}}} & \cdots & {{r_{44}}} \end{array}} \right). $ |
由于矩阵R是非负的实对称矩阵,必存在非负的实特征值.设矩阵R最大模特征值为γ,对应的特征向量为
| $ \mathit{\boldsymbol{V = }}{\left( {\begin{array}{*{20}{c}} {{v_1}} & {{v_2}} & {{v_3}} & {{v_4}} \end{array}} \right)^{\rm{T}}}. $ |
文献[13]给出了各数据基于整体数据的权系数,可得特征载噪比为:
| $ \begin{array}{*{20}{c}} {{\omega _i} = \frac{{{v_i}}}{{\sum\limits_{i = 1}^4 {{v_i}} }},}\\ {CH\_C/{N_0} = \sum\limits_{i = 1}^4 {{\omega _i}{x_i}} .} \end{array} $ |
以3个典型交通导航场景为例开展评估.首先建立数据库:
| $ \mathit{\boldsymbol{X = }}\left( {\begin{array}{*{20}{c}} {{\rm{GDO}}{{\rm{P}}_1}} & {CH\_C/{N_{01}}} & {{\rm{RP}}{{\rm{E}}_1}}\\ {{\rm{GDO}}{{\rm{P}}_2}} & {CH\_C/{N_{02}}} & {{\rm{RP}}{{\rm{E}}_2}}\\ {{\rm{GDO}}{{\rm{P}}_3}} & {CH\_C/{N_{03}}} & {{\rm{RP}}{{\rm{E}}_3}} \end{array}} \right). $ |
将各个评价指标标准化,以GDOP为例:
| $ {\pi _i} = \frac{{{\rm{GDO}}{{\rm{P}}_i} - \min \left( {{\rm{GDOP}}} \right)}}{{\max \left( {{\rm{GDOP}}} \right) - \min \left( {{\rm{GDOP}}} \right)}}, $ |
可得到评估指标隶属度矩阵:R =(πij)3×3.文献[14]将热力学中“熵”的概念引入信息论,利用信息熵表示系统无序的程度.信息熵越大,则系统无序程度越小.定义一组指标的信息熵为
| $ {E_j} = - k\sum\limits_{i = 1}^n {\left( {{p_{ij}}\ln {p_{ij}}} \right)} . $ |
式中:
系统中,某个指标的信息熵越小,表示指标的变异程度越大,提供的信息量越大,在综合评价中所占的权重越大.文献[15]给出了熵权的计算方法:
| $ {w_i} = \frac{{1 - {E_i}}}{{3 - \sum\limits_{i = 1}^3 {{E_i}} }}. $ |
导航场景的载噪比特征值CH_C/N0反应了交通用户在该导航场景中接收到卫星信号的质量;几何精度因子特征值GDOP反应了接收机对卫星的观测误差对定位精度的影响;相对伪距测量误差RPE反应了接收机的测距误差对定位精度的影响.
由于3个评价指标从3个不同方面反应了GNSS的性能,若简单地乘以熵权相加,则无法准确评价GNSS脆弱性.所以,将不同导航场景的同一指标先进行比较,再结合各指标的熵权,可以更为准确地评价各导航场景GNSS脆弱性.
从各导航场景中,选取一组最优指标建立1套虚拟的正理想方案;选取一组最劣指标建立1套虚拟的负理想方案;再结合各指标的熵权,计算各实际导航场景距正、负理想方案的距离,从而更准确地比较各实际导航场景GNSS脆弱性的优劣.
由于GDOP、RPE越小,C/N0越大,GNSS性能越好;所以,选取最小的GDOP、RPE和最大的C/N0为正理想方案;选取最大的GDOP、RPE和最小的C/N0为负理想方案.结合各指标的熵权,计算实际方案距正、负理想方案的距离:
| $ \begin{array}{l} d_j^ + = \sum\limits_{i = 1}^3 {{w_i}\left| {{r_{ij}} - r_j^ + } \right|} ,\\ d_j^ - = \sum\limits_{i = 1}^3 {{w_i}\left| {{r_{ij}} - r_j^ - } \right|} , \end{array} $ |
式中,GDOP和RPE的rj+选取最小值,而C/N0的rj+则选取最大值.
距离正理想方案越近,则脆弱性性能越好;距离负理想方案越近,则脆弱性性能越差.
3 路测实验 3.1 典型城市道路 3.1.1 开阔路段开阔道路,指两侧均无遮挡的道路.开阔路段对卫星信号没有遮挡,接收机在开阔路段不仅可跟踪到10颗以上GPS卫星,而且参与定位解算的几何构型非常好,同时,信号质量不受影响.足够数量的卫星及优质的信号质量导致了GNSS良好的服务性能.
3.1.2 林荫道林荫道,指两侧有高大树木的道路.林荫道两侧的树木及树叶遮挡卫星信号,并且增强了多路径效应.由于卫星数量的减少及信号质量的略微降低,GNSS服务性能将略微降低.
3.1.3 城市峡谷城市峡谷,指道路两侧均有高度≥20 m的建筑物.由于高大建筑物对卫星信号的遮挡,接收机无法搜索到4颗卫星完成定位.并且,多路径效应严重,信号质量严重降低.城市峡谷中,GNSS服务性能严重降低.
3.1.4 隧道隧道中,卫星信号被完全阻隔.接收机无法搜索到卫星,GNSS服务性能瘫痪.
各城市道路条件可看作“不同类型”的特征道路或特征道路的“组合”.例如,高架桥下可视为另一“类型”的城市峡谷,对卫星信号的两侧遮挡转变为上方遮挡;一侧高楼、一侧高大树木的道路则可视为城市峡谷及林荫道的组合.
3.2 导航场景选取与卫星轨道参数选取导航场景与卫星星历见表 1.
| 表 1 主要导航场景信息 Table 1 Information of main scenes |
接收机捕获到9颗卫星,8颗用于定位解算.计算得到评估指标特征值,见表 2.
| 表 2 开阔路段评估指标特征值 Table 2 Characteristic value of vulnerability indexes in open road |
接收机捕获到6颗卫星,均用于定位解算,计算得到评估指标特征值,见表 3.
| 表 3 普通道路评估指标特征值 Table 3 Characteristic value of vulnerability indexes in common road |
接收机捕获到5颗卫星,均用于定位解算,计算得到评估指标征征值,见表 4.
| 表 4 林荫道评估指标特征值 Table 4 Characteristic value of vulnerability indexes in avenue |
接收机无法同时捕获到4颗卫星,无法完成定位.特征C/N0=0(dB·Hz),GDOP = 99.99(接收机软件上阈值),Δρ分别为:644.383 6、365.435 9、606.659 6、1 089.185 1 m.
3.3.5 隧道卫星信号被完全频闭,接收机无法捕获到卫星.特征C/N0=0(dB·Hz);GDOP = ∞,实际计算时取值99.99;Δρ= ∞,实际计算时,取值1 000 m,以近似正无穷.若取值过大,则使伪距测量误差在评估中所占权重过大而不切实际.
3.4 计算导航场景评估指标特征值由多种导航场景脆弱性评估,计算导航场景评估指标特征值,见表 5.
| 表 5 各导航场景特征指标 Table 5 Characteristic value of vulnerability indexes in all scenes |
由多种导航场景脆弱性评估,确定正、负理想方案,见表 6.同时,计算各场景距正、负理想方案距离,见表 7.
| 表 6 正负理想方案 Table 6 Positive and negative ideal schemes |
| 表 7 距正、负理想方案距离 Table 7 Distances to positive and negative ideal schemes |
1) 本文选择载噪比、几何精度因子、伪距测量误差作为脆弱性评价指标,采用基于信息熵权的数据融合算法,计算导航场景距正、负理想场景的距离,实现了多个导航场景的GNSS脆弱性评估.
2) 路测试验表明,开阔道路、林荫道、城市峡谷、隧道的GNSS脆弱性性能依次降低.本文算法可以完成城市道路GNSS脆弱性评估.
3) 普通道路的实验地点--万芳路两侧遮挡物较少,因此脆弱性情况较好.
4) 评价导航场景不同“时段”脆弱性,则需要在不同时段采集数据,然后利用本文算法评估脆弱性.
| [1] | VOLPE J A. Vulnerability assessment of the transportation infrastructure relying on the global positioning system[R].[S.l.]: NTSC NAVCEN draft report, 2001. |
| [2] | VAN DIERENDONCK A J. Eye on the ionosphere: measuring ionospheric scintillation effects from GPS signals[J]. GPS Solutions, 1999, 2(4): 60-63. DOI: 10.1007/PL00012769 |
| [3] | SKONE S, KNUDSEN K, DE JONG M. Limitations in GPS receiver tracking performance under ionospheric scintillation conditions[J]. Physics and Chemistry of the Earth, Part A: Solid Earth and Geodesy, 2001, 26(6/7/8): 613-621. DOI: 10.1016/S1464-1895(01)00110-7 |
| [4] | GE Linlin, HAN Shaowei, RIZOS C. Multipath mitigation of continuous GPS measurements using an adaptive filter[J]. GPS Solutions, 2000, 4(2): 19-30. DOI: 10.1007/PL00012838 |
| [5] | BRAASCH M S. Performance comparison of multipath mitigating receiver architectures[C]//Proceedings of the 2001 IEEE Aerospace Conference. Big Sky, MT: IEEE, 2001:31309-31505. DOI: 10.1109/AERO.2001.931361. |
| [6] | JAHROMI J A, BROUMANDAN A, NIELSEN J, et al. GPS spoofer countermeasure effectiveness based on signal strength, noise power, and C/N0 measurements[J]. International Journal of Satellite Communications and Networking, 2012, 30(4): 181-191. DOI: 10.1002/sat.1012 |
| [7] | ALEGRE F, AMEHRAYE A, EVANS N. A one-class classification approach to generalised speaker verification spoofing countermeasures using local binary patterns[C]//Proceedings of the 2013 IEEE Sixth International Conference on.Biometrics: Theory, Applications and Systems (BTAS). Washington, DC: IEEE, 2013: 1-8. DOI: 10.1109/BTAS.2013.6712706. |
| [8] | GUO Fei, ZHANG Xiaohong. Real-time clock jump compensation for precise point positioning[J]. GPS Solutions, 2014, 18(1): 41-50. DOI: 10.1007/s10291-012-0307-3 |
| [9] | LIU Xuan, ZHAN Xingqun, CHEN Maolin. Quantitative assessment of GNSS vulnerability based on DS evidence theory[J]. Journal of Aeronautics, Astronautics and Aviation, 2014, 46(3): 191-201. |
| [10] | JING Shuai, ZHAN Xingqun, LIU Xuan, et al. GNSS vulnerability assessment based on application suitability[C]//Proceedings of the 27th International Technical Meeting of The Satellite Division of the Institute of Navigation. Tampa, Florida: ION GNSS+ 2014, 2014: 2291-2298. |
| [11] |
严凯. GNSS脆弱性仿真评估平台技术研究[D]. 上海: 上海交通大学, 2013.
YAN Kai. Research on GNSS vulnerability simulation assessment platform technique[D]. Shanghai: Shanghai Jiao Tong University, 2013. |
| [12] | MORALES Y, TSUBOUCHI T. DGPS, RTK-GPS and Starfire DGPS performance under tree shading environments[C]//Proceedings of the IEEE International Conference on Integration Technology. Shenzhen: IEEE, 2007:519-524. DOI:10.1109/ICITECHNOLOGY.2007.4290370. |
| [13] |
KLEIN L A. 多传感器数据融合理论及应用[M]. 戴亚平, 刘征, 郁光辉, 译. 北京: 北京理工大学出版社, 2004: 47-56.
KLEIN L A. Multi-sensor data fusion theory and application[M]. DAI Yaping, LIU Zheng, YU Guanghui, T. Beijing: Beijing Institute of Technology Press, 2004:47-56. |
| [14] | ZHOU Jian, LI Xibing. Integrating unascertained measurement and information entropy theory to assess blastability of rock mass[J]. Journal of Central South University, 2012, 19(7): 1953-1960. DOI: 10.1007/s11771-012-1231-y |
| [15] |
孟宪萌, 胡和平. 基于熵权的集对分析模型在水质综合评价中的应用[J].
水利学报, 2009, 40(3): 257-263.
MENG Xianmeng, HU Heping. Application of set pair analysis model based on entropy weight to comprehensive evaluation of water quality[J]. Journal of Hydraulic Engineering, 2009, 40(3): 257-263. DOI: 10.3321/j.issn:0559-9350.2009.03.001 |
 2017, Vol. 49
2017, Vol. 49


