滞回非线性广泛存在于电磁、继电器、作动器、机电伺服等实际控制系统中^[1-5]，其表现出的多值性和不可微性严重影响被控系统的性能，甚至会造成系统不稳定^[6].近年来，许多学者^[7-10]针对此类非线性执行器的控制问题进行了广泛研究，并取得了一系列研究成果.

文献[7]利用自适应控制方法，针对受死区输入特性影响的非仿射非线性系统给出了控制器的设计方法，为解决存在滞回非线性输入特性的系统控制问题提供了有益借鉴.文献[8-9]针对一类存在Prandtl-Ishlinskii滞回输入的非线性系统提出了一种自适应动态面控制方法，有效补偿滞回非线性导致的系统不确定性的同时，动态面控制方法克服了Backstepping控制设计中存在“计算膨胀”的问题.文献[9]讨论了时滞非线性系统的自适应动态面控制器的设计问题.文献[10]通过Duhem模型对滞回非线性进行建模，设计了自适应动态面控制方案，简化了控制器复杂程度.文献[11]通过构造光滑的Backlash-like滞回及其逆的数学模型，基于自适应Backstepping控制设计了鲁棒控制器，克服了滞回非线性对系统的影响，但是控制器对滞回非线性的补偿误差依赖于其数学模型的精确程度.上述研究成果主要针对模型确定系统或是参数不确定性系统，且对滞回非线性模型施加了诸如逆存在、可微等限制条件.

本文针对一类具有非线性函数不确定和有界外界干扰的非线性系统，考虑非线性执行器发生未知故障的情况下，利用Backstepping滑模控制方法提出了一种鲁棒控制器设计方案.该方案建立了非线性执行器故障模型，包含了滞回非线性和失效、卡死等故障类型；利用RBF神经网络逼近系统的未知非线性函数项，RBF神经网络权值向量根据自适应律实时调整，保证了逼近效果；借鉴动态面控制思想，在Backstepping设计中引入一阶低通滤波器，避免了Backstepping控制器计算复杂性问题；利用改进的自适应滑模项有效补偿了系统不确定干扰的影响.通过理论分析，证明了系统输出能趋近于参考指令信号的邻域，仿真结果证明了该方案的有效性.

1 问题描述

考虑如下不确定非线性系统：

$ \left\{ \begin{array}{l} {{\dot x}_i} = {f_i}\left( {{{\mathit{\boldsymbol{\bar x}}}_i}} \right) + {x_{i + 1}} + {d_i}\left( {t,{\mathit{\boldsymbol{x}}_n}} \right),i = 1,2, \cdots ,n - 1;\\ {{\dot x}_n} = {f_n}\left( {{\mathit{\boldsymbol{x}}_n}} \right) + \sum\limits_{i = 1}^m {{b_i}\varphi \left( {{u_{ci}}} \right) + {d_n}\left( {t,{\mathit{\boldsymbol{x}}_n}} \right)} ;\\ y = {x_1}. \end{array} \right. $

(1)

式中：${{\boldsymbol{\bar{x}}}_{i}}={{[{{x}_{1}},\cdots ,{{x}_{i}}]}^{\text{T}}}\in {{\boldsymbol{R}}^{i}},{{\boldsymbol{x}}_{n}}={{[{{x}_{1}},\cdots ,{{x}_{n}}]}^{\text{T}}}\in {{\boldsymbol{R}}^{n}}$为系统状态向量；y∈R为系统输出；f_i(x_i)、f_n(x_n) 分别为未知光滑函数项；d_i(t, x_n)、d_n(t, x_n) 分别为系统未知不确定扰动项；b_i>0为未知控制增益；φ(u_ci) 为含有滞回非线性的执行器发生故障情况下的控制信号，其中u_ci为待设计输入控制信号.

本文对滞回非线性进行建模描述^[12]，其微分方程如下：

$ \frac{{{\rm{d}}{v_i}}}{{{\rm{d}}t}} = {A_i}\left| {\frac{{{\rm{d}}{u_{ci}}}}{{{\rm{d}}t}}} \right|\left( {{C_i}{u_{ci}} - {v_i}} \right) + {B_i}\frac{{{\rm{d}}{u_{ci}}}}{{{\rm{d}}t}},i = 1,2, \cdots ,m. $

(2)

式中：A_i、B_i、C_i分别为常数，且C_i>0，C_i>B_i；v_i为带有滞回非线性的执行器输出.

由式 (2) 可知：

$ {{v_i} = {C_i}{u_{ci}} + {{\bar d}_i}\left( {{u_{ci}}} \right),} $

(3)

$ \begin{array}{l} {{\bar d}_i}\left( {{u_i}} \right){\rm{ = }}\left( {{v_i}\left( 0 \right) - {C_i}{u_{ci}}\left( 0 \right)} \right){{\rm{e}}^{ - {A_i}\left( {{u_{ci}} - {u_{ci}}\left( 0 \right)} \right){\rm{sign}}\left( {{{\dot u}_{ci}}} \right)}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;{{\rm{e}}^{ - {A_i}{u_{ci}}{\rm{sign}}\left( {{{\dot u}_{ci}}} \right)}}\int_{{u_{ci}}\left( 0 \right)}^{{u_{ci}}} {\left( {{B_i} - {C_i}} \right){{\rm{e}}^{{A_i}\xi {\rm{sign}}\left( {{{\dot u}_{ci}}} \right)}}{\rm{d}}\xi } . \end{array} $

(4)

由此，滞回非线性可表示为线性部分C_iu_ci与非线性部分d_i(u_ci) 之和，且d_i(u_ci) 有界^{[10, 13]}.取B_i=3.163 5，C_i=0.345，当A_i=2, 3, 4, 5, 6时，带有滞回非线性执行器的输入输出关系如图 1所示.

假设第i个执行器在t_i时刻发生故障，t时刻 (t≥t_i) 执行器输出可表示为

$ \left\{ \begin{array}{l} \varphi \left( {{v_i}} \right) = {\rho _i}{v_i} + {u_{ki}},\\ {\rho _i}{u_{ki}} = 0. \end{array} \right. $

(5)

式中，0≤ρ_i≤1为执行器失效程度，u_ki为执行器发生卡死故障后固定输出.由此，式 (5) 可表示3类执行器状态：

(Ⅰ)ρ_i=1, u_ki=0，表示执行器正常工作，φ(v_i)=v_i；

(Ⅱ)0 < ρ_i < 1, u_ki=0，表示执行器部分失效，φ(v_i)=ρ_iv_i；

(Ⅲ)ρ_i=0，表示执行器完全失效，即卡死，φ(v_i)=u_ki.其中，u_ki=0表示一种特殊的卡死故障，即执行器卡死在0力矩位置，也可称为执行器松浮故障；u_ki=v_imax or v_imin表示执行器卡死在极限位置，也可称为执行器饱和故障.

综合式 (3) 和式 (5)，可知滞回非线性执行器不确定故障模型可表示如下：

$ \left\{ \begin{array}{l} \varphi \left( {{u_{ci}}} \right) = {\rho _i}{C_i}{u_{ci}} + {u_{ki}} + {\rho _i}{{\bar d}_i}\left( {{u_{ci}}} \right),\\ {\rho _i}{u_{ki}} = 0. \end{array} \right. $

(6)

式中d_i(u_ci) 有界.

由式 (1) 可知，系统模型可以表示如下：

$ \left\{ \begin{array}{l} {{\dot x}_i} = {f_i}\left( {{{\mathit{\boldsymbol{\bar x}}}_i}} \right) + {x_{i + 1}} + {d_i}\left( {t,{\mathit{\boldsymbol{x}}_n}} \right),\;\left( {i = 1,2, \cdots ,n - 1} \right);\\ {{\dot x}_n} = {f_n}\left( {{\mathit{\boldsymbol{x}}_n}} \right) + \sum\limits_{i = 1}^m {{b_i}\left( {{\rho _i}{C_i}{u_{ci}} + {u_{ki}}} \right)} + {{d'}_n}\left( {t,{\mathit{\boldsymbol{x}}_n}} \right);\\ y = {x_1}. \end{array} \right. $

(7)

式中，$d_{n}^{'}(t, {{\boldsymbol{x}}_{n}})={{d}_{n}}(t, {{\boldsymbol{x}}_{n}})+\sum\limits_{i=1}^{m}{{{b}_{i}}{{\rho }_{i}}{{{\bar{d}}}_{i}}({{u}_{ci}})}$.

假设1 执行器在一个工作周期内只发生一次故障，即由正常状态变为部分失效状态或由正常状态变为完全失效状态.且发生完全失效的执行器个数不超过m-1个.

假设2 未知不确定扰动项有界，即

$ \left| {{d_i}\left( {t,{\mathit{\boldsymbol{x}}_n}} \right)} \right| \le {D_i},\;\;i = 1,2, \cdots ,n - 1. $

注 由$d_{n}^{'}(t, {{\boldsymbol{x}}_{n}})={{d}_{n}}(t, {{\boldsymbol{x}}_{n}})+\sum\limits_{i=1}^{m}{{{b}_{i}}{{\rho }_{i}}{{{\bar{d}}}_{i}}({{u}_{ci}})}$和${{{\bar{d}}}_{i}}({{u}_{ci}})$有界可知，d_n^′(t, x_n) 有界，即|d_n^′(t, x_n)|≤D_n.

假设3 参考指令信号y_r及其n-1阶导数已知且有界.

设计RBF神经网络逼近系统中未知函数项，其表达式为

$ {h_{nn}}\left( Z \right) = {\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{\xi }}\left( \mathit{\boldsymbol{Z}} \right). $

式中：Z ∈ Ω_Z⊂ Rⁿ为输入向量；W = [W₁, …, W_l]^T∈ R^l为神经网络的权值向量，其中l为节点数；ξ(Z)=[ξ₁(Z), …, ξ_l(Z)]∈R^l是基函数向量.

引理1^[13] 对于任意连续函数h(Z)，存在RBF神经网络h_nn(Z)= W^*Tξ(Z) 使得

$ \mathop {\sup }\limits_{Z \in {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_Z}} \left| {h\left( \mathit{\boldsymbol{Z}} \right) - {h_{nn}}\left( \mathit{\boldsymbol{Z}} \right)} \right| \le {\varepsilon ^ * }. $

式中：ε^*>0；ε(Z)=h(Z)-h_nn(Z) 为神经网络的逼近误差. W^*为最优权值向量，取值为

$ {\mathit{\boldsymbol{W}}^ * } = \arg \mathop {\min }\limits_{\mathit{\boldsymbol{W}} \in {\mathit{\boldsymbol{R}}^l}} \left\{ {\mathop {\sup }\limits_{Z \in {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_Z}} \left| {h\left( \mathit{\boldsymbol{Z}} \right) - {\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{\xi }}\left( \mathit{\boldsymbol{Z}} \right)} \right|} \right\}. $

为提高系统对不确定性和未知干扰的鲁棒性，在控制器设计过程中引入滑模变结构控制项^[14].在Backstepping控制器推导过程中每一步骤要用到上一步骤虚拟控制函数的导数，且滑模控制的不连续易诱发高频抖振，本文采用以下一类连续可导的平滑函数代替滑模变结构控制中的符号函数：

$ g\left( x \right) = \frac{{1 - \exp \left( { - \eta x} \right)}}{{1 + \exp \left( { - \eta x} \right)}},\forall \eta > 0. $

引理2 ^[15] 对于η>0，x∈R，连续可导函数g(x) 满足如下不等式：

$ 0 \le \left| x \right| - x\frac{{1 - \exp \left( { - \eta x} \right)}}{{1 + \exp \left( { - \eta x} \right)}} \le \frac{1}{\eta }. $

针对不确定非线性系统 (7)，基于Backstepping滑模控制思想设计自适应鲁棒控制器，有效补偿系统不确定性、滞回非线性以及执行器未知故障的影响，使得系统输出信号跟踪参考指令信号，且闭环系统所有信号半全局最终有界.

2 控制器设计及稳定性分析

定义闭环系统跟踪误差为：

$ \begin{array}{l} {e_1} = {x_1} - {y_r},\\ {e_i} = {x_i} - {\alpha _{i - 1}},i = 2, \cdots ,n. \end{array} $

(8)

式中e₁为系统跟踪误差，α_i-1为第i-1阶子系统的期望虚拟控制信号.

Step 1 由闭环系统 (7) 可知，系统跟踪误差e₁的导数为

$ {{\dot e}_1} = {f_1}\left( {{x_1}} \right) + {x_2} + {d_1} - {{\dot y}_r}. $

采用自适应RBF神经网络逼近系统未知非线性函数项f₁(x₁)，对于紧集Ω⊂R，存在最优权值向量W₁^*，有

$ {f_1}\left( {{x_1}} \right) = \mathit{\boldsymbol{W}}_1^{ * {\rm{T}}}{\mathit{\boldsymbol{\xi }}_1}\left( {{x_1}} \right) + {\varepsilon _1}, $

式中ε₁为逼近误差，|ε₁|≤ε₁^*.取

$ {{\mathit{\boldsymbol{\tilde W}}}_1} = \mathit{\boldsymbol{W}}_1^ * - {{\mathit{\boldsymbol{\hat W}}}_1}. $

式中, $\boldsymbol{\hat{W}}$为神经网络最优权值的估计值，$\boldsymbol{\hat{W}}$为估计误差.神经网络权值向量的自适应律取为

$ {{{\mathit{\boldsymbol{\dot{\hat{W}}}}}}_{1}} = {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_1}{\xi _1}\left( {{x_1}} \right){e_1}, $

(9)

式中Γ₁= Γ₁^T>0为自适应增益矩阵.

定义边界值D₁^′=D₁+ε₁^*，设计自适应律对D₁^′进行估计:

$ {{{\dot{\hat{D}}}}_{1}} = {\gamma _1}\left| {{e_1}} \right|, $

(10)

式中γ₁为自适应增益系数.估计误差为${{\tilde{D}}_{1}}=D_{1}^{'}-{{\hat{D}}_{1}}$.

选择切换函数s₁=e₁，则可设计在不考虑e₂时的自适应变结构虚拟控制律为

$ {{\alpha '}_1} = - {k_1}{e_1} - \mathit{\boldsymbol{\hat W}}_1^{\rm{T}}{\mathit{\boldsymbol{\xi }}_1}\left( {{x_1}} \right) - {{\hat D}_1}\frac{{1 - \exp \left( { - {\eta _1}{{\hat D}_1}{e_1}} \right)}}{{1 + \exp \left( { - {\eta _1}{{\hat D}_1}{e_1}} \right)}} + {{\dot y}_r}, $

(11)

式中η₁>0，k₁>0为设计参数.

借鉴动态面控制思想，为避免Backstepping推导过程中对虚拟控制信号反复求导带来的“计算膨胀”问题，引入一阶低通滤波器对虚拟信号进行滤波处理，简化了虚拟信号导数求解的过程.滤波器动态方程如下:

$ {\tau _1}{{\dot \alpha }_1} + {\alpha _1} = {{\alpha '}_1},{\alpha _1}\left( 0 \right) = {{\alpha '}_1}\left( 0 \right), $

式中τ₁>0为滤波器时间常数.则虚拟控制的导数可表示为

$ {{\dot \alpha }_1} = - \frac{{{\alpha _1} - {{\alpha '}_1}}}{{{\tau _1}}} = - \frac{{{\omega _1}}}{{{\tau _1}}}, $

式中ω₁=α₁-α₁^′为第1阶子系统的边界层误差.

定义Lyapunov函数为

$ {V_1} = \frac{1}{2}e_1^2 + \frac{1}{2}\mathit{\boldsymbol{\tilde W}}_1^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_1^{ - 1}{{\mathit{\boldsymbol{\tilde W}}}_1} + \frac{1}{{2{\gamma _1}}}\tilde D_1^2, $

对V₁按时间t求得

$ {{\dot V}_1} = {e_1}{{\dot e}_1} - \mathit{\boldsymbol{\tilde W}}_1^{\rm{T}}\mathit{\Gamma }_{\rm{1}}^{{\rm{ - 1}}}{{{\mathit{\boldsymbol{\dot{\hat{W}}}}}}_{1}} - \frac{{\rm{1}}}{{{\gamma _{\rm{1}}}}}{{\mathit{\tilde D}}_{\rm{1}}}{{{\dot{\hat{D}}}}_{1}}. $

在自适应律 (9)、(10) 和虚拟控制律 (11) 的作用下，V₁按时间t求导得

$ \begin{array}{l} {{\dot V}_1} = {e_1}{{\dot e}_1} - \mathit{\boldsymbol{\tilde W}}_1^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_1^{ - 1}{{{\mathit{\boldsymbol{\dot{\hat{W}}}}}}_{1}} - \frac{1}{{{\gamma _1}}}{{\tilde D}_1}{{{\dot{\hat{D}}}}_{1}} \le \\ \;\;\;\;\;\; - {k_1}e_1^2 + {e_1}{e_2} - \mathit{\boldsymbol{\tilde W}}_1^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_1^{ - 1}\left( {{{{\mathit{\boldsymbol{\dot{\hat{W}}}}}}_{1}} - {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_1}{\xi _1}\left( {{x_1}} \right){e_1}} \right) + \\ \;\;\;\;\;\;\left| {{e_1}} \right|{{\hat D}_1} - {e_1}{{\hat D}_1}\frac{{1 - \exp \left( { - {\eta _1}{{\hat D}_1}{e_1}} \right)}}{{1 + \exp \left( { - {\eta _1}{{\hat D}_1}{e_1}} \right)}} - \\ \;\;\;\;\;\;\frac{1}{{{\gamma _1}}}{{\tilde D}_1}\left( {{{{\dot{\hat{D}}}}_{1}} - {\gamma _1}\left| {{e_1}} \right|} \right) \le - {k_1}e_1^2 + {e_1}{e_2} + \\ \;\;\;\;\;\;\left| {{e_1}} \right|{{\hat D}_1} - {e_1}{{\hat D}_1}\frac{{1 - \exp \left( { - {\eta _1}{{\hat D}_1}{e_1}} \right)}}{{1 + \exp \left( { - {\eta _1}{{\hat D}_1}{e_1}} \right)}}. \end{array} $

由引理2可知：

$ {{\dot V}_1} \le - {k_1}e_1^2 + {e_1}{e_2} + \frac{1}{{{\eta _1}}}. $

Step i 第i阶子系统跟踪误差e_i的导数为

$ {{\dot e}_i} = {f_i}\left( {{{\mathit{\boldsymbol{\bar x}}}_i}} \right) + {x_{i + 1}} + {d_i} - {{\dot \alpha }_{i - 1}}. $

类似地，选择切换函数s_i=e_i，可设计如下虚拟控制律:

$ \begin{array}{l} {{\alpha '}_i} = - {k_i}{e_i} - {e_{i - 1}} - \mathit{\boldsymbol{\hat W}}_i^{\rm{T}}{\mathit{\boldsymbol{\xi }}_i}\left( {{{\mathit{\boldsymbol{\bar x}}}_i}} \right) - \\ \;\;\;\;\;\;\;{{\hat D}_i}\frac{{1 - \exp \left( { - {\eta _i}{{\hat D}_i}{e_i}} \right)}}{{1 + \exp \left( { - {\eta _i}{{\hat D}_i}{e_i}} \right)}} + {{\dot \alpha }_{i - 1}}, \end{array} $

式中η_i>0，k_i>0为待设计参数.

应用RBF神经网络逼近系统中未知函数项f_i(x_i)：对于紧集Ω_i⊂Rⁱ，有

$ {f_i}\left( {{{\mathit{\boldsymbol{\bar x}}}_i}} \right) = \mathit{\boldsymbol{\hat W}}_i^{\rm{T}}{\mathit{\boldsymbol{\xi }}_i}\left( {{{\mathit{\boldsymbol{\bar x}}}_i}} \right) + \mathit{\boldsymbol{\tilde W}}_i^{\rm{T}}{\mathit{\boldsymbol{\xi }}_i}\left( {{{\mathit{\boldsymbol{\bar x}}}_i}} \right) + {\varepsilon _i}. $

式中，${{\boldsymbol{\hat{W}}}_{i}}$为最优权值的估计值，估计误差为${{\boldsymbol{\hat{W}}}_{i}}=\boldsymbol{W}_{i}^{*}-{{\boldsymbol{\hat{W}}}_{i}}$.自适应律取为

$ {{{\mathit{\boldsymbol{\dot{\hat{W}}}}}}_{i}} = {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_i}{\xi _i}\left( {{{\mathit{\boldsymbol{\bar x}}}_i}} \right){e_i}, $

(12)

式中Γ_i= Γ_i^T>0为自适应增益矩阵.根据引理1可知，神经网络逼近误差满足|ε_i|≤ε_i^*.定义边界值D_i^′=D_i+ε_i^*，设计自适应律对边界值D_i^′进行估计:

$ {{{\dot{\hat{D}}}}_{i}} = {\gamma _i}\left| {{e_i}} \right|, $

(13)

式中γ_i为自适应增益系数.其中，${{\hat{D}}_{i}}$为边界值的估计值，估计误差为${{\tilde{D}}_{i}}=D_{i}^{'}-{{\hat{D}}_{i}}$.

在第i-1阶子系统，采用动态面控制得到虚拟控制的导数为

$ {{\dot \alpha }_{i - 1}} = - \frac{{{\omega _{i - 1}}}}{{{\tau _{i - 1}}}}, $

由此，第i阶子系统虚拟控制取为

$ \begin{array}{l} {{\alpha '}_i} = - {k_i}{e_i} - {e_{i - 1}} - \mathit{\boldsymbol{\hat W}}_i^{\rm{T}}{\mathit{\boldsymbol{\xi }}_i}\left( {{{\mathit{\boldsymbol{\bar x}}}_i}} \right) - \\ \;\;\;\;\;\;{{\hat D}_i}\frac{{1 - \exp \left( { - \eta {{\hat D}_i}{e_1}} \right)}}{{1 + \exp \left( { - \eta {{\hat D}_i}{e_1}} \right)}} - \frac{{{\omega _{i - 1}}}}{{{\tau _{i - 1}}}}. \end{array} $

定义Lyapunov函数为

$ {V_i} = {V_{i - 1}} + \frac{1}{2}e_i^2 + \frac{1}{2}\mathit{\boldsymbol{\tilde W}}_i^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_1^{ - 1}{{\mathit{\boldsymbol{\tilde W}}}_i} + \frac{1}{{2{\gamma _i}}}\tilde D_i^2. $

在虚拟控制律 (12) 和自适应律 (13) 的作用下，容易导出V_i按时间t的导数为

$ {{\dot V}_i} \le - \sum\limits_{j = 1}^i {{k_j}e_j^2 + {e_i}{e_{i + 1}}} + \sum\limits_{j = 1}^i {\frac{1}{{{\eta _j}}}} ,i = 1,2, \cdots ,n - 1. $

(14)

Step n 第n阶子系统跟踪误差e_n的导数为

$ \begin{array}{l} {{\dot e}_n} = {f_n}\left( {{x_n}} \right) + \sum\limits_{i = 1}^m {{b_i}\left( {{\rho _i}{C_i}{u_{ci}} + {u_{ki}}} \right)} + {{d'}_n} - {{\dot \alpha }_{n - 1}} = \\ \;\;\;\;\;\;\;\;{f_n}\left( {{x_n}} \right) + \sum\limits_{i = 1}^m {{b_i}\left( {{\rho _i}{C_i}{u_{ci}} + {u_{ki}}} \right)} + {{d'}_n} + \frac{{{\omega _{n - 1}}}}{{{\tau _{n - 1}}}}. \end{array} $

可设计第n阶子系统虚拟控制律和自适应律为:

$ \begin{array}{l} {\alpha _n} = - {k_n}{e_n} - {e_{n - 1}} - \mathit{\boldsymbol{\hat W}}_n^{\rm{T}}{\mathit{\boldsymbol{\xi }}_n}\left( {{\mathit{\boldsymbol{x}}_n}} \right) - \\ \;\;\;\;\;\;\;{{\hat D}_n}\frac{{1 - \exp \left( { - {\eta _n}{{\hat D}_n}{e_n}} \right)}}{{1 + \exp \left( { - {\eta _n}{{\hat D}_n}{e_n}} \right)}} - \frac{{{\omega _{n - 1}}}}{{{\tau _{n - 1}}}}, \end{array} $

(15)

$ {{{\mathit{\boldsymbol{\dot{\hat{W}}}}}}_{n}} = {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_n}{\xi _n}\left( {{x_n}} \right){e_n}, $

(16)

$ {{{\dot{\hat{D}}}}_{n}}={{\gamma }_{n}}\left| {{e}_{n}} \right|. $

(17)

式中: ${{\boldsymbol{\hat{W}}}_{n}}$为最优权值W_n^*的自适应估计值，估计误差为${{\boldsymbol{\tilde{W}}}_{n}}=\boldsymbol{W}_{n}^{*}-{{\boldsymbol{\hat{W}}}_{n}}$; ${{{\hat{D}}}_{n}}$为边界值D_n^′=D_n+ε_n的估计值，估计误差为${{{\tilde{D}}}_{n}}=D_{n}^{'}-{{{\hat{D}}}_{n}}$; Γ_n= Γ_n^T>0为自适应增益矩阵; γ_n为自适应增益系数，η_n>0，k_n>0为待设计参数.

由第n阶子系统动态方程可知：

$ \sum\limits_{i = 1}^m {{b_i}\left( {{\rho _i}{C_i}{u_{ci}} + {u_{ki}}} \right)} = {\alpha _n}, $

(18)

式中u_ci即为最终待设计输入控制律.

根据故障模型 (6)，C_i，u_ki和ρ_i均为未知参数，故障参数u_ki和ρ_i随着故障类型及发生故障执行器数量的变化而变化.设计如下自适应控制律:

$ {u_{ci}} = {{\mathit{\boldsymbol{\hat P}}}^{\rm{T}}}\mathit{\boldsymbol{Q}}, $

(19)

其中Q为m+1维已知参数向量，取为

$ \mathit{\boldsymbol{Q = }}{\left( {{Q_1},{Q_2}, \cdots ,{Q_{m + 1}}} \right)^{\rm{T}}} = {\left( {{\alpha _n},1, \cdots ,1} \right)^{\rm{T}}}, $

P为描述系统未知非线性和未知执行器故障情况的参数向量，设计自适应律估计其真实值，自适应律取为

$ {\dot{\hat{P}}} = {\left( {{P_1},{P_2}, \cdots ,{P_{m + 1}}} \right)^{\rm{T}}} = - {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_P}\mathit{\boldsymbol{Q}}{e_n}, $

(20)

式中Γ_P= Γ_P^T>0为自适应增益矩阵

定理1 考虑由状态方程 (1)，具有滞回非线性特性执行器 (2)，执行器未知故障模型 (5) 组成的不确定非线性闭环系统，在假设1~3条件下，基于Backstepping变结构原理设计的控制律 (18) 和自适应律 (17)、(20)，能够使得系统输出跟踪参考指令信号，且闭环系统所有信号半全局一致最终有界.

证明 根据假设2，假定在T₁, T₂, …, T_f时刻发生故障的执行器的个数分别为p₁, p₂, …, p_f，其中，$\sum\limits_{i=1}^{f}{{{p}_{i}}\le m-1}$.而在时间区间[T₀, T₁), (T₁, T₂), …, (T_f, ∞) 中则没有故障出现.即在时间区间[T_j, T_j+1) 中故障集中发生在时刻T_j.用M_j表示在时刻T_j完全失效执行器集合，M_j表示正常和部分失效执行器的集合.则M_j∪M_j={1, 2, …, m}.根据未知故障模型 (6)，可知

$ \left\{ \begin{array}{l} {\rho _i} = 0,i \in {{\bar M}_j};\\ 0 < {\rho _i} \le 1,i \in {M_j}. \end{array} \right. $

式中i=1, 2, …, m.

在时间区间[T₀, T₁) 内，定义如下Lyapunov函数:

$ \begin{array}{l} {V_{n0}} = {V_{n - 1}} + \frac{1}{2}e_n^2 + \frac{1}{2}\mathit{\boldsymbol{\tilde W}}_n^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_n^{ - 1}{{\mathit{\boldsymbol{\tilde W}}}_n} + \frac{1}{{2{\gamma _n}}}\tilde D_n^2 + \\ \;\;\;\;\;\;\;\frac{1}{2}\sum\limits_{i = 1}^m {{b_i}{C_i}{{\mathit{\boldsymbol{\tilde P}}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_n^{ - 1}\mathit{\boldsymbol{\tilde P}}} , \end{array} $

式中$\boldsymbol{\tilde{P}}=\boldsymbol{P}-\boldsymbol{\hat{P}}$.

V_n0按时间t的导数为

$ \begin{array}{l} {{\dot V}_{n0}} = {{\dot V}_{n - 1}} + {e_n}{{\dot e}_n} - \mathit{\boldsymbol{\tilde W}}_n^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_n^{ - 1}{{{\mathit{\boldsymbol{\dot{\hat{W}}}}}}_{n}} - \frac{1}{{{\gamma _n}}}{{\tilde D}_n}{{{\dot{\hat{D}}}}_{n}} - \\ \;\;\;\;\;\;\;\;\sum\limits_{i = 1}^m {{b_i}{C_i}{{\mathit{\boldsymbol{\tilde P}}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_p^{ - 1}{\mathit{\boldsymbol{\dot{\hat{P}}}}}} . \end{array} $

在[T₀, T₁) 内没有故障发生，即ρ_i=1, u_ki=0，可知：

$ \begin{array}{l} \sum\limits_{i = 1}^m {{b_i}\left( {{\rho _i}{C_i}{u_{ci}} + {u_{ki}}} \right)} = \sum\limits_{i = 1}^m {{b_i}{C_i}{\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{Q}}} - \sum\limits_{i = 1}^m {{b_i}{C_i}{{\mathit{\boldsymbol{\tilde P}}}^{\rm{T}}}\mathit{\boldsymbol{Q}}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\alpha _n} - \sum\limits_{i = 1}^m {{b_i}{C_i}{{\mathit{\boldsymbol{\tilde P}}}^{\rm{T}}}\mathit{\boldsymbol{Q}}} . \end{array} $

由自适应律 (20) 和虚拟控制表达式 (17) 可知，e_n的导数可重写为

$ \begin{array}{l} {{\dot e}_n} = {f_n}\left( {{\mathit{\boldsymbol{x}}_n}} \right) + \sum\limits_{i = 1}^m {{b_i}{C_i}{u_{ci}}} + {{d'}_n} + \frac{{{\omega _{n - 1}}}}{{{\tau _{n - 1}}}} = \\ \;\;\;\;\;\;\; - {k_n}{e_n} - {e_{n - 1}} + \mathit{\boldsymbol{\tilde W}}_n^{\rm{T}}{\mathit{\boldsymbol{\xi }}_n}\left( {{\mathit{\boldsymbol{x}}_n}} \right) - \\ \;\;\;\;\;\;\;{{\hat D}_n}\frac{{1 - \exp \left( { - {\eta _n}{{\hat D}_n}{e_n}} \right)}}{{1 + \exp \left( { - {\eta _n}{{\hat D}_n}{e_n}} \right)}} - \sum\limits_{i = 1}^m {{b_i}{C_i}{{\mathit{\boldsymbol{\tilde P}}}^{\rm{T}}}\mathit{\boldsymbol{Q}}} + {{d'}_n}. \end{array} $

由式 (14)，自适应律 (17) 和引理1，可以得到:

$ \begin{array}{l} {{\dot V}_{n0}} = {{\dot V}_{n - 1}} + {e_n}{{\dot e}_n} - \mathit{\boldsymbol{\tilde W}}_n^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_n^{ - 1}{{{\mathit{\boldsymbol{\dot{\hat{W}}}}}}_{n}} - \frac{1}{{{\gamma _n}}}{{\tilde D}_n}{{{\dot{\hat{D}}}}_{n}} - \\ \;\;\;\;\;\;\;\;\sum\limits_{i = 1}^m {{b_i}{C_i}{{\mathit{\boldsymbol{\tilde P}}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_p^{ - 1}{\mathit{\boldsymbol{\dot{\hat{P}}}}}} \le - \sum\limits_{i = 1}^n {{k_i}e_i^2} + \sum\limits_{i = 1}^{n - 1} {\frac{1}{{{\eta _i}}}} + \\ \;\;\;\;\;\;\;\;\mathit{\boldsymbol{\tilde W}}_n^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_n^{ - 1}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_n}{\mathit{\boldsymbol{\xi }}_n}\left( {{\mathit{\boldsymbol{x}}_n}} \right){e_n} - {{{\mathit{\boldsymbol{\dot{\hat{W}}}}}}_{n}}} \right) + \\ \;\;\;\;\;\;\;\;\;\left( {\left| {{e_n}} \right|{{\hat D}_n} - {e_n}{{\hat D}_n}\frac{{1 - \exp \left( { - {\eta _n}{{\hat D}_n}{e_n}} \right)}}{{1 + \exp \left( { - {\eta _n}{{\hat D}_n}{e_n}} \right)}}} \right) - \\ \;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^m {{b_i}{C_i}{{\mathit{\boldsymbol{\tilde P}}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_p^{ - 1}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_P}\mathit{\boldsymbol{Q}}{e_n}\mathit{\boldsymbol{ + }}{\mathit{\boldsymbol{\dot{\hat{P}}}}}} \right)} + \\ \;\;\;\;\;\;\;\;\;\frac{1}{{{\gamma _n}}}{{\tilde D}_n}\left( {{\gamma _n}\left| {{e_n}} \right| - {{{\dot{\hat{D}}}}_{n}}} \right) \le - \sum\limits_{i = 1}^n {{k_i}e_i^2} + \\ \;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^n {\frac{1}{{{\eta _i}}}} - \sum\limits_{i = 1}^m {{b_i}{C_i}{{\mathit{\boldsymbol{\tilde P}}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_p^{ - 1}\left( {{\mathit{\Gamma }_P}\mathit{\boldsymbol{Q}}{e_n}\mathit{\boldsymbol{ + }}{\mathit{\boldsymbol{\dot{\hat{P}}}}}} \right)} . \end{array} $

(21)

将自适应律 (17) 代入得

$ {{{\dot{V}}}_{n0}}\le -\sum\limits_{i=1}^{n}{{{k}_{i}}e_{i}^{2}}+\sum\limits_{i=1}^{n}{\frac{1}{{{\eta }_{i}}}}. $

取η_i=exp (t), i=1, 2, …, n，即$\underset{t\to \infty }{\mathop{\lim }}\, (\sum\limits_{i=1}^{n}{\frac{1}{{{\eta }_{i}}}})=0$.可知在时间区间[T₀, T₁) 内，V_n0(t) 有界.由此，在[T₀, T₁) 内，闭环系统所有信号e_i, ${{{\boldsymbol{\tilde{W}}}}_{i}}, {{{\tilde{D}}}_{i}}{{{\boldsymbol{\tilde{P}}}}_{i}}$全局一致最终有界.

根据分析，在时刻T₁有p₁个执行器发生故障，且在时间区间T₁, T₂无故障发生.在T₁, T₂内，定义如下Lyapunov函数：

$ \begin{array}{*{20}{l}} {{V_{n1}} = {V_{n - 1}} + \frac{1}{2}e_n^2 + \frac{1}{2}\mathit{\boldsymbol{\tilde W}}_n^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_n^{ - 1}{{\mathit{\boldsymbol{\tilde W}}}_n} + \frac{1}{{2{\gamma _n}}}\tilde D_n^2 + }\\ {\;\;\;\;\;\;\;\frac{1}{2}\sum\limits_{i = {M_1}}^m {{b_i}{\rho _i}{C_i}{{\mathit{\boldsymbol{\tilde P}}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_n^{ - 1}\mathit{\boldsymbol{\tilde P}}} .} \end{array} $

由式 (18) 可知

$ \begin{array}{*{20}{l}} {\sum\limits_{i = 1}^m {{b_i}\left( {{\rho _i}{C_i}{u_{ci}} + {u_{ki}}} \right)} = \sum\limits_{i = {M_1}}^m {{b_i}{\rho _i}{C_i}{\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{Q}} - \sum\limits_{i = {M_1}}^m {{b_i}{\rho _i}{C_i}{{\mathit{\boldsymbol{\tilde P}}}^{\rm{T}}}\mathit{Q}} + }\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = {{\bar M}_1}}^m {{b_i}{u_{ki}}} = {\alpha _n} - \sum\limits_{i = {M_1}}^m {{b_i}{\rho _i}{C_i}{{\mathit{\boldsymbol{\tilde P}}}^{\rm{T}}}\mathit{Q}} .} \end{array} $

由式 (17)，(18) 和自适应律 (20) 可知，e_n的导数为

$ \begin{array}{*{20}{l}} {{{\dot e}_n} = {f_n}\left( {{\mathit{\boldsymbol{x}}_n}} \right) + \sum\limits_{i = 1}^m {{b_i}} \left( {{\rho _i}{C_i}{u_{ci}} + {u_{ki}}} \right) + {{d'}_n} + \frac{{{\omega _{n - 1}}}}{{{\tau _{n - 1}}}} = }\\ {\;\;\;\;\;\;\; - {k_n}{e_n} - {e_{n - 1}} + \mathit{\tilde W}_n^{\rm{T}}{\mathit{\xi }_n}\left( {{\mathit{x}_n}} \right) - }\\ {\;\;\;\;\;\;\;{{\hat D}_n}\frac{{1 - \exp \left( { - {\eta _n}{{\hat D}_n}{e_n}} \right)}}{{1 + \exp \left( { - {\eta _n}{{\hat D}_n}{e_n}} \right)}} - \sum\limits_{i = {M_1}}^m {{b_i}{\rho _i}{C_i}{{\mathit{\boldsymbol{\tilde P}}}^{\rm{T}}}\mathit{Q}} + {{d'}_n}.} \end{array} $

由式 (14)，自适应律 (17) 和引理1，可以得到:

$ \begin{array}{*{20}{l}} {{{\dot V}_{n1}} = {{\dot V}_{n - 1}} + {e_n}{{\dot e}_n} - \mathit{\boldsymbol{\tilde W}}_n^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_n^{ - 1}{{{\mathit{\boldsymbol{\dot{\hat{W}}}}}}_{n}} - \frac{1}{{{\gamma _n}}}{{\tilde D}_n}{{{\dot{\hat{D}}}}_{n}} - }\\ {\;\;\;\;\;\;\;\;\sum\limits_{i = {M_1}}^m {{b_i}{\rho _i}{C_i}{{\mathit{\boldsymbol{\tilde P}}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_p^{ - 1}} {\mathit{\boldsymbol{\dot{\hat{P}}}}} \le - \sum\limits_{i = 1}^n {{k_i}e_i^2} + \sum\limits_{i = 1}^{n - 1} {\frac{1}{{{\eta _i}}}} + }\\ {\;\;\;\;\;\;\;\;\mathit{\boldsymbol{\tilde W}}_n^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_n^{ - 1}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_n}{\mathit{\boldsymbol{\xi }}_n}\left( {{\mathit{\boldsymbol{x}}_n}} \right){e_n} - {{{\mathit{\boldsymbol{\dot{\hat{W}}}}}}_{n}}} \right) + }\\ {\;\;\;\;\;\;\;\;\;\left( {\left| {{e_n}} \right|{{\hat D}_n} - {e_n}{{\hat D}_n}\frac{{1 - \exp \left( { - {\eta _n}{{\hat D}_n}{e_n}} \right)}}{{1 + \exp \left( { - {\eta _n}{{\hat D}_n}{e_n}} \right)}}} \right) - }\\ {\;\;\;\;\;\;\;\;\;\sum\limits_{i = {M_1}}^m {{b_i}{\rho _i}{C_i}{{\mathit{\boldsymbol{\tilde P}}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_p^{ - 1}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_P}\mathit{\boldsymbol{Q}}{e_n} + {\mathit{\boldsymbol{\dot{\hat{P}}}}}} \right)} + }\\ {\;\;\;\;\;\;\;\;\;\frac{1}{{{\gamma _n}}}{{\tilde D}_n}\left( {{\gamma _n}\left| {{e_n}} \right| - {{{\dot{\hat{D}}}}_{n}}} \right) \le - \sum\limits_{i = 1}^n {{k_i}e_i^2} + \sum\limits_{i = 1}^n {\frac{1}{{{\eta _i}}}} - }\\ {\;\;\;\;\;\;\;\;\;\sum\limits_{i = {M_1}}^m {{b_i}{\rho _i}{C_i}{{\mathit{\boldsymbol{\tilde P}}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_p^{ - 1}\left( {{\mathit{\Gamma }_P}\mathit{\boldsymbol{Q}}{e_n} + {\mathit{\boldsymbol{\dot{\hat{P}}}}}} \right)} .} \end{array} $

(22)

将自适应律 (20) 代入得

$ {{\dot V}_{n1}} \le - \sum\limits_{i = 1}^n {{k_i}e_i^2} + \sum\limits_{i = 1}^n {\frac{1}{{{\eta _i}}}} . $

(23)

可知在时间区间 (T₁, T₂) 内，V_n1(t) 有界.由此，在 (T₁, T₂) 内，闭环系统所有信号e_i, ${{{\boldsymbol{\tilde{W}}}}_{i}}, {{{\tilde{D}}}_{i}}{{{\boldsymbol{\tilde{P}}}}_{i}}$半全局一致最终有界.

注 比较式 (21)、(22)，V_n0(T₁^-) 和V_n1(T₁⁺) 只存在误差项${\boldsymbol{\tilde{P}}}$Γ_p^-1${\boldsymbol{\tilde{P}}}$系数的不同.由执行器故障模型和假设2可知，在执行器故障出现时，输出控制信号${{u}_{ci}}={{{\boldsymbol{\hat{P}}}}^{\text{T}}}\boldsymbol{Q}$的跳变是有界的，故V_n0(T₁^-) 和V_n1(T₁⁺) 均有界.

同理，可得V_n2(t), …, V_nf(t) 在时间区间 (T₂, T₃), …, (T_f, ∞) 有界，且V_n1(T₂^-), V_n2(T₂⁺), V_n2(T₃^-), …, V_n(f-1)(T_f-1^-), V_nf(T_f⁺) 均有界.由此，可推得闭环系统所有信号e_i, ${{{\boldsymbol{\tilde{W}}}}_{i}}, {{{\tilde{D}}}_{i}}{{{\boldsymbol{\tilde{P}}}}_{i}}$在时间区间[T₀, ∞) 有界，且可通过选择适当的设计参数，使得系统输出y=x₁能够稳定跟踪参考指令信号y_r.

假设在时间区间[T₀, T_r) 内发生完全失效故障的执行器个数为p_r(0≤p_r≤m-1)，用集合M_r表示完全失效执行器的集合，M_r表示剩余执行器的集合.则在时刻T_r有

$ \begin{array}{*{20}{l}} {{V_{nr}} = {V_{n - 1}} + \frac{1}{2}e_n^2 + \frac{1}{2}\mathit{\boldsymbol{\tilde W}}_n^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_n^{ - 1}{{\mathit{\boldsymbol{\tilde W}}}_n} + \frac{1}{{2{\gamma _n}}}\tilde D_n^2 + }\\ {\;\;\;\;\;\;\;\frac{1}{2}\sum\limits_{i \in {M_r}}^m {{b_i}{\rho _i}{C_i}{{\mathit{\boldsymbol{\tilde P}}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_n^{ - 1}\mathit{\boldsymbol{\tilde P}}} .} \end{array} $

(24)

由式 (23) 可知

$ {{\dot V}_{nr}} \le - \sum\limits_{i = 1}^n {{k_i}e_i^2} + \sum\limits_{i = 1}^n {\frac{1}{{{\eta _i}}}} . $

(25)

取${{\lambda }_{1}}=\min \{{{k}_{1}}, {{k}_{2}}, \cdots, {{k}_{n}}\}, {{\lambda }_{2}}=\sum\limits_{i=1}^{n}{\frac{1}{{{\eta }_{i}}}}$.则由不等式 (25) 可以得到:

$ 0 \le {V_{nr}}\left( t \right) \le \frac{{{\lambda _2}}}{{{\lambda _1}}} + \left( {{V_{nr}}\left( 0 \right) - \frac{{{\lambda _2}}}{{{\lambda _1}}}} \right){{\rm{e}}^{ - {\lambda _1}t}},t \ge {T_r}. $

由式 (8) 和式 (24) 可得时刻T_r跟踪误差为

$ \begin{array}{l} e = y - {y_r} = {x_1} - {y_r} = {e_1} \le \sqrt {2{V_{nr}}\left( {{T_r}} \right)} \le \\ \;\;\;\;\;\sqrt {2{\lambda _2}/{\lambda _1} + 2\left( {{V_{nr}}\left( 0 \right) - {\lambda _2}/{\lambda _1}} \right){{\rm{e}}^{ - {\lambda _1}{T_r}}}} . \end{array} $

可知，V_nr(t) 最终有界，且存在上界为λ₂/λ₁.通过增大控制器增益k_i(i=1, 2, …, n) 和参数η_i(i=1, 2, …, n) 的值可以使得上界λ₂/λ₁任意小，从而使得跟踪误差e₁=x₁-y_r任意小.

3 仿真算例

为验证控制器的有效性，考虑如下3阶不确定非线性系统:

$ \left\{ \begin{array}{l} {{\dot x}_1} = {f_1}\left( {{x_1}} \right) + {x_2} + {d_1},\\ {{\dot x}_2} = {f_2}\left( {{x_1},{x_2}} \right) + {x_3} + {d_2}\\ {{\dot x}_3} = {f_3}\left( {{x_1},{x_2},{x_3}} \right) + {b_1}{v_1}\left( {{u_{c1}}} \right) + {b_2}{v_2}\left( {{u_{c2}}} \right) + {d_3},\\ y = {x_1}. \end{array} \right. $

式中: f₁(x₁)=0.1x₁²，f₂(x₁, x₂)=0.2e^-x₂+x₁sin (x₂)，f₃(x₁, x₂, x₃)=x₁x₂x₃，b₁=b₂=1，d₁=0.7x₁²sin t，d₂=0.5(x₁²+x₂²) sin t，d₃=0.2(x₁²+x₂²+x₃²) sin t.滤波时间常数τ₁=τ₂=0.05.参考指令信号y_r=0.5[sin t+sin (0.5t)].初始状态[x₁, x₂, x₃]=[0.5, 0, 0].

滞回非线性模型参数设置为

$ {A_1} = {A_2} = 1,{B_1} = {B_2} = 3.163\;5,{C_1} = {C_2} = 0.345. $

选取如下高斯函数作为RBF神经网络的径向基函数：

$ \begin{array}{l} \mathit{\boldsymbol{\xi }}\left( \mathit{\boldsymbol{Z}} \right) = {\left[ {{\xi _1}\left( \mathit{\boldsymbol{Z}} \right), \cdots ,{\xi _l}\left( \mathit{\boldsymbol{Z}} \right)} \right]^{\rm{T}}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\left[ {{{\rm{e}}^{ - {{\left( {Z - {\mu _1}} \right)}^{\rm{T}}}\left( {Z - {\mu _1}} \right)/\sigma _1^2}}, \cdots ,{{\rm{e}}^{ - {{\left( {Z - {\mu _l}} \right)}^{\rm{T}}}\left( {Z - {\mu _l}} \right)/\sigma _l^2}}} \right]. \end{array} $

式中，μ_i=[μ_i1, …, μ_in]^T, i=1, …, l为高斯函数的中心，σ_i, i=1, …, l为高斯函数的宽度.

神经网络参数设置为：$\boldsymbol{\hat{W}}_{1}^{\text{T}}{{\boldsymbol{\xi }}_{1}}$中，l₁=3，μ₁=[μ₁, …, μ_l1]均匀分布在[-4, ]，宽度σ_i=2, i=1, 2, …, l₁；$\boldsymbol{\hat{W}}_{2}^{\text{T}}{{\boldsymbol{\xi }}_{2}}$中，l₂=9，μ₂=[μ₁, …, μ_l2]均匀分布在[-4, 4]×[-4, 4]，宽度σ_i=2, i=1, 2, …, l₂；$\boldsymbol{\hat{W}}_{3}^{\text{T}}{{\boldsymbol{\xi }}_{3}}$中，l₃=729，μ₃=[μ₁, …, μ_l3]均匀分布在[-4, 4]×[-4, 4]×[-4, 4]×[-4, 4]×[-6, 6]×[-6, 6]，宽度σ_i=2, i=1, 2, …, l₂.

选择控制律设计参数为：Γ₁= Γ₂= Γ₃=diag[0.5]，Γ_P=diag[1.0]，γ₁=γ₂=γ₃=0.5，k₁=k₂=2，k₃=5.假设在t=10 s时，执行器v₁发生卡死故障，且卡死位置为v_k1=4.

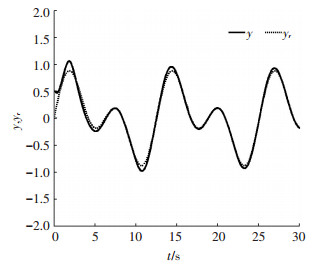
图 2为系统输出跟踪参考指令信号性能曲线，由图 2可知在执行器存在滞回非线性且发生卡死故障情况下系统输出依然能够有效跟踪参考指令信号.

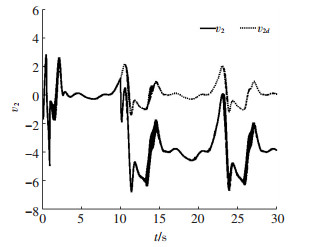
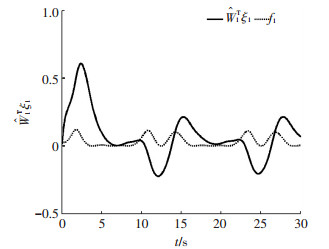
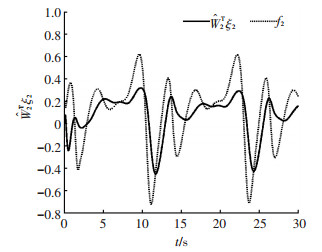
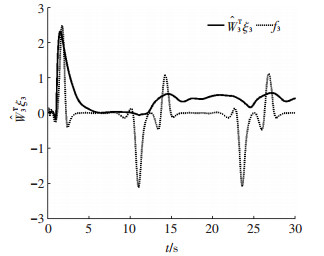
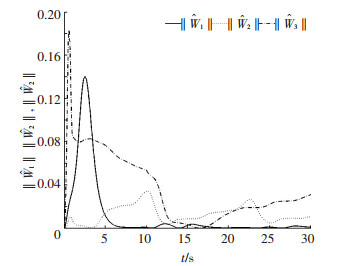
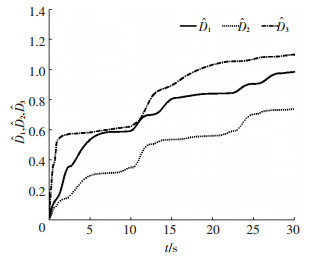
图 3、4分别为两个执行器的输出信号，v_1d, v_2d分别表示执行器未发生故障时的输出值，比较可知在执行器1发生卡死故障情况下，执行器2的输出信号能够保证系统的跟踪性能.图 5~7分别为神经网路逼近系统未知函数项的曲线，可知所设计的自适应RBF神经网络能够实现对不确定系统未知函数项的有效逼近.图 8为神经网络权值范数$\left\| {{{\boldsymbol{\hat{W}}}}_{1}} \right\|, \left\| {{{\boldsymbol{\hat{W}}}}_{2}} \right\|, \left\| {{{\boldsymbol{\hat{W}}}}_{3}} \right\|$的自适应变化曲线，图 9为边界估计值${{{\hat{D}}}_{1}}, {{{\hat{D}}}_{2}}, {{{\hat{D}}}_{3}}$的自适应变化曲线，由图 8、9可知系统中自适应值有界.

4 结论

1) 建立了含有滞回非线性的执行器未知故障模型，并将滞回非线性部分作为系统未知干扰项的一部分，便于控制律的设计.

2) 借鉴动态面控制思想，在Backstepping控制推导过程中引入一阶滤波器，避免对虚拟控制项的直接求导，简化了计算.

3) 通过RBF神经网络和自适应补偿项可以有效消除系统建模过程中非线性函数不确定和外界未知干扰的影响.

4) 设计的鲁棒自适应控制器可以有效保证具有滞回非线性执行器发生故障时闭环系统信号有界，实现对参考指令信号的跟踪.理论分析和仿真结果证明了该方案的有效性.