针对由星敏感器和陀螺组成的姿态估计系统,四元数因计算量小、非奇异性及可全姿态工作等优点常被作为其姿态描述参数[1].因此,基于四元数非线性姿态估计滤波技术成为研究热点[2-4].由于四元数存在归一化约束限制,许多处理四元数约束的非线性姿态估计算法被提出,主要分为以下几种:1) 四元数强制性约束方法,如范数限制卡尔曼滤波算法[5]、平方根四元数CKF[6]等;2) 将误差四元数作为状态变量,对模型进行降阶处理,转化为无约束的姿态估计模型,如乘性扩展卡尔曼滤波算法[7];3) 将四元数看成是一个旋转矢量,与滤波算法相结合,如四元数状态切换无迹卡尔曼滤波器[8]等;4) 将四元数参数与其他无冗余的三维姿态参数进行切换,如无迹四元数估计法[9]等.其中,两步投影理论[6, 10]是一种有效的方法,将状态估计值分两步投影到约束表面,从而解决四元数规范化问题.
上述研究四元数非线性姿态估计,都是基于准确的量测模型.而在实际应用中,由于光学成像、星图识别等复杂的处理步骤以及网络传输的不可靠性,导致姿态信息输出突然失效,从而引起星敏感器量测丢失现象的发生[11-12],这在状态空间模型上体现为量测模型不确定.此种情况下,基于四元数姿态估计滤波方法研究相对较少.文献[13]针对量测模型不确定的情况采用协方差分配的方法来求取状态估计值.而文献[14]在此基础上,采用校正扩展和无迹卡尔曼滤波相结合的方法,虽然能有效解决量测丢失问题,但无迹卡尔曼滤波算法在高维情况下存在算法稳定性差,滤波精度低的现象,同时未考虑四元数约束.而CKF算法采用三阶球面-相径容积规则[15]产生一组容积点来近似非线性函数的后验分布,相比较于无迹卡尔曼滤波算法,CKF算法具有严格的数学理论支撑,针对高维系统,不存在采样非局部效应,滤波算法的数值稳定性更好,滤波估计精度更高.
基于此,本文在推导基于不确定量测的误差四元数非线性姿态估计模型基础上,提出一种基于不确定量测的四元数约束容积卡尔曼滤波姿态估计算法 (quaternion constrained cubature kalman filter based on uncertain measurements, UCCKF),并通过仿真验证了该算法在量测不确定情况下的有效性.
1 不确定量测的非线性姿态估计模型 1.1 陀螺测量模型一个连续形式的陀螺测量模型可表示为
| $ \left\{ \begin{array}{l} \tilde \omega \left( t \right) = \omega \left( t \right) + \beta \left( t \right) + {\eta _v}\left( t \right),\\ \dot \beta \left( t \right) = {\eta _u}\left( t \right). \end{array} \right. $ |
式中:
| $ \begin{array}{l} \mathit{\boldsymbol{E}}\left\{ {{\eta _v}\left( t \right)\eta _v^{\rm{T}}\left( \tau \right)} \right\} = {\mathit{\boldsymbol{I}}_{3 \times 3}}\sigma _v^2\delta \left( {t - \tau } \right),\\ \mathit{\boldsymbol{E}}\left\{ {{\eta _u}\left( t \right)\eta _u^{\rm{T}}\left( \tau \right)} \right\} = {\mathit{\boldsymbol{I}}_{3 \times 3}}\sigma _u^2\delta \left( {t - \tau } \right). \end{array} $ |
根据文献[1],基于四元数的飞行器轨道动力学方程能够被描述为
| $ \mathit{\boldsymbol{\dot q = }}\frac{1}{2}\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{\omega }}\\ 0 \end{array}} \right] \otimes \mathit{\boldsymbol{q = }}\frac{1}{2}\mathit{\Omega }\left( \mathit{\boldsymbol{\omega }} \right) \cdot \mathit{\boldsymbol{q}}\mathit{\boldsymbol{.}} $ | (1) |
式中:q =[q1 q2 q3 q4]= [ρT q4]为姿态四元数,其中ρ为姿态四元数的矢量部分;ω =[ω1 ω2 ω3]T为陀螺三轴角速率输出矢量;[ω×]表示矢量ω的反对称矩阵.
| $ \begin{array}{l} \mathit{\Omega }\left( \mathit{\boldsymbol{\omega }} \right) = \left[ {\begin{array}{*{20}{c}} { - \left[ {\mathit{\boldsymbol{\omega }} \times } \right]} & \mathit{\boldsymbol{\omega }}\\ { - {\mathit{\boldsymbol{\omega }}^{\rm{T}}}} & 0 \end{array}} \right],\\ \left[ {\mathit{\boldsymbol{\omega }} \times } \right] = \left[ {\begin{array}{*{20}{c}} 0 & { - \omega } & {{\omega _2}}\\ {{\omega _3}} & 0 & { - {\omega _1}}\\ { - {\omega _2}} & {{\omega _1}} & 0 \end{array}} \right], \end{array} $ |
由上述四元数描述的姿态矩阵为
| $ \mathit{\boldsymbol{A}}\left( \mathit{\boldsymbol{q}} \right) = \left( {q_4^2 - {\mathit{\boldsymbol{\rho }}^{\rm{T}}}\mathit{\boldsymbol{\rho }}} \right){\mathit{\boldsymbol{I}}_{3 \times 3}} + 2\mathit{\boldsymbol{\rho }}{\mathit{\boldsymbol{\rho }}^{\rm{T}}} - 2{q_4}\left[ {\mathit{\boldsymbol{\rho }} \times } \right]. $ |
利用四元数乘法,误差四元数能够被定义为
| $ \delta \mathit{\boldsymbol{q = q}} \otimes {{\mathit{\boldsymbol{\hat q}}}^{ - 1}} = {\left[ {\Delta \mathit{\boldsymbol{q}},\Delta e} \right]^{\rm{T}}}. $ | (2) |
式中:q为真实四元数;
假设陀螺误差角速率为δω=ω-
| $ \delta \mathit{\boldsymbol{\dot q = \dot q}} \otimes {{\mathit{\boldsymbol{\hat q}}}^{ - 1}} + \mathit{\boldsymbol{q}} \otimes {{\mathit{\boldsymbol{\dot{\hat{q}}}}}^{ - 1}}, $ | (3) |
式中
| $ {{\mathit{\boldsymbol{\dot{\hat{q}}}}}^{ - 1}} = \frac{1}{2}{{\mathit{\boldsymbol{\hat q}}}^{ - 1}} \otimes {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat \omega }}}\\ 0 \end{array}} \right]^{ - 1}} = - \frac{1}{2}{{\mathit{\boldsymbol{\hat q}}}^{ - 1}} \otimes \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat \omega }}}\\ 0 \end{array}} \right], $ | (4) |
结合式 (1)、(3)、(4) 以及
| $ \delta \mathit{\boldsymbol{\dot q = }}\frac{1}{2}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat \omega }}}\\ 0 \end{array}} \right] \otimes \delta \mathit{\boldsymbol{q}} - \frac{1}{2}\delta \mathit{\boldsymbol{q}} \otimes \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat \omega }}}\\ 0 \end{array}} \right] + \frac{1}{2}\left[ {\begin{array}{*{20}{c}} {\delta \mathit{\boldsymbol{\omega }}}\\ 0 \end{array}} \right] \otimes \delta \mathit{\boldsymbol{q}}, $ | (5) |
由于
| $ \frac{1}{2}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat \omega }}}\\ 0 \end{array}} \right] \otimes \delta \mathit{\boldsymbol{q}} - \frac{1}{2}\delta \mathit{\boldsymbol{q}} \otimes \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat \omega }}}\\ 0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \left[ {\mathit{\boldsymbol{\hat \omega }} \times } \right]\Delta \mathit{\boldsymbol{q}}}\\ 0 \end{array}} \right]. $ | (6) |
假设Δβ表示陀螺漂移估计误差值,则
| $ \left[ {\begin{array}{*{20}{c}} {\delta \mathit{\boldsymbol{\omega }}}\\ 0 \end{array}} \right] \otimes \delta \mathit{\boldsymbol{q}} = \left[ {\begin{array}{*{20}{c}} {\Delta e \cdot \delta \mathit{\boldsymbol{\omega }} - \left[ {\delta \mathit{\boldsymbol{\omega }} \times } \right]\Delta \mathit{\boldsymbol{q}}}\\ { - \delta {\mathit{\boldsymbol{\omega }}^{\rm{T}}}\Delta \mathit{\boldsymbol{q}}} \end{array}} \right], $ | (7) |
然后利用式 (5)、(6)、(7) 可得
| $ \delta \mathit{\boldsymbol{\dot q}} = \left[ {\begin{array}{*{20}{c}} { - \left[ {\mathit{\boldsymbol{\hat \omega }} \times } \right]\Delta \mathit{\boldsymbol{q}} + \frac{1}{2}\left[ {\left( {\Delta \beta + {\eta _v}} \right) \times } \right]\Delta \mathit{\boldsymbol{q}} - \frac{1}{2}\Delta e\left( {\Delta \beta + {\eta _v}} \right)}\\ { - \delta {{\left( {\Delta \beta + {\eta _v}} \right)}^{\rm{T}}}\Delta \mathit{\boldsymbol{q}}} \end{array}} \right]. $ |
将δq与Δβ组成状态向量x =[δqT ΔβT]T,则基于误差四元数的飞行器非线性状态方程可以描述为
| $ \mathit{\boldsymbol{\dot x = }}\left[ {\begin{array}{*{20}{c}} {\delta \mathit{\boldsymbol{\dot q}}}\\ {\Delta \dot \beta } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \left[ {\mathit{\boldsymbol{\hat \omega }} \times } \right]\Delta \mathit{\boldsymbol{q}} + \frac{1}{2}\left[ {\left( {\Delta \beta + {\eta _v}} \right) \times } \right]\Delta \mathit{\boldsymbol{q}} - \frac{1}{2}\Delta e\left( {\Delta \beta + {\eta _v}} \right)}\\ {0.5{{\left( {\Delta \beta + {\eta _v}} \right)}^{\rm{T}}}\Delta \mathit{\boldsymbol{q}}}\\ {{\eta _u}} \end{array}} \right]. $ | (8) |
将式 (8) 进行离散化得姿态估计系统离散状态方程为
| $ {\mathit{\boldsymbol{x}}_{k + 1}} = {f_k}\left( {{\mathit{\boldsymbol{x}}_k},\mathit{\boldsymbol{\hat \omega }}} \right) + {w_k}. $ | (9) |
式中wk均值为零,方差为Qk的高斯白噪声.
1.3 系统量测方程若星敏感器的输出为光轴在本体坐标系上的参考矢量,则星敏感器测量模型表示为
| $ \begin{array}{l} z_k^i = \mathit{\boldsymbol{A}}\left( {\mathit{\boldsymbol{q}}\left( {{t_k}} \right)} \right){{\mathit{\boldsymbol{\vec r}}}^i} + \mathit{\boldsymbol{v}}_k^i = \mathit{\boldsymbol{A}}\left( {\delta \mathit{\boldsymbol{q}} \otimes \mathit{\boldsymbol{\hat q}}} \right){{\mathit{\boldsymbol{\vec r}}}^i} + \mathit{\boldsymbol{v}}_k^i = \\ \mathit{\boldsymbol{A}}\left( {\delta \mathit{\boldsymbol{q}}} \right)\mathit{\boldsymbol{A}}\left( {\mathit{\boldsymbol{\hat q}}} \right){{\mathit{\boldsymbol{\vec r}}}^i} + \mathit{\boldsymbol{v}}_k^i. \end{array} $ |
式中:i为星敏感器观测到第i颗恒星;zki为第i颗恒星对应的星敏感器输出矢量;
| $ {\mathit{\boldsymbol{z}}_k} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{z}}_k^1}\\ {\mathit{\boldsymbol{z}}_k^2}\\ {\mathit{\boldsymbol{z}}_k^3} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{A}}\left( {\delta \mathit{\boldsymbol{q}}} \right)\mathit{\boldsymbol{A}}\left( {\mathit{\boldsymbol{\hat q}}} \right){{\mathit{\boldsymbol{\vec r}}}^1}}\\ {\mathit{\boldsymbol{A}}\left( {\delta \mathit{\boldsymbol{q}}} \right)\mathit{\boldsymbol{A}}\left( {\mathit{\boldsymbol{\hat q}}} \right){{\mathit{\boldsymbol{\vec r}}}^2}}\\ {\mathit{\boldsymbol{A}}\left( {\delta \mathit{\boldsymbol{q}}} \right)\mathit{\boldsymbol{A}}\left( {\mathit{\boldsymbol{\hat q}}} \right){{\mathit{\boldsymbol{\vec r}}}^3}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{v}}_k^1}\\ {\mathit{\boldsymbol{v}}_k^2}\\ {\mathit{\boldsymbol{v}}_k^3} \end{array}} \right] = h\left( {{\mathit{\boldsymbol{x}}_k}} \right) + {\mathit{\boldsymbol{v}}_k}. $ |
式中: zk为星敏感器的输出矢量;h(xk) 为非线性量测函数;vk为高斯白噪声,其均值为零,方差为Rk.
如果考虑星敏感器的量测存在丢失或是不确定的情况,则带量测不确定的星敏感器测量模型为
| $ {\mathit{\boldsymbol{z}}_k} = {\lambda _k}h\left( {{\mathit{\boldsymbol{x}}_k}} \right) + {\mathit{\boldsymbol{v}}_k}, $ | (10) |
式中:λk表示描述量测中的不确定性,作为独立的伯努利随机变量,取值为0或1,P[λk=1]=pk表示量测没有出现错误的概率,则λk的均值和方差分别为pk和 (1-pk)pk.
2 UCCKF算法 2.1 三阶球面-相径容积规则假设随机变量x的维数为n维,它服从均值为
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\mathit{\boldsymbol{\hat z}} = \int {f\left( \mathit{\boldsymbol{x}} \right)N\left( {\mathit{\boldsymbol{x}};\mathit{\boldsymbol{\hat x}},{\mathit{\boldsymbol{P}}_x}} \right){\rm{d}}x} ,\\ {\mathit{\boldsymbol{P}}_z} = \int {\left( {f\left( \mathit{\boldsymbol{x}} \right) - \mathit{\boldsymbol{\hat z}}} \right){{\left( {f\left( \mathit{\boldsymbol{x}} \right) - \mathit{\boldsymbol{\hat z}}} \right)}^{\rm{T}}}N\left( {\mathit{\boldsymbol{x}};\mathit{\boldsymbol{\hat x}},{\mathit{\boldsymbol{P}}_x}} \right){\rm{d}}x} = \\ \;\;\;\;\;\;\;\int {f\left( \mathit{\boldsymbol{x}} \right){f^{\rm{T}}}\left( \mathit{\boldsymbol{x}} \right)N\left( {\mathit{\boldsymbol{x}};\mathit{\boldsymbol{\hat x}},{\mathit{\boldsymbol{P}}_x}} \right){\rm{d}}x - \mathit{\boldsymbol{\hat z}}{{\mathit{\boldsymbol{\hat z}}}^{\rm{T}}},} \\ {\mathit{\boldsymbol{P}}_{xz}} = \int {\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{\hat x}}} \right){{\left( {f\left( \mathit{\boldsymbol{x}} \right) - \mathit{\boldsymbol{\hat z}}} \right)}^{\rm{T}}}N\left( {\mathit{\boldsymbol{x}};\mathit{\boldsymbol{\hat x}},{\mathit{\boldsymbol{P}}_x}} \right){\rm{d}}x} = \\ \;\;\;\;\;\;\;\;\int {\mathit{\boldsymbol{x}}{\mathit{f}^{\rm{T}}}\left( \mathit{\boldsymbol{x}} \right)N\left( {\mathit{\boldsymbol{x}};\mathit{\boldsymbol{\hat x}},{\mathit{\boldsymbol{P}}_x}} \right){\rm{d}}\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{\hat x}}{{\mathit{\boldsymbol{\hat z}}}^{\rm{T}}}} . \end{array} $ |
上述3个等式可以看出要想获得精确解析解,重点在于多元积分的求解.而根据数学积分理论,对于
非线性函数z的均值
1) 将Px进行Cholesky分解.
| $ {\mathit{\boldsymbol{P}}_x} = \mathit{\boldsymbol{S}}{\mathit{\boldsymbol{S}}^{\rm{T}}}. $ |
2) 容积点的求取.
| $ {\mathit{\boldsymbol{\alpha }}_i} = \mathit{\boldsymbol{S}}{\xi _i} + \mathit{\boldsymbol{\hat x}},{\xi _i} = \sqrt {\frac{m}{2}} {\left[ 1 \right]_i},{\omega _i} = \frac{1}{m}\left( {i = 1, \cdots ,m} \right). $ | (11) |
式中:m=2n;假设n维的单位向量用e =[1, 0, …, 0]T来表示,任意改变e中元素的符号或是对其元素进行全排列得到的所有单位向量的集合表示为点集[1],则[1]i就为点集[1]中的第i个点;ξi为第i个容积点;ωi为相应容积点的权值.
3) 容积点经过非线性函数的传递值为
| $ {\gamma _i} = f\left( {{\alpha _i}} \right). $ |
4) z的均值
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat z}} = \frac{1}{m}\sum\limits_{i = 1}^m {{\gamma _i}} ,}\\ {{\mathit{\boldsymbol{P}}_z} = \frac{1}{m}\sum\limits_{i = 1}^m {{\gamma _i}\gamma _i^{\rm{T}}} - \hat z{{\hat z}^{\rm{T}}},}\\ {{\mathit{\boldsymbol{P}}_{xz}} = \frac{1}{m}\sum\limits_{i = 1}^m {{\alpha _i}\gamma _i^{\rm{T}}} - \hat x{{\hat z}^{\rm{T}}}.} \end{array} $ |
针对式 (10) 的不确定量测,由于λk、xk以及vk是相互独立的,则zk的均值、方差以及互协方差分别为:
| $ \mathit{\boldsymbol{E}}\left[ {{\mathit{\boldsymbol{z}}_k}} \right] = \mathit{\boldsymbol{E}}\left[ {{\lambda _k}h\left( {{\mathit{\boldsymbol{x}}_k}} \right) + {\mathit{\boldsymbol{v}}_k}} \right] = {p_k}\mathit{\boldsymbol{E}}\left[ {h\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right], $ | (12) |
| $ \begin{array}{l} \mathit{\boldsymbol{Cov}}\left( {{\mathit{\boldsymbol{z}}_k}} \right) = \mathit{\boldsymbol{E}}\left[ {\left( {{\mathit{\boldsymbol{z}}_k} - \mathit{\boldsymbol{E}}\left[ {{\mathit{\boldsymbol{z}}_k}} \right]} \right){{\left( {{\mathit{\boldsymbol{z}}_k} - \mathit{\boldsymbol{E}}\left[ {{\mathit{\boldsymbol{z}}_k}} \right]} \right)}^{\rm{T}}}} \right] = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{E}}\left[ {{\mathit{\boldsymbol{z}}_k}\mathit{\boldsymbol{z}}_k^{\rm{T}}} \right] - \mathit{\boldsymbol{E}}\left[ {{\mathit{\boldsymbol{z}}_k}} \right]{\left( {\mathit{\boldsymbol{E}}\left[ {{\mathit{\boldsymbol{z}}_k}} \right]} \right)^{\rm{T}}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{E}}\left[ {{\lambda _k}h\left( {{\mathit{\boldsymbol{x}}_k}} \right)h{{\left( {{\mathit{\boldsymbol{x}}_k}} \right)}^{\rm{T}}}\lambda _k^{\rm{T}}} \right] - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;p_k^2\mathit{\boldsymbol{E}}\left[ {h\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right]{\left( {\mathit{\boldsymbol{E}}\left[ {h\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right]} \right)^{\rm{T}}} + {\mathit{\boldsymbol{R}}_k} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{E}}\left[ {{\lambda _k}\lambda _k^{\rm{T}}} \right]\mathit{\boldsymbol{E}}\left[ {h\left( {{\mathit{\boldsymbol{x}}_k}} \right)h{{\left( {{\mathit{\boldsymbol{x}}_k}} \right)}^{\rm{T}}}} \right] - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;p_k^2\mathit{\boldsymbol{E}}\left[ {h\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right]{\left( {\mathit{\boldsymbol{E}}\left[ {h\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right]} \right)^{\rm{T}}} + {\mathit{\boldsymbol{R}}_k} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{p_k}\left[ {\mathit{\boldsymbol{Cov}}\left( {h\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right) + \mathit{\boldsymbol{E}}\left[ {h\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right]} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{{\left( {\mathit{\boldsymbol{E}}\left[ {h\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right]} \right)}^{\rm{T}}}} \right] - p_k^2\mathit{\boldsymbol{E}}\left[ {h\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right] \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {\mathit{\boldsymbol{E}}\left[ {h\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right]} \right)^{\rm{T}}} + {\mathit{\boldsymbol{R}}_k} = {p_k}\mathit{\boldsymbol{Cov}}\left( {h\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{p_k}\left( {1 - {p_k}} \right)\mathit{\boldsymbol{E}}\left[ {h\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right]{\left( {\mathit{\boldsymbol{E}}\left[ {h\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right]} \right)^{\rm{T}}} + {\mathit{\boldsymbol{R}}_k}, \end{array} $ | (13) |
| $ \begin{array}{l} \mathit{\boldsymbol{Cov}}\left( {{\mathit{\boldsymbol{x}}_k},{\mathit{\boldsymbol{z}}_k}} \right) = \mathit{\boldsymbol{Cov}}\left( {{\mathit{\boldsymbol{x}}_k},{\lambda _k}h\left( {{\mathit{\boldsymbol{x}}_k}} \right) + {\mathit{\boldsymbol{v}}_k}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{Cov}}\left( {{\mathit{\boldsymbol{x}}_k},{\lambda _k}h\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{p_k}\mathit{\boldsymbol{Cov}}\left( {{\mathit{\boldsymbol{x}}_k},h\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right). \end{array} $ | (14) |
为了获得上述zk的统计特性,需要知道E[h(xk)],Cov(h(xk)) 以及Cov(xk, h(xk)) 的值,本文采用上述三阶球面-相径容积规则来近似获得,假设xk的统计特性为N(xk;
| $ \mathit{\boldsymbol{E}}\left[ {h\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right] \approx \sum\limits_{i = 1}^{2n} {{\mathit{\boldsymbol{\omega }}_i}h\left( {{\mathit{\boldsymbol{\chi }}_i}} \right)} , $ | (15) |
| $ \begin{array}{l} \mathit{\boldsymbol{Cov}}\left( {h\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right) = \sum\limits_{i = 1}^{2n} {{\mathit{\boldsymbol{\omega }}_i}h\left( {{\mathit{\boldsymbol{\chi }}_i}} \right)h{{\left( {{\mathit{\boldsymbol{\chi }}_i}} \right)}^{\rm{T}}}} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\mathit{\boldsymbol{E}}\left[ {h\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right]} \right)\mathit{\boldsymbol{E}}{\left[ {h\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right]^{\rm{T}}}, \end{array} $ | (16) |
| $ \mathit{\boldsymbol{Cov}}\left( {{\mathit{\boldsymbol{x}}_k},h\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right) = \sum\limits_{i = 1}^{2n} {{\mathit{\boldsymbol{\omega }}_i}{\mathit{\boldsymbol{\chi }}_i}h{{\left( {{\mathit{\boldsymbol{\chi }}_i}} \right)}^{\rm{T}}} - {{\mathit{\hat x}}_k}\mathit{\boldsymbol{E}}{{\left[ {h\left( {{\mathit{\boldsymbol{x}}_k}} \right)} \right]}^{\rm{T}}}} . $ | (17) |
式中χi为容积点,ωi为相应的权值,可以根据式 (11) 求出.
2.3 UCCKF算法针对由式 (9) 和式 (10) 组成的非线性姿态估计系统,同时考虑量测不确定和四元数约束两种情况,并利用三阶球面-相径容积规则近似非线性函数的后验均值和协方差,给出了一种UCCKF算法.其算法流程如下.
2.3.1 时间更新已知k-1时刻状态xk-1的均值和方差分别为
| $ {\mathit{\boldsymbol{\alpha }}_{i,k - 1}} = {\mathit{\boldsymbol{S}}_{k - 1}}{\mathit{\boldsymbol{\xi }}_i} + {{\mathit{\boldsymbol{\hat x}}}_{k - 1|k - 1}}, $ |
式中Pk-1= Sk-1 Sk-1T.
将上述容积点经状态非线性函数的传递值为
| $ {\gamma _{i,k|k - 1}} = f\left( {{\mathit{\alpha }_{i,k - 1}}} \right). $ |
一步状态预测
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat x}}}_{k|k - 1}} = \frac{1}{m}\sum\limits_{i = 1}^m {{\gamma _{i,k|k - 1}}} ,}\\ {{\mathit{\boldsymbol{P}}_{k|k - 1}} = \frac{1}{m}\sum\limits_{i = 1}^m {{\gamma _{i,k|k - 1}}\gamma _{i,k|k - 1}^{\rm{T}}} - {{\hat x}_{i,k|k - 1}}\hat x_{i,k|k - 1}^{\rm{T}} + {\mathit{\boldsymbol{Q}}_{k - 1}}.} \end{array} $ |
利用一步状态预测
| $ {\mathit{\boldsymbol{\alpha }}_{i,k|k - 1}} = {\mathit{\boldsymbol{S}}_{k|k - 1}}{\mathit{\boldsymbol{\xi }}_i} + {{\mathit{\boldsymbol{\hat x}}}_{k - 1|k - 1}}, $ |
式中Pk|k-1= Sk|k-1Sk|k-1T.
将上述容积点经量测非线性函数的传递值为
| $ {\mathit{\boldsymbol{\gamma }}_{i,k}} = h\left( {{\mathit{\boldsymbol{\alpha }}_{i,k|k - 1}}} \right). $ |
由式 (15)~(17) 可以求出关于y=h(xk)的统计特性,其均值、方差以及互协方差为:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot y}}}_{k|k - 1}} \approx \sum\limits_{i = 1}^{2n} {{\omega _i}{\gamma _{i,k}},} }\\ {{\mathit{\boldsymbol{P}}_{yy}} = \sum\limits_{i = 1}^{2n} {{\omega _i}{\gamma _{i,k}}\gamma _{i,k}^{\rm{T}}} - {y_{k|k - 1}}y_{k|k - 1}^{\rm{T}},}\\ {{\mathit{\boldsymbol{P}}_{xy}} = \sum\limits_{i = 0}^{2n} {{\omega _i}{\mathit{\boldsymbol{\alpha }}_{i,k|k - 1}}\gamma _{i,k}^{\rm{T}}} - {{\hat x}_{k|k - 1}}y_{k|k - 1}^{\rm{T}}.} \end{array} $ |
再根据式 (12)~(14) 可以求出不确定量测下zk的均值、方差以及互协方差为:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat z}}}_{k|k - 1}} = {p_k}{{\mathit{\boldsymbol{\hat y}}}_{k|k - 1}},}\\ {{\mathit{\boldsymbol{P}}_{zz}} = {p_k}{\mathit{\boldsymbol{P}}_{yy}} + {p_k}\left( {1 - {p_k}} \right){{\mathit{\boldsymbol{\hat y}}}_{k|k - 1}}\mathit{\boldsymbol{\hat y}}_{k|k - 1}^{\rm{T}} + {\mathit{\boldsymbol{R}}_k},}\\ {{\mathit{\boldsymbol{P}}_{xz}} = {p_k}{\mathit{\boldsymbol{P}}_{xy}},} \end{array} $ |
则无四元数约束下的状态估计及协方差为:
| $ {{\mathit{\boldsymbol{\bar x}}}_{k|k}} = {{\mathit{\boldsymbol{\hat x}}}_{k|k - 1}} + {\mathit{\boldsymbol{P}}_{xz}}\mathit{\boldsymbol{P}}_{zz}^{ - 1}\left( {{\mathit{\boldsymbol{z}}_k} - {{\mathit{\boldsymbol{\hat z}}}_{k|k - 1}}} \right), $ | (18) |
| $ {{\mathit{\boldsymbol{\bar P}}}_k} = {\mathit{\boldsymbol{P}}_{k|k - 1}} - {\mathit{\boldsymbol{P}}_{xz}}\mathit{\boldsymbol{P}}_{zz}^{ - 1}\mathit{\boldsymbol{P}}_{xz}^{\rm{T}}. $ | (19) |
由于四元数存在归一化的限制,即姿态估计系统的部分状态量存在四元数约束情况,如果不考虑状态约束直接作滤波处理,滤波精度差,甚至会导致协方差奇异.因此需要对滤波方法进行改进,而文献[2]的强制性约束只是简单的将姿态估计值投影到四元数约束表面,对姿态估计方差没有调整,这会引起滤波精度的下降,由于四元数约束本质上是属于非线性等式约束,因此,本文采用文献[10]提出的两步投影理论来解决非线性四元数约束问题.第1步投影将无约束的状态估计分布投影到约束表面,使得姿态估计分布满足四元数约束,但是这会引起姿态估计方差的下降.第2步投影则将约束的状态估计分布投影到约束表面,使得姿态估计均值满足四元数约束,同时对姿态估计方差进行补偿,从而在保证四元数规范化的同时提高姿态估计的精度.
由于状态变量xk中,误差四元数δq满足约束c(xk)=δqTδq-1,则将无约束状态投影到约束表面为
| $ {{\mathit{\boldsymbol{\tilde x}}}_k} = g\left( {{\mathit{\boldsymbol{x}}_k}} \right). $ |
式中:
利用两步投影理论对式 (18)、(19) 中未约束的状态估计进行处理.
第1步投影 为使无约束状态估计分布满足非线性等式约束,将其投影到约束表面,从而得到约束的状态估计分布均值和方差分别为:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\chi }}_k}\left( i \right) = {{\mathit{\boldsymbol{\bar x}}}_{k|k}} + {{\mathit{\boldsymbol{\bar S}}}_k}{\mathit{\boldsymbol{\xi }}_i},}\\ {{{\mathit{\boldsymbol{\bar \chi }}}_k}\left( i \right) = g\left( {{\mathit{\boldsymbol{\chi }}_k}\left( i \right)} \right),}\\ {{{\mathit{\boldsymbol{\vec x}}}_{k|k}} = \sum\limits_{i = 1}^{2n} {{\omega _i}{{\mathit{\boldsymbol{\tilde \chi }}}_k}\left( i \right)} ,}\\ {{{\mathit{\boldsymbol{\vec P}}}_k} = \sum\limits_{i = 1}^{2n} {{\omega _i}\left( {{{\mathit{\boldsymbol{\tilde \chi }}}_k}\left( i \right) - {{\mathit{\boldsymbol{\vec x}}}_k}} \right){{\left( {{{\mathit{\boldsymbol{\tilde \chi }}}_k}\left( i \right) - {{\mathit{\boldsymbol{\vec x}}}_k}} \right)}^{\rm{T}}}} ,} \end{array} $ |
式中Pk= Sk SkT.
第2步投影 为使第1步得到的约束状态估计分布均值满足约束条件,将其投影到约束表面,同时对估计方差进行补偿,从而得到最后的状态估计
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat x}}}_{k|k}} = g\left( {{{\mathit{\boldsymbol{\vec x}}}_{k|k}}} \right),}\\ {{{\mathit{\boldsymbol{\hat P}}}_k} = {{\mathit{\boldsymbol{\vec P}}}_k} + \left( {{{\mathit{\boldsymbol{\hat x}}}_{k|k}} - {{\mathit{\boldsymbol{\vec x}}}_{k|k}}} \right){{\left( {{{\mathit{\boldsymbol{\hat x}}}_{k|k}} - {{\mathit{\boldsymbol{\vec x}}}_{k|k}}} \right)}^{\rm{T}}}.} \end{array} $ |
从上述推导可以看出,当p=1,即不存在量测不确定情况,则UCCKF退化为约束容积卡尔曼滤波 (constrained cubature Kalman filter, CCKF).
3 仿真实验及分析首先将陀螺与星敏感器组合成非线性姿态估计系统,建立相关的仿真实验平台.利用陀螺和星敏感器两个姿态传感器进行数据测量.陀螺实物传感器被用于输出角速率信息,其陀螺测量噪声为σv=0.05 (°)/h,陀螺漂移噪声设σu=0.003 (°)/h,采样频率为100 Hz;一个星敏感器仿真器被用于产生带测量噪声的矢量数据,该星敏感器能够在视场6°×6°的范围内最多观测到10颗星,其采样频率被设置为1 Hz,星敏感器测量噪声设为σs=18″;初始陀螺常值漂移被设置为β=[1 1 1]T(°)/h;假设初始时刻无初始姿态误差以及陀螺漂移估计误差;初始姿态与陀螺漂移的估计值均设为零;初始方差阵分别设为 (0.2°)2 I3×3和 (1.2(°)/h)2 I3×3.
基于上述仿真实验平台,为更好验证本文提出的UCCKF算法的有效性,将其与CCKF算法以及文献[14]中的无迹混合滤波算法 (unscented mixture filter, UMF) 进行比较和分析.同时,UMF算法用于非线性姿态估计系统,需考虑四元数约束,因此,在其每步状态更新后加上强制性的四元数约束.仿真时间设为800 s.仿真结果如图 1~3所示.

|
图 1 当p=0.1时姿态误差 Figure 1 Attitude estimation errors when p=0.1 |

|
图 2 当p=0.5时姿态误差 Figure 2 Attitude estimation errors when p=0.5 |
|
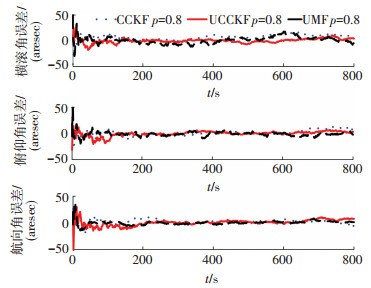
图 3 当p=0.8时姿态误差 Figure 3 Attitude estimation errors when p=0.8 |
图 1、2显示的是当星敏感器未出现量测丢失的概率分别为p=0.1和p=0.5时滤波得到的姿态误差对比图.从这两个图中可以明显看出,CCKF滤波算法随着仿真时间的增加姿态误差不断增大,而UMF算法和本文提出的UCCKF算法则未出现明显的滤波发散现象,算法较为稳定,算法收敛精度都能达到20 arcsec.同时随着星敏感器未出现量测丢失的概率p不断增大,这3种算法的滤波精度均有所提高.这些现象出现的原因是CCKF滤波算法设计未考虑量测丢失的影响从而导致在出现量测丢失的情况下滤波算法不稳定,估计精度降低.而UMF算法和UCCKF算法均在算法设计中考虑了量测丢失的影响,当星敏感器量测丢失出现时,算法均能收敛,保持稳定.图 3显示的是当星敏感器未出现量测丢失的概率p=0.8时姿态误差的对比图,从图 3中可以看出,3种算法均能收敛,估计精度相当.这是由于星敏感器出现正确量测的概率较高,因此对CCKF算法的影响减小,CCKF算法能够收敛,且估计精度影响不大.
为了体现算法比较的公正性以及更好地比较算法稳态时的估计性能,姿态角的均方根误差 (root-mean square error, RMSE) 被采用来描述姿态估计的质量,它被定义为
| $ {\rm{RMS}}{{\rm{E}}_{{\rm{att}}}}\left( k \right) = \sqrt {\frac{1}{{{N_{{\rm{MC}}}}}}\sum\limits_{i = 1}^{{N_{{\rm{MC}}}}} {{{\left\| {\mathit{\boldsymbol{a}}{\mathit{\boldsymbol{e}}_i}\left( k \right)} \right\|}^2}} } . $ |
式中: aei(k) 为第i次蒙特卡罗仿真姿态误差向量;NMC为蒙特卡罗仿真的总次数,仿真中将其设为NMC=50.
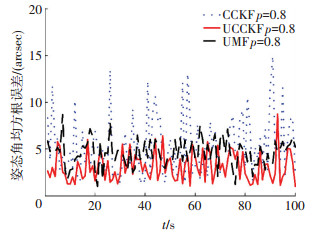
图 4显示的是当星敏感器出现正确量测的概率p=0.8时3种算法的姿态角均方误差对比图.从图 4中可以看出,此种情况下UCCKF算法的稳态精度要高于CCKF算法和UMF算法.这是因为,相比较于CCKF算法,UCCKF算法能够处理星敏感器量测丢失,滤波估计精度要高于CCKF算法.UMF算法虽然也能补偿星敏感器量测丢失导致的模型误差,但是它是以UKF算法为基础,且采用强制性的四元数约束方法,对算法的精度有一定的影响,而UCCKF算法是以CKF算法为基础,利用两步投影理论确保满足四元数约束条件,因此,在高维以及量测不确定的情况下,UCCKF的滤波性能更好.
|
图 4 当p=0.8时姿态角均方误差 Figure 4 RMSE in attitude when p=0.8 |
1) 针对星敏感器量测丢失导致的量测模型不确定问题,建立了基于不确定量测的误差四元数非线性姿态估计模型,所建立的模型对姿态估计算法的研究提供支撑.
2) 提出了一种基于不确定量测的四元数约束容积卡尔曼滤波算法,解决了上述模型中存在的四元数约束和量测不确定问题.仿真结果表明,该算法在量测不确定情况下具有更好的收敛性和更高的估计精度,验证了算法的合理性和有效性.
| [1] | CHANG Lubin, HU Baiqing, CHANG Guobin. Modified unscented quaternion estimator based on quaternion averaging[J]. Journal of Guidance, Control and Dynamics, 2013, 37(1): 305-309. DOI: 10.2514/1.61723 |
| [2] |
钱华明, 黄蔚, 孙龙. 基于改进的迭代容积卡尔曼滤波姿态估计[J].
哈尔滨工业大学学报, 2014, 46(6): 116-122.
QIAN Huaming, HUANG Wei, SUN Long. Attitude estimation based on improved iterated cubature Kalman filter[J]. Journal of Harbin Institute of Technology, 2014, 46(6): 116-122. DOI: 10.11918/j.issn.0367-6234.2014.06.021 |
| [3] |
王硕, 宋申民, 史小平, 等. 噪声特性未知的多传感器协方差交叉融合姿态估计[J].
控制与决策, 2016, 31(2): 273-278.
WANG Shuo, SONG Shenmin, SHI Xiaoping, et al. Multi-sensor covariance intersection fusion attitude estimation with unknown noise characteristics[J]. Control and Decision, 2016, 31(2): 273-278. DOI: 10.13195/j.kzyjc.2014.1417 |
| [4] | QIAN Huaming, HUANG Wei, QIAN Linchen, at al. Robust extended Kalman filter for attitude estimation with multiplicative noises and unknown external disturbances[J]. IET Control Theory & Applications, 2014, 8(15): 1523-1536. DOI: 10.1049/iet-cta.2014.0293 |
| [5] | ZANETTI R, MAJJI M, BISHOP R H, at al. Norm-constrained Kalman filtering[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(5): 1458-1465. DOI: 10.2514/1.43119 |
| [6] | TANG Xiaojun, LIU Zhenbao, ZHANG Jiasheng. Square-root quaternion cubature Kalman filtering for spacecraft attitude estimation[J]. Acta Astronautica, 2012, 76: 84-94. DOI: 10.1016/j.actaastro.2012.02.009 |
| [7] | LEFFERTS E J, MARKLEY F L, SHUSTER M D. Kalman filtering for spacecraft attitude estimation[J]. Journal of Guidance, Control, and Dynamics, 1982, 5(5): 417-429. DOI: 10.2514/3.56190 |
| [8] |
乔相伟, 周卫东, 吉宇人. 用四元数状态切换无迹卡尔曼滤波器估计的飞行器姿态[J].
控制理论与应用, 2012, 29(1): 97-103.
QIAO Xiangwei, ZHOU Weidong, JI Yuren. Aircraft attitude estimation based on quaternion state-switching unscented Kalman filter[J]. Control Theory & Applications, 2012, 29(1): 97-103. DOI: 10.7641/j.issn.1000-8152.2012.1.CCTA100514 |
| [9] | CRASSIDIS J L, MARKLEY F L. Unscented filtering for spacecraft attitude estimation[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(4): 536-542. DOI: 10.2514/2.5102 |
| [10] | JULIER S J, LAVIOLA J J. On Kalman filtering with nonlinear equality constraints[J]. IEEE Transactions on Signal Processing, 2007, 55(6): 2774-2784. DOI: 10.1109/TSP.2007.893949 |
| [11] | WANG Shuang, GENG Yunhai, JIN Rongyu. A novel error model of optical systems and an on-orbit calibration method for star sensors[J]. Sensors, 2015, 15(12): 31428-31441. DOI: 10.3390/s151229863 |
| [12] | HUANG Wei, XIE Hongsheng, SHEN Chen, et al. A robust strong tracking cubature Kalman filter for spacecraft attitude estimation with quaternion constraint[J]. Acta Astronautica, 2016, 121: 153-163. DOI: 10.1016/j.actaastro.2016.01.009 |
| [13] | NANACARA W, YAZ E E. Recursive estimator for linear and nonlinear systems with uncertain observations[J]. Signal Processing, 1997, 62(1): 215-228. DOI: 10.1016/S0165-1684(97)00126-6 |
| [14] | HERMOSO-CARAZO A, LINNARES-PEREZ J. Different approaches for state filtering in nonlinear systems with uncertain observations[J]. Applied Mathematics and Computation, 2007, 187(2): 708-724. DOI: 10.1016/j.amc.2006.08.083 |
| [15] | ARASARATNAM I, HAYKIN S. Cubature Kalman filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254-1269. DOI: 10.1109/TAC.2009.2019800 |
 2017, Vol. 49
2017, Vol. 49


