2. 中国民航大学 航空工程学院, 天津 300300;
3. 天津市高速切削与精密加工重点实验室 (天津职业技术师范大学),天津 300222
2. School of Aeronautical Engineering, Civil Aviation University of China, Tianjin 300300, China;
3. Tianjin Key Laboratory of High Speed Cutting and Precision Machining (Tianjin University of Technology and Education), Tianjin 300222, China
求解瑞雷波频散的本征值问题是瑞雷波理论和应用研究的重要基础,1953年,Haskell[1]改进了Thompson[2]的算法,提出传递矩阵算法,可以快速、有效地求解弹性层状介质中瑞雷波本征值.此后,Knopoff[3]和Abo-Zena[4]分别以此为基础提出改进算法,提高计算速度和高频数值稳定性.凡友华等[5]在此基础上提出了快速标量传递算法,提高了计算速度.1993年,Chen[6]在Kennett[7]的反射/透射系数法基础上提出了广义反射/透射系数法,从根本上解决了以往算法中高频数值不稳定的问题.在这之后也有学者[8-9]将该算法修正,分别提高了稳定性和速度.
以往关于瑞雷波研究更多的是基于弹性假设.但实际上很多介质都表现出一定的黏弹性,因此有必要研究黏弹性层状介质中瑞雷波的理论及应用,其中重要的基础就是本征值问题求解.过去往往用Muller法[10]或牛顿法[11]进行求解.例如,Cao等[12]在2010年提出了一种将Muller法与牛顿法结合使用的Love波本征值问题求解方法,但是每个频率下本征值计算要依赖于前一个频率的本征值.而张凯[13]在2011年采用Muller法进行了求解.除此之外,Lai等[14]于2004年基于复分析中的柯西留数定理提出了一种求解方法.然而,这些方法都普遍存在着漏根及多根的问题,尤其在高频下更为严重.本文将研究黏弹性层状介质中瑞雷波本征值求解中的漏根和多根问题,并基于Muller法给出一种求解方法以避免漏根和多根问题.
1 本征值求解的基本方法瑞雷波频散的本征值问题需要求解一系列的本征值,且要避免漏根问题,因此采用简单的有限元方法或者求解奇异值方法并不适用.目前已有很多种不同形式的弹性层状介质中瑞雷波本征函数,其本质上是等价的,只是在求解对应的本征值问题时在数值稳定性及速度上有差异.Christensen[15]证明,对于黏弹性情况,瑞雷波的本征函数的形式是相同的,只是函数中原本取值为实数的弹性模量变为取复值的黏弹性介质复模量.因此,黏弹性层状介质中瑞雷波的频散方程是一个高度非线性的复函数方程,这一类方程的求解比弹性情况下的实方程更复杂.黏弹性层状介质中瑞雷波的本征函数是一个高度非线性的复函数,因此它的求解比弹性情况更加复杂.而且由于瑞雷波发生频散后的同频率下往往有若干个衰减系数和相速度,且彼此间差别有时较小,因此采用简单的将本征值复根的实部和虚部分别细分并进行逼近不仅计算量无法接受,而且很容易发生漏根现象.Muller法可以用于这类方程的求解,下面简单叙述利用Muller法求解该方程的过程.
设黏弹性层状介质中瑞雷波的频散方程为F(c)=0,其中F(c) 即为本征函数,c为本征值,即瑞雷波的复速度.Muller法对方程求解需要给出3个初值 (c0, F(c0)), (c1, F(c1)), (c2, F(c2)),然后利用以下迭代公式计算下一个值c3为
| $ {{c}_{3}}={{c}_{2}}-\frac{2C}{B+\text{sign}(B)\sqrt{{{B}^{2}}+4AC}}, $ | (1) |
其中:
| $ \begin{array}{*{20}{c}} {A = \frac{{F\left( {{c_0}} \right) - F\left( {{c_2}} \right)}}{{\left( {{c_0} - {c_2}} \right)\left( {{c_0} - {c_1}} \right)}} - \frac{{F\left( {{c_1}} \right) - F\left( {{c_2}} \right)}}{{\left( {{c_1} - {c_2}} \right)\left( {{c_0} - {c_1}} \right)}},}\\ {B = \frac{{{{\left( {{c_0} - {c_2}} \right)}^2} - {{\left( {{c_1} - {c_2}} \right)}^2}}}{{\left( {{c_0} - {c_2}} \right)\left( {{c_1} - {c_2}} \right)\left( {{c_0} - {c_1}} \right)}}\left( {F\left( {{c_1}} \right) - F\left( {{c_2}} \right)} \right),}\\ {C = F\left( {{c_2}} \right).} \end{array} $ |
在得到c3后,令c0= c1, c1= c2, c2= c3,由此可以再计算下一个迭代值c3.直到函数值F(c3) 的绝对值满足所求精度或达到最大迭代次数.
总的来说,对于一个给定的频率,为求解频散方程,大体计算步骤如下:
1) 确定瑞雷波的相速度存在范围[VRmin, VSmax],即大于各层的最小瑞雷波相速度,小于各层的最大横波速度.
2) 将区间[VRmin, VSmax]等分为m-1份,由此得到m个节点Vj(j=1, …, m),其中V1= VRmin, Vm= VRmax,令j=1.
3) 令c0=Vj+δi, c1= Vj+1+δi, c2= Vj+2+δi,其中δ为人为给定的常数.利用式 (1) 计算c3,并利用Muller法进行迭代计算.
4) 当函数值F(c3) 的绝对值满足所求精度或达到最大迭代次数时,结束迭代.通过判断,若c3的值是可以接受的,则将其保存.
5) 令j=j+1,继续从步骤3) 开始进行.
如此由欲求的最小频率fmin到最大频率fmax依次进行迭代计算,而每个频率下的求解结果不受其他频率下求得本征值的影响.
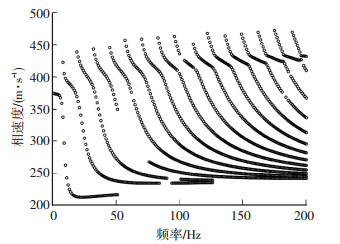
2 漏根现象及其解决方法文献[13]利用Muller法对黏弹性层状介质中瑞雷波的本征值问题进行了求解.在这里首先进行相同的计算,令m=100, δ等于当前频率下各层横波复速度的最大虚部.最大迭代次数设为20,频散方程形式采用快速标量传递算法的频散方程.该频散方程具有较快的计算速度,由于求解黏弹性介质中瑞雷波的本征值问题的计算量较大,因此采用该算法可以在一定程度上加快计算速度.在计算的稳定性上,该算法与其他算法相比没有本质的差别,不影响本文的研究.以表 1中的模型为例 (参数与文献[14]中的例子相同),利用上述方法计算频散曲线如图 1所示.显然,本征值求解过程中发生了较为严重的漏根现象,尤其是在较高频率区域漏根现象更严重.瑞雷波本征值求解中的漏根现象会对瑞雷波的反演应用造成巨大的影响,因此有必要对此进行深入的研究.
| 表 1 黏弹性层状介质的参数 Table 1 The parameters of multilayered medium |
|
图 1 利用旧方法计算得到的频散曲线 Figure 1 Dispersion curves obtained with normal scheme |
本文通过研究发现,增加迭代的最大步数可以得到更多的基阶模 (即第1条频散曲线) 频散点,增大m的取值也可以在一定程度上得到更多的频散点.除此之外,采用其他形式的频散方程后漏根的区域也会有所不同.然而,这些处理措施都不能完全解决本征值求解中的漏根问题.
本文研究被漏掉的根附近的迭代步骤,发现有时迭代收敛到一个远离初值的其他根,有时收敛到局部极小值点,由此发生了漏根.而这两种现象的根本原因在于初值虚部的系数δ选取不合适,通常情况下都是由于δ太大造成的.由此,选取较小的δ进行求解.令c0=Vj+aδi, c1= Vj+1+aδi, c2= Vj+2+aδi,其中δ仍然等于当前频率下各层横波复速度的最大虚部,而令a=0.5.在新的初值下进行搜根,得到的频散曲线如图 2所示.可以看到,在图 1中基阶模以及其他一些模式的部分被漏掉的频散点被成功计算出来.然而,其他一些图 1中原本能够被搜到的频散点反而被漏掉了.再次分析其原因发现这是由于初值虚部选取不够大造成的.而还有一些点在图 1和图 2中都被漏掉,说明在计算这些频散点对应的根时,初值虚部的选取仍然不合适.

|
图 2 将初值虚部减小后计算得到的频散曲线 Figure 2 Dispersion curves obtained with initial values that have smaller imaginary part |
总的来说,分析不同情况下搜根结果发现,为较稳定的得到初值所在区间附近的根,必须使得初值实部和虚部分别与所求的根的实部和虚部差距较小,否则容易发生漏根现象.在以往的搜根方法中,往往固定一个虚部而只改变实部进行搜根,而这造成有时实际的根的虚部与给定的初值虚部差别较大.黏弹性频散函数的光滑性较差,而且Muller法是一个局部优化算法,在这种情况下进行搜根很容易陷入局部极值点而漏根.因此,为得到所有的根,虚部的初值必须要选用多个不同的初值,即对虚部的预估取值区间进行等间距的加密,就如同对实部预估初值[VRmin, VSmax]所进行的等间距加密一样.在区间[0.1, 2.0]上等间距地选取10个a值,分别进行搜根.在实际应用中,a值的个数可以根据实际情况进行选取,个数越多漏根的可能性越小,但是计算量也就越大.Muller法作为一个局部优化算法,会随着迭代次数的增加逐渐收敛于极值点,因此为了尽量提高精度,把迭代次数增加至50次.将每次搜根的结果合在一起,所得的频散曲线如图 3所示.几乎所有的频散点都被成功得到,没有发生图 1和图 2中这种明显的漏根现象.

|
图 3 选取10个不同初值虚部后计算得到的频散曲线 Figure 3 Dispersion curves obtained with 10 initial values that have different imaginary part |
由图 3可以看到,尽管几乎所有的频散点都被成功得到,但是却出现个别明显不应存在的点.例如7 Hz频率的第1个点和8 Hz频率的第2个点.以7 Hz频率的第1个点为例,其对应的本征值为111.59+152.51i, ,尽管虚部的系数远大于其他正常根,但是这个根却可以验证是近似满足频散方程的.也就是说,在搜根中会发生多根现象,尽管不如漏根现象显然,但是对瑞雷波的理论及应用仍然有较大的影响, 而这一现象在以往文献中并没有学者进行研究.由于多出的根是近似满足频散方程的,因此在现有的精度条件下无法从数值上直接剔除,只能根据经验人为去除.通过大量实验发现,多根的虚部通常大于实部,而正常的根通常虚部远小于实部,因此在目前不了解多根形成机理的情况下,可以将虚部大于实部的根去除,采用大量实例验证发现用这种方法一般不会将正常的根错误地去除.由此,总结上述搜根方法得到最终的搜根流程如图 4所示.

|
图 4 求解本征值的计算流程 Figure 4 Flowchart of solving the eigenproblem |
利用图 4中所示的计算流程,计算得到表 1中模型对应的频散曲线和衰减系数曲线如图 5所示.在本例中,采用的最大迭代次数为50,在区间[0.1, 2.0]中等距地选取20个值作为a的取值,m的值取为1 000.由图 5可见,频散曲线和衰减系数曲线上所有的点都成功地计算出来,即使高频下也没有发生漏根现象,而多根现象也没有出现.本文在对其他模型进行计算时用本方法也能够避免漏根和多根现象,只要在频散点较密集时增加a的取值个数并增大m即可.因此,利用图 4中的流程进行计算是可以成功地求解黏弹性层状介质中瑞雷波的本征值问题的.

|
图 5 由图 4中流程计算得到的频散曲线和衰减系数曲线 Figure 5 Dispersion curves and attenuation curves obtained with the flowchart shown in Fig.4 |
1) 分析了Muller法求解黏弹性层状介质中瑞雷波本征值过程中漏根和多根的原因,发现漏根是由于搜根时初值的虚部与真实值差别较大而陷入局部极小值造成的,采用一系列的虚部初值分别进行搜根,将搜根结果结合可以有效避免漏根现象.
2) 发现尽管多根的机理并不清楚,但多根的虚部通常大于实部,而正常的根虚部通常远小于实部,因此采用将虚部大于实部的根剔除的方法可以有效去除多根.
3) 由此给出了本征值求解的具体流程,通过实例计算发现利用该方法可以成功求解黏弹性层状介质中瑞雷波的本征值问题,并避免漏根和多根现象.
| [1] | HASKELL N A. The dispersion of surface waves on multilayered media[J]. Bulletin of the Seismological Society of America, 1953, 43(1): 17-34. http://www.bssaonline.org/content/43/1/17.short |
| [2] | THOMSON W T. Transmission of elastic waves through a stratified solid medium[J]. Journal of Applied Physics, 1950, 21(2): 89-93. DOI: 10.1063/1.1699629 |
| [3] | KNOPOFF L. A matrix method for elastic wave problems[J]. Bulletin of the Seismological Society of America, 1964, 54(1): 431-438. |
| [4] | ABO-ZENA A M. Dispersion function computations for unlimited frequency values[J]. Geophysical Journal Royal Astronomical Society, 1979, 58(1): 91-105. DOI: 10.1111/j.1365-246X.1979.tb01011.x |
| [5] |
凡友华, 刘家琦. 层状介质中瑞雷面波的频散研究[J].
哈尔滨工业大学学报, 2001, 33(5): 577-581.
FAN Youhua, LIU Jiaqi. Research on the dispersion of rayleigh waves in multilayered media[J]. Journal of Harbin Institute of Technology, 2001, 33(5): 577-581. |
| [6] | CHEN Xiaofei. A systematic and efficient method of computing normal modes for multi-layered half-space[J]. Geophysical Journal International, 1993, 115(2): 391-409. DOI: 10.1111/j.1365-246X.1993.tb01194.x |
| [7] | KENNETT B L N. Reflection rays and reverberations[J]. Bulletin of the Seismological Society of America, 1974, 64(6): 1685-1696. |
| [8] |
何耀锋, 陈蔚天, 陈晓非. 利用广义反射-透射系数方法求解含低速层水平层状介质模型中面波频散曲线问题[J].
地球物理学报, 2006, 49(4): 1074-1081.
HE Yaofeng, CHEN Weitian, CHEN Xiaofei. Normal mode computation by the generalized reflection-transmission coefficient method in planar layered half space[J]. Chinese Journal of Geophysics, 2006, 49(4): 1074-1081. DOI: 10.3321/j.issn:0001-5733.2006.04.020 |
| [9] | PEI Donghong, LOUIE J L, PULLAMMANAPPALLIL S K. Improvements on computation of phase velocities of Rayleigh waves based on the generalized R/T coefficient method[J]. Bulletin of the Seismological Society of America, 2008, 98(1): 280-287. DOI: 10.1785/0120070057 |
| [10] | MULLER D E. A method for solving algebraic equations using an automatic computer[J]. Mathematical Tables and Other Aids to Computation, 1956, 10(56): 208-215. DOI: 10.2307/2001916 |
| [11] | YAU L, BEN-ISRAEL A. The Newton and Halley methods for complex roots[J]. The American Mathematical Monthly, 1998, 105(9): 806-818. DOI: 10.2307/2589209 |
| [12] | CAO Zhengliang, DONG Hefeng. Attenuation dispersion of Love waves in a viscoelastic multilayered half-space[C]//Proceedings of the SEG Technical Program Expanded Abstracts 2010. Denver, Colorado: Society of Exploration Geophysicists, 2010: 1924-1928. DOI: 10.1190/1.3513469. |
| [13] |
张凯. 粘弹性介质瑞雷波模拟及其频散曲线反演[D]. 武汉: 中国地质大学, 2011.
ZHANG Kai. Modeling and dispersion curve inversion of Rayleigh waves in viscoelastic media[D]. Wuhan: China University of Geosciences, 2011. |
| [14] | LAI C G, RIX G J. Solution of the Rayleigh eigenproblem in viscoelastic media[J]. Bulletin of the Seismological Society of America, 2002, 92(6): 2297-2309. DOI: 10.1785/0120010165 |
| [15] | CHRISTENSEN R. Theory of viscoelasticity: an introduction[M]. New York: Academic Press, 1971. |
 2017, Vol. 49
2017, Vol. 49


