大型旋转机械中,齿轮箱作为主要传动和连接装置,能否稳定运转直接影响设备整体的工作性能.齿轮箱的振动信号是反应齿轮箱工作状态的主要指标,利用加速度传感器测量振动时域信号,并从信号中提取故障特征,是检测齿轮箱故障最常用的方法.齿轮箱振动信号中包含了齿轮运转中的周期性信号,也包含了大量噪声干扰信号,最终传递出来的振动信号,表现出非平稳的信号模式.对这种信号进行分析,一般采用频域的方法,常用的有短时傅里叶变换、小波分析、EMD等方法[1].如何从信号中定量的提取频域信息,通过频域特征得到故障情况,是本文需要解决的问题.
本文借鉴了压缩传感的思想[2].压缩传感就是从大量的数据信息中将主要信息压缩提取出来,在一定的稀疏度下,压缩的信号可以完整携带原信号的特征,这样不仅减少了数据量,还保证了原有的数据特征,压缩后的信息可以较为完整的重构信号[3-4].应用这一思想,在齿轮箱故障诊断中,将原大量的振动信号,通过一定稀疏度进行压缩,利用压缩后的频域信号进行故障分析[5].
压缩传感中压缩信号的方法有很多,例如:匹配追踪算法[6](MP算法)、基追踪 (BP算法)、正交匹配追踪算法 (OMP算法)、核匹配追踪算法 (KMP算法)、迭代硬阈值 (IHT算法) 等等[7-8].其中OMP算法具有准确性高、操作性强的特点,被广泛应用,尤其适用于齿轮箱振动信号的故障诊断,能很好的分辨出故障,给出及时的诊断结果[9-10].本文通过齿轮箱中齿轮故障信号,运用OMP算法提取特征,分辨不同故障模式,总结了正交匹配追踪算法在定量信号故障诊断中的作用.
1 OMP算法 1.1 理论基础奈奎斯特采样定理指出,采样频率达到信号频率2倍以上,可以精确地重建原始信号.但是采样过程中大量的数据是不重要、冗余的信息,所以考虑是否可以在采样过程中既能保持信号信息,又能用远少于采样定理的采样数目就可以精确或者近似的重建原信号.
信号在某个变换域是稀疏的或可压缩的,可以利用与变换矩阵非相干的测量矩阵将变换系数线性投影为低维观测向量,低维观测向量可以精确地或高概率精确地重建原始高维信号.这一过程就提取了信号的特征,低维观测向量有利于分析特征.OMP算法就是一种简单高效的减少维数方法[11].
1.2 OMP算法OMP (正交匹配追踪法) 是贪婪算法的一种,是寻找最少特征量表示原数据特征的一种方式[12].
OMP (正交匹配追踪) 算法的基本思路是将信号进行迭代分解.首先,在进行每一次迭代过程中,是在过完备原子库中挑选与待分解信号内积最大的原子,把该原子作为当前匹配的原子;然后,从信号中去除与该原子相应的成分,得到残差信号,对残差信号再进行同样的处理,每次迭代后全部原子都进行施密特正交化后再进行分解,使每次迭代中残差与匹配原子都正交;最后,迭代直到残差信号达到一定的精度或达到预定的迭代次数为止,则信号就可以由多个原子的线性组合来逼近表示.
OMP算法具体步骤如下:
Step 1 将给定信号s(t) 在Hilbert空间内投影到过完备原子库{x1, x2, …, xn}的每一个原子上,其中每个向量x1,x2,…,xn可以称为原子 (atom),其长度与被表示信号s(t) 的长度相同,而且这些向量已作为归一化处理,即‖xi‖=1,也就是单位向量长度为1,而且保证施密特正交化.
Step 2 计算信号s(t) 与过完备原子库矩阵中每一列 (原子) 的内积,内积最大的就是最匹配的原子,设为gi.
| $ {g_i} = \mathop {\sup }\limits_{i \in \left( {1,2, \cdots ,k} \right)} \left| { < s\left( t \right),{x_i} > } \right|. $ | (1) |
Step 3 迭代.
第1步迭代,选择信号s(t) 投影最大的原子表示为g1,A1是它们的内积,s1(t) 是残差.信号被分解为
| $ s\left( t \right) = {A_1}{g_1} + {s_1}\left( t \right). $ | (2) |
第2步迭代,对第1步的残差s1(t) 做相同计算.
第i步迭代,由稀疏度或残差大小决定,残差信号被分解为
| $ s\left( t \right) = {A_i}{g_i} + {s_{i + 1}}\left( t \right). $ | (3) |
每次迭代的结果代入,OMP算法将信号分解为
| $ s\left( t \right) = \sum\limits_{i = 0}^m {{A_i}{g_i} + {s_{i + 1}}\left( t \right)} , $ | (4) |
其中,残差信号表达式为
| $ {s_{i + 1}}\left( t \right) = {s_i}\left( t \right) - {A_i}{g_i}. $ | (5) |
内积表达式为
| $ {A_i} = \int_{ - \infty }^\infty {{s_i}\left( t \right){g_i}{\rm{d}}t} . $ | (6) |
式 (4) 就是正交匹配追踪算法信号分解表达式.
1.3 齿轮箱故障诊断中的OMP算法稀疏度的概念,应用在齿轮箱故障诊断中就是振动信号分解迭代的次数,即选择稀疏度数量的特征,就可以近似表达信号,例如稀疏度为32,本文就将信号迭代分解32次,选出32个主特征.
在齿轮箱故障诊断中的OMP算法,本文选取的原子库是由正交的傅里叶变换基组成的,即每个原子都是一个正交傅里叶变换,与每个原子做内积,就实现了时域向频域的映射,将时域信号转化为频域信号,每步分解过程中,记录下内积最大点的频率和幅值,这一过程如图 1所示.

|
图 1 OMP算法的映射 Figure 1 OMP algorithm mapping |
应用信号的重构性,通过验证主特征值恢复的振动信号与原信号对比可知,重构性能达到90%以上, 保证了信号的分解能近似表达原信号.
2 齿轮磨损故障OMP算法应用齿轮箱中齿轮磨损故障是常见故障,诊断齿轮是否磨损,磨损的程度如何可以第一时间掌握齿轮状态,根据实际情况进行维修,直接影响整个齿轮箱的运行情况,所以故障检测和故障分类是非常有必要的[13-15].
齿轮箱的振动信号的测量通过是旋转机械振动故障试验平台,该试验台可变速模拟在不同转速条件下的故障特征,该试验台的组成为电力驱动系统、齿轮箱及磁粉制动器.
1) 电力驱动系统.变频异步电动机其调速范围是0~1 500 r/min.
2) 齿轮箱.齿轮箱只有一对齿轮啮合形成单级传动,即为一级齿轮箱,且该齿轮箱具有减速的特性.
3) 磁粉制动器.对齿轮箱施加负载,额定转矩是5 N·M.
4) 加速度传感器.测量振动信号,安装在齿轮箱轴承根部,保证信号的准确性.
齿轮箱设定转速为800~1 500 r/min,分别测量800、1 000、1 200、1 500 r/min不同转速下的实验数据,实验装置如图 2所示.齿轮磨损的情况如图 3所示是50%齿轮磨损的情况.

|
图 2 振动试验台示意 Figure 2 Vibration test bed |

|
图 3 齿轮磨损50%示意 Figure 3 Wear of gear of 50% |
齿轮故障诊断的步骤如下:
1) 信号采集.通过旋转机械振动实验台进行信号采集,在已知齿轮正常情况、25%磨损、50%磨损、75%磨损、100%磨损情况下,分别多次测量齿轮箱的振动情况,在3.2 s内采样8 192个时域信号.将得到的振动信号分别记为0Q (正常情况)、1Q、2Q、3Q、4Q,具体对应关系见表 1.
| 表 1 各种故障表示的对应关系 Table 1 Corresponding relation of various fault |
在已知发生上述各种故障的信号数据,记录一组作为判断故障的标准, 即0Q~4Q这5个已知故障数据组成.
再实测一组包含0Q~4Q故障的信号,作为验证信号,将两组信号进行比对.
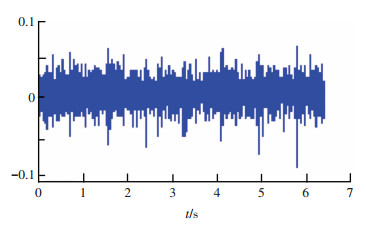
2) 信号处理.在时域下,实测齿轮箱800 r/min的振动信号如图 4所示.将振动信号进行OMP处理,根据稀疏度确定投影到频域的数量,本文选择稀疏度为32,则得到32个频域值组成的频域表达.
|
图 4 实测齿轮箱800 r/min振动信号 Figure 4 Measured vibration signals of gearbox 800 r/min |
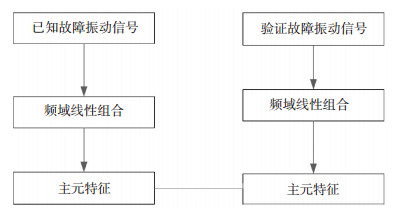
信号分解流程图如图 5所示,将两组信号分解,获得的频域值和该频域值的幅值是信号的特征信息,信号被分解为32个频域的线性表达,信号的主要信息压缩在32个频域值中,并准备对两组信号进行比较.
|
图 5 振动信号诊断流程 Figure 5 The flow chart of vibration signal diagnosis |
3) 信号主元特征选取.对信号分解后频域值的计算分析,以800 r/min转速为例 (见表 2),可以看到前3组频域包含的信息就已经占到总体的95.2%,而前16组的96.8%和前32组的97.6%与前3组的差别不大,说明后面的频域值包含的信息很少,通过主元分析法的原理可以知道,选择前3组可以近似代表整个数据,进行计算可以大大减少计算量.
| 表 2 主成分分析结果 Table 2 Principal component analysis results |
OMP算法计算的结果,会完整显示出信号在频域中的特征,主元就是幅值最大的频域点,前3组幅值基本涵盖了信号的主要特征
4) 信号比较.将已知故障振动信号的0Q~4Q故障模式,作为参照,运用OMP算法后将前3个原子的频率值记录下来,3个主元频率值见表 3.
| 表 3 两组振动信号主元频域值 Table 3 Two sets of principal vibration signal frequency domain values |
将实测包含0Q~4Q故障的信号作为验证信号,进行OMP算法计算后进行比较,频域值也如表 3所示.
a) 用频域值位置判断.可以看到两组信号0Q,1Q,4Q的频域值都是一致的,说明发生同一种故障,例如可以看到表 4中显示两组振动信号的1Q前3个原子的点,即频率值为965,7 229的点是完全相同的,说明故障特征完全一致,判断为同一种故障.
| 表 4 2Q, 3Q故障幅值比较 Table 4 2Q, 3Q fault amplitude comparison |
b) 用幅值判断.从表 3看到,两组信号的2Q,3Q频域值位置难以区分,本文还需要通过幅值来判断.
2Q,3Q幅值相比较可以判断出不同的故障.用两组的主元特征,对应频率幅值相减,得到3个差值,取3个差值绝对值的和,得到4个数据,所得结果见表 4.同一行中与已知故障状态数值相差较小的,就说明故障与该列的故障匹配,可以判断故障属于这一类.例如第2行的第2列,与第2行的第1列对比是较小的,说明两个信号的特征是一致的,可以判断发生了3Q故障.
通过对频域位置和幅值的判断,可以明确的判断出齿轮箱运行状态和故障类型,达到了故障诊断的目的.
3 结论1) OMP算法对齿轮箱进行故障诊断,定量的将时域振动信号映射到频域上,然后提取主元特征值,进行故障识别,对振动信号定量分析,进行故障诊断.
2) OMP算法对齿轮箱的故障诊断结果,通过频率值和幅值的2次比较,不仅得出了准确的故障诊断,而且明确了故障分类,对齿轮箱的运行状态进行了全面检测.
| [1] |
丁康, 朱小勇, 陈亚华. 齿轮箱典型故障振动特征与诊断策略[J].
振动与冲击, 2001, 20(3): 7-12.
DING Kang, ZHU Xiaoyong, CHEN Yahua. The vibration characteristics of typical gearbox faults and its diagnosis plan[J]. Journal of Vibration and Shock, 2001, 20(3): 7-12. DOI: 10.3969/j.issn.1000-3835.2001.03.003 |
| [2] | CHEN Xuefeng, DU Zhaohui, LI Jimeng, et al. Compressed sensing based on dictionary learning for extracting impulse components[J]. Signal Processing, 2014, 96: 94-109. DOI: 10.1016/j.sigpro.2013.04.018 |
| [3] |
李树涛, 魏丹. 压缩传感综述[J].
自动化学报, 2009, 35(11): 1369-1377.
LI Shutao, WEI Dan. A survey on compressive sensing[J]. ACTA Automatica Sinica, 2009, 35(11): 1369-1377. DOI: 10.3724/SP.J.1004.2009.01369 |
| [4] | DUARTE M F, BARANIUK R G. Spectral compressive sensing[J]. Appliedand Computational Harmonic Analysis, 2013, 35(1): 111-129. DOI: 10.1016/j.acha.2012.08.003 |
| [5] | LI Wei, ZHU Zhencai, JIANG Fang, et al. Fault diagnosis of rotating machinery with a novel statistical feature extraction and evaluation method[J]. Mechanical Systems and Signal Processing, 2015, 50-51: 414-426. DOI: 10.1016/j.ymssp.2014.05.034 |
| [6] |
杨海蓉, 张成, 丁大为, 等. 压缩传感理论与重构算法[J].
电子学报, 2011, 39(1): 142-148.
YANG Hairong, ZHANG Cheng, DING Dawei, et al. The theory of compressed sensing and reconstruction algorithm[J]. ACTA Electronica Sinica, 2011, 39(1): 142-148. |
| [7] | YANG Hongyu, MATHEW J, MA Lin. Fault diagnosis of rolling element bearings using basis pursuit[J]. Mechanical Systems and Signal Processing, 2005, 19(2): 341-356. DOI: 10.1016/j.ymssp.2004.03.008 |
| [8] | BLUMENSATH T, DAVIES M E. Iterative hard thresholding for compressed sensing[J]. Applied and Computational Harmonic Analysis, 2009, 27(3): 265-274. DOI: 10.1016/j.acha.2009.04.002 |
| [9] |
赵发刚, 陈进, 董广明. 匹配追踪在齿轮故障诊断中的应用[J].
上海交通大学学报, 2009, 43(6): 910-913.
ZHAO Fagang, CHEN Jin, DONG Guangming. Application of matching pursuit in fault diagnosis of gear[J]. Journal of Shanghai Jiaotong University, 2009, 43(6): 910-913. |
| [10] |
孟庆丰, 范虹, 孟祺, 等. 匹配追踪信号分解与往复机械故障特征提取技术研究[J].
西安交通大学学报, 2001, 35(7): 696-699.
MENG Qingfeng, FAN Hong, MENG Qi, et al. Extraction of fault features in reciprocating machinery based on matching pursuits[J]. Journal of Xi'an Jiaotong University, 2001, 35(7): 696-699. DOI: 10.3321/j.issn:0253-987X.2001.07.009 |
| [11] | CUI Lingli, WANG Jing, LEE S C. Matching pursuit of an adaptive impulse dictionary for bearing fault diagnosis[J]. Journal of Sound and Vibration, 2014, 333(10): 2840-2862. DOI: 10.1016/j.jsv.2013.12.029 |
| [12] |
刘冰, 付平, 孟升卫. 基于正交匹配追踪的压缩感知信号检测算法[J].
仪器仪表学报, 2010(9): 1959-1964.
LIU Bing, FU Ping, MENG Shengwei. Compressive sensing signal detection algorithm based on orthogonal matching pursuit[J]. Chinese Journal of Scientific Instrument, 2010(9): 1959-1964. |
| [13] |
邹今春, 沈玉娣. 变工况齿轮箱故障诊断方法综述[J].
机械传动, 2012, 36(8): 124-127.
ZOU Jinchun, SHEN Yudi. Review of gearbox fault diagnosis techniques under variable conditions[J]. Journal of Mechanical Transmission, 2012, 36(8): 124-127. DOI: 10.16578/j.issn.1004.2539.2012.08.028 |
| [14] |
张玉. 基于振动信号分析的齿轮箱故障诊断[J].
仪器仪表与分析监测, 2011(1): 20-24.
ZHANG Yu. Diagnosis for the failure of gearbox based on analysis of vibration signal[J]. Instrumentation Analysis Monitoring, 2011(1): 20-24. DOI: 10.3969/j.issn.1002-3720.2011.01.006 |
| [15] |
许雪贵, 徐文琴. 齿轮箱故障的振动机理与故障特征研究[J].
机械制造与自动化, 2012, 41(4): 74-77.
XU Xuegui, XU Wenqin. Vibration mechanism and fault signature of gear case[J]. Jiangsu Machine Building & Automation, 2012, 41(4): 74-77. DOI: 10.3969/j.issn.1671-5276.2012.04.025 |
 2017, Vol. 49
2017, Vol. 49


