射弹装备于直升机、潜艇和水面舰艇的火炮系统中,可以消灭浅海鱼雷,保护潜艇和水面舰艇免受鱼雷的攻击.掌握射弹入水弹道对成功击中目标至关重要,因此对高速射弹入水弹道特性的研究具有较大的意义.
文献[1-2]对普通子弹入水问题开展了相关的实验研究,分析了子弹入水的弹道变化与速度衰减规律.文献[3]利用气体炮开展了不同头型弹体在35 ~ 160 m/s速度范围内的入水实验,研究了3种头型弹体的弹道稳定性.文献[4]基于武器研发的应用背景,开展了在98.6~1 346.6 m/s的速度范围内高速钢球垂直入水实验,对球体入水弹道特性进行了研究.文献[5]开展了以352 m/s速度入水的小型运动体入水实验研究,得出了空化现象对弹体入水弹道的影响规律.文献[6]对不同头型弹体水平入水问题进行了实验与数值研究,给出了以空化数为变量的阻力系数方程.文献[7]利用嵌入的惯性测量单元对不同头型的轴对称细长体垂直和倾斜入水过程的受力情况、速度变化规律与弹道特性进行了研究.文献[8]利用Tait状态方程对高速射弹入水过程进行了数值模拟.文献[9]对不同头型运动体高速入水的空泡形态进行了数值模拟研究,得到不同头型条件下高速入水运动参数及空泡形态发展规律和流场的速度分布规律.文献[10]基于均质平衡流理论,研究了不同质心位置的超空泡射弹尾拍运动特性.文献[11]采用二维轴对称模型,并利用动网格技术对不同初始空化数和长细比的水下射弹运动过程中的模型阻力系数随时间的变化规律进行了数值模拟研究.文献[12]对入水弹体进行了详细的受力分析,并研究了各种力对入水空泡形状与发展规律的影响.文献[13]对入水问题研究现状进行了综述,包括实验、理论和数值研究.
目前国内以动力学建模的方法研究高速运动体入水弹道的相关文献较少,大多不涉及运动体从空气中穿越水面进入水中的过程,仅针对运动体在水中自由行进的过程[14].对于尾拍过程的动力学建模常常与整个运动过程分开进行,通过固定弹体头部位置且不考虑弹体速度的衰减来简化模型的建立,而实际情况下弹体尾拍运动时速度是衰减的,且弹体作曲线运动,所以之前对尾拍运动模型的简化无法反应弹体的真实运动情况.本文对弹体在入水过程中的受力情况进行了分析,建立了射弹纵向运动的动力学模型,整个建模过程依据弹体的真实运动状况,考虑了尾拍运动时弹体速度的衰减与方向的偏转,对弹体模型以不同扰动角速度入水过程进行了弹道仿真,研究了弹体入水轨迹、速度、俯仰角和俯仰角速度的变化规律,并分析了扰动角速度对其的影响.
1 弹体运动方程本文采用如图 1所示的截锥头弹体模型.

|
图 1 弹体模型示意 Figure 1 Schematic of projectile model |
为确定弹体运动位置与姿态,本文坐标系选取各轴与地球固连的地面坐标系OXY和各轴与弹体固连的弹体坐标系oxy.
文中用X,Y表示弹体运动过程中重心在地面坐标系中的两个坐标,V表示弹体质心处的速度矢量,Vx,Vy表示V在弹体坐标系中的两个速度分量,俯仰角θ表示弹体坐标系ox轴与地面坐标系OX轴之间的夹角,当弹体头部偏向OX轴之上时为正,ω表示弹体的旋转角速度,α表示速度矢量V与弹体坐标系ox轴的夹角,当V偏向ox轴上方时为正.
设弹体在坐标系ox方向所受合力为Fx,oy方向所受合力为Fy,弹体所受合力矩为M, 弹体的质量为m,转动惯量为J,根据鱼雷航行力学有关知识可得弹体纵向运动方程:
| $ \left\{ \begin{array}{l} \dot \theta = \omega, \\ \dot X = {\mathit{\boldsymbol{V}}_x}\cos \theta - {\mathit{\boldsymbol{V}}_y}\sin \theta, \\ \dot Y = {\mathit{\boldsymbol{V}}_x}\sin \theta + {\mathit{\boldsymbol{V}}_y}\cos \theta, \\ \mathit{\boldsymbol{V}} = \sqrt {\mathit{\boldsymbol{V}}_x^2 + \mathit{\boldsymbol{V}}_y^2}, \\ \alpha = \arctan \frac{{{\mathit{\boldsymbol{V}}_y}}}{{{\mathit{\boldsymbol{V}}_x}}}, \\ {{\mathit{\boldsymbol{\dot V}}}_x} = {F_x}/m \times \cos \theta + {F_y}/m \times \sin \theta, \\ {{\mathit{\boldsymbol{\dot V}}}_y} = {F_y}/m \times \cos \theta - {F_x}/m \times \sin \theta, \\ \mathit{\boldsymbol{M}} = J\dot \omega . \end{array} \right. $ |
在撞水之前,弹体主要受到重力G和空气阻力的作用.撞水后的流动形成初期阶段,作用在弹体头部的作用力对质心转矩的积累使弹体的俯仰角持续增大,在极短时间内,俯仰角速度增加为一个稳定值直至发生尾拍.这里为研究简便则不去考虑俯仰角速度的形成原因,而把它与弹体受环境影响的初始扰动角速度一起,简化为弹体的扰动角速度.高速射弹入水在没有发生尾拍之前只有截锥头平面是沾湿的,其余部分被空泡包裹着或裸露在空气中.弹体在空泡中的部分所受到气体的摩擦力同在水中的摩擦力相比可以略去不计.由于弹体被空泡包裹,所以失去了浮力.因此在没发生尾拍前弹体仅受重力G与截锥头平面所受水对其的作用力即升力FL,阻力FD,转矩Mc.
阻力、升力与转矩系数是空化器形态和攻角的函数:
| $ \begin{array}{*{20}{c}} {{C_{\rm{D}}} = {C_{x0}}\left( {1 + \sigma } \right) \times {{\cos }^2}\alpha, }\\ {{C_{\rm{L}}} = {C_{x0}}\left( {1 + \sigma } \right) \times \cos \alpha \times \sin \alpha, }\\ {{C_{\rm{M}}} = 0, } \end{array} $ |
其中σ为空化数,其表达式为
| $ \sigma = \frac{{{P_0} - {P_c}}}{{\frac{1}{2}\rho {v^2}}}. $ |
式中:p0为环境参考压力,一般取无穷远处压力;pc为空泡中气体压力;ρ为水的密度,由于空泡内部是低压气体和水蒸气的混合物,所以pc可以近似取当前温度下水的饱和蒸汽压pv=3 540 Pa.Cx0为空化器在σ=0时的阻力系数,对于圆盘空化器,通过试验获得Cx0=0.82,所以截锥头平面的阻力系数为
| $ {C_{x0}} = {\left( {\frac{d}{D}} \right)^2} \times 0.82. $ |
空化器受到的升力和阻力为:[15]
| $ \begin{array}{l} {F_{\rm{L}}} = \frac{1}{2}\rho V_{\rm{c}}^2{S_{{\rm{cav}}}}{C_{\rm{L}}}, \\ {F_{\rm{D}}} = \frac{1}{2}\rho V_{\rm{c}}^2{S_{{\rm{cav}}}}{C_{\rm{D}}}, \end{array} $ |
式中Scav为空化器的最大横截面积.
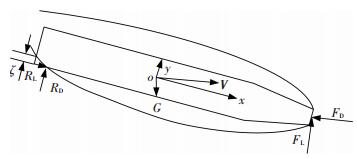
当超空泡射弹高速运动时,弹体尾部会因为很小的扰动而与空泡壁面产生连续的撞击作用,本文将这种作用称为尾拍,弹体尾拍受力情况如图 2所示,其所受阻力为弹头阻力与尾部所受阻力的合力.根据动量守恒原理可以求出尾拍升力RL和尾拍阻力RD为
|
图 2 弹体尾拍时的受力 Figure 2 Force diagram of projectile tail slap |
| $ \left\{ \begin{array}{l} \left. \begin{array}{l} {R_{\rm{D}}} = 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\ {R_{\rm{L}}} = 0, \end{array} \right\}\zeta \le 0;\\ \left. \begin{array}{l} {R_{\rm{D}}} = \rho {A_1}{V^2}\left( {1 - \cos \theta } \right), \;\\ {R_{\rm{L}}} = \rho {A_1}{V^2}\sin \theta, \end{array} \right\}\zeta \ge 0. \end{array} \right. $ |
式中:经验常数λ=0.5;η为空泡轴线与弹体轴线之间的夹角;ζ为弹体尾部浸入液体的深度;A1=λζD为弹体尾部浸入液体边界层的特征面积,设弹体尾部空泡半径为Rct,则可以得到ζ的计算公式为
| $ \zeta = L\sin \theta + \frac{D}{2}\cos \theta - {R_{{\rm{ct}}}}. $ |
将弹体的受力方程代入到弹体的纵向运动方程,得到了高速射弹入水过程的动力学方程.
撞水前的动力学方程为
| $ \left\{ \begin{array}{l} \dot X = {\mathit{\boldsymbol{V}}_x}\cos \theta - {\mathit{\boldsymbol{V}}_y}\sin \theta, \\ \dot Y = {\mathit{\boldsymbol{V}}_x}\sin \theta + {\mathit{\boldsymbol{V}}_y}\cos \theta, \\ \dot \theta = \omega, \\ {{\mathit{\boldsymbol{\dot V}}}_x} = \left( { - mg\sin \theta - {F_d}} \right)/m \times \cos \theta + \\ \;\;\;\;\;\;\;\left( { - mg\cos \theta } \right)/m \times \sin \theta, \\ {{\mathit{\boldsymbol{\dot V}}}_y} = \left( { - mg\cos \theta } \right)/m \times \cos \theta - \\ \;\;\;\;\;\;\;\left( { - mg\sin \theta - {F_d}} \right)/m \times \sin \theta, \\ \dot \omega = 0. \end{array} \right. $ |
撞水后的动力学方程为
| $ \left\{ \begin{array}{l} \dot X = {\mathit{\boldsymbol{V}}_x}\cos \theta - {\mathit{\boldsymbol{V}}_y}\sin \theta, \\ \dot Y = {\mathit{\boldsymbol{V}}_x}\sin \theta - {\mathit{\boldsymbol{V}}_y}\cos \theta, \\ \dot \theta = \omega, \\ {{\mathit{\boldsymbol{\dot V}}}_x} = \left( { - mg\sin \theta - {R_{\rm{D}}} - \sqrt {F_{\rm{D}}^2 + F_{\rm{L}}^2} } \right)/m \times \cos \theta + \\ \;\;\;\;\;\;\;\left( { - mg\cos \theta - {R_{\rm{L}}} \times {\rm{sign}}\left( \alpha \right)} \right)/m \times \sin \theta, \\ {{\mathit{\boldsymbol{\dot V}}}_y} = \left( { - mg\cos \theta - {R_{\rm{L}}} \times {\rm{sign}}\left( \alpha \right)} \right)/m \times \cos \theta - \\ \;\;\;\;\;\;\;\left( { - mg\sin \theta - {R_{\rm{D}}} - \sqrt {F_{\rm{D}}^2 + F_{\rm{L}}^2} } \right)/m \times \sin \theta, \\ J\dot \omega = {R_{\rm{L}}} \times {\rm{sign}}\left( \alpha \right) \times x + {R_{\rm{D}}} \times D/2 \times {\rm{sign}}\left( \alpha \right). \end{array} \right. $ |
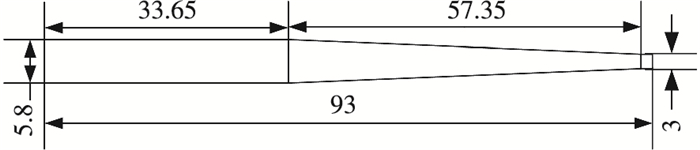
为检验仿真结果的可靠性,将在现有实验条件下所进行实验的结果与采用相同弹体模型与初始条件的弹道仿真结果进行了对比.其中所采用的弹体模型尺寸如图 3所示,长度单位为mm,弹体密度为7.85 kg/m3.实验设备主要由水槽、发射系统、保护及回收系统和外部测试系统组成,如图 4所示为射弹实验整体图.图中:水槽基本尺寸为1.5 m×0.8 m×0.9 m;发射系统主要包括高压氮气瓶、轻气炮、发射管及触发装置.保护及回收系统中,水槽的迎弹侧面由2块后部钉有钢板的木板组成,水槽底部铺有粘有缓冲泡沫的钢板;外部测试系统主要包括高速摄像系统和照明系统两部分.
|
图 3 弹体模型尺寸 Figure 3 Dimensions of projectile model |

|
图 4 射弹实验整体 Figure 4 Whole schematic of water entry experiment |
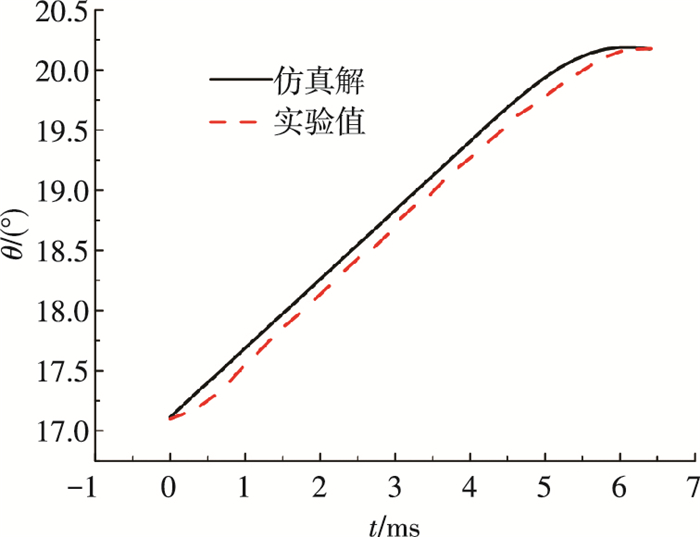
本文实验采用高速照相机以5 000 fps的速度对射弹入水后的运动过程进行拍摄.对比实验中弹体的入水角度为17°,弹体与水面接触时的速度为116 m/s.将通过图片后处理软件得到的弹体入水半个弹长时所具有的角速度作为仿真的初始扰动角速度,将弹体撞水瞬间作为0时刻.图 5为相同时间间隔的弹体入水姿态图,图 6为弹体入水后X方向与Y方向位移对比图,图 7为弹体速度变化对比图,图 8为弹体俯仰角度对比图.从图中可以看出,仿真结果与试验数据吻合度较好,在接近视场末端,弹体发生尾拍,俯仰角度有所下降.实验与仿真结果俯仰角度略有差异,主要因为弹体从轻气炮筒射出时有一定的扰动,并且撞水期间因弹体头部左右部分触水面积不对称引起俯仰角速度有一个累积增大的过程,从图 8的实验值变化曲线可以看出,撞水期间俯仰角度曲线的斜率有一个缓慢的增加过程,这一过程受发射环境影响较大,且涉及复杂的多相流动,很难给出较准确的动力学方程.本文建模没有考虑这一过程中角速度的变化过程,直接给出变化后的角速度值,因为这一过程历经的时间极短且对之后弹体的运动状态没有影响.撞水阶段后且未发生尾拍前,俯仰角度的实验值与仿真解均为线性增加,说明此过程中俯仰角速度保持一个定值,证实了所采用的动力学模型的合理性.观察图 5所示的入水姿态变化图,在该视角下所观察到的弹体的长度没有变化,说明了可以在动力学建模的过程中,忽略弹体的偏航而只研究弹体在纵向平面 (图 5所示平面) 内的弹道变化特性.

|
图 5 弹体入水姿态 Figure 5 Attitude of projectile water entry |

|
图 6 射弹入水后X方向与Y方向位移 Figure 6 Displacement of X and Y direction after water entry |

|
图 7 射弹入水后速度变化曲线 Figure 7 Change of velocity after water entry |
|
图 8 射弹入水后俯仰角度变化曲线 Figure 8 Change of pitch angular velocity after water entry |
本文采用0.7、0.9、1.1 (°)/ms这3种扰动角速度,利用弹体模型和仿真方法的实验建立的动力学模型对高速射弹入水弹道进行仿真,研究扰动角速度对弹体水中弹道特性的影响,其中弹体的密度为7.85 g/cm3,转动惯量为1.057×10-5 kg·m2.弹体的初始速度为800 m/s,入水角度为30°.设弹体头部前截面圆心处为坐标原点,水面在坐标原点向下25 mm处.
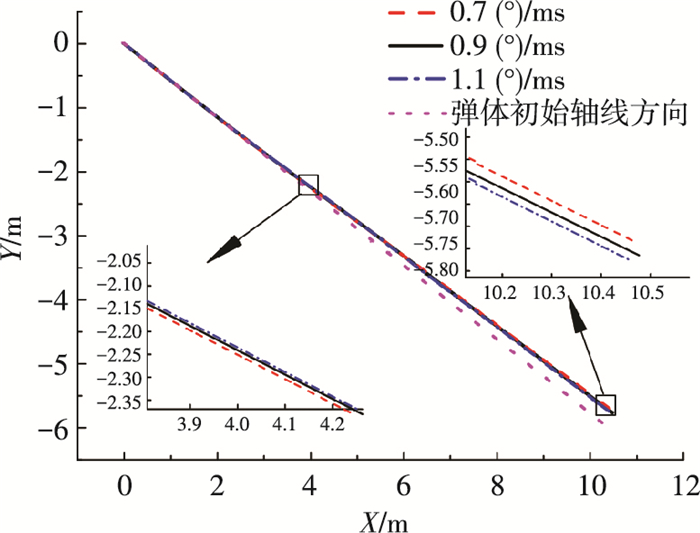
图 9为高速射弹入水轨迹对比图.起初弹体扰动角速度越小入水深度越深,之后扰动角速度越大入水深度越深,但从整体上观察,初始扰动角速度对弹体重心的运动轨迹影响不大.高速入水时,弹头的触水侧会产生一个低压区,使弹头向下偏转,弹体所受合力偏离弹体轴线方向向上,使弹体入水轨迹偏离弹体初始轴线方向向上.
|
图 9 不同扰动角速度入水轨迹对比 Figure 9 Comparison of trajectory of water entry |
图 10为高速射弹入水弹体重心水平方向与竖直方向的速度对比图,不同扰动角速度的速度变化曲线几乎一致,初始扰动角速度只是在微小范围内影响到弹体的俯仰角从而影响到弹体头部阻力和升力的受力方向而没有影响其大小,对速度曲线的整体变化没有影响.

|
图 10 不同扰动角速度弹体X方向与Y方向速度对比 Figure 10 Comparison of velocity of X and Y direction |
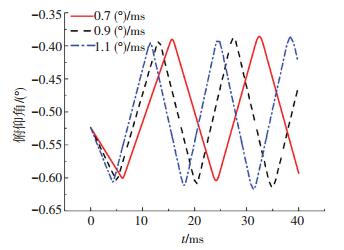
图 11为高速射弹入水弹体俯仰角对比图,在前40 ms内初始扰动角速度为1.1 (°)/ms的弹体共发生了6次尾拍,扰动角速度为0.9 (°)/ms的弹体共发生了5次尾拍,扰动角速度为0.7 (°)/m的弹体共发生了4次尾拍,初始扰动角速度最大的弹体在空泡腔内运行的时间最短因此最先发生尾拍,且相同时间内的尾拍次数较多.3条曲线的形状和变化趋势相同,且俯仰角两个方向的最大值相近,说明不同初始扰动角速度的弹体俯仰角随时间的变化规律相同.
|
图 11 不同扰动角速度俯仰角对比 Figure 11 Comparison of pitch angular |
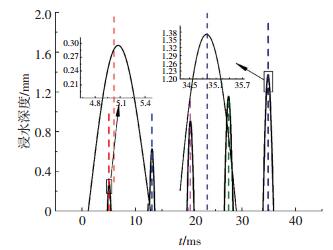
图 12为高速射弹入水俯仰角速度对比图,扰动角速度越小弹体在空泡腔内运动的时间就越长,尾拍后的俯仰角速度随尾拍次数的增加先变大,然后增幅逐渐减小;或者俯仰角速度随尾拍次数的增加变大后略微减小.产生这种现象的原因是当弹体轴线与空泡轴线的夹角达到最大值时,弹尾浸入水中的深度达到最大值,而俯仰角速度是相对于地面坐标系而不是相对于空泡轴线,此时弹体的俯仰角速度不一定减小为0,它可能还在继续减小或向弹体尾部拍回空泡的方向增加.图 13为扰动角速度为0.9 (°)/ms的弹体尾部浸入水中深度曲线图,图中虚线对应时刻为弹体尾拍过程中俯仰角速度为0的时刻,结合该图对尾拍前后俯仰角速度的变化原因进行详细地分析.其中前3次尾拍过程,弹体尾部浸入深度达到最大值之前俯仰角速度便减小为0,且随着尾拍次数的增加提前时间越来越短,这是因为虽然俯仰角速度减小为0,弹体尾部相对于空泡壁面的速度并没有减小为0,而是继续相对运动一段时间后才减小为0,因此弹体尾部浸入水中的深度还会继续增加直到相对速度为0时,达到最大值,此时俯仰角速度已经朝着相反的方向从0增大到某一值,在弹体尾部弹回空泡的过程中俯仰角速度还将继续增加,使前3次尾拍后角速度增加.同样,第4次尾拍俯仰角速度为0时弹体尾部浸入深度几乎达到最大值,所以尾拍前后俯仰角速度的大小几乎没有改变,第5次尾拍弹体尾部浸入深度达到最大值时,弹体的俯仰角速度还未减小为0,弹体尾部弹回空泡过程中,俯仰角速度才逐渐减小为0,因此尾拍后的角速度有所减小.

|
图 12 不同扰动角速度俯仰角速度对比 Figure 12 Comparison of pitch angular velocity |
|
图 13 0.9 (°)/ms扰动角速度弹尾浸水深度曲线 Figure 13 Immersion depth of projectile tail with turbulent angular velocity of 0.9 (°)/ms |
图 14为高速射弹尾拍时弹体尾部浸入水中深度对比图,随着尾拍次数的增加,弹体尾部浸入水中的深度逐渐增大,尾拍所持续的时间也逐渐增长,虽然不同的扰动角速度使弹体具有不同的俯仰角速度,但每次尾拍时弹体尾部浸入水中的深度却相差不大,扰动角速度大的尾部浸入水中略微深些.

|
图 14 不同扰动角速度弹体尾部浸水深度对比 Figure 14 Comparison of immersion depth of projectile tail |
1) 弹体高速入水时,弹头的触水侧会形成一个低压区,使弹头向下偏转,弹体所受合力偏离弹体轴线方向向上,因此运动轨迹偏离弹体初始轴线方向向上.不同扰动角度弹体的运动轨迹基本趋于一致,水平方向和竖直方向的速度变化曲线均随时间逐渐趋于平缓.
2) 扰动角速度越大,相同时间内弹体发生尾拍的次数就越多,尾拍发生得就越早,不同初始扰动角速度的弹体俯仰角随时间的变化规律相同.
3) 弹体轴线与空泡轴线的夹角达到最大值时,弹尾浸入水中的深度达到最大值,而俯仰角速度是相对于地面坐标系而不是相对于空泡轴线,此时弹体的俯仰角速度不一定减小为0,它可能还在继续减小或向弹体尾部拍回空泡的方向增加,这使得尾拍后的俯仰角速度随尾拍次数的增加先变大,然后增幅逐渐减小,或者俯仰角速度随尾拍次数的增加变大后略微减小.扰动角速度越小,弹体在空泡腔内运行的时间就越长.
4) 随着尾拍次数的增加,弹体尾部浸入水中的深度逐渐增大,尾拍所持续的时间也逐渐增长,不同的扰动角速度尾拍时弹体尾部浸入水中的深度相差不大.
| [1] |
顾建农, 张志宏, 范武杰. 旋转弹丸入水侵彻规律[J].
爆炸与冲击, 2005, 25(4): 341-349.
GU Jiannong, ZHANG Zhihong, FAN Wujie. Experimental study on the penetration law for a rotating pellet entering water[J]. Explosion and Shock Waves, 2005, 25(4): 341-349. DOI: 10.3321/j.issn:1001-1455.2005.04.010 |
| [2] |
乔相信, 阎思江, 万仁毅. 弹丸入水空泡实验和入水弹道速度计算[J].
沈阳理工大学学报, 2007, 26(6): 51-53.
QIAO Xiangxin, YAN Sijiang, WAN Renyi. The vacuole experiment and computation of the trajectory velocity when the projectile entering into water[J]. Transactions of Shenyang Ligong University, 2007, 26(6): 51-53. DOI: 10.3969/j.issn.1003-1251.2007.06.014 |
| [3] |
张伟, 郭子涛, 肖新科, 等. 弹体高速入水特性实验研究[J].
爆炸与冲击, 2011, 31(6): 579-584.
ZHANG Wei, GUO Zitao, XIAO Xinke, et al. Experimental investigations on behaviors of projectile high-speed water entry[J]. Explosion and Shock Waves, 2011, 31(6): 579-584. |
| [4] | CHARTERS A C. The aerodynamic performance of small spheres from subsonic to high supersonic velocities[J]. Journal of the Aeronautical Sciences (Institute of the Aeronautical Sciences), 1945, 12(4): 468-476. DOI: 10.2514/8.11287 |
| [5] | SHI Honghui, TAKAMI T. Hydrodynamic behavior of an underwater moving body after water entry[J]. Acta Mechanica Sinica, 2001, 17(1): 35-44. DOI: 10.1007/bf02487768 |
| [6] | GUO Zitao, ZHANG Wei, XIAO Xinke, et al. An investigation into horizontal water entry behaviors of projectiles with different nose shapes[J]. International Journal of Impact Engineering, 2012, 49: 43-60. DOI: 10.1016/j.ijimpeng.2012.04.004 |
| [7] | BODILY K G, CARLSON S J, TRUSCOTT T T. The water entry of slender axisymmetric bodies[J]. Physics of Fluids, 2014, 26(7): 66-74. DOI: 10.1063/1.4890832 |
| [8] | NEAVES M D, EDWARDS J R. All-speed time-accurate underwater projectile calculations using a preconditioning algorithm[J]. Journal of Fluids Engineering, 2006, 128(2): 284-296. DOI: 10.1115/1.2169816 |
| [9] |
马庆鹏, 魏英杰, 王聪, 等. 不同头型运动体高速入水空泡数值模拟[J].
哈尔滨工业大学学报, 2014, 46(11): 24-29.
MA Qingpeng, WEI Yingjie, WANG Cong, et al. Numerical simulation of high-speed water entry cavity of cylinders[J]. Journal of Harbin Institute of Technology, 2014, 46(11): 24-29. DOI: 10.3969/j.issn.1003-1251.2007.06.014.2014.11.004 |
| [10] |
赵成功, 王聪, 魏英杰, 等. 质心位置对超空泡射弹尾拍运动影响分析[J].
北京航空航天大学学报, 2014, 40(12): 1754-1760.
ZHAO Chenggong, WANG Cong, WEI Yingjie, et al. Analysis of the effect of mass center position on tailslap of supercavitation projectile[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(12): 1754-1760. DOI: 10.13700/j.bh.1001-5965.2014.0014 |
| [11] |
王伯秋, 王聪, 魏英杰, 等. 超空泡射弹阻力系数数值模拟[J].
哈尔滨工业大学学报, 2013, 45(3): 22-27.
WANG Baiqiu, WANG Cong, WEI Yingjie, et al. Drag coefficients of supercavitation projectile based on dynamic mesh[J]. Journal of Harbin Institute of Technology, 2013, 45(3): 22-27. DOI: 10.11918/j.issn.0367-6234.2013.03.004 |
| [12] | JOSEPH L, KAYE J. Investigations of water entry phenomena: preliminary studies of effect of atmospheric pressure on trajectory of 2-inch correlation model of Mark 13-6 torpedo[R]. Pasadena, Calif., California Institute of Technology, March 1, 1948. (Hydrodynamics Laboratory Report No. M-59). |
| [13] | TRUSCOTT T T, EPPS B P, BELDEN J. Water entry of projectiles[J]. Annual Review of Fluid Mechanics, 2014, 46(1): 355-378. DOI: 10.1146/annurev-fluid-011212-140753 |
| [14] |
曹伟, 魏英杰, 韩万金, 等. 自然超空泡航行体弹道稳定性分析[J].
哈尔滨工业大学学报, 2012, 44(1): 26-30.
CAO Wei, WEI Yingjie, HAN Wanjin, et al. Simulation of the trajectory stability of natural supercavitation vehicles[J]. Journal of Harbin Institute of Technology, 2012, 44(1): 26-30. DOI: 10.11918/j.issn.0367-6234.2012.01.006 |
| [15] | MAY A. Water entry and the cavity running behavior of missiles[R]. Maryland: NTIS, 1975. |
 2017, Vol. 49
2017, Vol. 49


