船舶耐波性的准确预报是船舶设计的关键要素之一.船舶在波浪中航行时,其产生的垂荡和纵摇运动响应会明显增加船舶阻力;船舶的大幅运动会造成螺旋桨出水,推进效率降低;同时还会影响船上设备的正常运行,严重时导致设备的损坏,甚至船舶会因此短暂或彻底失去控制,发生倾覆.关于船舶耐波性的研究,可分为物理模型试验和数值模拟研究.物理模型试验最大的优点是可靠性高,但其具有成本高、周期长、难以进行系统性研究等缺点.此外,对于甲板上浪、砰击、水花飞溅等强非线性现象,实验条件和测量精度仍不成熟.因此目前关于强非线性船舶运动响应物理模型试验的报道仍较为罕见;数值模拟具有经济性、快捷性、灵活性等优点,传统的船舶耐波性计算方法有切片理论法[1-2],EUT (enhanced unified theory) 法[3],Rankine源法[4-10]等.这些计算工具大都是基于势流理论求解的,忽略了流体的粘性作用,无法考虑船体大幅运动、波浪破碎、水花飞溅、甲板上浪等强非线性现象,而这些强非线性效应对船舶的运动响应有着显著的影响.相对于势流方法,基于粘性流理论的CFD (computational fluid dynamics),可充分考虑船舶航行过程中的粘性效应和强非线性效应.近年来,得到了国内外广大学者的关注,并取得了若干研究成果.如:沈志荣等[11]基于开源代码OpenFOAM开发的数值模型计算分析了Wigley Ⅲ船模在迎浪中的运动响应.石博文等[12]基于粘性流理论建立了三维数值水池,分析了DTMB5512船模在不规则波浪中顶浪航行时的垂荡与纵摇运动时间历程曲线.
CIP (constrained interpolation profile) 方法由Takewaki等[13]于1985年首先提出;Yabe等[14-15]将该方法推广到物理学、电磁学和激光学等学科.Hu等[16]于2004年首次将CIP方法应用到船舶与海洋工程领域,用来计算极端非线性自由液面的流动.随后,He等[17-20]将其应用到处理溃坝问题、波浪与建筑物相互作用、船体耐波性等海洋工程和船舶工程中的强非线性问题.CIP法利用三次多项式进行插值,并同时对物理量和其空间导数进行求解,保证了数值求解在时间、空间上的三阶精度.其具有精度高、稳定性好、数值耗散小等优点.本文采用自编程方式,基于CIP法建立了船舶耐波性强非线性分析模型;并基于该数值模型对波浪中航行的S175船模的运动响应展开了研究,分析了不同入射波高和不同入射波长对S175船模的垂荡和纵摇运动的影响,计算结果与其他数值方法进行了对比验证.最后,计算了S175船模在大浪中的大幅度运动响应,结果表明,该计算模型能较好地模拟船体大幅运动、甲板上浪、底部砰击、水花飞溅等强非线性现象.
1 理论与数值模型本研究采用自编程技术,基于CIP方法建立船舶耐波性分析的粘性流数值模型.文献[17]采用CIP数值模型对Wigley船的强制垂荡运动和纵摇运动进行了线性研究,计算结果与实验值吻合较好.限于篇幅,本文不再详细、全面地叙述该CIP模型的基础理论和数值技术;关于该部分,二维模型具体可参考文献[16, 20],三维模型可参考文献[17].
1.1 控制方程模型以连续性方程、N-S方程为基本控制方程.不考虑温度变化,假设流体是不可压缩的,可以得到以下方程:
| $ \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0, $ | (1) |
| $ \frac{{\partial {u_i}}}{{\partial t}} + {u_j}\frac{{\partial {u_i}}}{{\partial {x_j}}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial {x_i}}} + \frac{1}{\rho }\frac{\partial }{{\partial {x_i}}}\left( {\mu {S_{ij}}} \right) + {f_i}. $ | (2) |
式中:ρ为密度;ui(i=1, 2, 3) 为速度;μ为粘性系数; Sij=∂ui/∂xj+∂uj/∂xi;fi为质量力,如:重力等.其中式 (2) 可用分裂法,将其可分成:
| $ 对流项\;\;\;\;\;\;\;\frac{{u_i^ * - u_i^n}}{{\Delta t}} + u_j^n\frac{{\partial u_i^n}}{{\partial {x_j}}} = 0, $ | (3) |
| $ 非对流项(Ⅰ)\;\;\;\;\;\;\;\frac{{u_i^{ * * } - u_i^ * }}{{\Delta t}} = \frac{1}{\rho }\frac{\partial }{{\partial {x_j}}}\left( {\mu S_{ij}^ * } \right) + {f_i}, $ | (4) |
| $ 非对流项(Ⅱ)\;\;\;\;\;\;\;\frac{{u_i^{n + 1} - u_i^{ * * }}}{{\Delta t}} = - \frac{1}{\rho }\frac{{\partial {p^{n + 1}}}}{{\partial {x_i}}}. $ | (5) |
对流项,式 (3) 采用CIP法计算;扩散项,式 (4) 采用中心差分法;压力-速度耦合项,式 (5) 通过引入连续性方程,可得以下泊松方程:
| $ \frac{\partial }{{\partial {x_i}}}\left( {\frac{1}{\rho }\frac{{\partial {p^{n + 1}}}}{{\partial {x_i}}}} \right) = \frac{1}{{\Delta t}}\frac{{\partial u_i^{ * * }}}{{\partial {x_i}}}, $ | (6) |
式 (6) 为压力泊松方程,同时适用于固体、液体、气体, 可采用SOR (超松弛迭代法) 来迭代求解.
1.2 CIP法CIP法由文献[13]首先提出;文献[16]将其用于船舶与海洋工程领域的强非线性问题的求解.随后文献[17-20]将其在海洋工程和船舶工程中进一步推广.
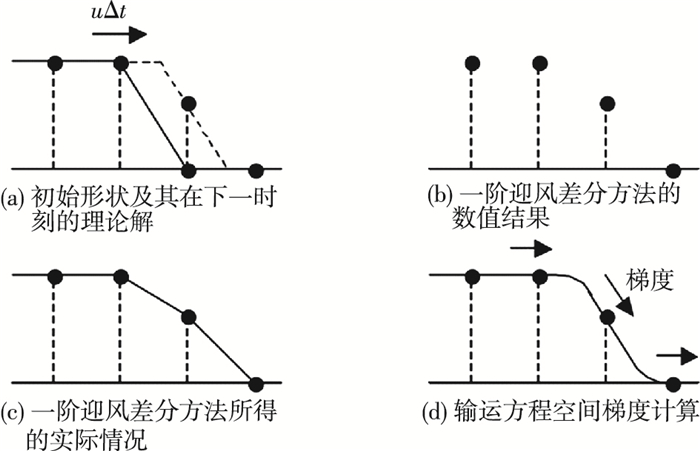
图 1给出了一维CIP方法的原理图.为降低数值耗散,CIP法通过补偿网格间的内部信息来提高数值精度,基本思想为:对于对流项变量f,不仅要计算输运方程的值,而且要计算输运方程的空间梯度 (图 1(d)),即gi=∂f/∂xi,其中f可为ρ、ui和p.f的输运方程可以写成:
|
图 1 一维CIP法原理示意 Figure 1 The principle of CIP method |
| $ \frac{{\partial f}}{{\partial t}} + {u_i}\frac{{\partial f}}{{\partial {x_i}}}H. $ | (7) |
将式 (7) 对空间坐标进行离散,可以得到gi的输运方程:
| $ \frac{{\partial {g_i}}}{{\partial t}} + {u_j}\frac{{\partial {g_i}}}{{\partial {x_j}}} = \frac{{\partial H}}{{\partial {x_i}}} - {g_j}\frac{{\partial {u_j}}}{{\partial {x_i}}}, $ | (8) |
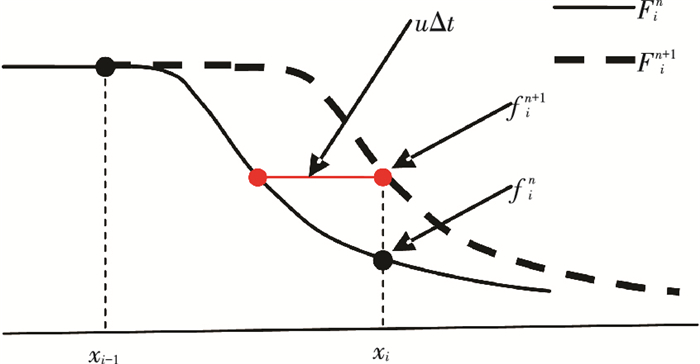
式 (8) 的计算可以分为对流项和非对流项两步,对于式 (7) 和式 (8) 的对流项计算,可以用以下半拉格朗日方法求得 (如图 2所示):
|
图 2 CIP法的半拉格朗日时间步进法 Figure 2 CIP scheme as a kind of Semi-Lagrangian method |
| $ \begin{array}{l} {f^{n + 1}}\left( x \right) = {F^n}\left( {x - u\Delta t} \right), \\ {g^{n + 1}}\left( x \right) = g_i^n\left( {x - u\Delta t} \right). \end{array} $ |
图 2中,Fin和Fin+1分别表示n和n+1时刻的轮廓.其中,插值函数Fn(x) 可以用一个三次多项式来构造,即
| $ F_i^n\left( x \right) = {a_i}{\left( {x - {x_i}} \right)^3} + {b_i}{\left( {x - {x_i}} \right)^2} + {c_i}\left( {x - {x_i}} \right) + {d_i}, $ |
式中,多项式的系数ai,bi,ci,di,可通过强加在xi-1和xi两个网格点处的物理量fn的值以及其梯度值gn共4个量来确定.
1.3 界面捕捉技术为实现自由面的精确重构,本数值模型选择高精度THINC法[21]来重构自由面.其基本思路是将流体的密度函数近似为双曲正切函数,然后通过半拉格朗日法积分得到流量,详细论述请参考文献[21].流体的密度函数的插值函数如下:
1) 当ui+1/2≥0时,
| $ {F_i}\left( x \right) = \frac{\alpha }{2}\left\{ {1 + \gamma \tanh \left[{\beta \left( {\frac{{x-{x_{i-1/2}}}}{{\Delta {x_i}}}-\delta } \right)} \right]} \right\}; $ |
2) 当ui+1/2≤0时,
| $ {F_{i + 1}}\left( x \right) = \frac{\alpha }{2}\left\{ {1 + \gamma \tanh \left[{\beta \left( {\frac{{x-{x_{i + 1/2}}}}{{\Delta {x_{i + 1}}}}-\delta } \right)} \right]} \right\}. $ |
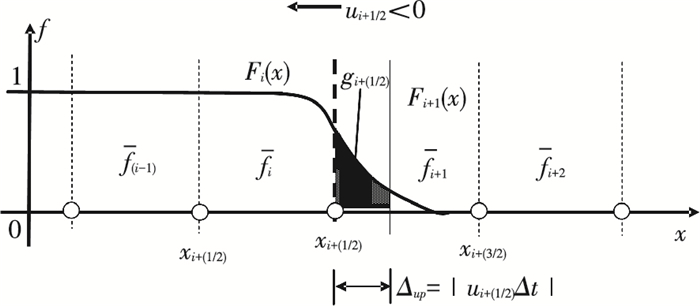
式中:F(x) 为插值函数;u为流速;g为流量;未知参数α、β、γ、δ可通过等量关系和经验公式得到.图 3给出了THINC法的示意图 (ui+1/2≤0).
|
图 3 THINC法插值函数示意 Figure 3 Concept of THINC method |
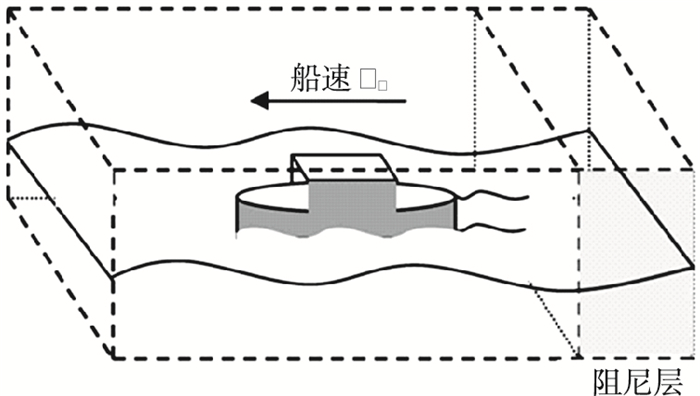
在计算波浪中船舶的运动响应时,船体一般可看作6自由度运动的刚体,且需要定义两个坐标系统:一个是大地坐标系,另一个是随体坐标系.本模型中采用的计算域随着船体航速移动,船体的运动响应也在该随体坐标系下求解.该坐标系采用右手笛卡尔坐标,如图 4所示.原点置于在船中与静水面的交点,x-方向以船尾指向船首为正,z-方向以竖直向上为正.
|
图 4 计算模型 Figure 4 Numerical model |
本文采用ITTC-2010[22](international towing tank conference) 算例对比中的标准船型——S175.S175是一艘长为175 m的集装箱船,其具体主尺度参数见表 1, 船体表面的重构采用虚拟粒子法,其网格 (粒子) 模型如图 5所示.计算域为方形,如图 6所示.计算域的大小x、y、z方向分别设置为:-2.7 L~5.9 L, -1.1 L~1.1 L, -0.8 L~1.3 L;其中L为船长,已在表 1中列出.采用非均匀网格,如:在x、y、z方向的网格数分别为221×81×81.为提高计算精度,在靠近船首附近采用精细网格,最小的网格尺度达Δx=0.010 L;在靠近船体和自由水面处也采用较精细网格,最小的网格尺度为Δy=Δz=0.005 L.
| 表 1 S175集装箱船的主尺度参数 Table 1 Principal dimensions of the S175 container ship |

|
图 5 船体模型 (粒子法) Figure 5 Ship model (Virtual Particle Method) |

|
图 6 计算域与网络划分 Figure 6 Computational domain and grids |
通过模拟S175船模的强制垂荡运动,对建立的数值模型展开了收敛性研究.计算域大小x、y、z方向分别设置为:-2.7 L~5.9 L, -1.1 L~1.1 L, -0.8 L~1.3 L.为保证数值计算的稳定性, 船舶从静止状态逐渐加速到设定航速U.鉴于篇幅,收敛性研究只展示了对数值模拟影响较大的关键参数的计算结果, 如:网格数量和时间步.
船舶强制垂荡运动可以表示为
| $ {\xi _j} = {\alpha _j}\cos {\omega _e}t, \left( {j = 3} \right). $ |
式中:j = 3表示垂荡运动模态;α为垂荡幅值; ωe为垂荡运动圆频率.将纵荡力Fx和垂荡力Fz以ρ▽αωe进行无因次化, 其中,ρ为流体密度, ▽为排水体积; 时间的无因次化因子为Te= 2π/ωe (Te为船舶在波浪中的遭遇周期或强制运动周期). 图 7~8为S175船模在航速Fn = 0.2处以频率为kL=14、振幅为kα=0.28进行强制垂荡运动的数值模拟结果.
|
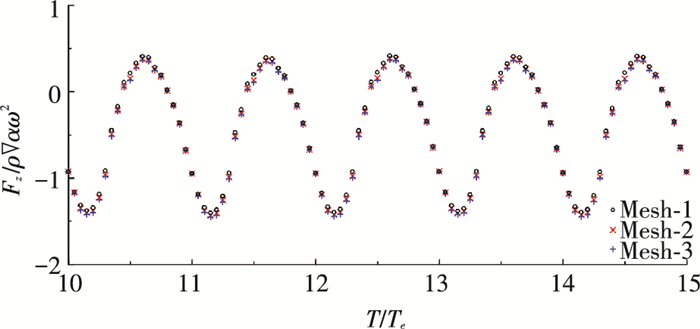
图 7 计算网格对垂荡力的影响 (Fn =0.2, kL=14, kα=0.28) Figure 7 Sensitivity of hydrodynamic force to domain grids for the S175 model |
|
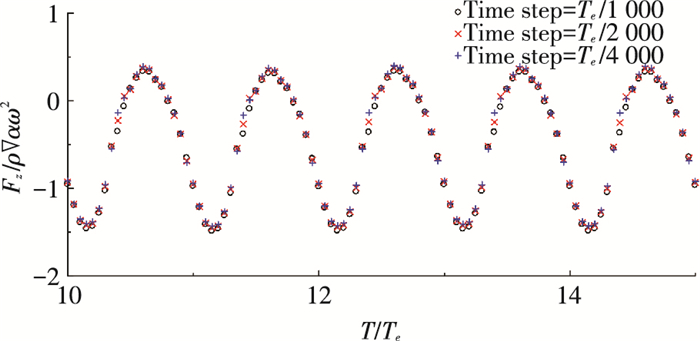
图 8 时间步长对垂荡力的影响 (Fn =0.2, kL=14, kα=0.28) Figure 8 Sensitivity of hydrodynamic force to time step for the S175 model |
图 7给出了3种网格下无因次化垂荡力的计算结果.3种网格数量分别约为Mesh-1 (121×81×81)、Mesh-2 (181×81×81) 和Mesh-3 (221×81×81).相比于Mesh-1,Mesh-2与Mesh-3的计算结果更加接近, 为保证计算精度,以下的数值模拟采用Mesh-3 (221×81×81).
图 8给出了3种不同时间步长对无因次化垂荡力的影响,时间步长分别取为Te/1 000, Te/2 000和Te/4 000, 计算结果并没有较大差异, Te/2 000更接近于Te/4 000.综合考虑计算的时间和精度, 在以下算例中时间步长采用Te/2 000.
2.3 波浪中航行船舶的运动响应经过收敛性研究, 以下数值模拟均采用Mesh-3网格和Te/2 000的时间步长.本文对S175船模在波浪中以航速Fn=0.2迎浪航行的工况展开了系统的研究,分析了不同入射波幅和不同入射波长对船舶运动响应的影响.鉴于目前关于强非线性船舶运动响应物理模型试验仍较为罕见,ITTC于2010年以S175为标准船模进行了多家数值模型计算结果的综合比对,供后继程序的验证与校验之用.在本文中每个波况均计算了12个运动周期Te, 选取稳定后的最后2个周期的垂荡和纵摇运动响应时间历程线,与ITTC-2010 [22]中的两种数值模型的结果展开了对比.计算采用主频为3.40 GHz的Intel I3-3240 CPU, 单核计算占用内存为680 M, 以Te/2 000的时间步长计算12个运动周期Te所需计算时间约为11 h (随输出数据类型及数据量的大小有所变化,如:Tecplot流场数据等).
在图 9~11中, 带实心方点的曲线为本数值模型的计算结果, 三角点为NMRI (national maritime research institute) 的数值模拟结果; ‘×’为NTUA (national technical university of athens) 的数值模拟结果. NMRI所开发的数值模型是基于弱非线性理论,采用二维边界元方法 (2D-BEM) 进行求解.而NTUA开发的数值模型是基于三维边界元方法,可以考虑线性和弱非线性问题.图 9~11给出了S175船在入射波为λ/L=1.0中,以Fn =0.2航行时的垂荡和纵摇运动的响应时间历程线; 图 9~11(a) 和 (b) 分别为无因次化的垂荡运动和纵摇运动的计算结果, kA为无因次化入射波波幅.

|
图 9 船体的垂荡和纵摇运动 (Fn =0.2, λ/L=1.0, kA=0.04) Figure 9 Motions of the S175 hull at kA=0.04 |
|
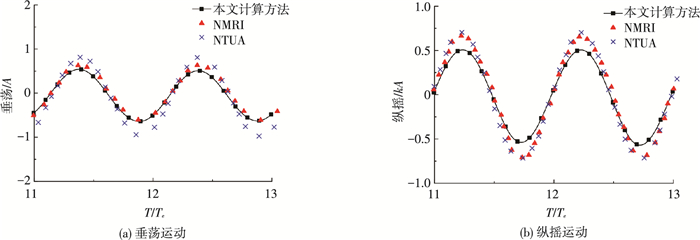
图 10 船体的垂荡和纵摇运动 (Fn=0.2, λ/L=1.0, kA=0.08) Figure 10 Motions of the S175 hull at kA=0.08 |
|
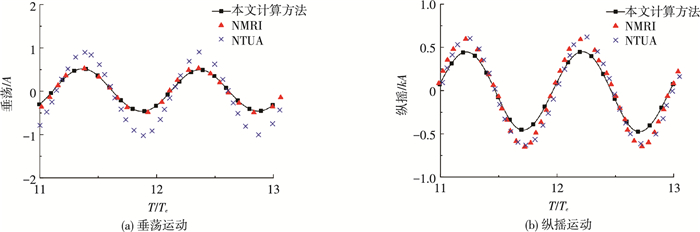
图 11 船体的垂荡和纵摇运动 (Fn=0.2, λ/L=1.0, kA=0.12) Figure 11 Motions of the S175 hull at kA=0.12 |
从图 9~11可以看出:1) 3种数值方法计算的垂荡和纵摇运动响应结果总体吻合较好.2) 从图 9(a)~11(a)可以看出:入射波幅对船体垂荡运动的影响.当入射波幅较小时 (kA=0.04, 图 9(a) ),船体运动的非线性现象不是太明显,仍可以按线性理论进行考虑; NTUA的线性结果与NMRI的结果吻合较好.随着入射波幅增加到kA=0.08和kA=0.12,船体运动和自由面变形的非线性现象更加突出,此时必须采用弱非线性或强非线性理论才能更好地反映和模拟真实的结果.从图 10(a)和图 11(a)可以看出:在kA=0.08和kA=0.12时,本文的强非线性模型的计算结果与非线性理论的NMRI的结果更趋于一致.而NTUA的结果与其他两非线性理论 (NMRI和本数值方法) 的计算结果相差偏大.3) 无论是垂荡还是纵摇运动,总的来说:本计算方法所得的运动响应幅值要略小于其他两种数值方法.其原因为,即使在kA=0.04时,本模型的计算结果也能看到波浪破碎等非线性现象,因此能量也会因为波浪破碎等而有所减小,从而造成船体运动幅值的减小.而基于边界元方法 (NMRI和NTUA) 是无法模拟波浪破碎等强非线性现象,也不存在因为强非线性因素造成的能量损失.因此船舶运动响应的计算结果会较实际值偏大.
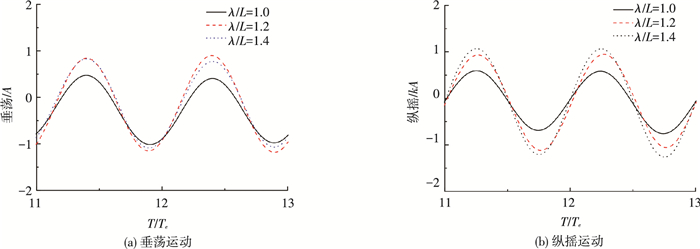
图 12给出了S175船模在不同入射波长下,以航速Fn=0.2航行时的运动响应时间历程线.众所周知,当船体运动的固有周期 (如:纵摇、横摇等周期) 与波浪周期产生共振时,船体将会激起较大的运动幅值.不同的运动模态 (如:垂荡、纵摇、横摇),其各自的固有周期是不同的.从图 12可以看出:随着入射波长的增长,船体垂荡运动在λ/L=1.2时产生较大的运动响应振幅,而纵摇运动则在λ/L=1.4产生较大的运动响应.
|
图 12 3种不同入射波长下,船体的垂荡和纵摇运动 (Fn=0.2, kA=0.04) Figure 12 Motions of the S175 hull at different wave lengths |
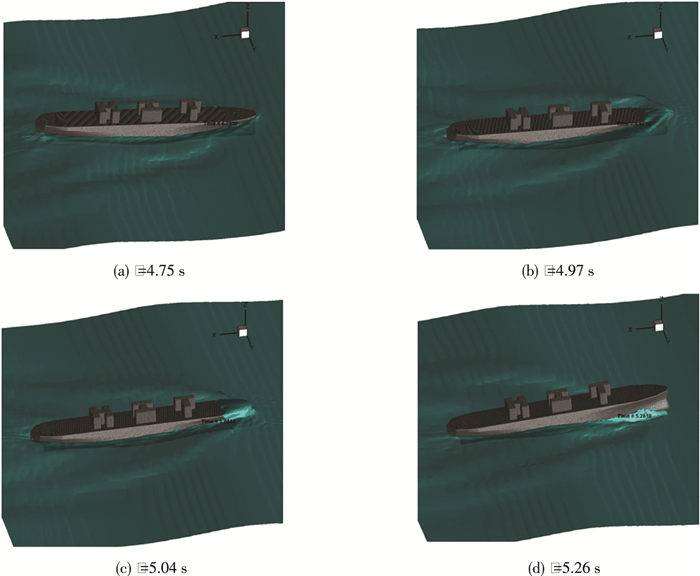
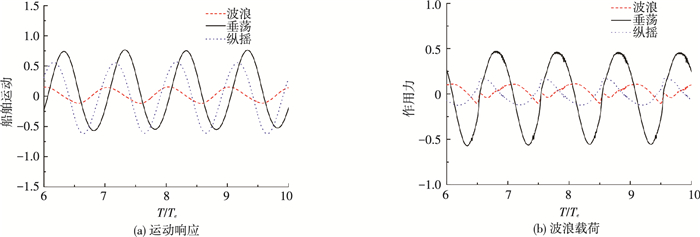
图 13给出了S175船在λ/L=1.2,kA=0.16的波浪中,以航速Fn=0.2迎浪航行时的4个不同时间的运动截图.图 14给出了无因次化的船体运动及其所受波浪载荷随时间的变化历程;其无因次化形式与上述结果一致,即:纵荡运动为Surge/A, 垂荡运动Heave/A, 纵摇运动Pitch/A;纵荡力为Fx/ρ▽Aωe2, 垂荡力Fz/ρ▽Aωe2, 纵摇力矩My/ρ▽ALωe2. 图 13(a)为船体处于接近平衡位置;图 13(b)为船首正俯冲下水,激起较大浪花,船首部受到较大的冲击载荷;图 13(c) 为船体发生甲板上浪,甲板受到上浪拍击的时刻;图 13(d)为船首出水后继续前行,水花飞溅和波浪破碎在船首附近发生.从图 13(b)~图 13(d)可以看出, 该船体运动过程是一个伴随着艏部冲击、甲板上浪和水花飞溅等复杂现象的强非线性过程.因此,相应的船体运动响应和所受的波浪载荷也将是一个强非线性过程,这一点可以从图 14中较易看出,尤其是图 14(b)中,由于冲击载荷的存在,波浪力曲线的局部呈现为锯齿形.
|
图 13 船舶强非线性运动一个周期内的4个不同时刻的快照 (Fn =0.2, λ/L=1.2, kA=0.16) Figure 13 Snapshots of the ship nonlinear motions over a time period |
|
图 14 船舶强非线性运动响应和船舶所受波浪力的时间历程线 (Fn=0.2, λ/L=1.2, kA=0.16) Figure 14 Time history of ship motions and hydrodynamic forces |
1) 本文建立的波浪中航行船舶的强非线性运动响应的数值模型,具有较好的收敛性和精确性.
2) 本模型给出的船模垂荡和纵摇运动响应,与其他数值计算结果吻合较好;由于本模型考虑了粘性和强非线性效应,随着非线性现象的增强,本模型的垂荡运动计算结果与非线性理论的NMRI的结果更趋于一致.
3) 对S175船在大幅波浪中航行时的强非线性运动响应和自由液面大变形 (或破波) 的成功模拟,表明本模型具有较好地模拟水花飞溅、甲板上浪、底部砰击等强非线性问题.
| [1] | 戴仰山, 沈进威, 宋竞正. 船舶波浪载荷[M]. 北京: 国防工业出版社, 2007. |
| [2] |
陈良伟, 肖桃云. 舰船波浪中非线性运动响应与砰击研究[J].
船海工程, 2011, 40(6): 31-34.
CHEN Liangwei, XIAO Taoyun. Study on nonlinear motion response and slam of ship in waves[J]. Ship & Ocean Engineering, 2011, 40(6): 31-34. DOI: 10.3963/J.ISSN.1671-7953.2011.06.009 |
| [3] | KASHIWAGI M. Prediction of surge and its effect on added resistance by means of the enhanced unified theory[J]. Transactions of the West-Japan Society of Naval Architects, 1995, 89: 77-89. |
| [4] | HE Guanghua, KASHIWAGI M. A time-domain higher-order boundary element method for 3D forward-speed radiation and diffraction problems[J]. Journal of Marine Science and Technology, 2014, 19(2): 228-244. DOI: 10.1007/s00773-013-0242-1 |
| [5] |
陈京普, 朱德祥. 船舶在波浪中运动的非线性时域数值模拟[J].
水动力学研究与进展 (A辑), 2010, 25(6): 830-836.
CHEN Jingpu, ZHU Dexiang. Numerical simulations of nonlinear ship motions in waves by a Rankine panel method[J]. Journal of Hydrodynamics, 2010, 25(6): 830-836. DOI: 10.3969/j.issn.1000-4874.2010.06.015 |
| [6] | LIN W M, YUE D K P. Numerical solution for large amplitude ship motions in the time domain [C]// Proceedings of 18th Symposium on Naval Hydrodynamics. Washington DC: National Academy Press, 1991: 41-66. |
| [7] | NAKOS D, SCLAVOUNOS P. Ship motions by a three-dimensional Rankine panel method [C]// Proceedings of 18th Symposium on Naval Hydrodynamics. Washington DC: National Academy Press, 1991: 21-39. |
| [8] | KRING D, SCLAVOUNOS P. Numerical stability analysis for time-domain ship motion simulations[J]. Journal of Ship Research, 1995, 39(4): 313-320. |
| [9] | HUANG Yifeng. Nonlinear ship motions by a Rankine panel method [D]. Massachusetts: Massachusetts Institute of Technology, 1997. |
| [10] | KIM Y, KIM K H, KIM J H, et al. Time domain analysis of nonlinear motion responses and structural loads on ships and offshore structures: development of wish programs[J]. International Journal of Naval Architecture and Ocean Engineering, 2011, 3(1): 37-52. DOI: 10.2478/IJNAOE-2013-0044 |
| [11] |
沈志荣, 叶海轩, 万德成. 船舶在迎浪中运动响应和波浪增阻的RANS数值模拟[J].
水动力学研究与进展 (A辑), 2012, 27(6): 621-633.
SHEN Zhirong, YE Haixuan, WAN Decheng. Motion response and added resistance of ship in head waves based on RANS simulations[J]. Journal of Hydrodynamics, 2012, 27(6): 621-633. DOI: 10.3969/j.issn1000-4874.2012.06.001 |
| [12] |
石博文, 刘正江, 吴明. 船模不规则波中顶浪运动数值模拟研究[J].
船舶力学, 2014, 18(8): 906-915.
SHI Bowen, LIU Zhengjiang, WU Ming. Numerical simulation of ship motions in irregular head waves[J]. Journal of Ship Mechanics, 2014, 18(8): 906-915. DOI: 10.3969/j.issn.1007-7294.2014.08.005 |
| [13] | TAKEWAKI H, NISHIGUTI A, YABE T. Cubic interpolated pseudo-particle method (CIP) for solving hyperbolic-type equations[J]. Journal of Computational Physics, 1985, 61(2): 261-268. DOI: 10.1016/0021-9991(85)90085-3 |
| [14] | YABE T, AOKI T. A universal solver for hyperbolic equations by cubic-polynomial interpolation Ⅰ. One-dimensional solve[J]. Computer Physics Communications, 1991, 66(2/3): 219-232. DOI: 10.1016/0010-4655(91)90071-R |
| [15] | YABE T, ISHIKAWA T, WANG Peiyuan, et al. A universal solver for hyperbolic equations by cubic polynomial interpolation Ⅱ. Two-and three-dimensional solvers[J]. Computer Physics Communications, 1991, 66(2/3): 233-242. DOI: 10.1016/0010-4655(91)90072-S |
| [16] | HU Changhong, KASHIWAGI M. A CIP-based method for numerical simulations of violent free-surface flows[J]. Journal of Marine Science and Technology, 2004, 9(4): 143-157. DOI: 10.1007/s00773-004-0180-z |
| [17] | HE Guanghua, ISSHIKI T, KASHIWAGI M, et al. Prediction of Radiation Forces by Means of a CIP-based Cartesian Grid Method [C]// Proceedings of 21st International Offshore and Polar Engineering Conference. Maui, Hawaii: International Society of Offshore and Polar Engineers, 2011, 2: 633-638. |
| [18] | ZHAO Xizeng, HU Changhong. Numerical and experimental study on a 2-D floating body under extreme wave conditions[J]. Applied Ocean Research, 2012, 35: 1-13. DOI: 10.1016/j.apor.2012.01.001 |
| [19] | LIAO Kangping, HU Changhong. A coupled FDMFEM method for free surface flow interaction with thin elastic plate[J]. Journal of Marine Science and Technology, 2013, 18(1): 1-11. DOI: 10.1007/s00773-012-0191-0 |
| [20] | HE Guanghua. A new adaptive Cartesian-grid CIP method for computation of violent free-surface flows[J]. Applied Ocean Research, 2013, 43: 234-243. DOI: 10.1016/j.apor.2013.10.004 |
| [21] | XIAO Feng, HONMA Y, KONO T. A simple algebraic interface capturing scheme using hyperbolic tangent function[J]. International Journal for Numerical Methods in Fluids, 2005, 48(9): 1023-1040. DOI: 10.1002/fld.975 |
| [22] | KIM Y. Comparative study on linear and nonlinear ship motion and loads [C]// Proceedings of ITTC Workshop on Seakeeping. Seoul: Seoul National University, 2010: 283-310. |
 2017, Vol. 49
2017, Vol. 49


