现代信息化的快速发展使水下无人航行器 (AUV) 扮演着重要的角色.而导管螺旋桨相对传统螺旋桨能够在高负荷时有效地提供额外推力,应用在AUV上具有高效率、大推力、小尺寸、使用灵活、易于控制等优点[1],如美国的“蓝鳍金枪鱼”-21型AUV和中国的“无影”系列AUV上,都采用导管螺旋桨作为推进器.这种航行器一般都是电驱动的[2],如蓝鳍金枪鱼”最高续航力为25 h,而执行一次任务 (包括下潜、侦测、数据下载、上浮) 需要24 h,续航力比较勉强.因而提高导管桨的推进效率对延长续航时间具有十分重要的作用.考虑到AUV通常工作在较深的水下,且航速较低,一般不发生空化,可能影响导管桨性能的参数有很多,包括导管参数如直径比和长径比,螺旋桨的参数如盘面比、螺距比等,因此本文从充分发挥导管螺旋桨高效率推进性能的角度出发,通过对比不同导管长径比、直径比、盘面比与螺距比对效率的影响,对导管螺旋桨的极限效率进行了分析.
目前对于导管螺旋桨性能的模拟主要有传统方法和CFD分析两类.传统方法主要有面元法[3]和升力面涡格法[4],Zhang等[5]将导管和桨叶分别采用面元法和涡格法对JD简易导管可调螺距桨进行了数值研究,螺距比对性能的影响稍有提及.随着计算机技术的发展,Kim[6]通过求解RANS方程获得导管桨叶梢处的压力分布以及桨叶和导管边界层、涡核处湍流的发展,证明了RANS方法能够很好地还原流场信息. Krasilnikov等[7]以该方法研究了导管桨的尺度效应,Streckwall等[8]比较了使用9种不同编码求解黏流的CFD软件诸如Fine/Turbo、ISIS、STARCD、OpenFoam等的求解结果,发现除叶梢处流场有差异,其性能基本吻合.本文将采用商用软件的CFX,首先研究各主要设计参数对导管螺旋桨水动力性能的影响,然后分析多个参数对导管螺旋桨最高效率线的影响规律,进而寻得极限效率.
1 导管螺旋桨设计本文采用基于荷兰实验室的19A/Ka4-50导管螺旋桨,该桨采用19A导管,设计长径比L/D(导管横向最外端两端距离L与桨叶半径D之比) 为0.5,直径比D1/D2(导管外壁直径D1与内壁直径D2之比) 为1.21,初始桨叶的参数见表 1,导管桨的整体外观如图 1所示.
| 表 1 桨叶参数 Table 1 Property parameter of propeller |

|
图 1 19A/Ka4-50导管桨外观 Figure 1 19A/Ka4-50 series ducted propeller model |
将导管的内壁面从0.5倍弦长位置截断,分别向前后移动0.125或0.250倍弦长得到长径比分别为0.6和0.7的加长导管L0.6和L0.7;接着,在保证前后缘导圆的情况下用直线连接导管外壁面,得到新的加长导管. 图 2为初始长径比和加长后的导管剖面形状.

|
图 2 不同长径比导管 Figure 2 Duct with variable length-diameter ratio |
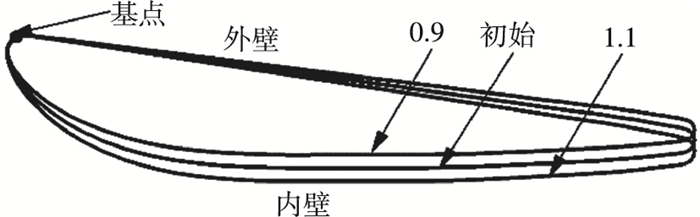
以导管外壁边缘一点为基点,在保证导管外壁直径大小不变的基础上,将导管纵向尺寸按比例扩大或缩小从而得到不同的直径比. 图 3所示即为基于基点等将初始导管沿径向等比例扩大0.9倍和1.1倍后得到的导管外观图.
|
图 3 不同直径比导管 Figure 3 Duct with variable diameter ratio |
螺距比P/D为螺距与螺旋桨直径之比,盘面比AE/Ao为桨叶伸张轮廓面积与圆盘面积之比.
保持各叶切面处翼型不变,保证各切面处翼型螺距角相等,改变不同半径处的翼型的扭角并保证各半径处螺距角相等得到不同螺距比的桨叶;将各半径处翼型弦长等比例增大或缩小得到不同盘面比的桨叶.由于实际工程中螺距比和盘面比的选取范围很大,本文限定螺距比为0.963~2.200,盘面比为0.4~0.6来进行研究.
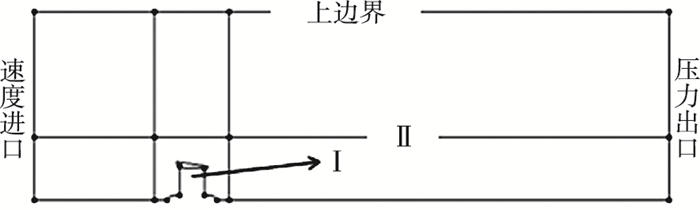
2 数值分析方法与验证如图 4所示,将求解区域划分为旋转域Ⅰ和固定域Ⅱ,为了避免进口和出口区域与半径方向处流场的干扰,固定域Ⅱ中螺旋桨前方、后方、径向处范围分别为10倍、30倍、10倍桨叶直径,使流场充分延伸.在近壁面处,通过对不同Y+值网格模型的计算,如导管、桨穀处网格,控制Y+在10以内,桨叶处Y+控制在1以内,保证壁面处有足够密的附面层网格.
|
图 4 网格区域划分及边界条件 Figure 4 Region for mesh and boundary condition |
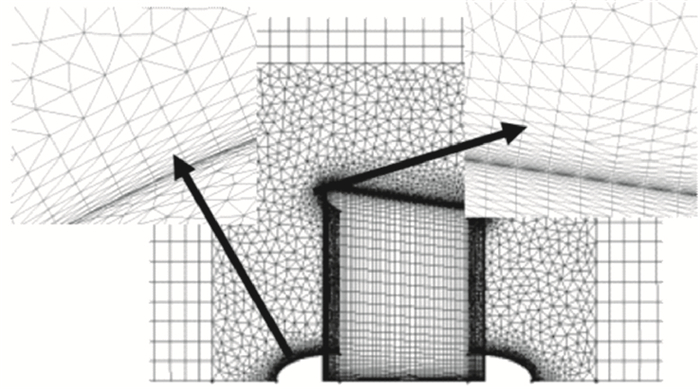
图 5为子午面流场网格及壁面处加密后的效果图.在固定域中包含桨穀处采用非结构化网格,为节省计算量,其他区域中采用结构化网格.
|
图 5 静转交接处子午面网格 Figure 5 Mesh of RS border in meridian plane |
由于桨叶相对导管在旋转,故存在移动网格的处理问题采用多重参考网格 (MFR) 方法[9],在转静交界面上采用通用网格交界面 (GGI) 技术处理.
采用基于雷诺平均的N-S控制方程:
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial {x_i}}} = 0, $ | (1) |
| $ \begin{array}{l} \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}{u_j}} \right)}}{{\partial {x_j}}} = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[{\mu \left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)} \right] + \frac{\partial }{{\partial {x_j}}}\left( { - \rho \overline {{{u'}_i}{{u'}_j}} } \right). \end{array} $ | (2) |
式中:式 (1) 为连续性方程,式 (2) 为动量方程. ui为x方向的绝对速度;p为静压;μ为流体的黏性系数;δij为克罗内克函数;
考虑到k-w方程对近壁区域及尾流还有绕流计算的比较好,以及对结果精确性的要求,本文采用SST k-w湍流模型[10].
导管螺旋桨完全沉入深水中,且不受自由液面的影响,在边界条件设置中出口处相对压力设为0,在分析流场形态时可加上水压头.固定螺旋桨转速N=600 r/min,改变进速VA来模拟在水槽中的实验状态.
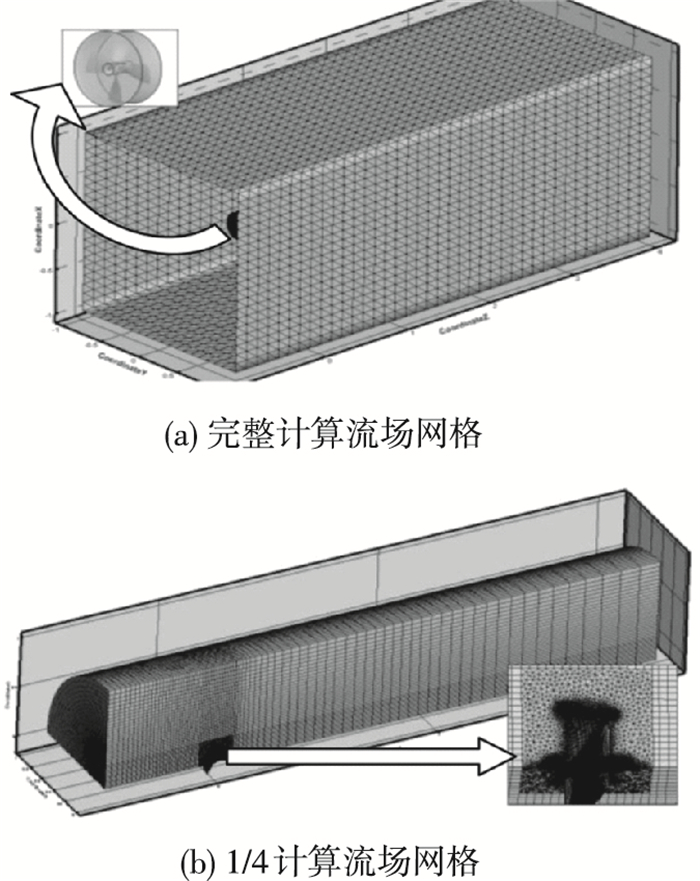
2.1 不同计算域对比由于本文中螺旋桨工作在均匀来流中,4个桨叶通道的流场呈周期性规律,为了节省计算成本,在数值计算过程中计划只模拟1/4的流场,为了验证计算结果的精确性,对完整流场与1/4的流场做对比分析,本文中所取导管内壁与叶梢间隙为2 mm. 图 6(a), (b)分别为完整流场和1/4流场网格模型.
|
图 6 不同类型计算网格 Figure 6 Different numerical mesh types |
如图 7所示为两种网格的性能对比,推力系数KT、扭矩系数KQ、敞水效率η在设计点附近基本吻合,最大误差不超过3%.

|
图 7 不同类型网格性能计算对比 Figure 7 Results of different mesh types |
工程上为防止叶梢压力面处流体绕过间隙与来流形成自由涡而对导管桨性能所造成的影响,尽量减小叶梢的间隙.为此本文研究了间隙大小对性能的影响规律.如表 2所示为导管桨叶梢与内壁间之间间隙为1 mm和2 mm时敞水性能的对比.
| 表 2 不同叶梢与内壁之间间隙性能 Table 2 Results of different clearance between blade tip and shroud |
对比表 2中间隙1 mm (4‰D) 和2 mm (8‰D) 的性能可以发现间隙为1 mm时的效率明显高于间隙为2 mm时的效率,这一点与文献[11-13]中数值计算得到的效率随间隙变化规律一致.相对于2 mm的间隙,1 mm间隙的导管桨高出约2~4个百分点.对于推力系数和扭矩系数随间隙增大而增大的规律,本文的计算结果与文献[12]一致,与文献[11, 13]的结果存在出入.因此间隙对导管桨性能的影响还需要做进一步的实验验证,以作为今后数值计算的参考资料.考虑到工艺、安装、变形等因素,一般叶梢间隙取4‰D以内.因此本文的后续工作将以叶梢间隙1 mm为重点来研究.
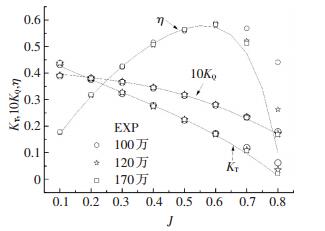
2.3 网格数目对比为选取合适的网格数,本文对多种网格数目的静止域进行了分析,由于导管附近流动黏性较大,所以包围导管的静止域网格密度对捕捉流动细节、性能计算影响较大.保持旋转域的网格数不变,改变静止域网格节点数,从而得到100万、120万、170万固定域网格,其数值结果与实验结果[14]对比如图 8所示.
|
图 8 不同计算域网格导管桨性能数值模拟结果与实验结果对比 Figure 8 Results of different grid number and experimental data |
可以看出推力系数在高进速系数时误差较大,从而导致效率在高进速系数时误差较大.网格数目在120万时误差已经很小,相对170万网格时推力系数误差在0.01%以内.为了能够在精确模拟导管桨性能的同时节省计算量,本文后续工作采用120万固定域网格数目进行数值模拟.
3 不同参数对性能的影响 3.1 导管长径比的影响增大桨叶盘面比或螺距比时在剖面视图中桨叶宽度将增大,为保证桨叶从导边到随边范围内等叶梢间隙,需要加长19A导管,并研究加长后导管的性能.如图 9所示为加长后的导管与原导管性能对比.

|
图 9 不同长径比的导管桨水动力性能 Figure 9 Hydrodynamic performance of different length-diameter ratio |
观察图 9可以发现,与加长后的导管性能对比推力系数和扭矩系数相对误差在设计工况中均在3%以内,最终所得的效率误差在1%以内.考虑到导管内壁与叶梢处之间流场可能会发生变化.因此将继续研究导管在不同长径比时的流场情况.
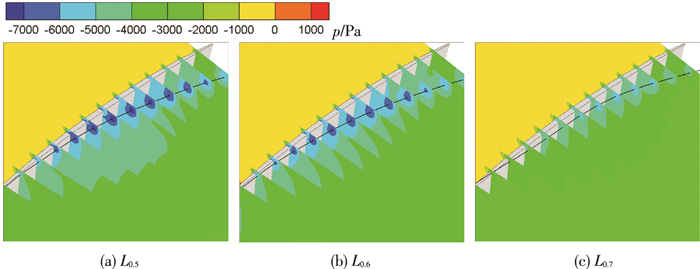
如图 10、11为J=0.4时不同长径比垂直于桨叶表变的涡量云图和压强云图.

|
图 10 不同长径比的涡量云图 Figure 10 Vorticity contours of different length-diameter ratio |
|
图 11 不同长径比的压强云图 Figure 11 Pressure contours of different length-diameter ratio |
图 10、11中,由于桨叶、叶梢和导管内壁表面黏性的作用,故该区域附近域涡量比其他区域都大,在叶梢间隙中,靠近叶梢处的剪切作用比到导管内壁处更明显,这说明间隙处主要是附面层和流动分离占据了主导地位.
随着长径比的增大,最大涡量逐渐减小,最低压力点处压力也逐渐增大,说明越不容易发生空化,并且最低压力点先远离吸力面,后靠近吸力面.从涡量图中可以看出剪切作用同最低压力点发展方向一致,最大涡量与最低压力点近似重合,所以推断最大剪切位置一般发生在最低压力点处[15].
图 10中在叶梢间隙处弦向位置由导边到随边自由泄漏涡 (TLV) 逐渐增强并向上游发展,由TLV引起的空化一般发生在叶梢弦向中间处[16],图 10(b)中在叶梢弦向中间压力最低点处形成了明显的梢涡,并且在间隙处存在分离涡.
3.2 螺距比的影响在导管长径比的影响中已经得知加长后的导管对导管桨性能影响微小,其效率误差均在1%以内,表 3中所示为不同螺距比的桨叶所对应的导管长径比.
| 表 3 不同螺距比对应的导管长径比 Table 3 Different pitch ratio corresponding to variable length-diameter ratio |
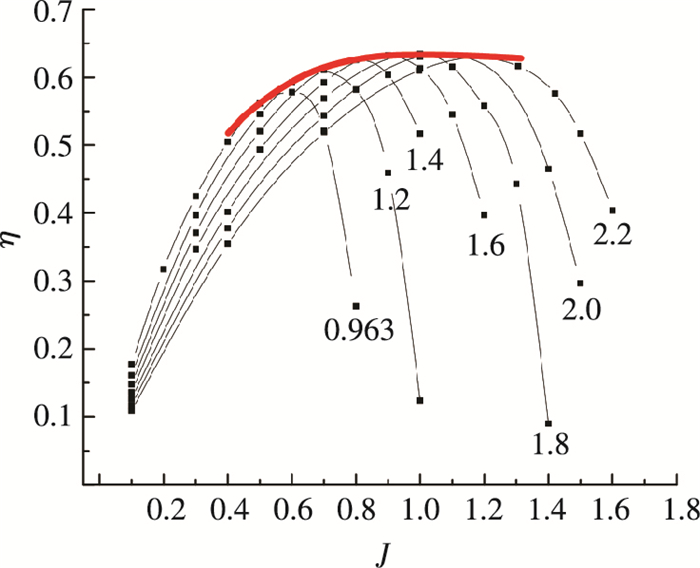
本文重点研究桨叶参数对效率的影响,因此图 12中只显示螺距比对效率的影响.
|
图 12 不同螺距比的导管桨水动力性能 Figure 12 Hydrodynamic performance of different pitch ratio |
螺距比的增大会使叶元体与水流之间攻角增加,从而升力和阻力增加,最终使扭矩系数和推力系数都增大.对于效率,重载时随螺距比的增大而减小,轻载时随螺距比的增大而增大;并且随着螺距比的增大,最高效率也会提高,最高效率点对应的进速系数也提高,其有效进速系数范围增大.
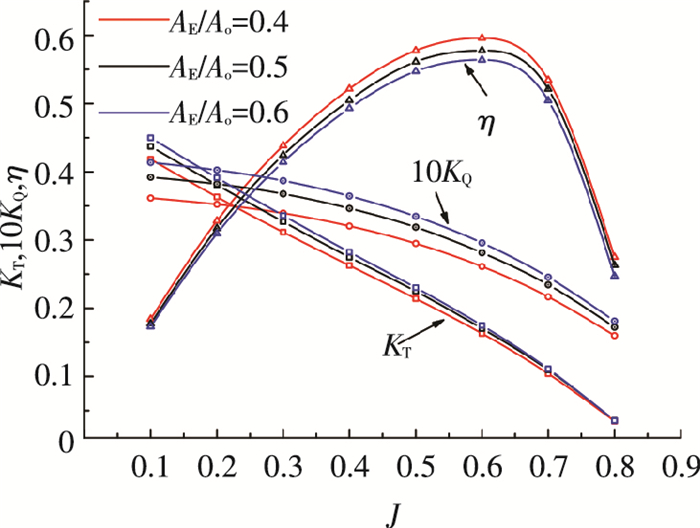
3.3 盘面比的影响桨叶数目固定,即4叶桨,通过增大或减小各半径处弦长改变盘面比.如图 13所示为不同盘面比导管桨的敞水性能对比.
|
图 13 不同盘面比的导管桨水动力性能 Figure 13 Hydrodynamic performance of different blade area-ratio |
从图 13中可以看出桨叶数目固定,盘面比的增加会造成导管桨推力系数、扭矩系数的提高,但是却会导致效率的降低.虽然桨叶面积增大会使升力和阻力增加,从而使推力系数和扭矩系数增大,但是也会造成导管桨内水流的堵塞效应,使得效率降低.
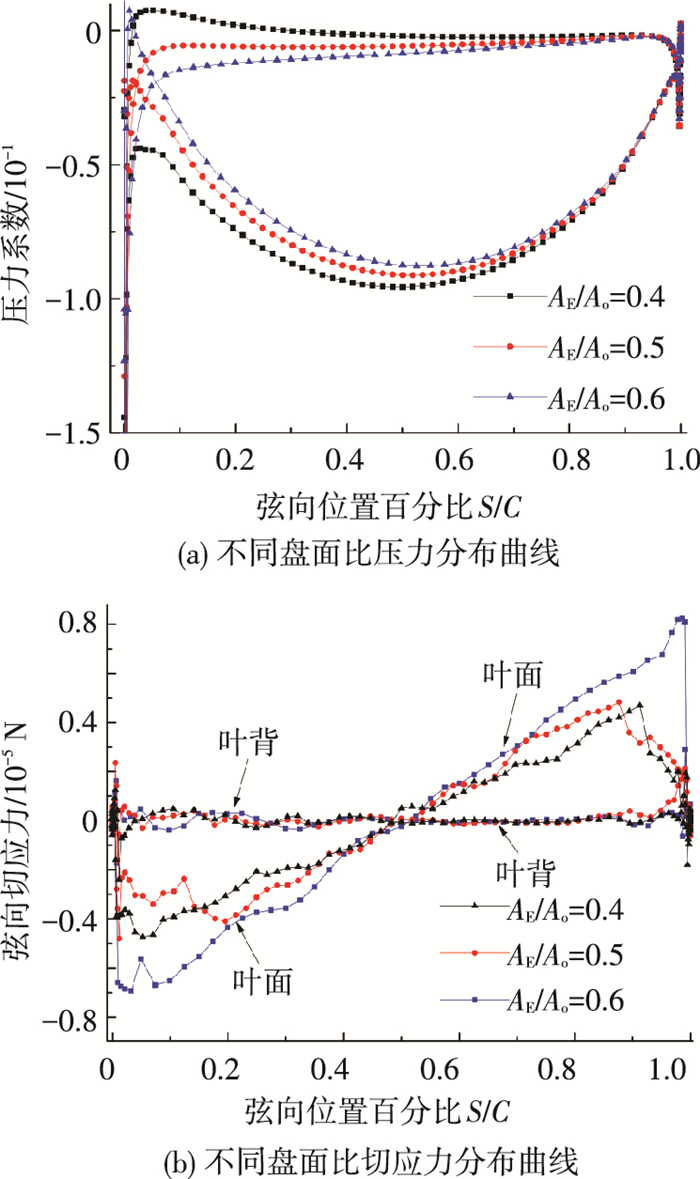
从图 13中还可以看出在J=0.6时效率相差较大,而0.75半径处为决定螺旋桨性能的切面,故以J=0.6,r/D=0.75为条件研究不同盘面比处桨叶的受力情况.如图 14所示为相应条件下的桨叶表面受力情况.
|
图 14 J=0.6时不同盘面比桨叶受力曲线 Figure 14 The force curve of blade of different disc area ratio |
图 14中各个参数意义如下:
| $ {C_p} = p/\left[{\rho {v^2}{{\left( {1 + \frac{{\pi {d_r}}}{J}} \right)}^2}} \right]. $ |
式中:p为相对压力,即桨叶表面压力相对等水深无穷远处的压力;dr为弦长所在半径与桨叶半径比值r/R,本例中取dr=0.75.图中S为展开翼型表面各点至导边的距离,C为翼型弦长.
| $ \tau = \mu \cdot \frac{{{\rm{d}}{V_0}}}{{{\rm{d}}{Z_0}}}. $ |
式中:τ为切应力;V0为平行于弦向位置的切向速度;Z0为垂直于弦向位置的方向;μ为动力黏性系数,取0.000 889 9 (kg/m·s).
从图 14(a)中可以看出,随着盘面比的增加,叶面处压力系数会减小,叶背处则相反.并且距离导边越远,桨叶压力面和吸力面的压力系数随盘面比的变化越小,并在50%弦长以后不同盘面比的压力系数几乎接近.可以看出虽然较小盘面比处压力差较大,但是压力差的增大不及盘面积的减小,从而造成较大的盘面比反而拥有较高的推力系数.从图 14(b)中可以看出,在叶面处,较大盘面比的切应力也较大,在约50%弦长以内和50%弦长以外方向相反,说明水流方向在叶切面处分流.而在叶背切应力几乎不随盘面比而改变,并且接近于0.因此总体来说,盘面比增大会使剪应力增大,再加上桨叶面积的增大,进而使摩擦阻力增大,因此较大的盘面比的导管桨扭矩系数较高.这也是引起导管桨效率降低的因素之一.
3.4 导管直径比的影响导管直径比的改变会造成叶梢间隙的增大或减小,为降低梢涡的影响,叶梢间隙仍取为1 mm,桨叶直径沿初始桨叶形状稍微加长或减小,表 4所示为在初始导管的基础上增加相应倍数并且叶梢间隙不变的情况下桨叶和导管的参数变化.
| 表 4 导管直径比对应桨叶参数 Table 4 Blade parameter corresponding to diameter ratio of duct |
从表 4中可以看出,在初始桨叶半径的基础上适当的增加或减小一部分不仅不会造成盘面比太大的变化 (AE/Ao≈0.5),即可以忽略盘面比造成导管桨性能的变化,而且在实际工程中也有利于桨叶的加工.
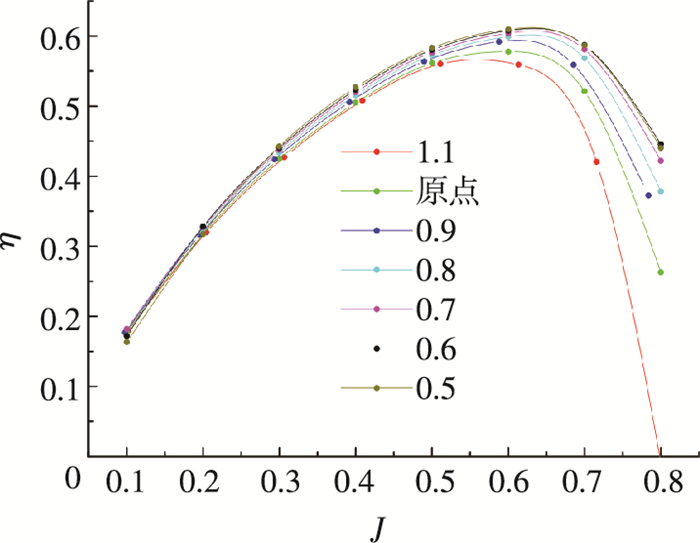
图 15为不同导管直径比下的导管桨效率曲线.可以看出,当导管直径比减小时,导管桨的效率会不断增大并且当直径比减小到一定程度时,其效率达到最大值,不再继续升高.综合考虑,最佳导管取基于基点扩大0.6倍后的直径比,此时导管直径比为1.117.
|
图 15 不同导管直径比的效率曲线 Figure 15 Efficiency curve of different duct diameter ratio |
通过对导管桨多个参数的分析发现,适当改变导管长径对其水动力性能并不存在影响,而螺距比、盘面比、导管直径比对导管桨性能的影响不可忽略.因此将以这3个参数为指标,以效率最高为目标,通过作一系列的包络线寻找最优效率.
假设盘面比、导管直径比一定,螺距比为参数c,则:
| $ F\left( {J, \eta, c} \right) = 0, $ | (3) |
| $ \frac{{\partial F\left( {J, \eta, c} \right)}}{{\partial c}} = 0. $ | (4) |
式中:F指在某一参数c即螺距比时的一条效率曲线,若已知多条参数c下的效率曲线,联立式 (3),(4),消除参数c,即可得到包络线l的表达式.
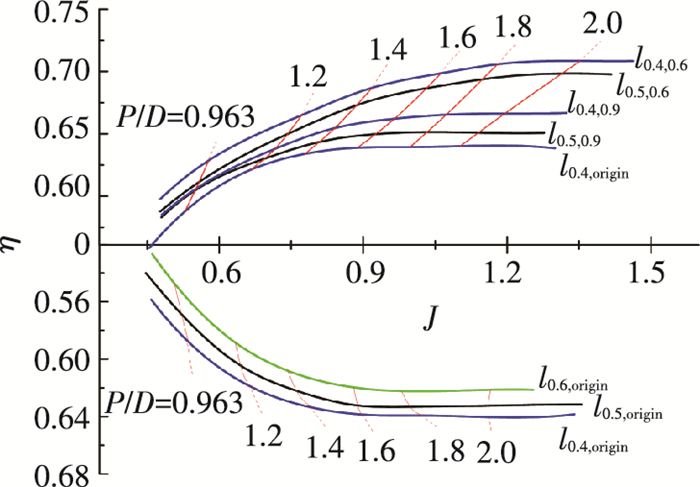
在包络线上的每一个点都有一条与c相关的效率曲线和它在这点相切,这一点为设计点对应的最高效率点.求不同螺距比效率曲线的包络线的基本步骤为:1) 以初始导管桨为算例,即AE/Ao=0.5,D1/D2=1.212,数值模拟得到不同螺距比下的效率曲线簇;2) 通过对同一进速系数J0同螺距比的效率η00、η01、η02、…进行比较,得到最高效率值,以此点为包络线与曲线簇的切点,依次作出J1、J2、J3下的切点,画出包络线l0,图 16红色线所示即为效率曲线簇的包络线;3) 依次作出不同盘面比和直径比下的效率曲线簇,求得各组包络线l0、l1、l2、…;4) 在设计工况已知的情况下,可以通过插值寻求在已知工况时不同参数下的最优效率所对应的桨叶螺距比.如图 16所示即为数值模拟不同参数导管桨时得到效率曲线后处理得到的包络线.其中“l0.5, 0.6”代表AE/Ao=0.5,基于基点等将初始导管沿径向等比例扩大0.6倍后的导管桨在不同螺距比时效率曲线簇的包络线.红色线条为不同包络线上的相同螺距比的连线. 图 16上为不同直径比时的包络线,图 16下为不同盘面比的包络线.
|
图 16 不同盘面比和螺距比对应的包络线 Figure 16 Envelope line of different area ratio and pitch ratio |
为了验证上述求包络线方法的正确性,本文将以图 16中的一条包络线上的点为设计参数.根据图 16可以看出l0.4, 0.6为极限效率对应的包络线,假设以AE/Ao=0.4,D1/D2=1.117为设计参数,以J=0.65和J=0.9为设计工况,通过插值得到螺距比分别为1.06和1.30.选择好相应参数进行数值计算得到如表 5所示的性能.
| 表 5 螺距比为1.06、1.30时的敞水效率 Table 5 Open water efficiency of pitch ratio equal to 1.06 and 1.30 |
如图 17所示为根据表 5,6中数据所得到的螺距比分别为1.06,1.30时的效率曲线图,可以看出P/D=1.06时,效率曲线与包络线相切,而P/D=1.30虽不完全相切,但基本接近于包络线,并且有相切的趋势.说明导管桨以包络线的形式来设计是合理的.

|
图 17 包络线与效率曲线对比 Figure 17 Comparison of envelope line with efficiency curve |
1) 在导管两端曲率不变,合理控制导管长径比的前提下,导管桨的性能与长径比无关.并且随着长径比的增大梢部空泡数逐渐提高.但梢涡涡核位置随长径比的变化规律不确定.增大螺距比会提高导管桨的推力和扭矩,部分工况下效率会提升,最高效率提升,同时有效工况范围增加.在桨叶数目不变的前提下,随着盘面比的增大导管桨的效率会有所降低.叶背的压力随之升高,可提升空化性能.在保持叶梢与导管内壁间隙和导管外径不变的情况下,降低直径比可以提升导管桨的效率,同时最高效率点所对应的进速系数值增大.
2) 通过绘制各个参数下不同螺距比效率曲线簇的包络线,可以在已知设计工况的情况下方便插值得到最高效率所对应的各个参数.
| [1] |
吴光林, 严谨. 船用螺须桨的应用与发展趋势[J].
广东造船, 2008(4): 49-51.
WU Guanglin, YAN Jin. Application and trend in development of marine propeller[J]. Guangdong Shipbuilding, 2008(4): 49-51. |
| [2] |
赵涛, 刘明雍, 周良荣. 自主水下航行器的研究现状与挑战[J].
火力与指挥控制, 2010, 35(6): 1-6.
ZHAO Tao, LIU Mingyong, ZHOU Liangrong. A survey of autonomous underwater vehicle recent advances and future challenges[J]. Fire Control & Command Control, 2010, 35(6): 1-6. DOI: 10.3969/j.issn.1002-0640.2010.06.001 |
| [3] | KERWIN J E, KINNAS S A, LEE J T, et al. A surface panel method for the hydrodynamic analysis of ducted propellers[J]. Society of Naval Architects and Marine Engineers, 1987, 95: 93-122. |
| [4] | KOBAYAKAWA M, ONUMA H. Propeller aerodynamic performance by vortex-lattice method[J]. Journal of Aircraft, 2012, 22(8): 649-654. DOI: 10.2514/3.45181 |
| [5] | ZHANG Jianhua, WANG Guoqiang. Prediction of hydrodynamic performances of ducted controllable pitch propellers[J]. Journal of Ship Mechanics, 2002, 6(6): 18-27. |
| [6] | KIM J. Sub-visual cavitation and acoustic modeling for ducted marine propulsor[D]. Iowa City: The University of Iowa, 2002. |
| [7] | KRASILNIKOV V I, ZHANG Zhirong, HONG Fangwen, et al. Steady analysis of viscous flow around ducted propellers: validation and study on scale effects[C]// Proceeding of the 9th International Conference on Fast Sea Transportation FAST2007. Shanghai, China: [s.n.], 2007. |
| [8] | STRECKWALL H, SALVATORE F. Results of the Wageningen 2007 workshop on propeller open water calculations including cavitation[J]. Proceedings of the RINA CFD, 2008. |
| [9] | LUO J Y, GOSMAN A D. Prediction of impeller-induced flow in mixing vessels using multiple frames of reference[J]. Institute of Chemical Engineers Symposium Series, 1994, 136: 549. |
| [10] |
吕晓军, 周其斗, 纪刚, 等. 导管螺旋桨敞水性能的预报和比较[J].
海军工程大学学报, 2010, 22(1): 24-30.
LV Xiaojun, ZHOU Qidou, JI Gang, et al. Prediction and comparison of open water performance of ducted propeller[J]. Journal of Naval University of Engineering, 2010, 22(1): 24-30. DOI: 10.7495/j.issn.1009-3486.2010.01.006 |
| [11] | NI Haoliang, ZHOU Junwei, WANG Dazheng. Influence of finite tip clearance on the tip flow characteristics of ducted propeller[J]. Advanced Materials Research, 2014, 889-890: 374-379. DOI: 10.4028/www.scientific.net/AMR.889-890.374 |
| [12] |
张文璨, 董国祥, 陈伟民, 等. 叶梢与内壁间隙对导管螺旋桨水动力性能的影响[J].
上海船舶运输科学研究所学报, 2015, 38(4): 8-13.
ZHANG Wencan, DONG Guoxiang, CHEN Weimin, et al. Influence of clearance between the blade tip and the inner wall of duct on hydrodynamic performance of ducted propellers[J]. Journal of Shanghai Ship & Shipping Research Institute, 2015, 38(4): 8-13. DOI: 10.3969/j.issn.1674-5949.2015.04.002 |
| [13] |
李坚波. 叶梢间隙对导管桨性能的影响分析[J].
船海工程, 2010, 39(3): 36-39.
LI Jianbo. CFD analysis of tip clearance effects on duct propeller's performance[J]. Ship & Ocean Engineering, 2010, 39(3): 36-39. DOI: 10.3963/j.issn.1671-7953.2010.003.09 |
| [14] | KUIPER G. The wageningen propeller series[M]. Netherland: MARIN Publication, 1992. |
| [15] |
周军伟, 王大政. 导管螺旋桨不同桨叶的叶梢泄露涡分析[J].
哈尔滨工业大学学报, 2014, 46(7): 14-19.
ZHOU Junwei, WANG Dazheng. Analysis of tip leakage vortex of different blade in ducted propeller[J]. Journal of Harbin Institute of Technology, 2014, 46(7): 14-19. DOI: 10.11918/j.issn.0367-6234.2014.07.003 |
| [16] | NI Haoliang, ZHOU Junwei. Mechanism study on tip leakage vortex in ducted propeller and a method to delay TLV cavitation[J]. Journal of Ship Mechanics, 2015, 19(12): 1445-1462. DOI: 10.3969/j.issn.1007-7294.2015.12.002 |
 2017, Vol. 49
2017, Vol. 49

 , 梅蕾
, 梅蕾