随着信息社会迅速发展,信道环境变得愈加复杂,对通信质量产生严重影响.为了改善系统性能,马可尼提出了MIMO (multiple-input multiple-output) 技术.该技术能够有效地利用空间资源[1],增加系统信道容量,提高传输速率和误码性能.空时分组码STBC (space time block code) 是一种能够获得最佳空间分集的编码方式[2-3]. Alamouti[4]基于STBC提出一种双天线发射方法来实现分集增益,由于其译码复杂度低已得到广泛应用.
近几年,分数傅里叶变换作为一种信号处理手段备受关注[5-8].加权分数傅里叶变换WFRFT (weighted-type fractional Fourier transform) 是由一系列函数加权求和得到的一种分数傅里叶形式[9].经过WFRFT变换后的信号具有抗干扰性强、能量分布均匀等优点.文献[10]提出一种基于WFRFT的混合载波数字通信系统,文献[11]验证了上述通信系统在选择性衰落信道下相比单载波、多载波系统具有更好的抗失真能力.文献[12]提出WFRFT与部分FFT相结合的混合载波系统,在快速时变信道下能有效抑制载波间干扰及多径干扰.文献[13]提出一种基于WFRFT的并行组合扩展系统,能够获得较高的宽带效率和系统安全性能.
从文献中能够看出,在很多场景下单载波和多载波体制已不是最佳选择,基于WFRFT的混合载波体制具有明显优势.混合载波信号是由原信号的时域、频域等形式的多分量信号组成,且各分量之间具有明确的数学约束关系.本文设计了一种基于WFRFT的2天线发射方法,将经过WFRFT变换后的信号分量按时频域信号合并为两路混合载波信号,经时延调整后由2根天线分别发射,接收端采用单天线接收处理.仿真对比结果表明本文提出的发射方法在系统误码性能及复杂度方面较有优势,能够有效抵抗信道衰落.
1 加权分数傅里叶变换在数字通信系统中,信号是离散形式的.本文采用适合离散信号的四项加权分数傅里叶变换.信号归一化的离散傅里叶变换DFT (discrete Fourier transform) 及逆变换IDFT (inverse discrete Fourier transform) 定义为
| $ \left\{ \begin{array}{l} X\left( k \right) = \frac{1}{{\sqrt N }}\sum\limits_{n = 0}^{N - 1} {x\left( n \right){{\rm{e}}^{ - {\rm{i}}\frac{{2\pi }}{N}kn}}} ,\\ x\left( n \right) = \frac{1}{{\sqrt N }}\sum\limits_{n = 0}^{N - 1} {X\left( k \right){{\rm{e}}^{ - {\rm{i}}\frac{{2\pi }}{N}kn}}} . \end{array} \right. $ |
对函数g(x) 分别进行0~3次离散傅里叶变换,结果可表示为g(x)、G(x)、g(-x) 和G(-x),称为g(x) 的基本态函数.
按照文献[9]的定义,四项加权分数傅里叶变换是由函数的4个基本态函数与对应系数线性加权得到,g(x) 的α阶WFRFT的表示形式为
| $ \begin{array}{l} {F^\alpha }\left[ {g\left( x \right)} \right] = {\omega _0}\left( \alpha \right)g\left( x \right) + {\omega _1}\left( \alpha \right)G\left( x \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\omega _2}\left( \alpha \right)g\left( { - x} \right) + {\omega _3}\left( \alpha \right)G\left( { - x} \right). \end{array} $ |
其中ω0(α)、ω1(α)、ω2(α) 和ω3(α) 是加权系数,表示为
| $ \begin{array}{l} {\omega _l}\left( \alpha \right) = \cos \left[ {\frac{{\left( {\alpha - l} \right)\pi }}{4}} \right]\cos \left[ {\frac{{\left( {\alpha - l} \right)\pi }}{2}} \right]\exp \left[ {\frac{{3\left( {\alpha - l} \right)\pi {\rm{i}}}}{4}} \right].\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;l = \left( {0,1,2,3} \right) \end{array} $ |
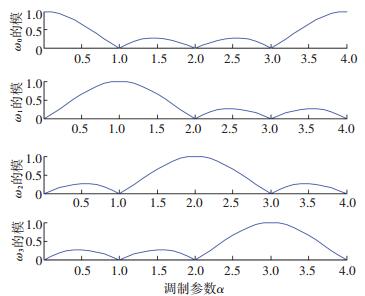
式中α为控制加权系数的调制参数,周期为4,范围设定为[0, 4) 或[-2, 2) 内的任意实数.加权系数随调制参数α的变化情况如图 1所示.
|
图 1 加权系数的模随调制参数α的变化规律 Figure 1 Magnitudes of the weighting coefficients as a function parameter α |
根据WFRFT的表达式可知,g(x) 通过离散傅里叶变换可以得到G(x),而g(x) 通过反转变换可以得到g(-x),四路信号彼此之间有数学上的约束关系.由图 1可知,当调制参数α=0时,Fα[g(x)]= g(x),信号的WFRFT变换后结果为原信号;当调制系数α=1时,Fα[g(x)]= G(x),信号的WFRFT变换后结果为原信号的傅里叶变换形式.
2 2天线发射方法 2.1 Alamouti空时码原理Alamouti在1998年提出了第一个空时分组码,发射的2个序列是正交的,能够为2天线发射系统提供完全的发射分集.第1个时隙内,天线1发射信号s1,天线2发射s2,第2个时隙内,天线1发射信号-s2*,天线2发射s1*,其编码矩阵为
| $ A = \left[ {\begin{array}{*{20}{c}} {{s_1}}&{ - s_2^ * }\\ {{s_2}}&{s_1^ * } \end{array}} \right]. $ |
假设在连续2个符号周期内信道不变,那么有
| $ \begin{array}{l} {h_1}\left( t \right) = {h_1}\left( {t + T} \right) = {h_1} = {\alpha _1}{{\rm{e}}^{{\rm{j}}\theta 1}},\\ {h_2}\left( t \right) = {h_2}\left( {t + T} \right) = {h_2} = {\alpha _2}{{\rm{e}}^{{\rm{j}}\theta 2}}. \end{array} $ |
接收端放置1根天线,接收到天线1和天线2的信号分别为
| $ \begin{array}{*{20}{c}} {{r_1} = r\left( t \right) = {h_1}{s_1} + {h_2}{s_2} + {n_1},}\\ {{r_2} = r\left( {t + T} \right) = - {h_1}s_2^ * + {h_2}s_1^ * + {n_2}.} \end{array} $ | (1) |
其中,n1和n2是均值为零,方差为σ2的复加性高斯白噪声.
合成接收端收到的信号为
| $ \begin{array}{l} {{s'}_1} = h_1^ * {r_{1 + }}{h_2}r_2^ * = \left( {{{\left| {{h_1}} \right|}^2} + {{\left| {{h_2}} \right|}^2}} \right){s_1} + \\ \;\;\;\;\;\;h_1^ * {n_{1 + }}{h_2}n_2^ * ,\\ {{s'}_2} = h_2^ * {r_{1 }} - {h_1}r_2^ * = \left( {{{\left| {{h_1}} \right|}^2} + {{\left| {{h_2}} \right|}^2}} \right){s_2} - \\ \;\;\;\;\;\;{h_1}n_{2 + }^ * h_2^ * {n_1}. \end{array} $ | (2) |
然后对s′1和s′2进行最大似然译码.
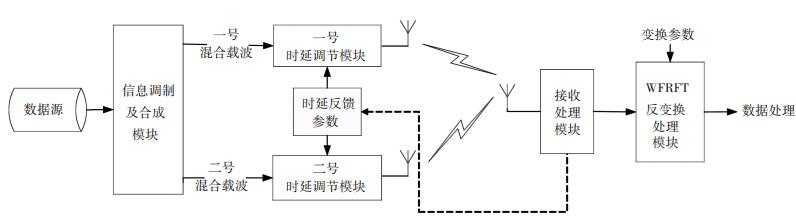
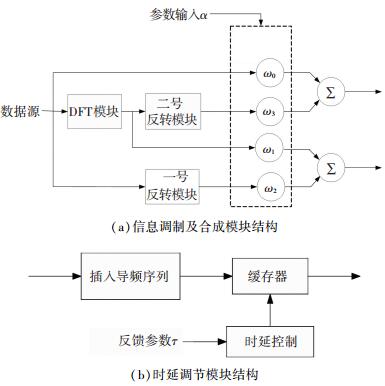
2.2 基于4-WFRFT的2天线发射方法本文提出一种基于四项加权分数傅里叶变换的2天线发射方法,该方法系统发射端有信息调制及合成模块、一号和二号时延调节模块、2根发射天线,接收端有1根接收天线、接收处理模块及WFRFT反变换处理模块,具体框图如图 2和图 3所示.
|
图 2 基于WFRFT的2天线发射系统结构 Figure 2 Framework of WFRFT based two-branch transmit system |
|
图 3 发射机内部结构 Figure 3 Structure of internal transmitter |
系统发射端采用2根发射天线,由以下步骤实现:
1) 将待发送信息送入信息调制及合成部分模块,该模块是本方法的核心部分.先对信号进行加权分数傅里叶变换的加权求和.该过程包括DFT模块、一号反转模块、二号反转模块和系数产生模块.通过模块变换后的四路信号分别与其对应加权系数ω0(α)、ω1(α)、ω2(α) 和ω3(α) 相乘,完成后送入合并模块.
2) 将原信号和依次经过DFT模块、二号反转模块的信号进行合并,得到一号混合载波信号分量;将原信号经过一号反转模块和经过DFT模块的信号进行合并,得到二号混合载波信号分量.
3) 将步骤2) 中产生的一号混合载波信号分量和二号混合载波信号分量分别送入一号、二号时延调节模块.
4) 时延调节模块先对输入信号分量插入导频序列,再送入缓存器进行时延调整.时延控制由接收端反馈的参数τ进行控制,完成时延调整的两路混合载波信号分别由2根天线发射,送入信道进行传输.
采用上述发射方法时,设待发送信号为g(n)(n=0, 1, …, 2N-1),经过时延调节模块后可得一号混合载波信号分量为
| $ {X_1}\left( n \right) = {\omega _0}\left( \alpha \right)g\left( n \right) + {\omega _3}\left( \alpha \right)G\left( { - n} \right), $ |
二号混合载波信号分量为
| $ {X_2}\left( n \right) = {\omega _1}\left( \alpha \right)G\left( n \right) + {\omega _2}\left( \alpha \right)g\left( { - n} \right). $ |
其中,G(n) 和G(-n) 为g(n) 和g(-n) 的经过傅里叶变换的表示形式. ω0(α)、ω1(α)、ω2(α) 和ω3(α) 是加权系数,表示为
| $ \begin{array}{*{20}{c}} {{\omega _l}\left( \alpha \right) = \cos \left[ {\frac{{\left( {\alpha - l} \right)\pi }}{4}} \right]\cos \left[ {\frac{{\left( {\alpha - l} \right)\pi }}{2}} \right]\exp \left[ {\frac{{3\left( {\alpha - l} \right)\pi {\rm{i}}}}{4}} \right].}\\ {l = \left( {0,1,2,3} \right)} \end{array} $ |
两路信号分量经过时延调整模块后,保证了接收端能够在同一时刻接收.
2.2.2 接收端的信号处理过程以接收端采用单天线接收为例,先将接收信号送入接收处理模块,反馈给发射端时延参数,同时将信号送入WFRFT反变换处理模块,完成后进行数据处理.
接收端接收的信号为
| $ R\left( n \right) = {h_0}\left( n \right){X_1}\left( n \right) + {h_1}\left( n \right){X_2}\left( n \right) + v\left( n \right), $ | (3) |
其中,v(n) 为加性高斯白噪声.将式 (1)、(2) 代入式 (3) 可得
| $ \begin{array}{l} R\left( n \right) = {h_0}\left( n \right)\left[ {{\omega _0}\left( \alpha \right)g\left( n \right) + {\omega _3}\left( \alpha \right)G\left( { - n} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;{h_1}\left( n \right)\left[ {{\omega _1}\left( \alpha \right)G\left( n \right) + {\omega _2}\left( \alpha \right)g\left( { - n} \right)} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;v\left( n \right). \end{array} $ |
经过-α阶的4-WFRFT变换可得原信号的估计值为
| $ \begin{array}{l} g'\left( n \right) = {F^{ - \alpha }}\left[ {R\left( n \right)} \right] = {F^{ - \alpha }}\left[ {{h_0}\left( n \right){X_1}\left( n \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {{h_1}\left( n \right){X_2}\left( n \right)} \right] + {F^{ - \alpha }}\left[ {v\left( n \right)} \right]. \end{array} $ |
本文提出发射方案的核心部分是信息调制及合成模块,该模块包含了四项加权分数傅里叶变换过程,得到的两路混合载波信号分量既含有时域信号又有频域信号,且彼此具有数学上的约束关系,能够补偿信道衰落带来的影响.而时延调节模块保证了接收端能够同时接收到两路信号,保证WFRFT反变换的顺利进行.
3 系统性能分析 3.1 传输速率分析通信过程中,传输速率会受到信道自由度的限制.如果不同的天线发送独立的不同码元,则可以充分利用全部的自由度,从而提高系统数据传输速率.
虽然Alamouti空时码2根天线在同一码元时间发送2个不同符号,但编码前输入的2个符号经过编码后输出的空时码长度也为2,2个不同符号仍需要2个码元时间才能完成发送.因此Alamouti空时码传输速率为2/2=1,所利用的自由度为1.而本文提出的2天线发射方法2根天线在同一时刻发射信息符号不同,但两路信号间具有数学关系.并且对接收端来说,两路信号之和才能恢复出原信号估计值,所以传输速率为2/2=1,所利用的自由度也是1.由此可见,两种发射方法在同一时刻发送信息符号数相同,具有相同的传输速率.
3.2 复杂度分析从文献[4]可知,Alamouti编码的复杂度与最大似然算法复杂度一致.整个发射系统的计算复杂度来自发射端信息调制及合成模块的计算,其中主要来自α阶4-WFRFT变换的计算. 4-WFRFT的结构主要包括DFT模块、反转模块及系数合并模块.计算每一个DFT模块需要用到FFT,需要O(NlogN) 的计算量;各支路输出信号与其加权系数相乘需要4个乘法运算,每个乘法运算需要O(N) 的计算量.在整个运算过程中,加法运算复杂度较低,可忽略不计. 表 1给出了实现基于WFRFT的2天线发射方法所需计算复杂度.
| 表 1 WFRFT发射方法的计算复杂度 Table 1 Computation complexity requirements of WFRFT based transmit method |
从表 1可以看出,本文提出的发射方法实现计算复杂度为O(Nlog N+4N).核心模块WFRFT部分可用快速傅里叶变换来实现,仅比DFT运算增加了系数的乘法运算部分,并且该复杂度的增加是非常有限的.
3.3 误码性能分析用MATLAB仿真出基于4-WFRFT的2天线发射方法过程并画出误码率曲线,与Alamouti编码2天线发射方法进行对比.
3.3.1 信道条件变化,WFRFT参数α不变采用调制方式为二进制相移键控调制BPSK (binary phase shift keying),WFRFT调制参数α取1.8,FFT点数128,假设系统同步精确,接收端采用单天线接收.信道采用文献[11]中“AWGN+时/频域滤波”简化选择性衰落信道模型.
在衰落信道下,影响系统误码性能的主要因素为时域、频域上的深衰落点以及噪声,而一般衰落点的影响是可以忽略的.因此,该信道模型是在时、频域上存在某些随机深衰落点,而其他点保持不变.采用这种信道模型能够更容易获取信道信息,从而可进行定性分析与理论分析.
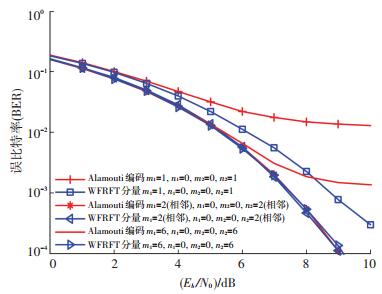
图 4给出了2种发射方法的2发1收系统在不同信道条件下的平均误比特率仿真结果. 图 4中mi代表第i条信道存在时域随机衰落点点数,nj代表第j条信道存在频域随机衰落点点数,随机衰落点均存在幅度衰落10 dB.
|
图 4 2发1收系统误码率对比 Figure 4 BER comparison of two-transmit-antennas and one-receive-antenna systems |
当m1=1, n1=0, m2=0, n2= 1时,2条信道均存在单点突发干扰,分别存在一个时域和频域随机衰落点.由图 4可以看出,该信道下基于WFRFT的2发1收发射方法比Alamouti编码的误码率曲线下降的更快,并始终低于Alamouti编码发射方法的误码率曲线,具有一定的优势.
而Alamouti编码应用条件要求信道衰落处于平坦衰落,需保证两相邻时刻内信道状态信息保持不变.当m1=2, n1=0, m2=0, n2= 2时,2个衰落点为相邻符号周期内的随机衰落点,此条件更适合Alamouti编码发射方法的应用,其误码性能相比信道仅存在单点突发干扰时大大提高了,并且能够与本文提出的发射方法误码率曲线基本重合,具有相同的误码性能,达到了分集效果.
随着信道环境变得恶劣,每条信道的随机衰落点数增加,当m1=6, n1=0, m2=0, n2=6且保证两相邻时刻内信道状态信息不变时,图 4给出2种发射方法的误码率曲线.相比前2种信道条件下曲线均有所上升,误码性能均变差,但基于WFRFT的2天线发射方法受影响较小.在符合Alamouti编码应用条件下,本文提出的发射方法误码率曲线仍能始终低于Alamouti编码发射方法,在恶劣环境下具有更稳定的抗衰落能力,能更好地抵抗信道衰落.
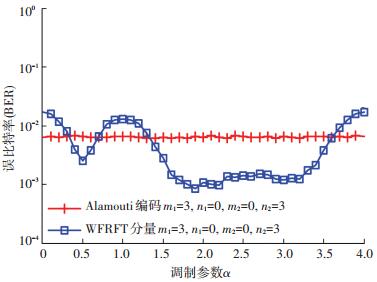
3.3.2 信道条件不变,WFRFT参数α变化WFRFT变换调制参数α具有周期性,范围一般设定为[0, 4) 内的任意实数.因此,当信道状态条件不变时,针对α取周期内不同值时的发射方法误码率曲线进行了仿真.
采用调制方式为BPSK,FFT点数128,假设系统同步精确,接收端采用单天线接收.信道采用文献[11]中“AWGN+时/频域滤波”简化选择性衰落信道模型.参数α取值范围从0到4,从0开始每隔0.1取一次值时,每次取值时需进行1 000次仿真,取Eb/N0= 8 dB时的平均误码率. 图 5为Eb/N0= 8 dB时系统误码率比较图. 图 5中mi代表第i条信道存在时域随机衰落点点数,nj代表第j条信道存在频域随机衰落点点数,每个随机衰落点均存在幅度衰落10 dB.
|
图 5 选择性衰落信道下Eb/N0=8 dB时误码率对比 Figure 5 BER comparison of different schemes over fading channels when Eb/N0= 8 dB |
当m1=3, n1=0, m2=0, n2= 3时,代表第1条信道为时域衰落,存在3个时域衰落点,第2条信道为频域衰落,存在3个频域衰落点,为满足Alamouti编码的适用条件,信道保证了两相邻时刻内信道状态信息不变.由于Alamouti编码不会随着α取值变化而受到影响,所以误码率是几乎不变的,曲线呈水平状.而4-WFRFT中的四路信号加权系数会随着α取值不同而变化,因此基于WFRFT的2天线发射方法的两路信号也会随着α取值变化而变化.
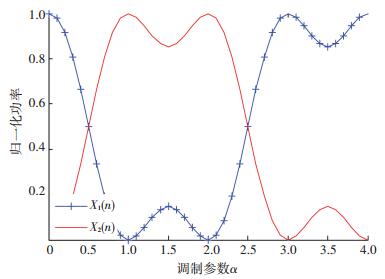
从图 5中可以看出,当α取值范围是 (0.3, 0.7) 和 (1.3, 3.5) 时,本文提出的发射方法误码率优于Alamouti编码发射方法.特别地,当α取[1.8, 3.3]内的数值时,其误码率大大低于Alamouti编码发射方法. 图 6为本文提出发射方法中两路发射信号归一化功率分布图.根据图 1和图 6,能够很好地解释图 5中误码率曲线的变化趋势.
|
图 6 两路发射信号归一化功率分布 Figure 6 Normalized power distribution of two branch transmitted signals |
由图 1和图 6可知,当α=0时,ω0(α)=1,发射信号只存在X1(n)=ω0(α) g(n),相当于发射端采用单天线进行发射,而第1条信道存在时域衰落,对X1(n) 影响非常大,导致其失真严重.因此,α=0时,本文提出的发射方法误码性能最差.同理可知,α=1时,该系统误码性能也同样最差.
当α取2附近的数值,如[1.8, 2.5]时,加权系数ω2(α) 的模趋近于1,其他加权系数值很小.在发射信号进行功率归一化时,X2(n) 因含有ω2(α)g(-n) 会被分配到较多的功率,并且主要呈现时域信号形式.而第2条信道存在频域衰落,对X2(n) 影响较小.因此,在α取值在[1.8, 2.5]范围内时,本文提出的发射方法信号误码率较低;类似地,当α取3附近数值[2.5, 3.3]时,加权系数ω3(α) 的模趋近于1,X1(n) 主要信号分量为ω3(α)G(-n) 且呈现频域信号形式.而第1条信道仅存在时域衰落,X1(n) 影响较小.因此,在α取值在[2.5, 3.3]范围时,本文提出的发射方法信号误码率也较低;在α∈[1.8, 3.3]时,基于WFRFT的2天线发射方法具有更好的误码性能.
当信道变得复杂,2条信道均是双弥散信道时,每条信道均既存在时域随机衰落点,又存在频域随机衰落点.为满足Alamouti编码应用条件,保证了两相邻时刻内信道状态信息不变.参数α取值范围从0到4,从0开始每隔0.1取一次值时,每次取值需进行1 000次仿真,得到Eb/N0为8 dB时的平均误码率.当Eb/N0=8 dB时,2发1收系统误码率比较图如图 7所示.

|
图 7 双弥散信道下Eb/N0=8 dB时误码率对比 Figure 7 BER comparison of different schemes over doubly-dispersive channels when Eb/N0= 8 dB |
由图 7可知,本文提出的发射方法的误码率曲线在α的周期取值内,始终低于基于Alamouti编码的发射方法,在双弥散信道下具有更优的误码性能,且优势明显.这是由于2条信道存在时域衰落,对Alamouti编码的信号影响较大.而信道因同时存在的频域衰落而变得复杂,所需的信道状态进行解码时也会有差错,这对信号恢复准确率影响较大.因此其误码率反而不如基于WFRFT的2天线发射方法.
由图 4~7仿真结果可知,本文提出的加权分数傅里叶2天线发射方法相对Alamouti发射方法具有更优的系统误码性能.本发射方法中,2根天线均发射混合载波信号,既含有时域信号,也含有频域信号,使信号的时频能量分布更均匀.在信道处于时频域均衰落时,受到畸变影响较小,并且两路混合载波信号间具有一定的数学约束关系.当某一信道产生畸变信号衰落严重时,其他信号的畸变会减小,从而能够降低误码率,提高恢复原发射信号的准确率.
此外,Alamouti空时码接收端需要已知信道信息进行解码,而本文提出WFRFT的2天线发射方法在接收端未知信道信息状态下,可直接对接收的信号进行加权分数傅里叶反变换,恢复出原发射信号信息.接收端解码处理更简单、方便.
4 结语本文提出一种基于加权分数傅里叶变换域的2天线发射方法,系统在信号发射前进行加权分数傅里叶变换,产生四路信号按时频信号合并方式将变换后的四路信号分量合并为两路混合载波信号,经时延调整后由2根发射天线发射.接收端采用单天线接收,通过WFRFT反变换模块可得到原发送信号的估计值.由于两路发射混合载波信号彼此间有数学约束关系,能量分布均匀的特性,能够充分地利用时频资源.仿真结果表明,在双弥散信道下,本文方法相比Alamouti空时码发射方法在系统误码率方面较有优势,能够有效抵抗信道衰落.特别地,随着信道条件变得越恶劣,这种优势越明显.同时,本文提出的发射方法设计复杂度较低,且接收端不需要信道状态信息,可直接将接收到的信息进行加权分数傅里叶反变换处理,得到原信号信息,接收端操作更加简单.
| [1] | ZHOU Xingyu, BAI Bo, CHEN Wei. Invited paper: antenna selection in energy efficient mimo systems: a survey[J]. China Communications, 2015, 12(9): 162-173. DOI: 10.1109/CC.2015.7275254 |
| [2] | TAROKH V, JAFARKHANI H, CALDERBANK A R. Space-time block coding for wireless communications: performance results[J]. IEEE Journal on Selected Areas in Communications, 1999, 17(3): 451-460. DOI: 10.1109/49.753730 |
| [3] | UYSAL M. Diversity analysis of space-time coding in cascaded rayleigh fading channels[J]. IEEE Communications Letters, 2006, 10(3): 165-167. DOI: 10.1109/LCOMM.2006.1603372 |
| [4] | ALAMOUTI S M. A simple transmit diversity technique for wireless communications[J]. IEEE Journal on Select Areas in Communication, 1998, 16(8): 1451-1458. DOI: 10.1109/49.730453 |
| [5] | PEI S C, DING J J. Relations between fractional operations and time-frequency distributions, and their applications[J]. IEEE Trans Signal Process, 2001, 49(8): 1638-1655. DOI: 10.1109/78.934134 |
| [6] | MEI Lin, ZHANG Qinyu, SHA Xuejun, et al. WFRFT precoding for narrowband interference suppression in DFT-based block transmission system[J]. IEEE Communications Letters, 2013, 17(10): 1916-1919. DOI: 10.1109/LCOMM.2013.090213.131126 |
| [7] |
刘晨, 沙学军, 张文彬, 等. 积分判决的高效协同信号调制解调方法[J].
哈尔滨工业大学学报, 2015, 47(3): 29-35.
LIU Chen, SHA Xuejun, ZHANG Wenbin, et al. An efficient signal modulation and demodulation method based on integral judgments[J]. Journal of Harbin Institute of Technology, 2015, 47(3): 29-35. DOI: 10.11918/j.issn.0367-6234.2015.03.005 |
| [8] | FANG Xiaojie, SHA Xuejun, MEI Lin. Guaranteeing wireless communication secrecy via a WFRFT-based cooperative system[J]. China Communications, 2015, 12(9): 76-82. DOI: 10.1109/CC.2015.7275261 |
| [9] | SHIH C C. Fractionalization of Fourier transform[J]. Optics Communications, 1995, 118(5/6): 495-498. DOI: 10.1016/0030-4018(95)00268-D |
| [10] | MEI Lin, SHA Xuejun, ZHANG Qinyu, et al. The concepts of hybrid-carrier scheme communication system[C]//The 6th International ICST Conference on Communications and Networking in China.Harbin: IEEE, 2011. |
| [11] | MEI Lin, SHA Xuejun, ZHANG Naitong. The approach to carrier scheme convergence based on 4-weighted fractional Fourier transform[J]. IEEE Communications Letters, 2010, 14(6): 503-505. DOI: 10.1109/LCOMM.2010.06.092413 |
| [12] | LI Yong, SHA Xuejun, WAND Kun. Hybrid carrier communication wih partial FFT demodulation over underwater acoustic channels[J]. IEEE Communications Letters, 2013, 17(12): 2260-2263. DOI: 10.1109/LCOMM.2013.102613.131651 |
| [13] | FANG Xiaojie, SHA Xuejun, LI Yong. Secret communication using parallel combinatory spreading WFRFT[J]. IEEE Communications Letters, 2015, 19(1): 62-65. DOI: 10.1109/LCOMM.2014.2359200 |
 2017, Vol. 49
2017, Vol. 49


