大规模多输入多输出 (Massive Multi-input Multi-output，Massive MIMO) 系统需要复杂的天线间同步技术及多条射频链路^[1]，导致系统的运算复杂度较高、能量消耗和硬件实现难度较大^[2].空间调制 (Spatial Modulation，SM) 技术是一种利用激活发射天线的序号和调制符号共同表示发射信息的新型传输方案，可完全消除空间多路MIMO系统中接收信号间的相互干扰，具有较高的传输速率.空间调制系统采用最大似然 (Maximum Likelihood，ML) 检测算法可获得最佳的误比特性能，但运算复杂度较高^[3].迫零算法 (ZF)、最小均方误差算法 (MMSE) 等次优算法虽然降低了运算复杂度，但误码性能较差^[4]，球形译码 (Sphere Decoding，SD) 算法可平衡系统运算复杂度和误比特两方面的性能^[5].文献[5-6]提出3种不同的空间调制下的球型译码算法，分别是：以接收端为中心的Rx-SD、以发射端为中心的Tx-SD和联合方案C-SD.在运算复杂度和误比特性能方面，C-SD始终优于Tx-SD，Rx-SD和C-SD在不同的情况下各有优劣，3种算法的运算复杂度都低于ML，误比特性能接近于ML.

在不影响空间调制系统误比特性能的前提下，为了进一步降低球型译码算法的运算复杂度，本文提出一种新的SM-SD算法，通过理论分析和仿真比较这种新算法与已有的Rx-SD、C-SD算法的运算复杂度和误比特性能.

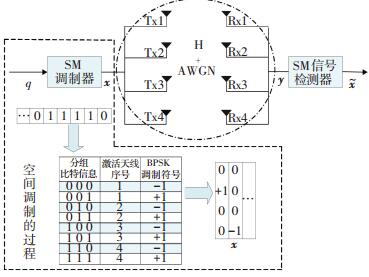
1 系统模型 1.1 空间调制系统模型

SM的基本思想是将待发送的信息分为两部分，一部分用于选择激活发射天线的序号，另一部分用于选择调制符号.假设SM系统发射天线数量为N_t，接收天线数量为N_r，调制符号集合中元素总数为M，发射机每次发送m=log₂(N_t)+log₂(M) 个二进制比特信息. log₂(N_t) 个比特信息由激活发射天线序号携带；log₂(M) 个比特信息由调制符号携带.为了不失一般性，这里的调制符号选取正交幅度调制 (Quadrature Amplitude Modulation，QAM).本文中，激活发射天线的序号用l_t表示，l_t∈{1, 2, …, N_t}，发射的调制符号用s_t表示，s_t∈{s₁, s₂, …, s_M}. 图 1是一个具有4根发射天线的SM系统模型，调制方式为BPSK. q是待发送的二进制序列，根据表格将q分组后产生含有4个元素的发射向量x，其中唯一的非零元素的位置表示被激活的发射天线的序号^[5].

在平坦慢衰落情况下，假设N_r×N_t维信道矩阵H中的每个元素相互独立，即各子信道相互独立，且服从均值为零与方差为1的复高斯分布，包络服从瑞利分布.假设每根接收天线上的噪声n为理想加性复高斯白噪声，噪声功率谱密度是已知的，符号能量为1，N_t维发射向量x_{lt, st}=[0_1×(lt-1), s_t, 0_1×(Nt-lt)]^T，N_r维的接收向量y为

$ \mathit{\boldsymbol{y = H}}{\mathit{\boldsymbol{x}}_{{l_{{\rm{t,}}}}{s_{\rm{t}}}}} + \mathit{\boldsymbol{n = }}{\mathit{\boldsymbol{h}}_{{l_{\rm{t}}}}}{\mathit{\boldsymbol{s}}_{\rm{t}}} + \mathit{\boldsymbol{n}}, $

(1)

式中h_lt位H的第l_t列.

1.2 球形译码算法

在不考虑噪声情况下，每一个发射向量x_{l, s}经过无线信道H之后对应着一个格点Hx_{l, s}，球型译码算法的思想是仅在以接收信号y为中心、以R为半径的球体中进行搜索，球体内与y之间欧几里得距离 (简称欧氏距离) 最小的格点对应于检测到的发射向量. SD算法的检测性能可以逼近ML，但不需要遍历搜索所有的格点，在半径R选择恰当的情况下，运算复杂度相对于ML会大大降低^[7].

SD算法实际上构造了一棵N_t层的搜索树，树中每一条路径{l, s}表示一个格点，对应着一个可能的发射向量，l为工作的发射天线序号且l∈{1, 2, …N_t}，s为发射符号且s∈{s₁, s₂, …, s_M}.路径的第一层对应发射向量的第N_t维，最后一层对应发射向量的第1维.本文将某一层的欧氏距离称为该层的“层欧氏距离”(下简称为层距)，而该层与它之前各层的层欧氏距离之和称为“部分欧氏距离”.

2 空间调制—球形译码算法 (SM-SD)

SM-SD算法根据{‖ y-Hx_{l, s}‖²≤R²}这一思想，仅通过搜索球内的可能发射向量来计算出激活发射天线的序号和发射的调制符号.本文将N_tM种发射信号向量组成的集合称为“发射搜索空间”，而“接收搜索空间”是接收向量的维数N_r.初始搜索半径与噪声方差σ_n²，N_r和系数α的乘积有关^[8]，即R²=αN_rσ_n².限定误比特率ε=10^-6，由$ 1-\frac{{\gamma ({N_{\rm{r}}}, {N_{\rm{r}}}\alpha )}}{{\Gamma ({N_{\rm{r}}})}} $=ε来确定初始半径R.

2.1 Rx-SD算法

Rx-SD遍历搜索“发射搜索空间”中所有的N_tM条路径，对每条路径从最高维开始不断地累加各维的层距，只要其仍然在球体之内，就继续在此路径上搜索，否则舍弃该条路径.每当发现一条球内的完整路径，就更新半径为此路径的欧氏距离.

Rx-SD中一条路径{l, s}只需要计算$ {{\tilde N}_{\rm{r}}} $(l, s) 次的层距，$ {{\tilde N}_{\rm{r}}} $ (l, s) 是使得{l, s}的欧氏距离开始超出R的最小累加次数，1≤$ {{\tilde N}_{\rm{r}}} $ (l, s)≤N_r.只有$ {{\tilde N}_{\rm{r}}} $ (l, s)=N_r且具有最小欧氏距离的路径才对应发射信号. Rx-SD可以表示为

$ \left[ {l_{\rm{t}}^{\left( {{\rm{Rx}} - {\rm{SD}}} \right)},s_{\rm{t}}^{\left( {{\rm{Rx}} - {\rm{SD}}} \right)}} \right] = \mathop {\arg \min }\limits_{\begin{array}{*{20}{c}} {l \in \left\{ {1,2, \cdots ,{N_{\rm{t}}}} \right\}}\\ {s \in \left\{ {{s_1},{s_2}, \cdots ,{s_M}} \right\}}\\ {{{\tilde N}_{\rm{r}}}\left( {l,s} \right) = {N_{\rm{r}}}} \end{array}} \left\{ {\sum\limits_{r = 1}^{{{\tilde N}_{\rm{r}}}\left( {l,s} \right)} {{{\left| {{y_r} - {h_{l,r}}s} \right|}^2}} } \right\}, $

式中y_r和h_{l, r}分别表示y和h_l的第r维元素.根据文献[2]，Rx-SD算法减小了“接收搜索空间”，非常适用于N_r非常大的情况.

2.2 C-SD算法

接收信号、发送信号和噪声均为复向量，为了简化计算，首先需要对y, H, x_{lt, st}进行实数化，转变为高维的实数向量y, H, x_{l, s}.式 (1) 转化为

$ \mathit{\boldsymbol{\bar y = \bar H}}{{\mathit{\boldsymbol{\bar x}}}_{{l_{{{t,}}}}{s_{{t}}}}} + \mathit{\boldsymbol{\bar n}} $

式中：$ \mathit{\boldsymbol{\bar y = }}{\left[{\Re \{ \mathit{\boldsymbol{y}}\}, \Im \{ \mathit{\boldsymbol{y}}\} } \right]^{\rm{T}}} $，$\mathit{\boldsymbol{\bar H = }}\left[{\begin{array}{*{20}{c}} {\Re (\mathit{\boldsymbol{H}})} & {-\Im (\mathit{\boldsymbol{H}})}\\ {\Im (\mathit{\boldsymbol{H}})} & {\Re (\mathit{\boldsymbol{H}})} \end{array}} \right] $，${{\mathit{\boldsymbol{\bar x}}}_{{l_t},{s_t}}} = {\left[ {\Re ({\mathit{\boldsymbol{x}}_{{l_t},{s_t}}}),\Im ({\mathit{\boldsymbol{x}}_{{l_t},{s_t}}})} \right]^{\rm{T}}} $, $\mathit{\boldsymbol{\bar n = }}{\left[{\Re (\mathit{\boldsymbol{n}}), \Im (\mathit{\boldsymbol{n}})} \right]^{\rm{T}}} $, $\Re ( \bullet ) $和$ \Im ( \bullet )$分别表示取括号内变量的实部和虚部^[9].

C-SD算法同时减小“发射搜索空间”和“接收搜索空间”，它只计算位于球体内的格点的欧氏距离，并不断更新搜索半径，节省了层距的计算次数.设Θ_R是位于球体内部的发射向量的集合，C-SD可以写成

$ \left[ {l_{\rm{t}}^{\left( {{\rm{C}} - {\rm{SD}}} \right)},s_{\rm{t}}^{\left( {{\rm{C}} - {\rm{SD}}} \right)}} \right] = \mathop {\arg \min }\limits_{\left( {l,s} \right) \in {\Theta _R}} \left\{ {{{\left\| {\bar y - \bar H{{\bar x}_{l,s}}} \right\|}^2}} \right\}. $

(2)

考虑N_t≤N_r的超定系统，$ \mathit{\boldsymbol{\bar G = }}{{\mathit{\boldsymbol{\bar H}}}^{\rm{T}}}\mathit{\boldsymbol{\bar H}}$是正定的，由Cholesky分解有$ \mathit{\boldsymbol{\bar G = \bar P}}{{\mathit{\boldsymbol{\bar P}}}^{\rm{T}}} $，P是2N_t×2N_r的上三角矩阵^[2].所以C-SD可转化为

$ \left[ {l_{\rm{t}}^{\left( {{\rm{C}} - {\rm{SD}}} \right)},s_{\rm{t}}^{\left( {{\rm{C}} - {\rm{SD}}} \right)}} \right] = \mathop {\arg \min }\limits_{\left( {l,s} \right) \in {\Theta _R}} \left\{ {{{\left\| {\bar z - \bar P{{\bar x}_{l,s}}} \right\|}^2}} \right\}, $

式中z =PG^-1 H^Ty.

由于发射端只激活了第l根发射天线，所以发射复向量中只有一个非零元素，实数化后的发射向量x_{l, s}中有两个非零元素，即发射符号s_t的虚部$ \Im $(s_t) 和实部$ \Re $(s_t)，分别位于x_{l, s}的第l+N_t维和第l维，x_{l, s}其他维度上的元素均为0.

C-SD首先计算两个非零元素所在各自维度上的取值区间，然后从“发射搜索空间”中寻找满足取值区间的发射向量组成集合Θ_interval，取值区间为

$ \begin{array}{l} \frac{{ - R' + {{\bar z}_{l,{N_{\rm{t}}}}}}}{{{{\bar P}_{l + {N_{\rm{t}}},l + {N_{\rm{t}}}}}}} \le \Im \left( s \right) \le \frac{{R' + {{\bar z}_{l,{N_{\rm{t}}}}}}}{{{{\bar P}_{l + {N_{\rm{t}}},l + {N_{\rm{t}}}}}}},\\ \frac{{ - R'' + {{\bar z}_{l\left| {l + {N_{\rm{t}}}} \right.}}}}{{{{\bar P}_{l,l}}}} \le \Re \left( s \right) \le \frac{{R'' + {{\bar z}_{l\left| {l + {N_{\rm{t}}}} \right.}}}}{{{{\bar P}_{l,l}}}}. \end{array} $

(3)

式中：$ {{\bar z}_{a|b}} = {{\bar z}_a}-{{\bar P}_{a, b}}\Im (s) $，$ {{R'}^2} = {R^2}-\sum\limits_{m = l + {N_{\rm{t}}} + 1}^{2{N_{\rm{t}}}} {|{{\bar z}_m}{|^2}} $，${{\Re ''}^2} ={{R'}^2}- \sum\limits_{v = l + 1}^{l + {N_{\rm{t}}}} {\bar z_{v|l + {N_{\rm{t}}}}^2} $，P_{a, b}表示矩阵P的第a行第b列的元素，z_a表示向量z的第a维元素.接下来，检验集合Θ_interval内各发射向量的欧式总距离，检验门限开始时设为初始半径，每当找到了一个发射向量的欧氏总距离小于门限，就更新检验门限为欧氏总距离，继续搜索Θ_interval内其他发射向量.

3 新SM-SD算法 3.1 新型实数化方式

SD中H的结构限制了搜索必须从第一层开始逐层向下进行，并且在计算第k维 (k=l+N_t-1, …, 1) 的层距$ |{{\bar z}_k}{\rm{-}}\sum\limits_{m = k}^{2{N_{\rm{t}}}} {{{\bar P}_{k, m}}{{\bar x}_m}} {{\rm{|}}^2}$时要利用x_{l, s}第l+N_t维的元素x_l+Nt，即检测x_l时受到x_l+Nt的影响.现在将实数信道矩阵修改为

$ \begin{array}{l} \mathit{\boldsymbol{\tilde H = }}\\ \left[ {\begin{array}{*{20}{c}} {\Re \left( {{H_{1,1}}} \right)} & { - \Im \left( {{H_{1,1}}} \right)} & \cdots & {\Re \left( {{H_{1,{N_{\rm{t}}}}}} \right)} & { - \Im \left( {{H_{1,{N_{\rm{t}}}}}} \right)}\\ {\Im \left( {{H_{1,1}}} \right)} & {\Re \left( {{H_{1,1}}} \right)} & \cdots & {\Im \left( {{H_{1,{N_{\rm{t}}}}}} \right)} & {\Re \left( {{H_{1,{N_{\rm{t}}}}}} \right)}\\ \vdots & \vdots & \ddots & \vdots & \vdots \\ {\Re \left( {{H_{{N_{\rm{r}}},1}}} \right)} & { - \Im \left( {{H_{{N_{\rm{r}}},1}}} \right)} & \cdots & {\Re \left( {{H_{{N_{\rm{r}}},{N_{\rm{t}}}}}} \right)} & { - \Im \left( {{H_{{N_{\rm{r}}},{N_{\rm{t}}}}}} \right)}\\ {\Im \left( {{H_{{N_{\rm{r}}},1}}} \right)} & {\Re \left( {{H_{{N_{\rm{r}}},1}}} \right)} & \cdots & {\Im \left( {{H_{{N_{\rm{r}}},{N_{\rm{t}}}}}} \right)} & {\Re \left( {{H_{{N_{\rm{r}}},{N_{\rm{t}}}}}} \right)} \end{array}} \right]. \end{array} $

(4)

式中: H_{m, n}是从第n根发射天线到第m根接收天线间的增益^[10]，n∈{1, 2, …, N_t}，m∈{1, 2, …, N_r}.相应的，SM的实数发射向量x_{lt, st}中元素的检测顺序发生改变，两个非零元素的位置相邻，分别位于第2l-1维和第2l维. x_{lt, st}的形式为

$ {{\mathit{\boldsymbol{\bar x}}}_{{l_{\rm{t}}},{s_{\rm{t}}}}} = \left[ \begin{array}{l} 0\\ \vdots \\ \Re \left( s \right)\\ \Im \left( s \right)\\ \vdots \\ 0 \end{array} \right]\begin{array}{*{20}{c}} 1\\ \vdots \\ {2l - 1}\\ {2l}\\ \vdots \\ {第2{N_{\rm{t}}}维} \end{array} $

对$ {\mathit{\boldsymbol{\tilde H}}} $进行QR分解：$ \mathit{\boldsymbol{\tilde H = Q}}\left[{\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\bar D}}}\\ {{{\bf{0}}_{(2{N_{\rm{r}}}-{N_{\rm{t}}}) \times 2{N_{\rm{t}}}}}} \end{array}} \right] $，其中D为2N_t×2N_t维的上三角矩阵，Q为2N_r×2N_r维的正交矩阵，且Q =[Q ₁ Q ₂]，Q ₁和Q ₂分别是2N_r×2N_t维和2N_r×(2N_r-2N_t) 维的矩阵^[11]. D具有稀疏性，当k=1, 3, …, 2N_t-1时，D的第k行第k+1列的元素D_{k, k+1}=0. D形式为

$ \mathit{\boldsymbol{\tilde D = }}\left[ {\begin{array}{*{20}{c}} {{{\bar D}_{1,1}}} & 0 & {{{\bar D}_{1,3}}} & \cdots & {{{\bar D}_{1,2{N_{\rm{t}}}}}}\\ 0 & {{{\bar D}_{2,2}}} & {{{\bar D}_{2,3}}} & \cdots & {{{\bar D}_{2,2{N_{\rm{t}}}}}}\\ \vdots & \vdots & \ddots & \cdots & \vdots \\ 0 & 0 & 0 & {{{\bar D}_{2{N_{\rm{t}}} - 1,2{N_{\rm{t}}} - 1}}} & 0\\ 0 & 0 & 0 & 0 & {{{\bar D}_{2{N_{\rm{t}}},2{N_{\rm{t}}}}}} \end{array}} \right]. $

这种稀疏性使搜索树的相邻两层相互独立，在计算层距时互不影响，减少了乘法运算次数.搜索树共有2N_t层，由前面可知，搜索树的第一层对应实数发射向量的第2N_t维，第二层对应着发射向量的第2N_t-1维，以此类推.例如，第2层的层距|z_2Nt-1-D_{2Nt-1, 2Nt-1} x_2Nt-1| ²不受第1层中x_2Nt影响，实乘的运算次数比C-SD减少1次.

3.2 新SM-SD算法原理

式 (3) 中的各向量已经分别转化为实向量

$ \begin{array}{l} {{\mathit{\boldsymbol{\bar x}}}_{l,s}} = {\left[ {0 \cdots \Re \left( s_{\rm{t}} \right),\Im \left( s_{\rm{t}} \right) \cdots 0} \right]^{\rm{T}}},\\ \mathit{\boldsymbol{\bar y = }}{\left[ {\Re \left( {{y_1}} \right),\Im \left( {{y_2}} \right) \cdots \Re \left( {{y_{{N_{\rm{r}}}}}} \right),\Im \left( {{y_{{N_{\rm{r}}}}}} \right)} \right]^{\rm{T}}},\\ \mathit{\boldsymbol{\bar n = }}{\left[ {\Re \left( {{n_1}} \right),\Im \left( {{n_1}} \right) \cdots \Re \left( {{n_{{N_{\rm{r}}}}}} \right),\Im \left( {{n_{{N_{\rm{r}}}}}} \right)} \right]^{\rm{T}}}. \end{array} $

式 (4) 中的$ {\mathit{\boldsymbol{\tilde H}}} $转化为${\mathit{\boldsymbol{\bar H}}} $.对$ {\mathit{\boldsymbol{\bar H}}} $进行QR分解后，由$ {\left\| {\mathit{\boldsymbol{\bar y-\bar H}}{{\mathit{\boldsymbol{\bar x}}}_{l, s}}} \right\|^2} \le {R^2} $得到

$ {\left\| {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{Q}}_1^H}\\ {\mathit{\boldsymbol{Q}}_2^H} \end{array}} \right]\mathit{\boldsymbol{\bar y}} - \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\bar D}}}\\ {\bf{0}} \end{array}} \right]{{\mathit{\boldsymbol{\bar x}}}_{l,s}}} \right\|^2} \le {R^2}. $

忽略$ {\left\| {{\mathit{\boldsymbol{Q}}_2}^{\rm{H}}\mathit{\boldsymbol{\bar y}}} \right\|^2} $项的影响，设2N_t维向量$ \mathit{\boldsymbol{\bar z = }}{\mathit{\boldsymbol{Q}}_1}^{\rm{H}}\mathit{\boldsymbol{\bar y}} $，位于球内的发射向量必须满足

$ \sum\limits_{i = 1}^{2{N_{\rm{t}}}} {{{\left[ {{{\bar z}_i} - \sum\limits_{j = i}^{2{N_{\rm{t}}}} {{{\bar D}_{i,j}}{{\bar x}_{l,s}}\left( j \right)} } \right]}^2}} \le {R^2}. $

(5)

式中x_{l, s}(j) 表示向量x_{l, s}的第j维元素.

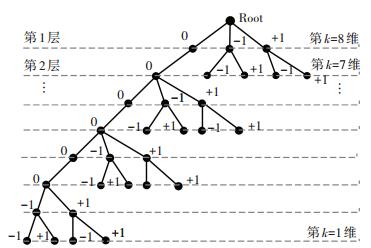
定义z，x_{l, s}的第2N_t维分量对应着码搜索树的第1层，第2N_t-1维分量为第2层，依次类推，所以搜索树的第i层对应向量z，x_{l, s}的第k=2N_t-i+1维分量. 图 2为4×4且采用4QAM的SM系统的码搜索树结构.

在新SM-SD算法中，当i≥3时，能进行到第i层 (第k=2N_t-i+1维) 的点必然满足在第i-1层和第i-2层中有x_{l, s}(2N_t-i+2)=0和x_{l, s}(2N_t-i+3)=0；当i=1, 2时，并不存在x_{l, s}(2N_t-i+2) 和x_{l, s}(2N_t-i+3)，所以直接计算第1层和第2层，如果有x_{l, s}(2N_t)=0和x_{l, s}(2N_t-1)=0，则计算第3层.

3.3 新SM-SD算法的步骤

此算法从搜索树第1层 (i=1) 开始执行以下步骤.初始条件下，假设所有发射向量构成一个集合ϕ₁，再定义一个ϕ₂为空集，将来用于保存与接收向量之间具有最小欧式距离的发射向量.

Step 1 根据式 (5)，在第i层计算x_{l, s}(2N_t-i+1) 的可取值.

x_{l, s}(2N_t-i+1) 的取值范围为

$ \frac{{ - R' + {{\bar z}_{2{N_{\rm{t}}} - i + 1}}}}{{{{\bar D}_{2{N_{\rm{t}}} - i + 1,2{N_{\rm{t}}} - i + 1}}}} \le {{\bar x}_{l,s}}\left( {2{N_{\rm{t}}} - i + 1} \right) \le \frac{{R' + {{\bar z}_{2{N_{\rm{t}}} - i + 1}}}}{{{{\bar D}_{2{N_{\rm{t}}} - i + 1,2{N_{\rm{t}}} - i + 1}}}}, $

(6)

式中$ {{R'}^2} = {R^2}-\sum\limits_{m = 2{N_{\rm{t}}}-i + 2}^{2{N_{\rm{t}}}} {|{{\bar z}_m}{|^2}} $.

遍历集合ϕ₁中的发射向量之后:

① 如果ϕ₁中任何一个发射向量的x_{l, s}(2N_t-i+1) 都不满足式 (6):

a) 如果集合ϕ₂为空集，则增大半径R，令i=1，ϕ₁存入全部发射向量，重新回到Step 1；

b) 如果集合ϕ₂为非空集，则算法结束，ϕ₂中唯一发射向量即是发射信号.

② 如果集合ϕ₁中存在发射向量的x_{l, s}(2N_t-i+1) 满足式 (6)，则去掉ϕ₁中不满足式 (6) 的发射向量，执行Step 2.

Step 2 对集合ϕ₁中每个发射向量的x_{l, s}(2N_t-i+1) 的取值情况进行判断.

① 如果ϕ₁中全部发射向量满足x_{l, s}(2N_t-i+1)≠0，则对每个向量执行Step 3，执行完毕后，ϕ₁为空，使用与Step 1中① 相同的方法对ϕ₂进行判断.

② 如果ϕ₁中一部分发射向量满足x_{l, s}(2N_t-i+1)≠0，另一部分发射向量不满足x_{l, s}(2N_t-i+1)≠0，则对于满足x_{l, s}(2N_t-i+1)≠0的每一个发射向量，都执行Step 3，对于x_{l, s}(2N_t-i+1)=0的向量不做处理；ϕ₁中全部向量判断完毕后，令i=i+2.

a) 若i≤2N_t，说明还没有搜索到搜索树最后两层，则返回到Step 1.

b) 若i>2N_t，所有情况均已考虑完毕，集合ϕ₁显然已为空，对集合ϕ₂进行判断.若ϕ₂非空，则算法结束，若ϕ₂仍为空，则增大半径R，令i=1，ϕ₁装入全部发射向量.

Step 3 若某个发射向量满足x_{l, s}(2N_t-i+1)≠0，根据式 (5)，则该发射向量中x_{l, s}(2N_t-i) 的取值范围为

$ \frac{{ - R'' + {{\bar z}_{2{N_{\rm{t}}} - i}}}}{{{{\bar D}_{2{N_{\rm{t}}} - i,2{N_{\rm{t}}} - i}}}} \le {{\bar x}_{l,s}}\left( {2{N_{\rm{t}}} - i} \right) \le \frac{{R'' + {{\bar z}_{2{N_{\rm{t}}} - i}}}}{{{{\bar D}_{2{N_{\rm{t}}} - i,2{N_{\rm{t}}} - i}}}}. $

(7)

式中

$ {R^{''2}} = {R^{'2}} - {\left| {{{\bar z}_{2{N_{\rm{t}}} - i + 1}} - {{\bar D}_{2{N_{\rm{t}}} - i + 1,2{N_{\rm{t}}} - i + 1}}{{\bar x}_{l,s}}\left( {2{N_{\rm{t}}} - i + 1} \right)} \right|^2}. $

① 如果这个发射向量的x_{l, s}(2N_t-i) 不满足式 (7)，则从集合ϕ₁中去除这个发射向量，然后返回到Step 2.

② 如果这个发射向量的x_{l, s}(2N_t-i) 满足式 (7)，说明找到一个满足取值区间条件的发射向量，保存在集合Θ_interval中.需要以R来检验此发射向量的欧几里得总距离，计算第i+1层的部分欧氏距离:

$ \begin{array}{l} {w_{i + 1}} = \sum\limits_{m = 2{N_{\rm{t}}} - i + 2}^{2{N_{\rm{t}}}} {{{\left| {{{\bar z}_m}} \right|}^2} + \left| {{{\bar z}_{2{N_{\rm{t}}} - i + 1}} - } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\;{\left. {{{\bar D}_{2{N_{\rm{t}}} - i + 1,2{N_{\rm{t}}} - i + 1}}{{\bar x}_{l,s}}\left( {2{N_{\rm{t}}} - i + 1} \right)} \right|^2} + \\ \;\;\;\;\;\;\;\;\;\;\;\;{\left| {{{\bar z}_{2{N_{\rm{t}}} - i}} - {{\bar D}_{2{N_{\rm{t}}} - i,2{N_{\rm{t}}} - i}}{{\bar x}_{l,s}}\left( {2{N_{\rm{t}}} - i} \right)} \right|^2}. \end{array} $

(8)

如果此时集合ϕ₂为空，则令检验门限M=R².如果w_i+1＞M，则从集合ϕ₁中去除此发射向量，返回Step 2；如果w_i+1＜M，检验欧几里得总距离.

$ \begin{array}{l} {w_{i + 1}} + \sum\limits_{m = 1}^{2{N_{\rm{t}}} - i - 1} {\left| {{{\bar z}_m} - {{\bar D}_{m,2{N_{\rm{t}}} - i}}{{\bar x}_{l,s}}\left( {2{N_{\rm{t}}} - i} \right) - } \right.} \\ \;\;\;\;\;\;\;{\left. {{{\bar D}_{m,2{N_{\rm{t}}} - i + 1}}{{\bar x}_{l,s}}\left( {2{N_{\rm{t}}} - i + 1} \right)} \right|^2} \le M. \end{array} $

(9)

在累加计算过程中，一旦发现累加和不满足式 (9)，则将之从ϕ₁中删去，返回Step 2.若总距离＜M，则得到一个球内的点，对应的发射向量为x_{l, s}=(0, …0, x_{l, s}(2N_t-i+1), x_{l, s}(2N_t-i), 0, …, 0)^T，用它替换集合ϕ₂中原来的发射向量.更新判决门限M为此向量的欧几里得总距离，并将此向量从ϕ₁中删去.返回Step2.

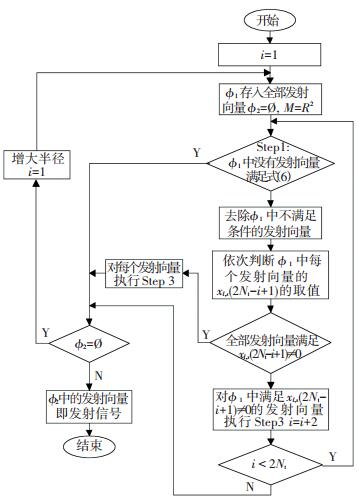
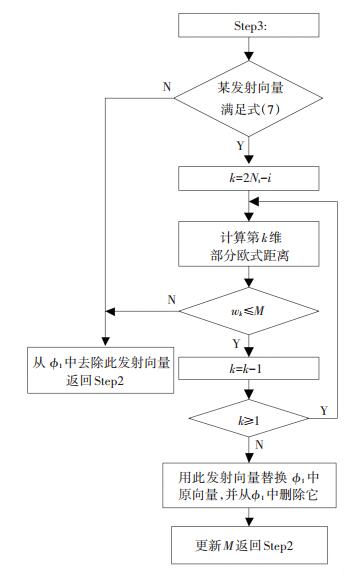
新SM-SD算法执行过程可以由图 3和图 4中的流程图来表示.

4 SM-SD算法运算复杂度分析

运算复杂度可以用算法过程中实数乘法运算的数量来衡量 (本文中，除法也看作乘法)，下面对各算法 (SM-ML、Rx-SD、C-SD、新SM-SD算法) 的实乘运算次数进行分析.

4.1 SM-ML算法

可能发射向量的总数是N_tM，$ \left\| {\mathit{\boldsymbol{y}}-{\mathit{\boldsymbol{h}}_l}s} \right\|_F^2 = {\Re ^2}(\mathit{\boldsymbol{y-}}{\mathit{\boldsymbol{h}}_l}s) + \Im ^2(\mathit{\boldsymbol{y-}}{\mathit{\boldsymbol{h}}_l}s) $需要6N_r次实乘，其中h_ls需要4N_r次实乘^[12].因此，SM-ML的运算复杂度为6N_rN_tM.

4.2 Rx-SD算法

Rx-SD算法对一条路径{l, s}需要进行${{\tilde N}_{\rm{r}}} $(l, s) 欧氏距离运算，计算‖ y - h_ls‖²中每一层的欧氏距离需要6次实乘.因此，Rx-SD的运算复杂度为$ 6\sum\limits_{l = 1}^{{N_{\rm{t}}}} {\sum\limits_{s = 1}^M {{{\tilde N}_{\rm{r}}}(l, s)} } $.

4.3 C-SD算法

C-SD的运算复杂度就是计算球内点集Θ_R的复杂度，运算复杂度为C_C-SD=C_pre-com+C_interval+C_check.

1) C-SD需要预先复杂度，包括Cholesky分解以及计算G，z，ρ的运算复杂度，即

$ {C_{{\rm{pre - com}}}} = {C_{CH}} + {C_{\mathit{\boldsymbol{\bar G}}}} + {C_\rho } + {C_{\bar z}}. $

式中：C_CH=4N_t³/3，C_ρ=4N_t²(2N_t+2N_r)+((2N_t)³+ 3(2N_t)²+2(2N_t))/3，C_z=4N_tN_r，C_G =2N_t(4N_rN_t+1).

2) C-SD的计算取值区间以及检验过程的运算复杂度为

$ \begin{array}{l} {C_{{\rm{interval}}}} + {C_{{\rm{check}}}} = \sum\limits_{l = 1}^{{N_{\rm{t}}}} {\left[ {\left( {{N_{\rm{t}}} - l + 2} \right) + \left( {2{N_{\rm{t}}} + 3} \right) \times } \right.} \\ \;\;\;\;\;\;\left. {{N_{\left( 1 \right)}}} \right] + 3\sum\limits_{\left( {l,s} \right) \in {\mathit{\Theta }_{{\rm{interval}}}}} {\tilde L\left( {l,s} \right)} . \end{array} $

其中，N₍₁₎为C-SD算法中计算式 (3) 的次数，$ {\tilde L} $(l, s) 为检验集合Θ_interval中格点{l, s}所需的欧几里得运算次数，$ {\tilde L} $ (l, s) 取1, 2, …, l中的某一个值.

4.4 新SM-SD算法

新SM-SD算法的运算复杂度包括：预先复杂度C_pre-com，求取值区间的复杂度C_interval和检验Θ_interval内格点的欧几里得总距离的运算复杂度C_check.

1) 预先复杂度为C_pre-com=C_QR+C_z +C_‖Q2^Hy‖²，QR分解的复杂度为

$ {C_{{\rm{QR}}}} = \sum\limits_{k = 1}^N {\left[ {2f\left( k \right) + {f^2}\left( k \right) + 2{f^3}\left( k \right) + 1} \right] - N_{\rm{r}}^3} . $

式中：f(k)=N_r+1-k，N=min{N_r-1, N_t}^[13]，C_{‖Qz^Hy‖²}=(2N_r-2N_t)(2N_r+1)，C_z =4N_tN_r.

2) 计算取值区间和检验Θ_interval内格点欧几里得总距离的运算复杂度为

$ \begin{array}{l} {C_{{\rm{interval}}}} + {C_{{\rm{check}}}} = \sum\limits_{i \in \left( {1,3, \cdots 2{N_{\rm{t}}} - 1} \right)} {{M_{\left( i \right)}}\left[ {4 + 4{N_{\left( i \right)}} + } \right.} \\ \;\;\;\;\;\left. {\sum\limits_{\left( {l,s} \right) \in {\mathit{\Theta }_{{\rm{interval}}}}} {\left( {3\tilde L\left( {l,s} \right) + 2} \right)} } \right] - 2. \end{array} $

其中，N_(i)是码搜索树第i层区间内非零可取值的个数，Θ_interval为满足两层取值区间条件的格点构成的点集，0≤ $ {\tilde L}$ (l, s)≤(2N_t-i-1). M_(i)取值为0或者1，当i=1时，M₍₁₎=1.当i≠1时，若在第 (i-2) 层中x_{l, s}(2N_t-i+3) 的可取值含零，则M_(i)=1, 否则，M_(i)=0.

解释：

1) 假设在搜索过程中，在码搜索树的第i∈(1, 3, …2N_t-1) 层，具有N₍i) 个非零可取值.

当i=1时，计算式 (6) 中取值区间需要2次实除；对于N₍₁₎个非零的x_{l, s}(2N_t)，计算式 (7) 中的取值区间需要2次实乘 (计算R′)，2次实除.

当i=3，5…，2N_t-1时，计算式 (6) 中取值区间需要2次实除，2次实乘 (计算R′).对于N_(i)个非零的x_{l, s}(2N_t-i+1)，计算式 (7) 中的取值区间时需要2次实除，2次实乘 (计算R″).所以有

$ {C_{{\rm{interval}}}} = \sum\limits_{i \in \left( {1,3, \cdots 2{N_{\rm{t}}} - 1} \right)} {\left[ {4 + 4{N_{\left( i \right)}}} \right]} - 2. $

2) 在检验Θ_interval中的格点{l, s}的欧几里得总距离时，第2N_t维到第 (2N_t-i+1) 维的层欧氏距离已经计算过，计算第 (2N_t-i) 维的层欧氏距离需要2次实乘，从第 (2N_t-i-1) 维到第1维需要计算$ {\tilde L} $ (l, s) 层，每层需要3次实乘.所以检验过程中的运算复杂度为

$ {C_{{\rm{check}}}} = \sum\limits_{i \in \left( {1,3, \cdots 2{N_{\rm{t}}} - 1} \right)} {\sum\limits_{\left( {l,s} \right) \in {\mathit{\Theta }_{{\rm{interval}}}}} {\left[ {3\tilde L\left( {l,s} \right) + 2} \right]} } . $

3) 只有当第 (i-2) 层中x_{l, s}(2N_t-i+3) 的可取值含有零时，新SM-SD算法才会执行到第i层，所以用M_(i)表示在码搜索树的第 (i-2) 层中的可取值是否含有零，M_(i)取值为0或者1.

5 仿真结果分析 5.1 仿真设置及说明

在仿真实验中，选取了多个发射天线数N_t、接收天线数N_r和调制尺寸M不同的SM系统，接收端采用新SM-SD、Rx-SD、C-SD和SM-ML算法，信道矩阵元素服从 (0，1) 复高斯分布，噪声为加性高斯白噪声，符号能量为1，通过改变噪声的功率谱密度来设置信噪比在0至20 dB的范围内. SD的初始搜索半径是在ε=10^-6这一条件下根据R²=2αN_rσ_n²来选取.这里用“信道接入速率”表示单位时间内发射端发送的二进制比特数，用m表示，单位为“bit/信道接入”.

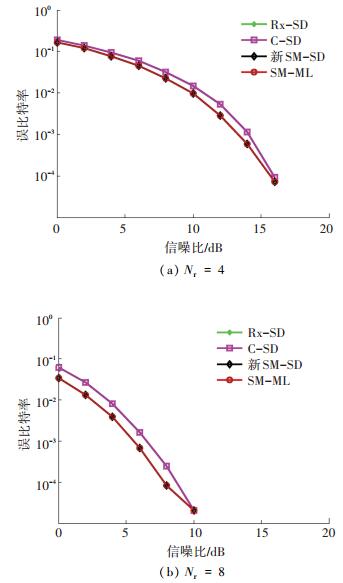
5.2 误比特率仿真

图 5是N_t=N_r=4，采用16QAM的SM系统和N_t≠N_r，m=6的SM系统的BER.仿真结果表明：新SM-SD和Rx-SD算法的误比特性能与SM-ML几乎完全相同，在相同的误比特率条件下 (例如取10^-4)，C-SD算法所需要的信噪高于新SM-SD约1 dB.

5.3 运算复杂度仿真

在比较运算复杂度时，将新SM-SD、Rx-SD和C-SD算法的运算复杂度用相对于SM-ML算法的减少量C_rel来表示，C_rel越大表示运算复杂度越低.

$ {C_{{\rm{rel}}}}\left( \% \right) = 100 \times \frac{{{C_{{\rm{SM - ML}}}} - {C_{{\rm{SM - SD}}}}}}{{{C_{{\rm{SM - ML}}}}}}. $

5.3.1 发射天线数与接收天线数相等的情况 (N_t=N_r).

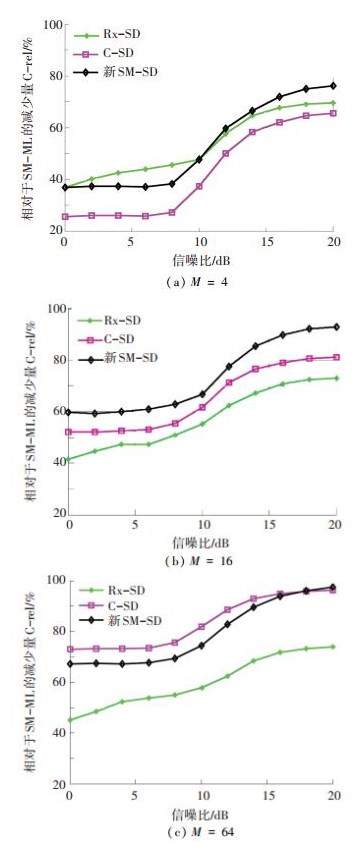
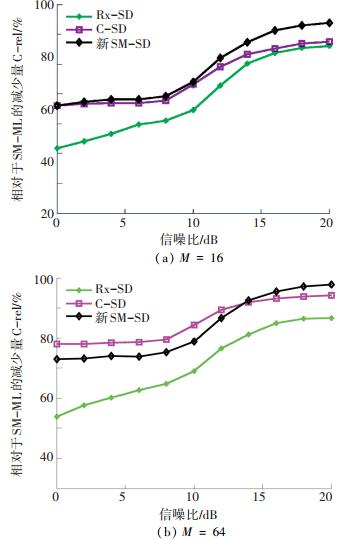
图 6和图 7是在N_t=N_r时几种算法的运算复杂度仿真结果.已知Rx-SD适用于N_r较大的情况，而C-SD适用于发射搜索空间较大的系统，这从图 6中也可以看出. 图 6和图 7表明：新SM-SD同样适用于发射搜索空间大的系统，且优于C-SD，运算复杂度可达到SM-ML的10%以下.不过，随着M的增大，新SM-SD和C-SD的运算复杂度都不断降低，新SM-SD的优势逐渐减小，当M=64时，只有在高信噪比时新SM-SD才优于C-SD.这是因为当M足够大时，预先复杂度处于主导位置，而新SM-SD在实数化预处理时的预先复杂度高于C-SD.此外，图 6也表明：在某些Rx-SD占优的情况下，信噪比较高时，新SM-SD也可以是最优的.

5.3.2 发射天线数与接收天线数不相等的情况 (N_t≠N_r)

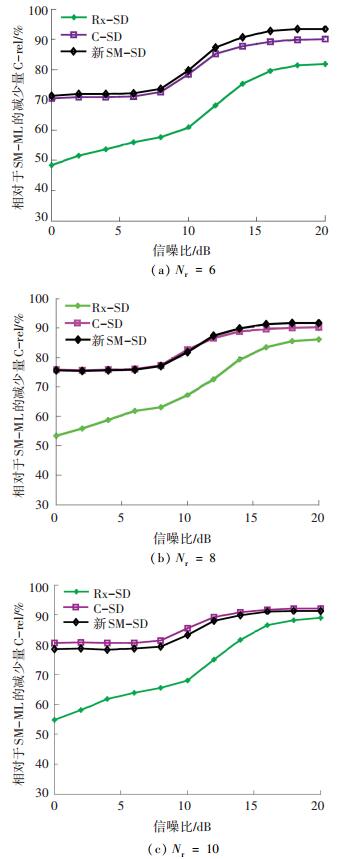
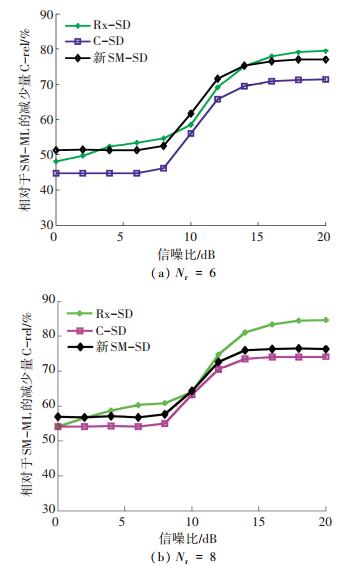
这里只考虑超定系统 (N_r>N_t) 的情况. 图 8和图 9是在N_t≠N_r时几种算法的运算复杂度仿真结果，从两个方面来分析新SM-SD的运算复杂度，图 8和图 9表明：

1) 若“发射搜索空间”不变，当N_r=6和N_r=8时，新SM-SD均优于C-SD，随着N_r增大，Rx-SD的优势逐渐显现，而新SM-SD相对于C-SD的优势减小，这是由于新SM-SD中QR分解的运算复杂度受N_r的影响大.

2) 若“接收搜索空间”不变，当m增加，即频谱效率增加时，新SM-SD和C-SD的运算复杂度会降低，且新SM-SD始终优于C-SD，并在m=6时优于Rx-SD.相比于SM-ML，m=6时的运算复杂度减少效果比m=4时提升了将近20%.因此，新SM-SD算法更加适合于检测空间调制信号.

6 结语

本文提出一种具有新型实数化变换方式的新SM-SD算法，实发射向量中的两维非零元素的位置相邻，且检测时相邻的两层互不影响，降低了运算复杂度.理论上分析了新SM-SD算法的运算复杂度，在不同的SM系统中对新SM-SD算法的误比特性能和运算复杂度进行仿真，并与已有的SM-SD算法相比较.理论分析和仿真结果表明：新SM-SD算法在一定条件下可以降低运算复杂度，同时保持了与ML相同的误比特性能，尤其在多数情况下优于C-SD.在“发射搜索空间”较大，N_r不是很大的情况下，新SM-SD算法降低运算复杂度的效果十分理想，明显优于C-SD和Rx-SD；在某些“接收搜索空间”较大的情况下，高信噪比时新SM-SD也会优于Rx-SD成为最佳选择.