共形阵列[1-5]是由共形载体上共形辐射单元构成的天线阵列.作为共形阵列的典型代表,锥面共形阵列具有利用孔径充分、节省空间、满足空气动力学要求、对极化信息敏感等特点,在电子侦察、电子对抗、航空航天及通信等领域有着广泛的应用前景.
目前对共形阵列的研究主要包括:共形辐射单元设计及辐射特性研究[1-2],共形天线阵列的分析和综合优化[3-5],以及共形阵列参数估计[6-13].在共形阵列参数估计方面,文献[6]考虑共形阵列天线的多极化特性,基于四阶累积量和对阵列结构的设计,结合ESPRIT (estimation of signal parameters via rotational invariance techniques) 算法实现三种 (柱面、锥面、球面) 共形阵列条件下的盲极化DOA估计;文献[7]针对共形阵列流形中DOA与极化参数的“耦合”,利用偶极子阵元在锥面和柱面共形载体上合理布阵,使用ESPRIT算法实现了DOA和极化参数的联合估计;文献[8]将任意基线算法扩展到三维阵列,结合虚拟基线方法,利用子阵分割和矩阵求逆的方法实现了共形阵列条件下的二维DOA估计;文献[9]利用虚拟内插变换将共形阵列转换为虚拟的线性阵列,并结合经典联合迭代自校正算法,实现了阵列误差的自校正以及DOA的估计;文献[10]利用MUSIC算法实现了共形阵列的极化-DOA的联合估计;文献[11]利用柱面共形阵列的对称性,结合ESPRIT实现了DOA和极化参数的估计;文献[12]针对阵元互耦和遮挡效应,通过模式空间变换和秩损理论,实现了柱面共形阵列的DOA估计.在共形阵列参数估计性能分析方面,文献[13]推导了MUSIC算法在共形阵列中的DOA参数估计方差和克拉美-罗界,并通过仿真对比研究了MUSIC算法在面阵和共形阵列中的DOA估计精度.
在共形阵列的参数估计方面已有算法主要分为两类:不同背景下的DOA参数估计[6, 8-9, 12]以及极化和DOA参数的联合估计[7, 10-11].在极化和DOA联合估计算法方面,已有文献主要通过ESPRIT算法和MUSIC算法实现,其中ESPRIT算法对阵列形式有一定限制且需要进行参数配对,MUSIC算法对阵列形式限制较少,但需要进行四维参数搜索,计算复杂度较高.针对以上问题,本文提出一种基于锥面共形阵列的降维MUSIC算法,算法通过构造同极化接收子阵,将导向矢量中的空域信息和极化信息去耦合,结合“秩损”原理实现了极化-DOA估计的降维MUSIC算法,与文献[10]方法相比大大降低了极化-DOA估计算法的计算复杂度,且不需要进行参数配对.
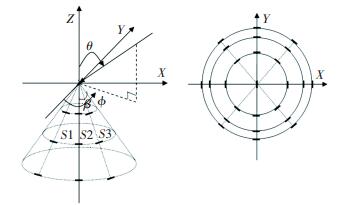
1 锥面共形阵列信号模型 1.1 锥面共形阵列结构锥面共形阵列的结构如图 1所示,阵列由单极化阵元构成,在圆锥顶点处存在一个阵元,其下有若干圆环阵.定义β为1/2圆锥顶角,信号入射方向θ、φ定义如图 1所示,n为由上至下的圆环阵序号,d为圆环阵的间距,过圆锥顶点沿锥面分布的S1、S2、S3等直线定义为锥面的母线,每层圆环阵共含8个阵元,均位于相应的母线上,每层圆环阵中阵元序号m以X正轴为起点,按逆时针方向排列.
|
图 1 锥面共形阵列示意 Figure 1 Conical conformal array structure |
图 1所示的锥面共形阵列,其阵元坐标为
| $ \begin{array}{l} {x_{nm}} = nd \times \tan \beta \times \cos \left[ {2\pi \left( {m - 1} \right)/8} \right],\\ {y_{nm}} = nd \times \tan \beta \times \sin \left[ {2\pi \left( {m - 1} \right)/8} \right],\\ {z_{nm}} = - nd. \end{array} $ |
考虑如图 1所示的锥面共形阵列:圆锥顶点处有1个阵元,其他阵元分布在L条母线上,每条母线有K个阵元,阵元数为N=L×K+1.假设有M个信号入射到锥面共形阵列上,则其接收信号模型可以表示为
| $ \mathit{\boldsymbol{X}}\left( t \right) = \mathit{\boldsymbol{\tilde A}}\left( {\theta ,\varphi ,\gamma ,\eta } \right)\mathit{\boldsymbol{S}}\left( t \right) + \mathit{\boldsymbol{N}}\left( t \right). $ |
式中: X (t) 为阵列接收信号; S (t) 为信号矢量,N (t) 为噪声矢量;
| $ \begin{array}{l} \mathit{\boldsymbol{\tilde A}}\left( {\theta ,\varphi ,\gamma ,\eta } \right) = \left[ {\mathit{\boldsymbol{\tilde a}}\left( {\theta_1 ,\varphi ,\gamma_1 ,\eta_1 } \right), \cdots ,\mathit{\boldsymbol{\tilde a}}\left( {{\theta _M},{\varphi _M},{\gamma _M},{\eta _M}} \right)} \right],\\ \mathit{\boldsymbol{\tilde a}}\left( {{\theta _i},{\varphi _i},{\gamma _i},{\eta _i}} \right) = {\mathit{\boldsymbol{a}}_s}\left( {{\theta _i},{\varphi _i}} \right) \odot {\mathit{\boldsymbol{a}}_p}\left( {{\theta _i},{\varphi _i},{\gamma _i},{\eta _i}} \right), \end{array} $ | (1) |
| $ \begin{array}{l} {\mathit{\boldsymbol{a}}_s}\left( {{\theta _i},{\varphi _i}} \right) = \left[ {1,\exp \left( { - \frac{{2\pi }}{\lambda }{\mathit{\boldsymbol{k}}_i}\mathit{\boldsymbol{l}}{S_{\left( {1,1} \right)}}} \right)},\cdots , \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\exp \left( { - \frac{{2\pi }}{\lambda }{\mathit{\boldsymbol{k}}_i}{\mathit{\boldsymbol{l}}_{S\left( {1,K} \right)}}} \right), \cdots ,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\exp \left( { - \frac{{2\pi }}{\lambda }{\mathit{\boldsymbol{k}}_i}{\mathit{\boldsymbol{l}}_{S\left( {L,1} \right)}}} \right), \cdots ,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left. {\exp \left( { - \frac{{2\pi }}{\lambda }{\mathit{\boldsymbol{k}}_i}{\mathit{\boldsymbol{l}}_{\left( {L,K} \right)}}} \right)} \right]^{\rm{T}}},\\ {\mathit{\boldsymbol{a}}_p}\left( {{\theta _i},{\varphi _i},{\gamma _i},{\eta _i}} \right) = \left[ {{p_0},{p_{S\left( {1,i} \right)}}, \cdots ,{p_{S\left( {1,i} \right)}},{p_{S\left( {2,i} \right)}}, \cdots ,} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left. {{p_{S\left( {2,i} \right)}}, \cdots ,{p_{S\left( {L,i} \right)}}, \cdots ,{p_{S\left( {L,i} \right)}}} \right]^{\rm{T}}}. \end{array} $ |
式中:
由阵列的建模过程可知,阵元受共形阵列曲率影响,使其具有不同的极化状态,但同一条母线上的阵元由于在方向图旋转变换过程中具有相同的欧拉旋转角,因此具有相同的极化状态[10],对入射信号的极化响应相同.本文正是利用同母线阵元的同极化特性实现了极化-DOA估计的降维算法.
2 基于降维MUSIC的极化-DOA联合估计 2.1 锥面共形阵列的MUSIC算法原理定义单极化阵元共形阵列的协方差矩阵为
| $ {\mathit{\boldsymbol{R}}_x} = {\rm{E}}\{ \mathit{\boldsymbol{X}}\left( t \right){\mathit{\boldsymbol{X}}^{\rm{H}}}\left( t \right)\} , $ |
对Rx进行特征值分解有
| $ {\mathit{\boldsymbol{R}}_x} = \mathit{\boldsymbol{U \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{U}}^{\rm{H}}} = \sum\limits_{i = 1}^N {{\lambda _i}{\mathit{\boldsymbol{u}}_i}\mathit{\boldsymbol{u}}_i^{\rm{H}}} . $ |
式中:U = {u1 u2 … }为特征向量矩阵;Λ =diag{λ1, λ2, …, λM, λM+1…, λN}为特征值矩阵,且有λ1≥λ2, ≥…, ≥λM>λM+1=…=λN=σ2.根据子空间原理,可知由特征向量张成的信号子空间和噪声子空间分别为
| $ \begin{array}{l} \left\langle S \right\rangle = {\rm{span}}\{ {\mathit{\boldsymbol{U}}_s}\} = {\rm{span}}\{ {\mathit{\boldsymbol{u}}_1},{\mathit{\boldsymbol{u}}_2}, \cdots {\mathit{\boldsymbol{u}}_M}\} ,\\ \left\langle N \right\rangle = {\rm{span}}\{ \left. {{\mathit{\boldsymbol{U}}_N}} \right)\} = {\rm{span}}\{ {\mathit{\boldsymbol{u}}_{M + 1}}, \cdots {\mathit{\boldsymbol{u}}_N}\} . \end{array} $ |
进一步由子空间原理可知,信号导向矢量与噪声空间正交,即
| $ \mathit{\boldsymbol{\tilde a}}{\left( {{\theta _i},{\varphi _i},{\gamma _i},{\eta _i}} \right)^{\rm{H}}}{\mathit{\boldsymbol{U}}_N} = 0,i = 1,2, \cdots ,M. $ | (2) |
由式 (2) 可定义极化-DOA联合谱表达式为
| $ \mathit{\boldsymbol{P}}\left( {\theta ,\varphi ,\gamma ,\eta } \right) = \frac{1}{{{{\left\| {\mathit{\boldsymbol{\tilde a}}{{\left( {{\theta },{\varphi},{\gamma},{\eta}} \right)}^{\rm{H}}}{\mathit{\boldsymbol{U}}_N}} \right\|}^2}}}. $ | (3) |
对式 (3) 进行四维搜索,得到M个极大值所对应的参数值即为对信号参数 (θ, φ, γ, η) 的估计.由于在参数估计过程中需要进行四维搜索,算法的计算复杂度较高,不利于工程实现.针对此问题,本文从导向矢量中极化信息和DOA信息解耦合的角度出发,通过秩损原理实现了极化-DOA参数估计的降维算法,大大降低了算法的计算复杂度.
2.2 锥面共形阵列的降维MUSIC算法原理由式 (1) 可知,导向矢量可重写为
| $ \begin{array}{l} \mathit{\boldsymbol{\tilde a}}\left( {\theta ,\varphi ,\gamma ,\eta } \right) = {\mathit{\boldsymbol{a}}_s}\left( {\theta ,\varphi } \right) \odot {\mathit{\boldsymbol{a}}_p}\left( {\theta ,\varphi ,\gamma ,\eta } \right) = \\ \left[ \begin{array}{l} 1\\ \exp \left( { - \frac{{2\pi }}{\lambda }\mathit{\boldsymbol{k}} \cdot {\mathit{\boldsymbol{l}}_{S\left( {1,1} \right)}}} \right)\\ \vdots \\ \exp \left( { - \frac{{2\pi }}{\lambda }\mathit{\boldsymbol{k}} \cdot {\mathit{\boldsymbol{l}}_{S\left( {1,K} \right)}}} \right)\\ \vdots \\ \exp \left( { - \frac{{2\pi }}{\lambda }\mathit{\boldsymbol{k}} \cdot {\mathit{\boldsymbol{l}}_{S\left( {L,1} \right)}}} \right)\\ \vdots \\ \exp \left( { - \frac{{2\pi }}{\lambda }\mathit{\boldsymbol{k}} \cdot {\mathit{\boldsymbol{l}}_{\left( {L,K} \right)}}} \right) \end{array} \right] \cdot \left[ \begin{array}{l} {p_0}\\ {p_{S\left( 1 \right)}}\\ \vdots \\ {p_{S\left( 1 \right)}}\\ \vdots \\ {p_{S\left( L \right)}}\\ \vdots \\ {p_{S\left( L \right)}} \end{array} \right] = \\ \left[ {\begin{array}{*{20}{c}} 1 & 0 & 0 & 0 & 0\\ {\bf{0}} & {{\mathit{\boldsymbol{a}}_{s1}}\left( {\theta ,\varphi } \right)} & {\bf{0}} & {\bf{0}} & {\bf{0}}\\ {\bf{0}} & {\bf{0}} & {{\mathit{\boldsymbol{a}}_{s2}}\left( {\theta ,\varphi } \right)} & {\bf{0}} & {\bf{0}}\\ {\bf{0}} & {\bf{0}} & {\bf{0}} & \ddots & {\bf{0}}\\ {\bf{0}} & {\bf{0}} & {\bf{0}} & {\bf{0}} & {{\mathit{\boldsymbol{a}}_{sL}}\left( {\theta ,\varphi } \right)} \end{array}} \right]\left[ \begin{array}{l} {p_0}\\ {p_{S\left( 1 \right)}}\\ \vdots \\ {p_{S\left( L \right)}} \end{array} \right] \buildrel \Delta \over = \\ {\mathit{\boldsymbol{a}}_\sum }\left( {\theta ,\varphi ,\gamma ,\eta } \right) \times {\mathit{\boldsymbol{a}}_L}\left( {\theta ,\varphi ,\gamma ,\eta } \right), \end{array} $ | (4) |
其中
| $ {\mathit{\boldsymbol{a}}_L}\left( {\theta ,\varphi ,\gamma ,\eta } \right) = {\left[ {\begin{array}{*{20}{c}} {{p_0}} & {{p_{S\left( 1 \right)}}} & \cdots & {{p_{S\left( L \right)}}} \end{array}} \right]^{\rm{T}}}, $ | (5) |
| $ {\mathit{\boldsymbol{a}}_\sum }\left( {\theta ,\varphi } \right) = \left[ {\begin{array}{*{20}{c}} 1 & 0 & 0 & 0 & 0\\ {\bf{0}} & {{\mathit{\boldsymbol{a}}_{s1}}\left( {\theta ,\varphi } \right)} & {\bf{0}} & {\bf{0}} & {\bf{0}}\\ {\bf{0}} & {\bf{0}} & {{\mathit{\boldsymbol{a}}_{s2}}\left( {\theta ,\varphi } \right)} & {\bf{0}} & {\bf{0}}\\ {\bf{0}} & {\bf{0}} & {\bf{0}} & \ddots & {\bf{0}}\\ {\bf{0}} & {\bf{0}} & {\bf{0}} & {\bf{0}} & {{\mathit{\boldsymbol{a}}_{sL}}\left( {\theta ,\varphi } \right)} \end{array}} \right]. $ |
asl(θ, φ)(l=1, 2, …, L) 为第l条母线阵元空域信息的导向矢量,可表示为
| $ {\mathit{\boldsymbol{a}}_{sl}}\left( {\theta ,\varphi } \right) = {\left[ {\begin{array}{*{20}{c}} {\exp \left( { - \frac{{2\pi }}{\lambda }\mathit{\boldsymbol{k}} \cdot {\mathit{\boldsymbol{l}}_{S\left( 1 \right)}}} \right)} & \cdots & {\exp \left( { - \frac{{2\pi }}{\lambda }\mathit{\boldsymbol{k}} \cdot {\mathit{\boldsymbol{l}}_{S\left( K \right)}}} \right)} \end{array}} \right]^{\rm{T}}}, $ |
由子空间原理知,导向矢量参数与入射信号参数匹配时,有
| $ \begin{array}{l} {\left\| {\mathit{\boldsymbol{\tilde a}}{{\left( {{\theta _i},{\varphi _i},{\gamma _i},{\eta _i}} \right)}^{\rm{H}}}{\mathit{\boldsymbol{U}}_N}} \right\|^2} = \mathit{\boldsymbol{\tilde a}}{\left( {{\theta _i},{\varphi _i},{\gamma _i},{\eta _i}} \right)^{\rm{H}}}{\mathit{\boldsymbol{U}}_N}\mathit{\boldsymbol{U}}_N^{\rm{H}}\mathit{\boldsymbol{\tilde a}}\left( {{\theta _i},} \right.\\ \;\;\;\;\;\left. {{\varphi _i},{\gamma _i},{\eta _i}} \right) = 0,i = 1,2, \cdots ,M. \end{array} $ | (6) |
将式 (4) 代入到式 (6) 中,整理可得
| $ \begin{array}{l} \mathit{\boldsymbol{a}}_L^{\rm{H}}\left( {{\theta _i},{\varphi _i},{\gamma _i},{\eta _i}} \right) \times \mathit{\boldsymbol{a}}_\sum ^{\rm{H}}\left( {{\theta _i},{\varphi _i}} \right) \times {\mathit{\boldsymbol{U}}_N}\mathit{\boldsymbol{U}}_N^{\rm{H}} \times \\ \;\;\;\mathit{\boldsymbol{a}}_\sum \left( {{\theta _i},{\varphi _i}} \right) \times {\mathit{\boldsymbol{a}}_L}\left( {{\theta _i},{\varphi _i},{\gamma _i},{\eta _i}} \right) = 0,\\ \mathit{\boldsymbol{a}}_L^{\rm{H}}\left( {{\theta _i},{\varphi _i},{\gamma _i},{\eta _i}} \right)\mathit{\boldsymbol{Q}}\left( {{\theta _i},{\varphi _i}} \right){\mathit{\boldsymbol{a}}_L}\left( {{\theta _i},{\varphi _i},{\gamma _i},{\eta _i}} \right) = 0,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1,2, \cdots ,M, \end{array} $ | (7) |
其中
| $ \mathit{\boldsymbol{Q}}\left( {{\theta _i},{\varphi _i}} \right) = a_\sum ^{\rm{H}}\left( {{\theta _i},{\varphi _i}} \right) \times {\mathit{\boldsymbol{U}}_N}\mathit{\boldsymbol{U}}_N^{\rm{H}} \times {\mathit{\boldsymbol{a}}_\sum }\left( {{\theta _i},{\varphi _i}} \right). $ | (8) |
由式 (8) 显然有Q (θi, φi)= QH(θi, φi),此时式 (7) 的左端为矩阵Q (θi, φi) 的二次型表示.由式 (5) 可知,aL(θi, φi, γi, ηi) 为各条母线阵元对入射信号的极化响应,由于各母线间阵元的极化形式不同,因此在L条母线中最多只有1条母线阵元的极化状态与入射信号极化正交,即aL(θi, φi, γi, ηi) 中元素不全为零,aL(θi, φi, γi, ηi) 非零向量,aL(θi, φi, γi, ηi)≠ 0.
当参数 (θ, φ, γ, η)=(θi, φi, γi, ηi), i=1, 2, …, M时,有
当参数 (θ, φ, γ, η)≠(θi, φi, γi, ηi), i=1, 2, …, M时,有
由以上讨论可知,Q (θ, φ) 为半正定矩阵,当且仅当 (θ, φ)=(θi, φi), i=1, 2, …, M时,Q (θ, φ) 为奇异矩阵.即Q (θ, φ) 在信源的真实入射方向 (θi, φi) 处奇异,此时对矩阵Q (θ, φ) 有
| $ \det \left[ {\mathit{\boldsymbol{Q}}\left( {{\theta _i},{\varphi _i}} \right)} \right] = 0,i = 1,2, \cdots ,M. $ |
需要注意的是,由于共形载体对阵元的遮挡效应,使得a Σ(θi, φi) 的对角线存在部分元素为0的现象[10],在这种情况下,即使 (θ, φ) 与信号的真实入射方向不对应,也会使矩阵Q奇异.因此需要对由阵列遮挡效应造成矩阵Q的奇异性进行处理.由文献[10]中讨论可知,在有遮挡效应的情况下,未受遮挡阵元对应的导向矢量仍然与噪声空间中相应的元素正交.因此在按照式 (8) 构造Q后,将Q中全为0的行和列去掉得到Q′阵,此时对Q′阵有
| $ \det \left[ {\mathit{\boldsymbol{Q'}}\left( {{\theta _i},{\varphi _i}} \right)} \right] = 0,i = 1,2, \cdots ,M. $ |
根据矩阵行列式与矩阵特征值关系,可得对入射信源的二维DOA估计为
| $ \left( {\hat \theta ,\hat \varphi } \right) = \arg \mathop {\min }\limits_{\left( {\theta ,\varphi } \right)} \left\{ {\frac{1}{{{\lambda _{\min }}\left\{ {\mathit{\boldsymbol{Q'}}\left( {\theta ,\varphi } \right)} \right\}}}} \right\}, $ | (9) |
式中,λmin{·}表示矩阵的最小特征值.
由式 (9) 得到多个入射信号的DOA参数估计值 (
| $ \mathit{\boldsymbol{P}}\left( {\hat \theta ,\hat \varphi ,\gamma ,\eta } \right) = \frac{1}{{{{\left\| {\mathit{\boldsymbol{\tilde a}}{{\left( {\hat \theta ,\hat \varphi ,\gamma ,\eta } \right)}^{\rm{H}}}{\mathit{\boldsymbol{U}}_N}} \right\|}^2}}}. $ | (10) |
对式 (10) 分别作极化参数的二维估计,可得与DOA参数相对应的极化参数估计结果.
降维MUSIC算法步骤:
1) 计算阵列协方差矩阵,并作特征值分解,得到噪声子空间UN;
2) 根据式 (8) 构造矩阵Q,并去掉其中全为零的行和列,得到Q′阵;
3) 根据式 (9) 进行角度域的二维搜索,得到DOA参数的估计;
4) 将DOA估计值代入到式 (10) 中,在极化域进行二维搜索,得到极化参数估计.
综上,通过对导向矢量中极化信息和DOA信息的剥离,算法实现了参数估计的降维处理,先由式 (9) 估计信号的DOA参数,然后通过式 (10) 估计信号的极化参数.可以看出降维算法将传统MUSIC算法所需的四维参数搜索转化为2个二维参数搜索,大大降低了计算复杂度;同时在参数估计过程中实现了估计参数的自动配对,避免了ESPRIT算法所需的参数配对问题.
2.3 降维算法计算复杂度分析在计算复杂度方面,降维MUSIC算法与传统MUSIC算法的计算量均可分为阵列协方差矩阵计算、特征值分解和谱函数计算三部分.为方便比较,假设两种算法对应的导向矢量通过正余弦查表得到,暂不考虑其计算量;与计算量有关的参数为阵元个数N、入射的信号源个数M、母线个数L、快拍数P;不失一般性,假设极化和DOA参数的搜索范围为各自的值域范围,即θ为0°~90°,φ为0°~360°,γ为0°~90°,η为0°~360°,各参数的搜索步长均为1°.
2.3.1 阵列协方差矩阵计算两个复数相乘的计算量为 (4m+2a)(m表示乘法,a表示加法,下同),因此其单快拍自相关矩阵的计算量为N×N×(4m+2a),对P个快拍,阵列自相关矩阵的计算量为P×N2×(4m+2a)+P×N2×2a.两种算法均是对N个阵元的协方差矩阵进行计算,因此本部分的计算量二者相同.
2.3.2 特征值分解在特征子空间计算过程中,两种算法均需要对N维阵列协方差矩阵Rxx进行特征值分解,因此在本部分二者的计算量相同.由文献[14]知,采用Lanczos算法计算N维矩阵的特征子空间分解时,其计算量主要为N3次的复数乘法,即文中阵列协方差矩阵特征分解的计算量为N3×(4m+2a).
2.3.3 谱函数计算谱函数部分的计算量由需要计算的谱函数点数和每点所需的计算量确定.
传统MUSIC:算法需要完成1次四维参数搜索,所需计算的谱函数点数为90×360×90×360,每个函数点涉及的计算为导向矢量与噪声子空间相乘得到的行向量au以及计算au的模.计算au所需的计算量为[N×(4m+2a)+N×2a]×(N-M),计算向量au的模需要的计算量为 (N-M)×(4m+2a)+(N-M)×2a,整理后得传统MUSIC所需计算量为90×360×90×360×[(N-M)×(N+1)×(4m+4a)].
降维MUSIC:算法需要完成1次二维DOA搜索,以及M次二维极化参数搜索.
1) DOA搜索所需的谱函数点数为90×360,每个函数点需要的计算为:矩阵Q的构造以及矩阵Q的特征值分解,其中计算矩阵Q所需的计算量为 (L+1)×(N-M)×N×(4m+4a)+(L+1)3×(4m+2a),矩阵Q的特征值分解所需的计算量为 (L+1)3×(4m+2a).整理后可得降维算法计算二维DOA搜索需要的计算量为
| $ \begin{array}{l} 90 \times 360 \times \left\{ {\left[ {\left( {L + 1} \right) \times \left( {N - M} \right) \times N + } \right.} \right.\\ \left. {\left. {{{\left( {L + 1} \right)}^3}} \right] \times \left( {4m + 4a} \right) + {{\left( {L + 1} \right)}^3} \times \left( {4m + 2a} \right)} \right\}. \end{array} $ |
2) 极化参数搜索需要进行M次二维极化参数计算,需要计算的谱函数点数为M× 90×360,每个谱函数点所需的计算量与传统MUSIC相同,为[(N-M)×(N+1)×(4m+4a)],因此可得极化参数搜索需要的计算量为M×90×360×[(N-M)×(N+1)×(4m+4a)].
整理可得降维MUSIC算法所需的计算量为
| $ \begin{array}{l} 90 \times 360 \times \left\{ {\left[ {\left( {L + 1} \right) \times \left( {N - M} \right) \times N + \left( {L + } \right.} \right.} \right.\\ \left. {\left. {{{\left. 1 \right)}^3}} \right] \times \left( {4m + 4a} \right) + {{\left( {L + 1} \right)}^3} \times \left( {4m + 2a} \right)} \right\} + \\ M \times 90 \times 360 \times \left[ {\left( {N - M} \right) \times \left( {N + 1} \right) \times } \right.\\ \left. {\left( {4m + 4a} \right)} \right]. \end{array} $ |
由于目前的数字信号处理芯片一般具有独立的加法和乘法运算单元,可认为乘法和加法占用的指令周期相同.若取阵元个数N= 25,入射的信号源个数M= 2,母线个数L= 6,快拍数P= 500,传统MUSIC算法和降维MUSIC算法所需的计算量对比如表 1所示.
| 表 1 传统MUSIC算法和降维MUSIC算法计算量比较 (乘加次数) Table 1 Compute complexity comparison between MUSIC and dimension reduced MUSIC (multiplicatio times) |
由表 1可以看出,传统算法与降维算法在阵列协方差矩阵计算和特征值分解部分的计算量相同,在多维参数搜索过程中,由于降维算法将四维的遍历搜索过程改进为二维DOA与二维极化参数的搜索计算,因此降低了极化-DOA估计算法的计算量,二种算法在参数搜索部分的计算量之比约为3 121:1.
3 仿真实验本节通过Matlab仿真研究降维MUSIC算法的有效性以及参数估计精度.仿真中所取锥面共形阵列形式如图 1所示,具体参数为:β= 20°,圆锥顶点处布有一个阵元,其下共有4个圆环阵,每个圆环阵有6个阵元,均匀分布在圆环上,圆环阵之间距离为2.75λ.
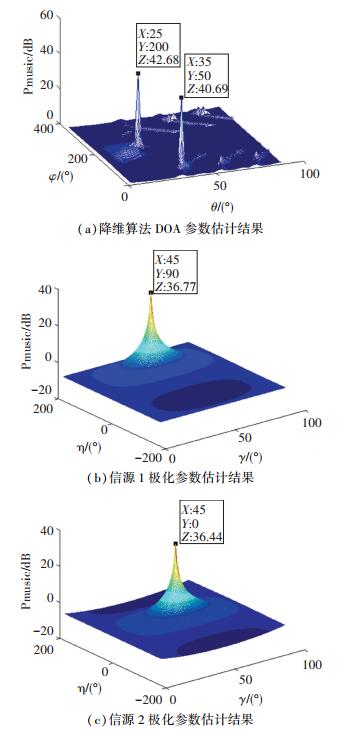
3.1 降维MUSIC算法有效性验证仿真条件:信噪比20 dB,快拍数500,取极化和DOA参数均不同的两个信源,参数分别为 (θ1, φ1, γ1, η1)=(25°, 200°, 45°, 90°),(θ2, φ2, γ2, η2)=(35°, 50°, 45°, 0°),降维MUSIC算法所得仿真结果如图 2所示.
|
图 2 降维MUSIC算法参数估结果 Figure 2 Parameter estimation figure of dimension reduced MUSIC |
由图 2(a)可以看出,虽然两个入射信源的极化参数不同,但降维MUSIC算法通过在二维DOA域的搜索实现了对2个信源DOA参数的估计,避免了传统MUSIC算法所需的四维搜索,大大降低了参数估计算法的计算复杂度.由图 2(b)、(c)可以看出,在得到信源DOA参数估计结果后,将其分别代入到式 (10) 给出的极化参数谱估计表达式中,即可分别得到与DOA参数相匹配的极化参数估计结果. 图 2所示的仿真结果证明了降维MUSIC算法实现极化-DOA参数估计的有效性.
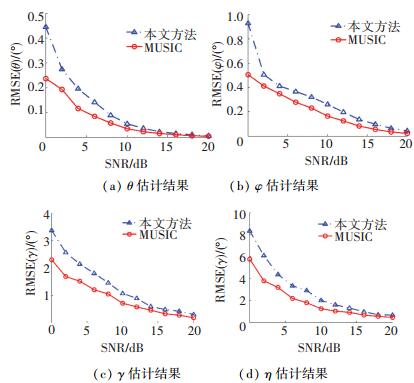
3.2 降维MUSIC算法参数估计精度仿真仿真条件:阵列接收快拍数500,单信源入射,参数为 (θ1, φ1, γ1, η1)=(15°, 200°, 45°, 100°),信噪比从0 dB变化到20 dB,蒙特卡洛实验次数500,统计算法参数估计的均方根误差,仿真结果如图 3所示.
|
图 3 降维MUSIC算法参数估计精度仿真 Figure 3 Parameter estimation precision of dimension reduced MUSIC |
由图 3所示的仿真结果可以看出,本文方法对DOA参数和极化参数的估计精度略逊于MUSIC算法,在信噪比低于10 dB时,两种算法的参数估计精度相差较大.随着信噪比的逐渐增加,本文方法与MUSIC算法的估计精度差逐渐变小.
综合仿真实验1和2的结果,以及2.3节计算量的讨论可以看出,降维算法在牺牲部分精度的前提下,有效降低了极化-DOA联合估计算法的计算量. MUSIC算法四维空间搜索所需计算量巨大,不利于工程实现; 若在实际工程应用中,允许对锥面共形阵列构造同极化接收子阵,则降维算法可有效降低计算复杂度,有利于工程的实现.
4 结论在建立单极化阵元锥面共形阵列信号模型的基础上,通过构造同极化接收子阵,完成了空域信息和极化域信息的去耦合,根据秩损原理实现了极化-DOA估计的降维MUSIC算法,并通过仿真实验研究了降维算法的估计精度.仿真结果表明,本文方法可以有效实现极化-DOA参数的降维估计,大大降低了联合估计算法的计算量,为共形阵列在工程上的应用提供了一个可选择的方案.同时,也可以看到本文方法在参数估计精度的仿真结果逊色于MUSIC算法,另外降维MUSIC算法参数估计精度的理论分析也尚未进行,相信随着更多同行的研究,以上问题将最终得到解决.
| [1] | HUANG Q, ZHOU H, BAO J, et al. Accurate calibration of mutual coupling for conformal antenna arrays[J]. Electronics Letters, 2013, 49(23): 1418-1420. DOI: 10.1049/el.2013.2258 |
| [2] | RASEKH M, SEYDNEJAD S R. Design of an adaptive wideband beamforming algorithm for conformal arrays[J]. IEEE Communications Letters, 2014, 18(11): 1955-1958. DOI: 10.1109/LCOMM.2014.2357417 |
| [3] | HUANG Zhijiang, ZHOU Jie, ZHANG Haiping. Full polarimetric sum and difference patterns synthesis for conformal array[J]. Electronics Letters, 2015, 51(8): 602-604. DOI: 10.1049/el.2014.4428 |
| [4] | LI Yongjiu, LI Long. Broadband microstrip beam deflector based on dual-resonance conformal loops array[J]. IEEE Transactions on Antennas and Propagation, 2014, 62(6): 3028-3034. DOI: 10.1109/TAP.2014.2314741 |
| [5] | XU Kuiwen, YE Dexin, ZHU Zhongbo, et al. Analytical beam forming for circularly symmetric conformal apertures[J]. IEEE Transactions on Antennas and Propagation, 2015, 63(4): 1458-1464. DOI: 10.1109/TAP.2014.2382663 |
| [6] | QI Z S, GUO Y, WANG B H. Blind direction of arrival estimation angorithm for conformal array antenna with respect to polarization diversity[J]. IET Microwaves, Antennas & Propagation, 2011, 5(4): 433-442. |
| [7] |
张树银, 郭英, 齐子森, 等. 基于子空间原理的共形阵列多参数联合估计算法[J].
系统工程与电子技术, 2012, 34(6): 1146-1152.
ZHANG Shuyin, GUO Ying, QI Zisen, et al. Subspace-based multiple parameter estimation algorithm for incident signals with conformal array[J]. Systems Engineering and Electronic, 2012, 34(6): 1146-1152. |
| [8] |
司伟建, 万良田, 刘鲁涛, 等. 共形阵列天线超宽频带波达方向实时估计[J].
哈尔滨工程大学学报, 2014, 35(7): 913-918.
SI Weijian, WAN Liangtian, LIU Lutao, et al. Real-time ultra-wideband direction finding for the conformal array antenna[J]. Journal of Harbin Engineering University, 2014, 35(7): 913-918. |
| [9] |
张学敬, 杨志伟, 廖桂生. 共形阵列幅相误差校正快速算法[J].
电子与信息学报, 2014, 36(5): 1100-1105.
ZHANG Xuejing, YANG Zhiwei, LIAO Guisheng. A fast method for gain-phase error calibration in conformal array[J]. Journal of Electronics & Information Technology, 2014, 36(5): 1100-1105. |
| [10] |
刘帅, 周洪娟, 金铭, 等. 锥面共形阵列天线的极化-DOA估计[J].
系统工程与电子技术, 2012, 33(2): 253-257.
LIU S, ZHOU H J, JIN M, et al. Polarization-DOA estimation for conical conformal array antennas[J]. Systems Engineering and Electronics, 2012, 33(2): 253-257. |
| [11] | ZOU L, LASENBY J, HE Z. Direction and polarisation estimation using polarised cylindrical conformal arrays[J]. IET Signal Processing, 2012, 6(5): 395-403. DOI: 10.1049/iet-spr.2011.0287 |
| [12] | YANG Kai, ZHAO Zhiqin, YANG Wei, et al. Direction of arrival estimation on cylindrical conformal array using RARE[J]. Journal of Systems Engineering and Electronics, 2011, 22(5): 767-772. DOI: 10.3969/j.issn.1004-4132.2011.05.007 |
| [13] |
齐子森, 郭英, 王布宏, 等. 共形阵列天线MUSIC算法性能分析[J].
电子与信息学报, 2008, 30(11): 2674-2677.
QI Zisen, GUO Ying, WANG Buhong, et al. Performance analysis of MUSIC for conformal array[J]. Journal of Electronics & Information Technology, 2008, 30(11): 2674-2677. |
| [14] | XU G, KAILATH T. A Fast Algorithm for Signal Subspace Decomposition and Its Performance Analysis[C]//International Conference on Acoustics, Speech, and Signal Processing.Toronto: IEEE, 1991:3069-3072. |
 2017, Vol. 49
2017, Vol. 49


