低密度奇偶校验^[1](low density parity check, LDPC) 码是一类具有稀疏奇偶校验矩阵的分组纠错码.在过去二十年中，由于LDPC码通过消息传递算法进行解码时，拥有接近理论极限速率的卓越性能^[2]，在实际应用中得到了广泛关注.

无线网络中的协同通信能够改进发射分集和频谱效率^[3], 而中继节点的合理设计能够极大地增强系统的性能.流行的中继协议有放大转发^[4](amplify and forward, AF) 和解码转发^[5](decode and forward, DF).然而，AF中不能进行噪声抑制，在较差信道的条件下会遇到严重的噪声传播和功率下降问题.虽然DF协议允许重新生成所发送的信号，避免了噪声传播问题, 但是再生信号中的任何解码错误都可能导致目的节点性能的衰减.软信息中继^[6](soft information relaying, SIR) 协议具有较大的发展前景^[7]，文献[8]提出一种直接转矩控制方案，将SIR结合分布式Turbo编码.文献[9]提出一个用于所有信道的“软衰减”模型.

由于LDPC码在点对点通信中的性能优越，因此可以将LDPC码应用于中继方案.已经有很多研究者对LDPC码及其改进形式进行了研究，如卷积LDPC编码^[10]的性能优于经典的LDPC分组码，而正交空间耦合的低密度奇偶校验^[11](spatially coupled low density parity check, SC-LDPC) 码被证明可以逼近二元删除信道 (binary erasure channel, BEC)^[12]编码.通过BEC连接，文献[11]将SC-LDPC码用在包括一个中继节点和一个目的节点的网络解码转发方案中，同时证明了通过密度演化，基于SC-LDPC码的方案可以达到理论上的性能极限.因此，SC-LDPC编码可以被视作在中继方案中的极佳编码方式.

本文提出一种基于SC-LDPC码的软信息中继方案，可用于双向中继的加性高斯白噪声信道和瑞利衰落信道.通过在目的节点使用一个估计查找表，提出一个更具现实意义的软噪声近似模型，同时在目的节点处使用方差修正因子 (即方差系数) 以提高高斯近似的准确度.

1 编码设计 1.1 分组码

准循环低密度奇偶校验^[13](quasi cycle low density parity check, QC-LDPC) 矩阵编码在使用滑动窗口消息传递算法进行解码时，其解码性能优于经典的LDPC分组码.由于可以成功地对一小部分码字进行解码，而不用等剩余部分码字都解码完毕，所以使用滑动窗口允许较低的延迟.同时，如果解码窗口大小选择合理，滑动窗口解码器的误差与标准消息传递解码器相似.因此，使用滑动窗口解码器的QC-LDPC码是一个很好的选择.本文考虑基于阵列的QC-LDPC码.

基于阵列 (准循环) 码C_{γ, p}是一个正则LDPC码，由一个γp×p²的奇偶校验矩阵H_{γ, p}定义，其中1≤γ≤p是一个奇素数，具体如下：

$ {\mathit{\boldsymbol{H}}_{\gamma ,p}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{I}} & \mathit{\boldsymbol{I}} & \mathit{\boldsymbol{I}} & \cdots & \mathit{\boldsymbol{I}}\\ \mathit{\boldsymbol{I}} & \sigma & {{\mathit{\boldsymbol{\sigma }}^2}} & \cdots & {{\mathit{\boldsymbol{\sigma }}^{\left( {p - 1} \right)}}}\\ \mathit{\boldsymbol{I}} & {{\sigma ^2}} & {{\mathit{\boldsymbol{\sigma }}^4}} & \cdots & {{\mathit{\boldsymbol{\sigma }}^{2\left( {p - 1} \right)}}}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \mathit{\boldsymbol{I}} & {{\sigma ^{\left( {\gamma - 1} \right)}}} & {{\mathit{\boldsymbol{\sigma }}^{\left( {\gamma - 1} \right)2}}} & {} & {{\mathit{\boldsymbol{\sigma }}^{\left( {\gamma - 1} \right)\left( {p - 1} \right)}}} \end{array}} \right]. $

式中，I表示p×p的单位矩阵，σ为p×p的置换矩阵，其形式为

$ \mathit{\boldsymbol{\sigma = }}\left[ {\begin{array}{*{20}{c}} 0 & 0 & \cdots & 0 & 1\\ 1 & 0 & \cdots & 0 & 0\\ 0 & 1 & \cdots & 0 & 0\\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 1 & 0 \end{array}} \right]. $

另外，通过使用展开程序^[14]得出SC-LDPC分组码.首先，将奇偶校验矩阵切割成两个γp×p²的矩阵，H_u和H_l.切割方式由一个整数向量δ =(δ₀, δ₁, δ₂, …, δ_γ-1) 定义，其中0≤δ₀≤δ₁≤…≤δ_γ-1≤p.

对于所有0≤i≤γ-1，矩阵H_l的i+1行中包含δ_i，与矩阵H_{γ, p}的i+1行的第一个元素相同. H_l中其余的元素被设为0；对于所有0≤i≤γ-1，矩阵H_u的i+1行中包含γp-δ_i，与矩阵H_{γ, p}的i+1行的最后一个元素相同. H_u中其余的元素被设为0.

值得一提的是，对δ的最优选择并不容易.本文对不同分割向量δ进行测试，其结果如表 1所示.通过对误码率 (bit error rate, BER) 性能的研究，对于给定参数γ, k, p和L，选择δ=(5, 4, 2) 时，与加性高斯白噪声和瑞利衰落信道相比，能够提供较优性能.

1.2 信道-网络-编码协同方案

在每个时隙中，目的节点 (信源i) 接收一个信号，在上行链路传输中会有一个来自反向信源i的信号，另一个信号来自下行链接传输.在中继节点无误差解码的情况下，中继节点的转发数据包被视为网络解码序列的信道编码中产生的冗余.因此，信道-网络-编码协同可视为一个网络编码分布LDPC编码方案.

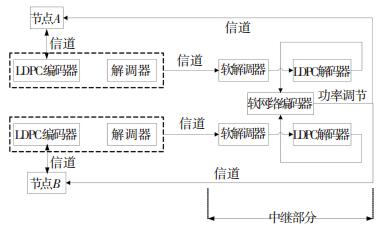
分布式编码方案依赖于对于中继节点处的无误差解码的假设.因此，如果中继节点出现了解码误差，中继节点转发的码字c_R在目的节点处将会是一个错误的网络编码信息序列.如果中继-目的节点链路比直接链路更可靠 (在大部分情况下如此)，那么极有可能目的节点的总体解码将会受到错误中继码字的影响，并由此可能导致解码的失败 (即误码扩散).提出的中继方案如图 1所示，为了缓解中继节点的错误解码造成的误码扩散影响，应用软信息中继，其核心部分为图中的中继部分.通过建立联合网络和信道解码，以增加从中继组件得到的码字作为冗余相关信源的收益.

1.3 软信息中继方案

SIR要求的第一步是对于每个用户i，使用LDPC解码器计算后验LLR.

$ {\lambda _{iR}}\left( {x_i^j\left| {{y_{iR}}} \right.} \right) = \left[ {\log \frac{{P\left( {x_i^j = + 1\left| {{y_{iR}}} \right.} \right)}}{{\left( {x_i^j = - 1\left| {{y_{iR}}} \right.} \right)}}} \right]. $

首先，基于每个用户i接收到的信号帧y_iR，使用一个LDPC解码器可以轻松完成该计算.然后，中继对相应的软网络编码符号进行计算，网络编码操作可以在软域中通过计算后验LLR值获得，公式如下：

$ \tilde x_R^j = \left( {\tanh \left( {\lambda _{AR}^j/2} \right)\tanh \left( {\lambda _{BR}^j/2} \right)} \right). $

式中，$ |\tilde x_R^j| < 1 $，同样$ |\tilde x_{AR}^j| $, $ |\tilde x_{BR}^j| < 1 $.当信噪比较大时，软符号在区域的周边接近-1和+1.然而，由于在信源-中继信道中的严重衰减和低信噪比，软符号的功率可能会非常小，甚至可以忽略不计.因此，网络编码符号总是满足$ |\tilde x_R^j| < \min \{ |\tilde x_{AR}^j|, |\tilde x_{BR}^j|\} $.由于功率很小，且易受噪声影响, 因此本文提出以下网络编码，以提高网络编码符号$ \tilde x_R^j $的可靠性：

$ \begin{array}{l} \tilde x_R^j = {\rm{sign}}\left( {\tanh \left( {\frac{{{\lambda _{ARj}}}}{2}} \right)\tanh \left( {\frac{{{\lambda _{BR,j}}}}{2}} \right)} \right)\\ \;\;\;\;\;\;\;\;\max \left\{ {\left| {\tanh \left( {\frac{{{\lambda _{ARj}}}}{2}} \right)} \right|,\left| {\tanh \left( {\frac{{{\lambda _{ARj}}}}{2}} \right)} \right|} \right\}. \end{array} $

(1)

式 (1) 所表达的意思是：由于$ \tilde x_R^j $是从$ \tilde x_A^j $和$ \tilde x_B^j $中对x_A^jx_B^j的估计，其符号函数应与$ \tilde x_A^j\tilde x_B^j $的符号函数相等, 且信号的幅度并没有显著变化.

最后，从中继发送的信号可被写为$ {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over x} }_R} = \beta {{\tilde x}_R} $，其中因子β为了满足在中继的发送功率约束而选择，即$ E\left( {{{\left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over x} _R^j} \right)}^2}} \right) = 1 $.因此，在信源i处的第三个时隙中的接收信号可被写为

$ {\mathit{\boldsymbol{y}}_{Ri}} = \sqrt {{P_R}} {h_{Ri}}\beta {{\tilde x}_R} + {\mathit{\boldsymbol{n}}_{Ri}}. $

式中，n_Ri为独立同分布的高斯项向量，每项均值为零，方差σ_Ri²=N₀/2.

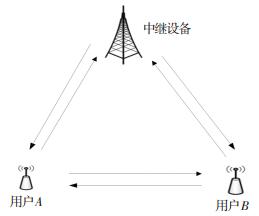
2 目的节点处的LLR计算

一般来说，当LDPC编码与中继结合使用时，在目的节点处对应于中继传输形成的LLR是非常有意义的.半双工模式的双向中继系统如图 2所示.信源A在第2个和第3个时隙中通过两个独立的衰减路径接受到两个不同的信号，即y_BA和y_RA.与之相似，信源B在第一个和第3个时隙中分别接收到y_AB和y_RB两个信号.

本文模型表示正确符号x_R^j=x_A^jx_B^j和软符号$ \tilde x_R^j $之间的关系为

$ \tilde x_R^j = \eta x_R^j + {{\tilde n}^j}. $

(2)

式中，${{\tilde n}^j} $为软误差变量，常数η为软标量.本文计算能够最小化软误差的均方值η值，即η=($ {x_R}{{\tilde x}_R} $).一般来说，软标量可能会被离线计算，对于任何期望的信源-中继信噪比，$ \eta = \frac{1}{N}\sum\limits_{i = 1}^N {\left[{{x_{R, }}_i{{\tilde x}_{R, i}}} \right]} $.本文确定了参数η的一些属性如下：

1) 软标量的值为-1≤η≤1.若信源-中继的信噪比数值较高，$ \tilde x_R^j $≈1，由此可得$ \tilde x_R^j $≈x_R^j≈1.在这种情况下η=1.在$ \tilde x_R^j $出现硬判决错误的情况下，$ \tilde x_R^j $≈x_R^j≈-1.在这种情况下，η=-1.

2) 在η=0时中继不会进行转发. η=0出现在信源-中继信道的低信噪比区域.在此区域中，后验LLR的数量将会非常小.该情况与中继不发送任何信号的情况相似，即中继保持安静.

η产生的效果与衰减系数相似.将此模型应用到网络编码符号中，而不是应用到“软调整”符号中 (该方法的一个优势在于和现有的其他方法相比较，软符号可能具有更高的振幅.这是网络编码操作的收益之一).尝试对软误差方差进行计算.当$ \sigma _{\tilde n}^2 = (\sigma _{{{\tilde x}_R}}^2-{\eta ^2})$时，其中$ \sigma _{{{\tilde x}_R}}^2 $为$ {{\tilde x}_R} $的方差, 通过使用这些统计值，软误差方差可被估计为$ \beta = \sqrt {\frac{1}{{{\eta ^2} + \sigma _{\tilde n}^2}}} $.通过调用信道的对称性，BPSK调制和LDPC解码过程，可得出 ($ {{\tilde x}_R} $)=0, 由此得出 (${\tilde n} $)=0.

假设使用式 (2) 的模型，在第3个时隙中每个信源i接收到的信号可被写为$ {\mathit{\boldsymbol{y}}_{Ri}} = {\sqrt P _R}{h_{Ri}}{\beta _\eta }{x_R} + {{\mathit{\boldsymbol{\hat n}}}_{Ri}} $, 式中${{\mathit{\boldsymbol{\hat n}}}_{Ri}} = {\mathit{\boldsymbol{n}}_{Ri}} + \sqrt {{P_R}} {h_{Ri}}\beta \mathit{\boldsymbol{\tilde n}} $，$ {{\mathit{\boldsymbol{\hat n}}}_{Ri}}$是在目的节点处的总等效噪声.

对于第3个时隙传输的LLR可通过以下公式近似逼近：

$ {\lambda _{Ri}}\left( {x_R^j\left| {{y_{Ri}}} \right.} \right) = \log \left[ {\frac{{P\left( {x_R^j = + 1\left| {{y_{Ri}}} \right.} \right)}}{{P\left( {x_R^j = - 1\left| {{y_{Ri}}} \right.} \right)}}} \right] = \frac{{2\sqrt {{P}}_R {h_{Ri}}\beta \eta }}{{\hat \sigma _{Ri}^2}}y_{Ri}^j. $

对于软BPSK，提出模型下相对应的LLRλ(x_R^j|y_Ri) 为

$ \lambda \left( {x_R^j\left| {{y_{Ri}}} \right.} \right) = \frac{{2\sqrt {{P_R}} {h_{R\bar i}}\beta \left( {1 - {\mu _{\bar n}}} \right)}}{{\hat \sigma _{R\bar i}^2}}y_{R\bar i}^j. $

在信源i处于信源i相对应的先验LLR可被简单计算为$ {\lambda _{\bar ii}}(x_{\bar i}^j|{y_{\bar ii}}) = \frac{{2\sqrt {{P_{\bar i}}} {h_{\bar ii}}}}{{\bar \sigma _{\bar ii}^2}}y_{\bar ii}^j $.在信源i的网络解码软符号可通过以下公式计算:

$ {{\bar \lambda }_{Ri}}\left( {x_{\bar i}^j\left| {{\mathit{\boldsymbol{y}}_{Ri}}} \right.} \right) = {\lambda _{Ri}}\left( {x_R^j\left| {{\mathit{\boldsymbol{y}}_{Ri}}} \right.} \right) \cdot x_i^j. $

在目的节点，从中继和信源接收到的LLR将被加入，因为这是针对相同的底层信源第i个传输，其中i∈{A, B}.

2.1 等效单跳链路模型

为了分析提出方案的性能，给出了虚拟单跳链路的一个闭合形式的表达式，以代表在双向中继信道中两跳链路的等效信噪比及其他统计项.在链路i到R和链路R到i的瞬时信噪比分别定义为Γ_iR和Γ_Ri，其中Γ_iR=|h_iR|²P_S/σ_iR²，Γ_Ri=|h_iR|P_R/σ_iR²，i∈{A, B}，i∈{B, A}.

对于BPSK调制，只有在i-R的传输为正确接收，且R-i的传输为错误接收，或i-R的传输为错误接收且R-i的传输为正确接收的情况下，i处的信号在等效模型链接中才为错误接收.那么在中继处可得出如下误差概率：

$ \begin{array}{l} P_R^e\left( {{\mathit{\Gamma }_{AR}},{\mathit{\Gamma }_{BR}}} \right) = \left( {1 - P_{AR}^e\left( {{\mathit{\Gamma }_{AR}}} \right)} \right)P_{BR}^e\left( {{\mathit{\Gamma }_{BR}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {1 - P_{BR}^e\left( {{\mathit{\Gamma }_{BR}}} \right)} \right)P_{AR}^e\left( {{\mathit{\Gamma }_{AR}}} \right). \end{array} $

中继处的输出信噪比Γ_{eq, R}在虚拟等效单跳链路中可被计算为

$ {\mathit{\Gamma }_{eq,R}} = \frac{1}{\mathit{\Delta} }{\left( {{Q^{ - 1}}\left( {P_R^e\left( {{\mathit{\Gamma }_{AR}},{\mathit{\Gamma }_{BR}}} \right)} \right)} \right)^2}. $

式中: Q函数在形式上定义为$ Q(x) = \frac{1}{{\sqrt {2\pi } }}\int_x^\infty {\exp (\frac{{{u^2}}}{2}){\rm{d}}u} $，Q^-1(x) 是Q(x) 的反函数; Δ是取决于调配方案的常量, 对BPSK方案，Δ=2.这是通过单跳信噪比链接对双向中继信道的信噪比的一个近似.

现在能够对中继节点的输出信噪比Γ_{eq, R}进行约束，如下：

$ {\mathit{\Gamma }_{\min ,R}} - \frac{{3.24}}{\mathit{\Delta} } < {\mathit{\Gamma }_{eq,R}} < {\mathit{\Gamma }_{\min ,R}}, $

式中, Γ_{min, R}=min{Γ_AR, Γ_BR}.误差出现在目的节点，即由R发送的信息引起了i的错误且传输R-i是正确的，或中继R接收到的信息是正确的且传输R-i是错误的.

2.2 方差校正因子

一般而言，β的值和等效噪声方差$ \hat \sigma _{Ri}^2 $取决于软噪声方差$ \sigma _{\tilde n}^2 $和软标量η, 因为离线传输正确的符号x_R^j在中继处或目的节点处都是未知的.为解决这一问题，提出使用存储了$ \sigma _{\tilde n}^2 $的均值查找表.这些估计值通过使用分段线性插值法进行计算.用Γ_in表示在中继节点处接收到的信噪比，在中继处得到如下关系：

$ {\mathit{\Gamma }_{{\rm{in}}}} = \min \left\{ {{\mathit{\Gamma }_{AR}},{\mathit{\Gamma }_{BR}}} \right\}. $

式中，假设功率归一化P_A=P_B=P_R=1.用Γ_out表示中继节点的输出信噪比. SNR_iR和SNR_R分别为Γ_in和Γ_out的值，其中SNR_iR表示节点i和中继的信噪比，且SNR_R为中继节点处的输出信噪比.对于本文提出的模型，中继节点的输出信噪比为

$ {\mathit{\Gamma }_{{\rm{out}}}} = {\left| \eta \right|^2}/{P_{\mathit{\boldsymbol{\tilde n}}}}, $

式中，$ {P_{\tilde n}} = \frac{1}{{{N_1}}}\sum\nolimits_{j = 1}^{{N_1}} {|{{\tilde n}^j}{|^2}} $.该中继可以通过训练阶段中的Γ_in对Γ_out进行估计，并为瑞利衰减和加性高斯白噪声信道准备一个成对的表 (Γ_in, Γ_out).接着可以通过使用分段线性函数逼近Γ_out，即

$ {\mathit{\Gamma }_{{\rm{out}}}} = {a_k}{\mathit{\Gamma }_{{\rm{in}}}} + {b_k}. $

其中，在训练阶段估计成对的{(a_k, b_k)}_k，并存储在查找表中.

在对软误差和等效噪声$ {{\mathit{\boldsymbol{\hat n}}}_{Ri}} $的分析中，近似高斯分布的方差$\hat \sigma _{Ri}^2 $是不准确的，因为$ {\mathit{\boldsymbol{\tilde n}}} $的精确分布是未知的.这表明$ \hat \sigma _{Ri}^2 $与$ {{\mathit{\boldsymbol{\hat n}}}_{Ri}} = \sigma _{Ri}^2 + {P_R}h_{Ri}^2{\beta ^2}\sigma _{\tilde n}^2 $的近似高斯分布的方差并不完全一样, 主要是由于软误差变量${\mathit{\boldsymbol{\tilde n}}} $并没有服从高斯分布, 这与文献[8]提出的标准化模型相似.因此，为校正出现在目的节点的等效方差中的不精确性，引入了一个校正因子α，消除在目的节点处等效方差的不准确.基于这个论点，对等效噪声方差进行了如下修改：

$ \hat \sigma _{Ri}^2 = \sigma _{Ri}^2 + \alpha {P_R}h_{Ri}^2{\beta ^2}\sigma _{\tilde n}^2. $

式中，α是一个标量，用于校正在目的节点处的$ \hat \sigma _{Ri}^2 $，即方差校正因子，并通过仿真实验计算其数值. α的解析形式并不能轻松找到，因为软符号的概率分布是未知的.事实上，通过使用α，可以得到一个对$ \hat \sigma _{Ri}^2 $的校正标准，在目的节点处接收信号的方差.当α≤2时解码器对该方差具有敏感性，当α=2时可以得到较优性能.

3 仿真结果及分析 3.1 参数及参数设置

假设所有的信道都是准静态衰减，即信道系数h_AD、h_BD、h_RD、h_AR和h_BR对于每个传输阶段均为常数，从一个阶段到下一个阶段时独立地发生改变.实验中，中继固定在iR的信噪比等于1 dB，这是一个相对较差的信道环境.中继设置有两个假设:一个是对称中继设置，两个信源A和B与目的节点的距离相同，而且这两个信源中继节点和目的节点在同一水平线上对齐, 信源和目的节点之间的距离设置为d_AD=d_BD=1，衰减指数γ=2;另一个是非对称场景，其中一个信源距离中继节点比其他信源近，d_AR=0.7, d_BR=0.3，衰减指数γ=2.

在选择的SC-LDPC码中，N=2 425，K=1 455，码率P=0.6.在编码构建中，选择p=97，L=25，γ=3，k=5.对于包含瑞利衰落和中继信道的点对点加性高斯白噪声，最优分解 (在所有测试项中) 为δ=(5, 4, 2).该仿真实验假定BPSK和功率归一化，即P_A=P_B=P_R=1.在模拟的场景中，所有链路均经历瑞利衰落和加性高斯白噪声，并假定AR的信噪比等于BR的信噪比.

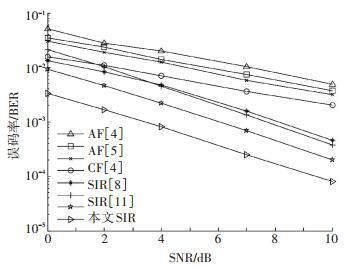
3.2 几种中继方案的比较分析

图 3给出了基于阵列空间耦合LDPC码的BER性能，从图 3可以看出，δ=(5, 4, 2) 表现出最优BER性能.因此，在接下来的仿真设置中，使用基于δ=(5, 4, 2)的空间耦合LDPC码.另外，还对参数K₁=111，N₁=185，码率=0.6的基于阵列LDPC分组码进行仿真，结果如图 3所示.该LDPC码作为构件用于基于阵列的SC-LDPC码中.需要指出的是，使用消息传递算法对分组LDPC码进行解码的延迟，与使用滑动窗口消息传递解码并适当选择解码窗口的大小，对LDPC分组码构建QC-LDPC码进行解码的延迟大致相当.

图 4给出了空间耦合LDPC编码的SIR方案与其他中继方案的比较，中继固定在iR的信噪比等于1 dB (相对较差的信道环境).使用空间耦合LDPC码对文献[8]的SIR方案进行仿真实验，SIR方案没有在中继处假定任何重编码.如图 4所示，以往提出的空间耦合LDPC码的SIR方案在瑞利衰落信道的误码率方面进行比较，前者明显优于后者.值得一提的是，本文在此没有假设任何软重新编码方案.另外，还对一个硬DF方案使用SC-LDPC码进行了仿真实验，作为一个基准方案.

当信源到中继信道条件较差时，目的节点将会出现解码误差.如果硬判定被中继节点转发到目的节点，则会产生巨大的误码扩散, 这就是本文在硬DF中取得了相对较差性能的原因.提出的方案在中继处不会做出轻易的判定，将软符号发送到目的节点.从完整性考虑，本文也对中继进行仿真.如预期的那样，由于在中继处的噪声放大，系统性能有所降低.

压缩-转发 (CF) 策略中，通过信源-中继链路发送的接收信号在一个中继节点中被量化和压缩，然后转发到目的节点.事实上，由于广播的性质，中继节点和目的节点接收到的信号具有相关性，本文也对CF进行了仿真实验.从图 4可以看到，提出的查找表方法与文献[11]中使用SC-LDPC码的SIR方案相比，稍微提高了BER性能.在文献[8]和文献[11]中，中继节点必须将所有LLR建模所需的参数转发到目的节点.此外，本文方案能够降低信令开销，因为中继节点只传输Γ_in.通过使用分段线性插值，目的节点可以创建任何组合的 (γ_in, γ_out, η).

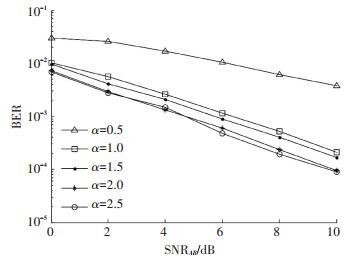
3.3 方差校正因子讨论

在图 5的仿真实验中，假设iR信噪比等于1，且iD信噪比等于Ri信噪比. 图 5的结果说明了提出的SIR方案在不同α值时的BER性能.在本文方案中，BER性能在α的值提高到α=2时得到了改善.在α>2的区域中，BER性能几乎保持不变，且没有对系统性能做出贡献.这一结果表明选择α=2接近最优解.当假定$ {{\mathit{\boldsymbol{\hat n}}}_{Ri}} $为一个近似高斯分布时，实际上低估了$ {{\mathit{\boldsymbol{\hat n}}}_{Ri}} $的实际方差.

接下来考虑非对称场景，其中一个信源距离中继节点比其他信源近.此处d_AR=0.7, d_BR=0.3. 图 5给出了不同α值的性能比较结果，即α = (0.5, 1, 1.5, 2, 2.5).从图 5可以观察到，提出的方案在α≈2时得到了最优性能.由图 5和图 6可知，当α=2时性能要优于α=1大概0.8 dB.随着Ri信噪比的提高，BER的性能也得到改善.对于$ {\tilde n} $未知的情况下找到α的一个分析解贯穿全文.因此，基于图 5中的仿真实验，总结认为α=2接近了最优解.

4 结论

提出的软信息中继优化方案没有选择对硬判决进行转发，而是转发修改的软网络编码符号.通过使用空间耦合的基于阵列LDPC码实现了误差校正, 还对软误差模型进行了修改，使得残留噪声的比例因子和软误差方差可以得到更简便的计算.这降低了信令开销，实现了更好的性能, 而校正因子参数是对目的节点处的软误差方差进行建模.相比于其他方案，提出的方案在误差率方面显著提高.