随着互联网技术的飞速发展,信息传递变得越来越方便、快捷.在享受科技进步带来便利的同时,信息安全隐患问题也应当引起注意,如被传递信息的非法窃取、恶意篡改甚至破坏.
隐写是一种信息隐藏技术,旨在利用数字形式的媒介 (视频、音频、图像等) 实现秘密信息的安全传送.通常情况下,优秀的图像隐写算法应具有两个特性:首先允许载体图像中被嵌入足够量的秘密信息,其次保证载密图像的抗隐写分析能力在可接受范围内.然而,在实际的隐写算法设计过程中,这两种需求是相互矛盾的,设计者在算法设计时,通常会在秘密信息嵌入率固定的条件下,设法提高隐写算法的抗检测性能.在现代隐写技术的发展过程中,最小化所有用于信息加密像素的损失和[1]被证明是一种可行的隐写设计方法.在这种思路框架下,设计者们提出了一系列行之有效的隐写算法[2-8],这些算法的设计过程可以归结为两步:首先以最小加性失真模型为基础确定出损失函数,用于计算嵌入秘密信息造成的像素损失和;然后根据损失函数进行隐写编码嵌入信息. Filler等[9]在最小化加性失真模型的框架下提出一种校验格编码方法STC (syndrome trellis coding),并给出证明,按照设计者自定义的损失函数,使用STC编码时的编码效率可以接近理论上限,STC编码技术的提出将隐写算法设计简化到了损失函数设计上. Holub等[5]利用DB-8小波构造的方向性滤波器组设计损失函数,提出应用于空间域的隐写算法WOW (Wavelet Obtained Weights),之后又将WOW算法从空间域推广到了任意域,提出UNIWARD (UNIversal WAvelet Relative Distortion) 算法[7].空域UNIWARD算法与WOW算法在损失函数上仅相差一个常数,两种算法在空域富模型SRM (spatial rich models) [10]下的抗检测性能基本一致. LiBin等利用KB预测算子[11]与两个均值滤波器设计损失函数,提出HILL (high-pass, low-pass, low-pass) 算法[8].以上提到的三种算法都是当今主流的隐写算法,其中,HILL算法拥有最强的抗富模型检测能力.
为改善利用方向性滤波器获取载体图像纹理区域的性能,提升隐写算法的安全性能,在WOW算法模型的基础上,本文提出一种利用Gabor小波设计的空域自适应隐写算法.首先利用Gabor小波构造的方向性滤波器组分别从8个方向对载体图像进行残差权重预测,获取载体图像纹理丰富区域,并以Hölder范数形式定义损失函数;然后利用均值滤波器对所得损失函数进行滤波处理得到新的损失函数;最后通过STC编码按照最终得到的损失函数在载体图像中嵌入秘密信息.抵抗富模型检测实验结果表明,同等水平的信息嵌入率下,所提算法的安全性能优于同类隐写算法.
1 相关基础 1.1 WOW算法的损失函数WOW算法[5]中的损失函数由Daubechies 8-tap (DB-8) 小波构成的方向性滤波器组设计得到.首先利用DB-8小波预测载体图像的残差权重,找到合适的信息嵌入位置ξij(k):
| $\xi _{ij}^{\left( k \right)} = \left| {X \otimes {K^{\left( k \right)}}} \right| \otimes \left| {R\left( {{K^{\left( k \right)}}} \right)} \right|.$ |
式中:X为载体图像,K(k)为DB-8构成的方向性滤波器组 (k=1, 2, 3),R表示将K(k)翻转180°.然后将ξij(k)以Hölder范数形式构造成损失函数ρ:
| ${\rho _{ij}} = {\left( {\sum\nolimits_{k = 1}^3 {{{\left| {\xi _{ij}^{\left( k \right)}} \right|}^p}} } \right)^{ - \frac{1}{p}}},$ |
式中p在WOW算法中的取值为-1.
通过DB-8小波对载体图像LH,HL,HH这3个方向进行残差权重预测,WOW算法可以利用STC编码将秘密信息嵌入到从LH,HL和HH方向中任一方向都难以建模分析的纹理复杂区域.利用WOW算法加密时,对一张载体图像的3方向分解如图 1所示,其中图 1(a)为载体图像,图 1(b)、(c)、(d)为DB-8小波对载体的3方向分解.

|
图 1 DB-8小波对载体图像的3方向分解 Figure 1 3 direction decompositions of cover image using DB-8 wavelet |
STC[9]是一种特殊的应用于隐写技术中的矩阵编码,在损失函数确定的情况下,它可以将最小化嵌入失真问题转化为寻找最短路径问题,后者可以通过维特比译码快速得到.
假设载体图像为x,载密图像为y,秘密信息为m,则使用STC编码嵌入信息时,三者间应满足HyT=m的关系, 式中H为稀疏奇偶校验矩阵,由若干个大小为h×w的
假设
| $\mathit{\boldsymbol{H = }}\left\{ {\begin{array}{*{20}{l}} 1 & 0 & {} & {} & {} & {} & {} & {} & {} & {}\\ 0 & 1 & 1 & 0 & {} & {} & {} & {} & {} & {}\\ {} & {} & 0 & 1 & 1 & 0 & {} & {} & {} & {}\\ {} & {} & {} & {} & 0 & 1 & \cdots & {} & {} & {}\\ {} & {} & {} & {} & {} & {} & {} & 1 & 0 & {}\\ {} & {} & {} & {} & {} & {} & {} & 0 & 1 & 1 \end{array}} \right.\left. {\begin{array}{*{20}{l}} {}\\ {}\\ {}\\ {}\\ {}\\ {\quad 0} \end{array}} \right).$ |
根据公式HyT=m,秘密信息接收者可以方便地计算出被发送的信息.
2 基于Gabor小波的空域自适应隐写算法 2.1 Gabor小波在图像处理中,Gabor小波滤波器是一个用于边缘提取的线性滤波器,其频率和方向表达同人类视觉系统类似. Gabor小波十分适合纹理表达和分离[12],且现在已有大量成功应用于模式识别的案例[13-15].
在空间域中,二维Gabor小波函数是由正弦平面波调制的高斯核函数,即
| $\begin{array}{l} G = \left( {x,y} \right) = \frac{{{f^2}}}{{\pi \gamma \eta }}\exp \left( { - \left( {{\alpha ^2}{x_1}^2 + {\beta ^2}{y_1}^2} \right)} \right)\exp \left( {{\rm{j}}2{\rm{ \mathsf{ π} }}f{x_1}} \right),\\ \quad \quad \quad \quad \quad \quad \quad {x_1} = x\cos \theta + y\sin \theta ,\\ \quad \quad \quad \quad \quad \quad \quad {y_1} = - x\sin \theta + y\cos \theta ,\\ \end{array}$ |
式中:f为正弦平面波的中心频率;θ为高斯函数逆时针旋转的角度;γ和η控制高斯函数的频率和锐度,且α=f/γ,β=f/η.
本文尝试将Gabor小波应用于隐写算法设计,通过调整高斯函数的旋转角度θ,利用Gabor小波构造一个8方向的滤波器组.所提算法中θ的取值分别为0、π/8、2π/8、3π/8、4π/8、5π/8、6π/8、7π/8,每个方向小波中其他关键参数的取值分别为f=0.325,γ=1,η=1,滤波器组方向数选取和参数优化过程将在实验部分给出.利用方向性滤波器组将载体图像分解,损失函数将会被定义为不同方向上因嵌入信息造成分解系数发生相对变化之和.滤波器组的多方向性使得加密后的载体图像在其8方向中的任一方向都难以被建模分析,减小秘密信息被隐写分析算法检测到的可能性.所提算法隐写时对一张载体图像的8方向分解见图 2,其中图 2(a)为载体图像,图 2(b)~(i)为Gabor小波对载体图像的8方向分解.

|
图 2 Gabor小波对图像的8方向分解 Figure 2 8 direction decompositions of cover image using Gabor wavelet |
WOW算法利用DB-8小波构造的方向性滤波组从LH、HL和HH这3个方向计算载体图像残差值权重,将秘密信息嵌入到LH、HL、HH任一方向都难以预测建模的区域.本文算法在WOW算法基础上做出改进,利用Gabor小波方向性滤波器组取代DB-8小波方向性滤波器组,将秘密信息嵌入到0、π/8、2π/8、3π/8、4π/8、5π/8、6π/8、7π/8任一方向都难以预测建模的区域.所提算法 (记为Proposed) 的隐写过程如下:
1) 利用Gabor小波方向性滤波器组预测载体图像的残差权重,计算其中合适的信息嵌入位置ξij(k):
| $\xi _{ij}^{\left( k \right)} = \left| {X \otimes {G^{\left( k \right)}}} \right| \otimes \left| {{\rm{R}}\left( {{G^{\left( k \right)}}} \right)} \right|.$ |
式中:X为载体图像,G(k)为Gabor构成的方向性滤波器组 (k=1, 2, 3, …, 8),R表示将G(k)翻转180°.
2) 将ξij(k)以Hölder范数形式构建损失函数ρ:
| ${\rho _{ij}} = \left( {\sum\nolimits_{k = 1}^8 {{{\left| {\xi _{ij}^{\left( k \right)}} \right|}^{ - 1}}} } \right).$ |
3) 假设秘密信息为m∈{m1, m2, m3, …, mk},k为信息长度,载体图像X的LSB层为xx={xxn},载密图像Y的LSB层为xy={xyn},若xxn=xyn,保持X中的像素点不变;若xxn≠6xyn,利用损失函数和STC编码在X中嵌入信息.
2.3 改进算法使用自适应隐写算法的最终目的是将秘密信息嵌入到载体图像中纹理丰富的复杂区域,然而当载体图像比较平滑或信息嵌入量较大时,嵌入的秘密信息有可能散落到图像平滑区域或一些孤立点像素中,通过建模分析,隐写分析者可以轻易地探测到此类信息,从而降低了算法的安全性.文献[16]指出,利用聚焦改变位置策略减少此类秘密信息的存在,可以有效提高算法的抗检测性能.
基于以上思想,对所提算法做出进一步改进:在信息嵌入之前,利用均值滤波器对损失函数进行滤波,滤除相对孤立点像素的残差权重,尽量使残差权重集中到纹理丰富区域,减小秘密信息被嵌入到载体图像平滑区域的可能性.更新后的损失函数ρA为
| ${\rho _{\rm{A}}} = {\rho _{ij}} \otimes A = \left( {\sum\nolimits_{k = 1}^8 {{{\left| {\xi _{ij}^{\left( k \right)}} \right|}^{ - 1}}} } \right) \otimes A.$ |
式中A为均值滤波器,在本文算法中的阶数为13,具体参数值的讨论将在实验部分给出.损失函数更新后,按照2.2节中的步骤3) 继续进行秘密信息嵌入.应用聚焦位置改变策略的所提算法记为Proposed-A.
3 实验分析实验计算机及软件配置如下:Intel Core i3 2.40 GHz CPU、4.00 GB RAM,软件平台为MATLAB R2014a.用于安全性测试的图像库有两个,分别为BOSSBase 1.01[17]和BOWS2[18].借助34671维SRM特征和12753维SRMQ1特征衡量算法抗隐写分析性能,提取好的载体图像和载密图像特征分别送至集成分类器[19]进行分类,分类过程中一半图像特征用于训练,另一半用于测试.最终的分析结果以检测错误率的形式给出,检测错误率越高,算法安全性能越好,反之亦然.安全性对比分析中应用到的自适应隐写算法有HUGO-BD[3]、WOW[5]、HILL[8]、Proposed、Proposed-A,除本文算法外,其他算法中的参数均为原文献默认值.
3.1 秘密信息的自适应嵌入网络中传输的大多数数字图像都会存在纹理丰富的复杂区域和相对平滑的简单区域,相关研究表明[20],将秘密信息嵌入到纹理丰富区域可有效提升加密图像抵抗隐写分析的能力.所提算法考虑了载体图像的自身特性,利用Gabor小波从8个方向对其进行分解,获取纹理丰富区域,再利用STC编码在纹理丰富区域中嵌入秘密信息,最终实现自适应隐写.通过一组实验说明秘密信息的自适应嵌入情况. 图 3(a)为载体图像,利用Proposed算法和Proposed-A算法对其进行隐写,信息嵌入率为0.4 bit/pixel,加密后载体图像中的秘密信息分布分别如图 3(b)和图 3(c)所示,其中,白色像素点表示秘密信息.载体图像经Gabor小波处理后得到的纹理丰富区域可见图 2.由图 2和图 3可知,通过考虑图 3(a)的自身特性,所提算法借助Gabor小波和STC编码技术将秘密信息嵌入到了其纹理丰富区域,最终实现了自适应隐写.

|
图 3 所提算法隐写后的秘密信息分布 Figure 3 Distribution of secret message after steganography by Proposed and Proposed-A algorithm |
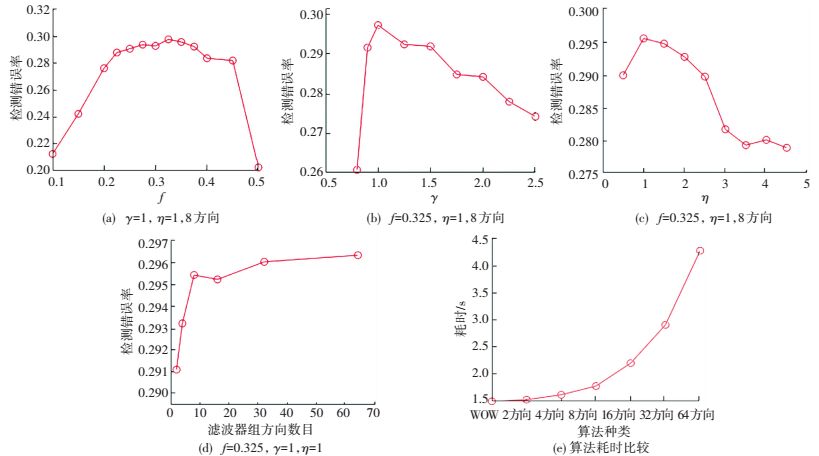
为构造最优的Gabor小波方向性滤波器组,借助WOW算法模型分别对Gabor小波中的参数f、γ、η进行优化,并确定出滤波器组的方向数,其中,滤波器组的方向数由参数θ决定.优化共有两个过程,先设置参数θ为定值,求出最佳的f、γ、η参数值,再对参数θ进行优化.
首先设定滤波器组方向数为8,即参数θ分别取值0、π/8、2π/8、…、7π/8,固定参数γ、η取值,控制参数f在一定范围内变化,检测f发生变化时所提算法Proposed的抗检测能力.选取安全性最好的那组参数f作为最佳参数,隐写算法的构造方式可参见2.2节,最佳参数确定后即设定其为固定值,另外两个参数γ、η的优化过程与参数f相同.求出参数f、γ、η的最佳值后将其固定,令滤波器组方向数分别为2(θ=0、π/2)、4(θ= 0、π/4、2π/4、3π/4)、8(θ= 0、π/8、2π/8、…、7π/8)、16(θ= 0、π/16、2π/16、…、15π/16)、32(θ=0、π/32、2π/32、…、31π/32)、64(θ=0、π/64、2π/64、…、63π/64),检测滤波器组方向数发生变化时所提算法的抗检测能力.进行抗检测性能分析实验时,随机从Bossbase 1.01图像库中选取5 000张图像用于隐写加密,信息嵌入率为0.4 bit/pixel,提取载体图像和载密图像SRMQ1特征送至集成分类器进行分类,根据分类结果确定算法抗检测性能.
实验数据见图 4.由图 4(a)、图 4(b)、图 4(c)确定出参数f、γ、η最佳值分别为0.325、1、1.由图 4(d)、图 4(e)可知,随着滤波器组方向数增多,所提算法的抗检测性能大致呈上升趋势,但当滤波器组方向数明显增大时,所提算法的安全性能的提升并不明显,而隐写单张载体图片的耗时明显增加.
|
图 4 方向性滤波器的参数优化 Figure 4 Parameters optimization of directional filter |
综合考虑算法的安全性能与时间复杂度,最终确定滤波器组方向数为8.另外,由图 4(e)可知,在时间复杂度上WOW比所提算法有0.3 s左右的优势,两者之间的差距并不大,且隐写技术中最重要的两个指标是算法安全性能和信息嵌入率,因此可以忽略两者在时间复杂度上的差距.
3.3 A参数讨论Proposed-A通过聚焦改变位置策略对所提算法做进一步改进,为确定均值滤波器A的参数值,做以下实验:选取Bossbase 1.01图像库中的10 000张图像用于测试,选用不同A参数的Proposed-A进行隐写加密,信息嵌入率为0.4 bit/pixel,加密完成后利用SRMQ1提取载体图像和载密图像特征,最后将提取好的特征送至集成分类器进行分类,实验数据如表 1所示.
| 表 1 均值滤波器对Proposed-A安全性能的影响 Table 1 Effect of average filter on Proposed-A |
在Bossbase 1.01图像库上的实验表明,与Proposed相比,应用了聚焦改变策略的Proposed-A的抗检测性能有0.6%~2.6%的提升.根据实验结果,最终确定Proposed-A中的均值滤波器阶数为13×13.
3.4 算法安全性对比为对比分析算法的抗检测性能,分别利用12753维SRMQ1特征和34671维SRM特征对HUGO-BD、WOW、Proposed、HILL和Proposed-A进行安全性能检测分析,隐写载体分别选用Bossbase 1.01图像库中的10 000张和BOWS2图像库中的5 000张空域灰度图像,信息嵌入率分别为0.05、0.1、0.2、0.3、0.4、0.5 bit/pixel.最终的分类错误率结果分别如表 2、图 5和图 6所示,详细的实验数据可参见表 2.
| 表 2 抗SRMQ1和SRM特征检测性能分析 Table 2 Security analysis of detected by SRMQ1 and SRM |
|
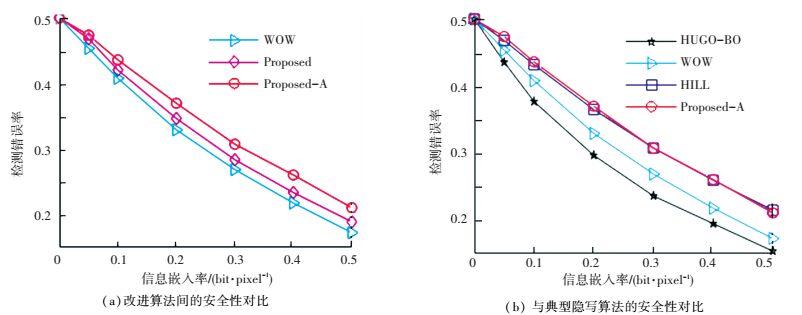
图 5 BOSSBase1.01图像库上的SRMQ1隐写分析 Figure 5 SRMQ1 steganalysis on BOSSBase 1.01 |
|
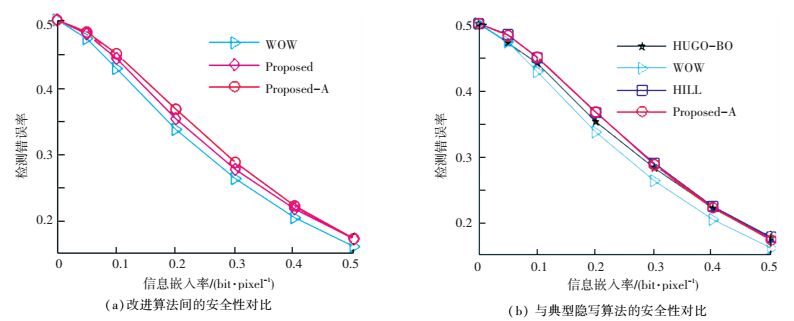
图 6 BOWS2图像库上的SRMQ1隐写分析 Figure 6 SRMQ1 steganalysis on BOWS2 |
由图 5(a)和图 6(a)可知,由Gabor小波方向性滤波器组设计的Proposed算法的抵抗富模型检测能力强于WOW,与Proposed算法相比,对信息嵌入位置做出调整后,引入聚焦改变位置策略的Proposed-A算法在抗富模型检测能力上又有了一定幅度的增强;从图 5(b)和图 6(b)可知,与其他自适应隐写算法相比,本文算法同样存在一定优势,在两个不同数据库测试时,同等水平的信息嵌入率条件下,Proposed-A算法的抗检测性能略优于HILL算法或与之相当,均优于WOW和HUGO-BD.分析其原因,Gabor小波在生物图像纹理表达和分离上的优势特性同样有利于自适应隐写算法中信息嵌入位置的确定,且与利用3方向滤波器组设计的WOW算法相比,所提算法可以将秘密信息嵌入到从8个方向上都难于被建模分析的纹理复杂区域.另外,应用聚焦改变位置策略后,所提算法可以减少秘密信息被嵌入到平滑区域的可能性,这同样有利于算法安全性能的提升.
4 结语在WOW算法的基础上,提出一种利用Gabor小波设计的空域自适应隐写算法,并通过聚焦改变位置策略对所提算法做出了进一步完善.本文将Gabor小波应用到隐写术中,通过Gabor小波获取载体图像的纹理丰富区域,构造好损失函数后再利用校验格编码完成秘密信息嵌入,最终实现自适应隐写.实验表明,所提算法的安全性能明显优于WOW算法,从而验证了本文方案的可行性.另外,与HUGO-BD算法和HILL算法相比,所提算法同样存在一定优势.
| [1] | FRIDRICH J, FILLER T. Practical methods for minimizing embedding impact in steganography[J]. Proceedings of SPIE-The International Society for Optical Engineering, 2007, 6505: 650502-650502. DOI: 10.1117/12.697471 |
| [2] | PENVY T, FILLER T, BAS P. Using high-dimensional image models to perform highly undetectable steganography[C]// International Conference on Information Hiding. Calgary:Springer-Verlag, 2010: 161-177. DOI: 10.1007/978-3-642-16435-4_13. |
| [3] | FILLER T, FRIDRICH J. Gibbs construction in steganography[J]. IEEE Transactions on Information Forensics and Security, 2010, 5(4): 705-720. DOI: 10.1109/TIFS.2010.2077629 |
| [4] | GUO Linjie, NI Jiangqun, SHI Yunqing. An efficient JPEG steganographic scheme using uniform embedding[J]. IEEE International Workshop on Information Forensics and Security, 2012, 98(5): 169-174. DOI: 10.1109/WIFS.2012.6412644 |
| [5] | HOLUB V, FRIDRICH J. Designing steganographic distortion using directional filters[J]. IEEE International Workshop on Information Forensics and Security, 2012, 2(4): 234-239. DOI: 10.1109/WIFS.2012.6412655 |
| [6] | GUO Linjie, NI Jiangqun, SHI Yunqing. Uniform embedding for efficient JPEG steganography[J]. IEEE Transactions on Information Forensics and Security, 2014, 9(5): 814-825. DOI: 10.1109/TIFS.2014.2312817 |
| [7] | HOLUB V, FRIDRICH J, DENEMARK T. Universal distortion function for steganography in an arbitrary domain[J]. Eurasip Journal on Information Security, 2014, 2014(1): 1-13. DOI: 10.1186/1687-417X-2014-1 |
| [8] | LI Bin, WANG Ming, HUANG Jiwu, et al. A new cost function for spatial image steganography[C]// IEEE International Conference on Image Processing. Paris: IEEE, 2014: 4206-4210. |
| [9] | FILLER T, JUDAS J, FRIDRICH J. Minimizing additive distortion in steganography using syndrome-trellis codes[J]. IEEE Transactions on Information Forensics and Security, 2011, 6(3): 920-935. DOI: 10.1109/TIFS.2011.2134094 |
| [10] | FRIDRICH J, KODOVSKY J. Rich models for steganalysis of digital images[J]. IEEE Transactions on Information Forensics and Security, 2012, 7(3): 868-882. DOI: 10.1109/TIFS.2012.2190402 |
| [11] | HOLUB V, FRIDRICH J. Optimizing pixel predictors for steganalysis[J]. Proceedings of SPIE-The International Society for Optical Engineering, 2012, 8303: 830309-830309. DOI: 10.1117/12.905753 |
| [12] | MANJUNATHB S, MA W Y. Texture features for browsing and retrieval of image data[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1996, 18(8): 837-842. DOI: 10.1109/34.531803 |
| [13] | ZHANG Baochang, SHAN Shiguang, CHEN Xilin, et al. Histogram of gabor phase patterns (HGPP): a novel object representation approach for face recognition[J]. IEEE Transactions on Image Processing, 2007, 16(1): 57-68. DOI: 10.1109/TIP.2006.884956 |
| [14] | REN Chuanxian, DAI Daoqing, LI Xiaoxin, et al. Band-reweighed gabor kernel embedding for face image representation and recognition[J]. IEEE Transactions on Image Processing, 2014, 23(2): 725-740. DOI: 10.1109/TIP.2013.2292560 |
| [15] | DOSODIA P, POONIA A, GUPTA S K, et al. New Gabor-DCT feature extraction technique for facial expression recognition[C]// Fifth International Conference on Communication Systems and Network Technologies. Gwalior: IEEE, 2015. DOI: 10.1109/CSNT.2015.162. |
| [16] |
王明. 最小化嵌入失真图像隐写的代价函数设计[D]. 深圳: 深圳大学, 2015.
WANG Ming. Cost function design for image steganography under embedding distortion minization[D].Shenzhen:Shenzhen University, 2015. |
| [17] | BAS P, FILLER T, PENVY T. Break our steganographic system: the ins and outs of organizing BOSS[C]// International Conference on Information Hiding. Prague: Springer-Verlag, 2011: 59-70.DOI:10.1109/TIFS.2010.2077629. |
| [18] | BAS P, FURON T.BOWS-2. http://bows2.gipsa-lab.inpg.fr.2007. |
| [19] | KODOVSKY J, FRIDRICH J, HOLUB V. Ensemble classifiers for steganalysis of digital media[J]. IEEE Transactions on Information Forensics and Security, 2012, 7(2): 432-444. DOI: 10.1109/TIFS.2011.2175919 |
| [20] |
奚玲. 基于内容特征的自适应图像隐写技术研究[D]. 郑州: 解放军信息工程大学, 2011.
XI Ling. Research on content based adaptive image steganograghy[D]. Zhengzhou:PLA Information Engineering University, 2011. |
 2017, Vol. 49
2017, Vol. 49


