2. 武汉大学 动力与机械学院,武汉 430072
2. School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China
高分辨率海底地形在水下管节安放、沉船打捞、油气勘探和环境监测等海洋工程和科学研究中发挥着重要作用[1-5].目前海底地形主要借助单波束或多波束测深系统获得.单波束测深分辨率与测线和测点间隔相关,精细的海底地形需通过密集布线和繁重的外业测量才能获得;多波束具有全覆盖、面扫测地形的能力,但测深分辨率会随波束入射角和水深增大而降低.海底地貌可借助侧扫声呐系统SSS (side-scan sonar) 扫测成像获得,所得图像分辨率是多波束测深分辨率的20~100倍,可表征海底微地貌特征,但缺少高程信息[5].若能够利用SSS图像获得海底三维地形,则可为高分辨海底地形的获取提供一种新途径.
Shape From Shading (SFS) 借助计算机视觉理论,根据图像明暗变化获取物体表面相对高度,是实现三维形状恢复的一项关键技术[6-13]. SFS通过解决成像建模和模型求解两个关键问题实现形状恢复.文献[7]总结了不同类型SFS反演算法的性能;文献[8]对近点光源透视成像下的辐照度方程进行了推导;文献[9]研究了透视投影下远点和近点光源照射Lambert反射体表面的建模问题,并考虑了光能的衰减影响;文献[10]研究了非Lambert体的建模问题;文献[11]采用Ward反射模型开展了混合表面建模问题研究;文献[12-13]分别改进了文献[9]的方法,提高了模型求解效率.基于以上理论研究,文献[14]对模拟沙坡声呐图像进行反演,得到了沙坡形状;文献[15]将多分辨率技术和期望最大算法与SFS算法结合,提高了反演方法的可靠性;文献[16-17]应用SFS技术由SSS图像得到了海底目标形状.已有研究为SSS图像反演海底三维地形奠定了理论基础,但这些研究均为基于图像的目标形状反演,目标的绝对尺寸尚未给出;此外,声呐成像与光学成像不同,直接借助基于光照理论的SFS算法开展海底地形反演,在机理上尚存在不足.为此,本文基于SFS理论,结合SSS成像机理,提出一种SSS图像反演海底绝对地形的线性方法,以期实现高分辨率海底地形的获取.
1 地形反演方法 1.1 SFS反演理论基础若物体表面粗糙,SFS理论认为,光在物体表面遵循Lambert漫反射,反射强度与光入射方向 (ps, qs, -1)、表面梯度 (p, q) 等相关,据此给出了Lambert反射模型为[7-9, 14-15]
| $ \begin{array}{l} E\left( {x,y} \right) = R\left( {p,q} \right) = \frac{{1 + p{p_{\rm{s}}} + q{q_{\rm{s}}}}}{{\sqrt {1 + {p^2} + {q^2}} \sqrt {1 + p_{\rm{s}}^2 + p_{\rm{s}}^2} }} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\cos \varphi + p\cos \tau \sin \varphi + q\sin \tau \sin \varphi }}{{\sqrt {1 + {p^2} + {q^2}} }}. \end{array} $ | (1) |
式中:E (x, y)为归一化强度 (或图像强度),x和y为图像坐标,R为反射模型函数,τ和φ分别为声波入射方向的偏角和倾角.若Z为地形值,则表面x、y方向梯度p、q为
| $ \left\{ \begin{array}{l} p = \frac{{\partial Z}}{{\partial x}} = Z\left( {x,y} \right) - Z\left( {x - 1,y} \right),\\ q = \frac{{\partial Z}}{{\partial y}} = Z\left( {x,y} \right) - Z\left( {x,y - 1} \right). \end{array} \right. $ | (2) |
根据以上SFS反演思想,对于SSS图像,在已知归一化的回波强度 (或图像强度) 和声波入射方向后,即可根据式 (1)、(2) 解算海底地形.该解算过程主要包括如下步骤:
1) 传统SFS反演研究认为光照平行到达目标表面,而SSS图像的声源来自于换能器,因此需要根据其成像机理计算式 (1) 中的波束入射方向参数.
2) 已知声波入射方向,结合漫反射模型,推导SSS图像反演海底地形的线性模型.
3) 以外部测深数据作为约束条件,实现反演地形向绝对地形的转变.
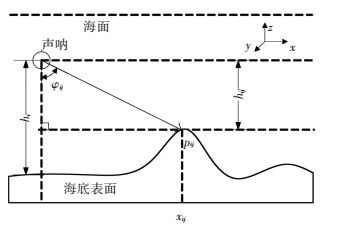
1.2 声波入射方向估算SSS测量时分别向两侧发射声波,打到海底返回并被换能器接收,工作原理如图 1所示.
|
图 1 侧扫声呐工作原理和声波入射方向示意 Figure 1 The schematic diagram of sonar operating mechanism and sound incident direction |
第i ping第j个像素的入射方向向量表示为
| $ {R_{ij}} = \left( {\frac{{\cos {\tau _{ij}}\sin {\varphi _{ij}}}}{{\cos {\varphi _{ij}}}},\frac{{\sin {\tau _{ij}}\sin {\varphi _{ij}}}}{{\cos {\varphi _{ij}}}}, - 1} \right). $ |
式中:τij是声波入射方向的偏角,φij是声波入射方向的倾角.当侧扫声呐的航迹线与y轴一致时,偏角为0.若已知拖鱼到海底高度和初始海底地形,根据声波入射方向示意图 (如图 1所示),可给出
| $ \begin{array}{*{20}{c}} {{\varphi _{ij}} = \arctan \left( {\frac{{{x_{ij}}}}{{{h_{ij}}}}} \right),}\\ {{h_{ij}} = {h_i} - \left( {{\rm{Zi}}{{\rm{n}}_{ij}} - \min \left\{ {{\rm{Zi}}{{\rm{n}}_{ij}}} \right\}} \right).} \end{array} $ |
式中:xij是 (i, j) 像素对应测点pij到船体坐标系y轴的距离,hi为拖鱼到海底高度,hij是pij至拖鱼面的垂直距离,Zinij为pij初始深度,min{Zinij}是每ping初始地形的最小值.
1.3 反演模型获得了声波入射方向后,对SSS图像强度归一化,即将图像的0~255灰度级转换到0~1.在此基础上,对SSS图像反演海底地形的模型进行推导,变换式 (1) 和 (2) 可得
| $ \begin{array}{l} 0 = f\left( {E\left( {x,y} \right),Z\left( {x,y} \right),Z\left( {x - 1,y} \right),Z\left( {x,y - 1} \right)} \right) = \\ \;\;\;\;\;\;E\left( {x,y} \right) - R\left( {Z\left( {x,y} \right) - Z\left( {x - 1,y} \right),Z\left( {x,y} \right) - } \right.\\ \;\;\;\;\;\;\left. {Z\left( {x,y - 1} \right)} \right). \end{array} $ | (3) |
对式 (3) 进行泰勒级数展开为
| $ \begin{array}{l} 0 = f\left( {E\left( {x,y} \right),{Z^{n - 1}}\left( {x,y} \right),{Z^{n - 1}}\left( {x - 1,y} \right),{Z^{n - 1}}\left( {x,y - } \right.} \right.\\ \;\;\;\;\;\left. {\left. 1 \right)} \right) + F\left( 1 \right) + F\left( 2 \right) + \cdots + F\left( n \right), \end{array} $ | (4) |
式中F(1),F(2),…,F (n)为模型的1, 2…, n阶项.
| $ \begin{array}{l} F\left( 1 \right) = {a_{x,y}}\left( {Z\left( {x,y} \right) - {Z^{n - 1}}\left( {x,y} \right)} \right) + {a_{x - 1,y}}\left( {Z\left( {x - } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\left. {1,y} \right) - {Z^{n - 1}}\left( {x - 1,y} \right)} \right) + {a_{x,y - 1}}\left( {Z\left( {x,y - } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\left. 1 \right) - {Z^{n - 1}}\left( {x,y - 1} \right)} \right),\\ F\left( 2 \right) = \frac{1}{2}{b_{x,y}}\left( {^Z\left( {x,y} \right) - {Z^{n - 1}}\left( {x,y} \right)} \right)2 + \frac{1}{2}{b_{x - 1,y}}\frac{1}{n}\left( {^Z\left( {x - } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\left. {1,y} \right) - {Z^{n - 1}}\left( {x - 1,y} \right)} \right)2 + \frac{1}{2}{b_{x,y - 1}}\left( {^Z\left( {x,y - } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\left. 1 \right) - {Z^{n - 1}}\left( {x,y - 1} \right)} \right)2 + c_{x - 1,y}^{x,y}\left( {Z\left( {x,y} \right) - } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {{Z^{n - 1}}\left( {x,y} \right)} \right)\left( {Z\left( {x - 1,y} \right) - {Z^{n - 1}}\left( {x - 1,y} \right)} \right) + \\ \;\;\;\;\;\;\;\;\;\;c_{x,y - 1}^{x,y}\left( {Z\left( {x,y} \right) - {Z^{n - 1}}\left( {x,y} \right)} \right)\left( {Z\left( {x,y - 1} \right) - } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {{Z^{n - 1}}\left( {x,y - 1} \right)} \right) + c_{x,y - 1}^{x - 1,y}\left( {Z\left( {x - 1,y} \right) - {Z^{n - 1}}\left( {x - } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\left. {1,y} \right)} \right)\left( {Z\left( {x,y - 1} \right) - {Z^{n - 1}}\left( {x,y - 1} \right)} \right),\\ {a_{xy}} = \frac{{\partial f}}{{\partial Z\left( {x,y} \right)}},\;\;{b_{xy}} = \frac{{{\partial ^2}f}}{{\partial Z{{\left( {x,y} \right)}^2}}},\\ c_{x - 1,y}^{x,y} = \frac{{{\partial ^2}f}}{{\partial Z\left( {x,y} \right)\partial Z\left( {x - 1,y} \right)}}. \end{array} $ |
对于图像上每个像素单元,均可给出式 (4) 所示方程.采用式 (5) 所示关系,利用牛顿迭代法求解地形Z:
| $ {Z^n}\left( {x,y} \right) = {Z^{n - 1}}\left( {x,y} \right) + \frac{{ - {K_n} - \sqrt {{{\left( {{K^n}} \right)}^2} - 2{L^n}f\left( {{Z^{n - 1}}\left( {x,y} \right)} \right)} }}{{{L^n}}}, $ | (5) |
其中
| $ \begin{array}{l} {K_n} = \frac{{df\left( {{Z^{n - 1}}\left( {x,y} \right)} \right)}}{{{\rm{d}}Z\left( {x,y} \right)}} = - \frac{{\left( {{p_{\rm{s}}} + {q_{\rm{s}}}} \right)}}{{\sqrt {{p^2} + {q^2} + 1} \sqrt {p_{\rm{s}}^2 + q_{\rm{s}}^2 + 1} }} + \\ \;\;\;\;\;\;\;\;\frac{{\left( {p + q} \right)\left( {p{p_{\rm{s}}} + q{q_{\rm{s}}} + 1} \right)}}{{\sqrt {{{\left( {{p^2} + {q^2} + 1} \right)}^3}} \sqrt {p_{\rm{s}}^2 + q_{\rm{s}}^2 + 1} }},\\ {L^n} = \frac{{{d^2}f\left( {{Z^{n - 1}}\left( {x,y} \right)} \right)}}{{{\rm{d}}Z{{\left( {x,y} \right)}^2}}} = \\ \;\;\;\;\;\;\;\frac{{2\left( {p + q} \right)\left( {{p_{\rm{s}}} + {q_{\rm{s}}}} \right) + 2\left( {1 + p{p_{\rm{s}}} + q{q_{\rm{s}}}} \right)}}{{\sqrt {1 + p_{\rm{s}}^2 + q_{\rm{s}}^2} \sqrt {{{\left( {1 + {p^2} + {q^2}} \right)}^3}} }} - \\ \;\;\;\;\;\;\;\frac{{3{{\left( {p + q} \right)}^2}\left( {1 + p{p_{\rm{s}}} + q{q_{\rm{s}}}} \right)}}{{\sqrt {1 + p_{\rm{s}}^2 + q_{\rm{s}}^2} \sqrt {{{\left( {1 + {p^2} + {q^2}} \right)}^5}} }}. \end{array} $ |
若设定迭代阈值ε,则迭代的终止条件为
| $ {Z^n}\left( {x,y} \right) - {Z^{n - 1}}\left( {x,y} \right) \le \varepsilon . $ | (6) |
由以上迭代过程可以看出,若给定初始地形Z0,经过若干次迭代后,则可得到最终的地形Z.以上不但给出了适合SSS图像反演海底地形的实用模型,同时解决了传统SFS反演所得相对地形形状向实际绝对地形转换的问题.
1.4 海底绝对地形反演基于以上研究,基于SSS图像的海底地形反演过程如下:
1) 根据各像素对应的船体坐标系坐标、拖鱼高度、基于概略地形得到的海底点概略高度等信息,计算各像素对应的波束概略入射方向;
2) 根据外部水深提供的概略深度计算地形概略梯度,并作为初始条件;
3) 借助式 (4) 所示反演模型,通过迭代进行地形反演;
4) 设定阈值ε,重复步骤1)~3),直至两次迭代地形差值满足式 (6).
5) 输出最终反演地形,并进行精度评估.
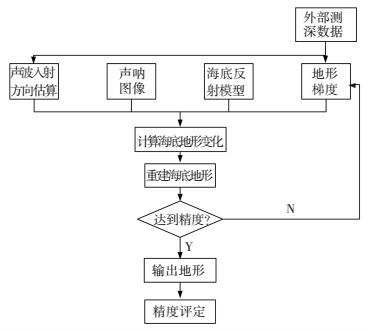
地形反演流程如图 2所示.
|
图 2 声呐图像反演海底地形流程图 Figure 2 The inversion process for obtaining seafloor from sonar images |
为评价反演方法的有效性,对反演结果进行精度评定.精度评定包括两部分:内符合检验和外符合检验.内、外符合检验方法分别以参与构建和未参与构建初始海底地形的实测水深数据为参考,利用式 (7),将对应位置的反演结果与之较差,计算较差结果的均值、最大值、最小值和均方根误差RRMSE,并绘制误差概率分布函数PDF (probability distribution function) 曲线.
| $ {R_{{\rm{RMSE}}}} = \sqrt {\frac{{\left[ {\Delta D\Delta D} \right]}}{n}} ,\Delta D = Z - {Z_{{\rm{real}}}}. $ | (7) |
式中ΔD是反演值Z与实测值Zreal间的差值.按照国际海道测量组织 (IHO) 的要求,当水深小于20 m时,最大测量误差不能超过20 cm.
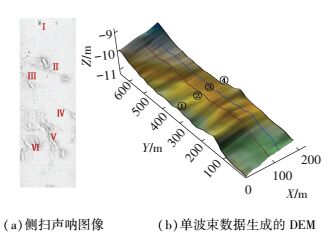
2 实验及分析为验证上述方法,在珠海水域开展了相关实验.测区范围约700 m×200 m;测区水深为9~12 m;测区底质特征基本相同,可视为同类底质.侧扫声呐测量采用Edgetech 4200,采样频率为400 kHz,横向分辨率为2 cm,纵向分辨率为0.5 m,水平波束宽度为0.3°,内置姿态传感器.外部测深数据通过单波束系统HY1600测量提供,工作频率为208 kHz,波束角为8°,测深精度为±(0.01 m+0.1% D).处理侧扫声呐的测量数据,得到像素分辨率为0.6 m的声呐图像如图 3(左) 所示,显著的地貌特征用Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ,Ⅵ标注.单波束系统在测线①②③④(图 3(右)) 上进行了测量,每条测线上测点间隔约为0.5 m.其中测线①—②、②—④ 间隔均约为100 m,测线②—③ 间隔约50 m.由图 3可以看出,单波束测深数据插值生成的海底地形图可以反映海底地形的整体变化趋势,但是不能反映高分辨率声呐图像上呈现的海底微特征.
|
图 3 同区域的侧扫声呐图像和地形图 Figure 3 The SSS image and the seafloor of the same area |
利用①、②、④ 三条测线测深数据内插得到初始地形,分别将顾及式 (4) 中的一阶项和二阶项作为反演模型进行地形反演,并对反演结果利用③ 测线中的测深数据进行精度评估.
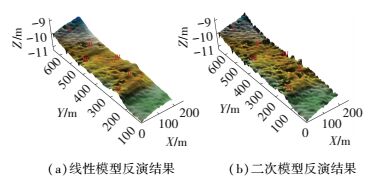
图 4给出了两种模型下的地形反演结果,可看出二者均较图 3(右) 实测地形精细,清晰地呈现出了SSS图像中的特征Ⅰ~Ⅵ. 图 4(右) 相较图 4(左),除反映显著特征外,还呈现出了微小的起伏,对地形的反映更细腻.分析认为,图 4(右) 基于顾及二阶项的反演模型反演结果,较单一顾及一阶项的反演模型的反演结果理论上更全面,更准确.
|
图 4 使用不同反演模型得到的海底地形 Figure 4 The seafloor produced by different inversion algorithms |
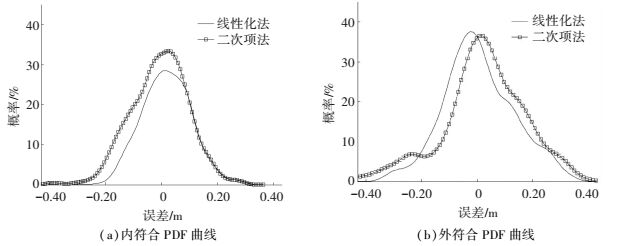
为了定量评估这两种模型反演结果的精度,用参与构建初始地形的测线测深数据与反演结果较差,统计分析其内符合精度;用测线③ 的测深数据与反演地形结果比较,并对偏差进行精度统计,分析其外符合精度.两种检验下的偏差统计参数见表 1,偏差的PDF曲线如图 5所示.可以看出,利用两种方法反演得到的结果内、外符合精度都服从正态分布,其中顾及一阶项模型所得结果内符合检验误差97%小于20 cm,最大为28 cm,均方根误差为9 cm;外符合检验则有88%小于20 cm,最大为38 cm,均方根误差为13 cm.顾及二次项反演模型所得结果的内符合检验误差有96%小于20 cm,最大为30 cm,均方根误差为10 cm;而外部检验误差80%小于20 cm,最大为43 cm,均方根误差为15 cm.
| 表 1 不同反演方法所得结果的内外符合误差统计参数 Table 1 Statistical parameters of biases produced by the linear and quadratic algorithm |
|
图 5 两种方法反演结果的误差概率分布曲线 Figure 5 PDF curves of the biases of different algorithms |
单纯比较统计量值,顾及一阶项模型略优于顾及二阶项模型,但也可以发现,这种优势非常微弱,偏差极值仅有1~6 cm,而均方根误差仅有1~2 cm.海洋环境复杂,无论是侧扫声呐成像还是单波束测深,测量误差远大于上述量级,因此可以认为上述误差由图像成像误差和测深误差引起,两种模型反演结果的精度基本一致.考虑模型的复杂程度以及计算的简便性,建议采用顾及一阶项的线性反演模型,即可达到较好的地形反演精度.
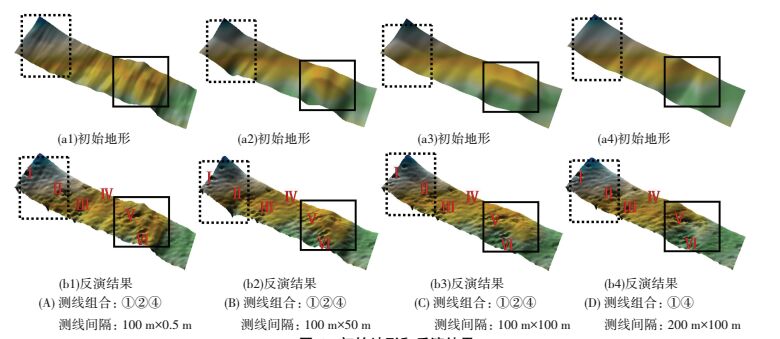
2.2 初始地形分辨率对反演结果的影响分别取不同测线组合构建初始地形,利用线性反演模型进行地形反演,并对反演结果进行精度评估. 图 6为基于不同测线测深数据组合形成的初始地形和反演地形,图 6(上) 为初始地形,图 6(下) 为反演地形.可以看出,反演地形较初始地形要精细,清晰地呈现出了图 3(左) 中的Ⅰ~Ⅵ特征的形状,而初始地形则难以呈现这些特征.
|
图 6 初始地形和反演结果 Figure 6 Initial seafloor and the inversion results |
但也可以发现,基于不同分辨率的初始地形所得的反演地形存在差异.对图 6(A)~(D)列中用虚线矩形和实线矩形框起来的区域进行对比,发现虚线矩形内地形变化比较平缓,实线矩形内地形起伏变化较大. 图 6(A)~(D)列中虚线矩形内地形趋势和微特征相一致;而实线矩形中的区域中 (A) 列的初始地形具有明显连贯的两个突起,随着构建初始地形的测深分辨率的降低,(B) 和 (C) 列矩形框部分变成一个整体的突起.而当初始地形分辨率进一步降低时,虽然 (D) 列初始地形整体趋势与 (A)、(B)、(C) 相同,但反演结果在实线矩形区则明显不同.这是由于初始地形为反演过程提供绝对基准和尺度约束,反演结果的整体趋势与初始地形一致,同时又可以呈现声呐图像上的微特征.当实际地形趋势变化较平滑时,测深数据密度的大小对反演结果影响不大;当实际地形趋势复杂时,少量测深数据生成的初始地形不能准确地反映实际地形变化,导致不同分辨率测深数据生成的初始地形会影响反演结果的地形特征.
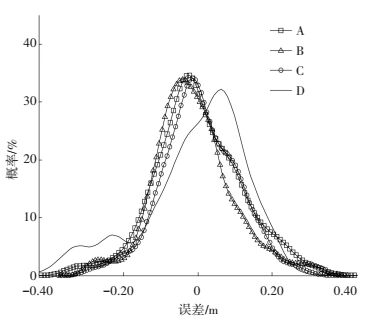
为了定量地评估初始地形分辨率对反演地形的影响,对图 6中整个区域在4个不同分辨率初始地形下的反演结果进行内外符合精度评估 (见表 2),反演结果偏差的PDF如图 7所示.可以看出 (A)~(C) 反演结果的外符合精度均满足正态分布,精度基本一致,即初始地形分辨率为100 m×100 m时即可实现高分辨率海底地形反演;(D) 反演结果存在系统偏差.分析认为随着初始地形分辨率的降低,初始地形已不能准确反映实际地形趋势,尽管基于图 2迭代过程对这种偏离具有一定的校正作用,但当偏差较大时,校正能力有限.为此在地形反演中,建议提供能够反映地形趋势、具有一定分辨率的测深数据.
| 表 2 不同初始地形所得结果的内外符合误差统计参数 Table 2 Statistical parameters of biasesof topographies inversed with different initial topographies |
|
图 7 不同分辨率初始地形反演结果误差的概率分布曲线 Figure 7 PDF curves of biases of topographies inversed with different initial topographies |
基于以上分析,选用100 m×100 m分辨率测深数据构建的海底地形作为初始地形,选用线性反演模型,基于图 3(左) 所示SSS图像,反演该水域的海底地形如图 6(C)所示.由于图像单个像素的实际尺寸为0.6 m,故反演地形分辨率相较初始地形提高了约170倍.
2.3 区域反演地形与实际地形的比较为分析区域反演结果与实际地形的一致性,基于以上讨论所得反演参数 (50 m测深分辨率,线性反演模型) 对540 m×165 m实验区域的侧扫声呐图像进行地形反演. 图 8给出了该区域的声呐图像、实际地形、50 m分辨率的均匀分布地形和代表性地形、反演地形.

|
图 8 均匀地形和代表性地形的反演结果 Figure 8 The inversion results of the different kinds of intial seafloor |
从图 8看出,声呐图像和实际地形中均存在明显突起特征 (如Ⅰ~Ⅳ),在这些特征处选择测深点 (图 8(d)所示代表性地形) 构建反演约束模型,反演地形如图 8(f)所示.相较用50 m×50 m均匀分布的测深数据 (图 8(c)所示地形) 作为约束获得的反演结果 (如图 8(e)),基于代表性测深数据反演的地形对特征描述的更精细、更准确,需要的测深数据量更少.
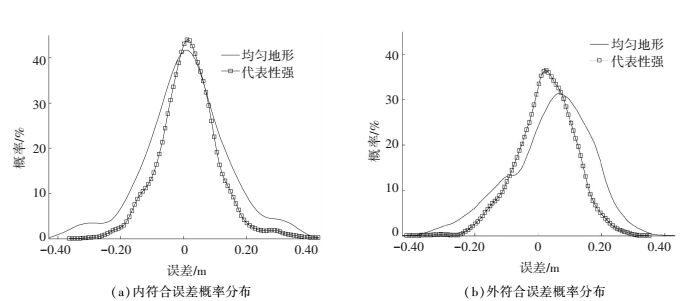
对两类测深数据约束下的反演结果进行精度评估,其内外符合检验的精度如表 3所示,PDF曲线如图 9所示.可以看出,统计结果进一步验证了上述结论,即代表性强的外部测深数据相较均匀分布的外部测深数据约束下的反演结果更能真实地反映海底的微地形,误差分布的聚敛性更好.但同时也看到,无论采用哪一类测深数据约束,反演地形与实际地形均取得了较好的一致性,地形反演精度均满足了测深精度要求,表明了本文提出的线性反演算法的正确性.
| 表 3 反演结果的内外符合检验误差统计参数 Table 3 Statistical parameters of biases of the inversed topographies |
|
图 9 不同初始地形约束条件下反演结果的误差概率分布曲线 Figure 9 PDF curves of the biases of the inversion results from different intial topographies |
1) 提出的基于侧扫声呐图像反演海底地形的线性算法,解决了现有测深方法获取高分辨率海底地形的难题,为高质量海底地形的获取提供了一种新的途径.该方法在实验中取得了均方根误差优于15 cm的海底地形反演精度,并将测深数据分辨率提高了170倍.
2) 高分辨率侧扫声呐图像为高分辨率地形反演提供了基础,但需要具有一定代表性、分辨率的外部测深数据为该反演提供基准和尺度约束.外部测深数据分辨率的选取应遵循对实际地形趋势能够真实反映的基本原则.地形变化平缓时,较低的测深分辨率即可满足需要,反之需要较高分辨率的测深数据.代表性强的外部测深数据,可以提高基准和尺度约束模型的精度,进而提高反演结果的精度.因此在选取外部测深数据时,除了顾及其分辨率外,还应考虑其代表性.
3) 理论上,反演结果还会受到海底不均匀底质因素的影响.文中的实验区域为近似同底质海底,由于影响一致,研究给出的线性反演算法取得了较好的反演结果.对于非均匀底质的情况,建议在实施海底地形反演之前,首先基于侧扫声呐图像进行海底监督 (具备海底底质采样数据) 和非监督分类,并据此对反射强度进行补偿,消除底质因素对回波强度的影响,借助仅反映海底地形起伏变化的回波强度进行海底地形反演,以提高海底地形反演精度.
| [1] |
陈江欣, 关永贤, 宋海斌, 等. 麻坑、泥火山在南海北部与西部陆缘的分布特征和地质意义[J].
地球物理学报, 2015, 58(3): 919-938.
CHEN Jianxin, GUAN Yongxian, SONG Haibin, et al. Distribution characteristics and geological implications of pockmarks and mud volcanoes in the northern and western continental margins of the South China Sea[J]. Chinese J. Geophys, 2015, 58(3): 919-938. DOI: 10.6038/cjg20150319 |
| [2] |
陈义兰, 刘乐军, 刘晓瑜, 等. 深海油气勘探中的海底地形勘测技术[J].
海洋测绘, 2015, 35(2): 18-22.
CHEN Yilan, LIU Lejun, LIU Xiaoyu, et al. Seabed topographic survey technology in deep-sea oil and gas exploration[J]. Hydrographic Surveying and Charting, 2015, 35(2): 18-22. |
| [3] | KAESER A J, LITTS T L, TRACY T. Using low-cost side-scan sonar for benthic mapping throughout the lower Flint River, Georgia, USA[J]. River Research and Applications, 2013, 29(5): 634-644. DOI: 10.1002/rra.v29.5 |
| [4] | POWERS J, BREWER S K, LONG J M, et al. Evaluating the use of side-scan sonar for detecting freshwater mussel beds in turbid river environments[J]. Hydrobiologia, 2015, 743(1): 127-137. DOI: 10.1007/s10750-014-2017-z |
| [5] | BLONDEL P. The Handbook of Side Scan Sonar[M]. UK: Springer Science & Business Media, 2010: 35-46. |
| [6] | YUILLE A L. The Lambertian Reflectance Model[R]. Los Angeles: University of California, 2012. |
| [7] |
廖熠, 赵荣椿. 从明暗恢复形状 (SFS) 的几类典型算法分析与评价[J].
中国图象图形学报 (A辑), 2001, 6(10): 953-961.
LIAO Yi, ZHAO Rongchun. Analysis and evaluation of several typical SFS algorithms[J]. Journal of Image and Graphics, 2001, 6(10): 953-961. |
| [8] | TANKUS A, SOCHEN N, YESHURUN Y. Shape-from-shading under perspective projection[J]. International Journal of Computer vision, 2005, 63(1): 21-43. DOI: 10.1007/s11263-005-4945-6 |
| [9] | PRADOS E. FAUGERAS O. Shape from shading: a well-posed problem[C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. San Diego: IEEE, 2005:870-877. |
| [10] | RAGHEB H, HANCOCK E R. Surface radiance correction for shape from shading[J]. Pattern Recognition, 2005, 38(10): 1574-1595. DOI: 10.1016/j.patcog.2005.03.025 |
| [11] | AHMED A H, FARAG A A. A flew formulation for shape from shading for non-lambertian surfaces[C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE Computer Society, 2006: 1817-1824. |
| [12] |
王国珲, 韩九强, 贾洪海, 等. 一种从明暗恢复形状的快速黏性解算法[J].
西安交通大学学报, 2009, 43(6): 43-47.
WANG Guohui, HAN Jiuqiang, JIA Honghai, et al. A fast viscosity solution algorithm for shape from shading[J]. Journal of Xi'An Jiaotong University, 2009, 43(6): 43-47. DOI: 10.7652/xjtuxb200906010 |
| [13] | AHMED A, FARAG A. Shape from shading for hybrid surfaces[C]// Proceedings of the IEEE International Conference on Image Processing. San Antonio: IEEE, 2007: 525-528. |
| [14] | DURA E, BELL J, LANE D. Reconstruction of textured seafloors from side-scan sonar images[J]. IET Radar, Sonar and Navigation, 2004, 151(2): 114-126. DOI: 10.1049/ip-rsn:20040262 |
| [15] | COIRAS E, PETILLOT Y, LANE D M. Multiresolution 3-D reconstruction from side-scan sonar images[J]. IEEE Transactions on Image Processing, 2007, 16(2): 382-390. DOI: 10.1109/TIP.2006.888337 |
| [16] | MOSZYNSKI M, BIKONIS K, LUBNIEWSKI Z. Reconstruction of 3D shape from sidescan sonar images using shape from shading technique[J]. Hydroacoustics, 2013, 16: 181-188. |
| [17] | BIKONIS K, MOSZYNSKI M, LUBNIEWSKI Z. Application of shape from shading technique for side scan sonar images[J]. Polish Maritime Research, 2013, 20(3): 39-44. |
 2017, Vol. 49
2017, Vol. 49


