无线通信中,由于信号传输的开放性,信息的安全传输是一个重要的问题.采用保密编码的加密技术是信息保密的传统技术,而近年来利用无线信道随机性的物理层安全方法正越来越受到关注.应用多天线技术实现信息的安全传输是物理层安全技术研究中的热点问题之一.文献[1]提出使用波束赋形的技术来实现物理层安全,中继和协作干扰技术也是提高无线通信保密传输性能的有效手段[2-4].
空间调制SM (spatial modulation) 技术[5]是一种多天线传输技术,通过不同收发天线间信道特性的差异来传递消息.在SM的调制器中, 比特信息分为两部分:一部分在信号域进行传统的幅相调制APM (amplitude and phase modulation); 另一部分在空间域进行调制,选择性地激活一根天线来传输信号.广义空间调制GSM (generalized spatial modulation) 技术[6]则对发射天线进行不同组合,每次由多根激活天线发送信号.相比较SM系统,GSM系统具有更高的频谱效率,但系统复杂度也更高. SM和GSM系统中,只同时激活部分天线,发射机需要的射频单元数量少于传统的多天线系统,在射频部分具有更高的能量效率[7].文献[8-10]讨论了GSM信号的检测方法,文献[11]分析了GSM系统的互信息,并对系统误码性能进行了分析.目前,有少量的文献对空间调制技术在保密传输中的应用进行了研究.文献[12]假设发送端能获得窃听者信道状态信息CSI (channel state information),对SM系统的误码率和保密互信息进行了推导,提出在发射端对信息进行预处理,可使合法接收者能正常进行SM调制信号的解调,但窃听者不能区分发送天线,无法解调映射到天线索引上的信息.文献[13]采用接收天线索引来表示信息,通过合理设计发送端的预处理向量,可使接收端能够判断哪根接收天线上有接收信号,从而根据接收天线索引获得发送的信息,而窃听者不能区分,这样能获得一定的保密传输速率.
本文研究多发送天线系统中应用GSM技术实现信息的保密传输.系统中的发射端在发送空间调制后的信号前进行预处理,使各激活天线发送的信号到达合法接收者天线时具有相同的相位,增强接收信号信噪比,同时使合法接收者处的空间星座点等相位间隔分布,降低误码率.而各激活天线发送的信号到达窃听者接收天线时的相位是随机的,其空间调制部分的解调误码率远高于合法接收者,有效保护通过天线索引部分携带的信息.
1 系统模型系统模型如图 1所示,包括3个节点,其中Alice为装备Nt根天线的发送端,向两个单天线节点发送信息.两个单天线节点都是系统的用户,但发送给其中一个节点的信息需要对另一个节点保密.不失一般性,称某时刻接收保密信息的节点为合法接收者Bob,而另一个节点称为窃听者Eve.记每传输时隙Alice的发射信号为X,Hb∈
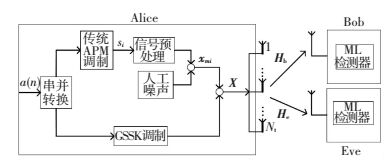
|
图 1 GSM安全传输系统模型 Figure 1 Model of secure transmission system with GSM |
每传输时隙,Alice将B比特的信息序列a (n)分成B1比特和B2比特两部分,B=B1+B2.每组数据的前B1比特用来选择所有发射天线组合2B1中的一种,激活天线组合的数目为Nc=2B1,其中B1=
经过信道传输后,Bob和Eve接收到信号为
| $ \left\{ \begin{array}{l} {y_{\rm{b}}} = {\mathit{\boldsymbol{H}}_{{\rm{b}}m}}\mathit{\boldsymbol{X + }}{n_{\rm{b}}} = \sum\limits_{k = 1}^{{N_{\rm{a}}}} {\left( {{h_{{\rm{b}}m,k}}{x_{mi,k}}} \right) + {n_{\rm{b}}} = {\mathit{\boldsymbol{h}}_{{\rm{b}}m}}{\mathit{\boldsymbol{x}}_{mi}} + {n_{\rm{b}}}} ,\\ {y_{\rm{e}}} = {\mathit{\boldsymbol{H}}_{{\rm{e}}m}}\mathit{\boldsymbol{X + }}{n_{\rm{e}}} = \sum\limits_{k = 1}^{{N_{\rm{a}}}} {\left( {{h_{{\rm{e}}m,k}}{x_{mi,k}}} \right) + {n_{\rm{e}}} = {\mathit{\boldsymbol{h}}_{{\rm{e}}m}}{\mathit{\boldsymbol{x}}_{mi}} + {n_{\rm{e}}}} . \end{array} \right. $ | (1) |
式中:hbm=[hbm, 1, hbm, 2, …, hbm, Na]、hem=[hem, 1, hem, 2, …, hem, Na]分别表示Alice的激活天线与Bob、Eve接收天线间的信道系数向量,对于瑞利衰落信道,其元素为服从独立同分布的复高斯随机变量;nb、ne是均值为0,方差为σb2、σe2的复高斯白噪声.将xmi=wmsi+n代入 (1),接收信号可进一步表示为
| $ \begin{array}{l} {y_{\rm{b}}} = {\mathit{\boldsymbol{h}}_{{\rm{b}}m}}\left( {{\mathit{\boldsymbol{w}}_m}{s_i} + \mathit{\boldsymbol{n}}} \right) + {n_{\rm{b}}} = {\mathit{\boldsymbol{h}}_{{\rm{b}}m}}{\mathit{\boldsymbol{w}}_m}{s_i} + {\mathit{\boldsymbol{h}}_{{\rm{b}}m}}{\mathit{\boldsymbol{g}}_m}z + {n_{\rm{b}}},\\ {y_{\rm{e}}} = {\mathit{\boldsymbol{h}}_{{\rm{e}}m}}\left( {{\mathit{\boldsymbol{w}}_m}{s_i} + \mathit{\boldsymbol{n}}} \right) + {n_{\rm{e}}} = {\mathit{\boldsymbol{h}}_{{\rm{e}}m}}{\mathit{\boldsymbol{w}}_m}{s_i} + {\mathit{\boldsymbol{h}}_{{\rm{e}}m}}{\mathit{\boldsymbol{g}}_m}z + {n_{\rm{e}}}. \end{array} $ | (2) |
预处理向量wm设计的目标是使各激活天线发射的承载信息的幅相调制符号si到达Bob的接收天线时在相位上是对齐的,同时使不同激活天线组合的合成信号相位在相邻的APM调制符号的相位间隔范围内是等相位间隔分布的. 图 2给出了Nt=4、Na=2,采用QPSK调制时,发送信号的预处理过程示意图,图中表示的都是无噪声情况下的信号. 图 2(a)表示Alice未对信号进行预处理时,到达Bob接收天线的两个信号及其合成信号的示意图,si为APM调制符号,这里假设其相位为0,(hbm, 1+hbm, 2)si为合成信号.由于信道的随机性,两个激活天线发射的信号在达到Bob接收天线时相互叠加的结果有可能使信号增强,也可能使信号减弱. 图 2(b)中,Alice根据信道的特性对发送信号用因子e-jθk进行预加权,使各激活天线发送的信号到达Bob接收天线时相位都对齐到0相位,增强接收信号. 图 2(c)是Alice对信号进行相位对齐预处理后Bob接收信号的星座图,同相和正交轴上的4组信号点分别对应QPSK的4种符号.为了增大同一个APM符号下不同激活天线组合对应信号点间的距离,Alice在发送信号上进一步附加一个不同相位偏移,使这些信号点在相位相邻的两个APM符号间等相位间隔分布,如图 2(d)所示.对于幅相调制采用QPSK的情形,对激活天线组合m附加的相位偏移为θm=(m-1)π/8.
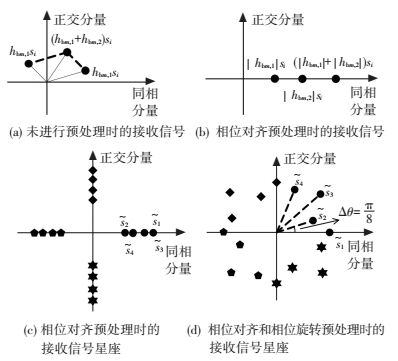
|
图 2 信号预处理过程示意 Figure 2 Diagram of signal pretreatment |
由上述分析可得,向量wm为
| $ {\mathit{\boldsymbol{w}}_m} = \sqrt {{P_{\rm{s}}}} \mathit{\boldsymbol{A}}{{\rm{e}}^{{\rm{j}}{\theta _m}}},\mathit{\boldsymbol{A = }}{\left[ {{{\rm{e}}^{ - {\rm{j}}{\theta _1}}}\;{{\rm{e}}^{ - {\rm{j}}{\theta _2}}} \cdots {{\rm{e}}^{ - {\rm{j}}{\theta _{{N_{\rm{a}}}}}}}} \right]^{\rm{T}}}. $ | (3) |
式中: Ps为发射信号的功率;A使各激活天线发射的信号在到达Bob时相位对齐;θm是相位旋转因子,θm=(m-1)Δφ/Nc,其中Δφ是APM星座中星座点间的最小相位间隔,对于MPSK,Δφ=2π/M.
人工噪声n应尽可能不对Bob的接收产生影响,理想情况下应满足hbmgm=0,同时应该对窃听者产生最大的干扰.人工噪声波束赋形矢量的设计可表示为优化问题:
| $ \begin{array}{*{20}{c}} {\mathop {\max }\limits_{{g_m}} {{\left| {{\mathit{\boldsymbol{h}}_{{\rm{e}}m}}{\mathit{\boldsymbol{g}}_m}} \right|}^2},}\\ {{\rm{s}}{\rm{.t}}{\rm{.}}\;{\mathit{\boldsymbol{h}}_{{\rm{b}}m}}{\mathit{\boldsymbol{g}}_m} = 0,\;{\rm{tr}}\left( {{\mathit{\boldsymbol{g}}_m}\mathit{\boldsymbol{g}}_m^{\rm{H}}} \right) = {P_n}.} \end{array} $ |
式中:上标H表示共轭转置,Pn为发送人工噪声的功率,|·|表示求模,tr (·) 表示矩阵的迹.约束条件hbmgm=0表示人工噪声对合法接收者不产生影响.
设U⊥为信道hbm零空间的投影矩阵,hbmU⊥=0,由文献[14]可知U⊥=INa-hbmH(hbmhbmH)-1hbm.得到U⊥后,可设gm=U⊥g′m,为使|hemgm|2=|hemU⊥gm′|2最大化,只需g′m与hemU⊥共线,故g′m=aU⊥HhemH,其中a为实系数.可设a=1,则g′m=U⊥HhemH,那么gm=U⊥U⊥HhemH.由U⊥的表达式有U⊥=U⊥H和U⊥U⊥=U⊥,所以gm=U⊥hemH.在满足人工噪声功率约束条件tr (gmgmH)=Pn时,最优波束赋形矢量为gm=
| $ \mathit{\boldsymbol{n}} = {\mathit{\boldsymbol{g}}_m}z = \sqrt {{P_{\rm{n}}}} {\mathit{\boldsymbol{R}}_m}z. $ | (4) |
将式 (3) 和式 (4) 代入式 (2) 中,Bob和Eve的接收信号可表示为
| $ \begin{array}{l} {y_{\rm{b}}} = {\mathit{\boldsymbol{h}}_{{\rm{b}}m}}\sqrt {{P_{\rm{s}}}} \mathit{\boldsymbol{A}}{{\rm{e}}^{{\rm{j}}{\theta _m}}}{s_i} + {\mathit{\boldsymbol{h}}_{{\rm{b}}m}}\sqrt {{P_{\rm{n}}}} {\mathit{\boldsymbol{R}}_m}z + {n_{\rm{b}}} = \\ \;\;\;\;\;\;\;\sqrt {{P_{\rm{s}}}} {c_{\rm{m}}}{s_i} + {n_{\rm{b}}},\\ {y_{\rm{e}}} = {\mathit{\boldsymbol{h}}_{{\rm{e}}m}}\sqrt {{P_{\rm{s}}}} \mathit{\boldsymbol{A}}{{\rm{e}}^{{\rm{j}}{\theta _m}}}{s_i} + {\mathit{\boldsymbol{h}}_{{\rm{e}}m}}\sqrt {{P_{\rm{n}}}} {\mathit{\boldsymbol{R}}_m}z + {n_{\rm{e}}} = \\ \;\;\;\;\;\;\;\sqrt {{P_{\rm{s}}}} {c_{\rm{m}}}{s_i} + \sqrt {{P_{\rm{n}}}} {\mathit{\boldsymbol{h}}_{{\rm{e}}m}}{\mathit{\boldsymbol{R}}_m}z + {n_{\rm{e}}}. \end{array} $ |
式中,cm=
需要说明的是,实现人工噪声不对合法接收者的接收产生影响,同时对窃听者的干扰最大化的前提是能获得合法信道和窃听信道准确的CSI.如果该条件不满足,则人工噪声会对合法接收者的接收会有一定的影响.
Bob对接收信号的幅相调制和空间调制采用最大似然ML (maximum-likelihood) 准则联合检测:
| $ \left[ {\hat m,{{\hat s}_i}} \right] = \arg \mathop {\min }\limits_{\begin{array}{*{20}{c}} {m \in \left\{ {1,2, \cdots ,{N_c}} \right\}}\\ {i \in \left\{ {1,2, \cdots ,M} \right\}} \end{array}} \left\{ {{{\left\| {{y_{\rm{b}}} - \sqrt {{P_{\rm{s}}}} {c_{\rm{m}}}{s_i}} \right\|}^2}} \right\}. $ |
Eve对接收信号的幅相调制和空间调制也进行ML准则联合检测:
| $ \left[ {\hat m,{{\hat s}_i}} \right] = \arg \mathop {\min }\limits_{\begin{array}{*{20}{c}} {m \in \left\{ {1,2, \cdots ,{N_c}} \right\}}\\ {i \in \left\{ {1,2, \cdots ,M} \right\}} \end{array}} \left\{ {{{\left\| {{y_{\rm{e}}} - \sqrt {{P_{\rm{s}}}} {d_{\rm{m}}}{s_i}} \right\|}^2}} \right\}. $ |
保密容量是系统可以达到的最大保密传输速率,是反映系统性能一个极限值.发射端的发射功率分为两部分,一部分用于发射承载信息的信号,另一部分发射人工噪声.假设总发射功率为P,功率分配因子为ρ,发射信号的功率为Ps=E[‖wmsi‖2]=ρP,而发射人工噪声的功率为Pn=E[nHn]=(1-ρ)P.由于GSM信号包含发射天线索引信息和APM调制信息两部分,所以接收信号与发送信号间的互信息也由两部分组成.采用与文献[7]求GSM信道容量方法,可得Bob和Eve的瞬时信道容量分别为
| $ \begin{array}{l} {C_{\rm{b}}} = {\log _2}\left( {1 + \frac{{{P_{\rm{s}}}}}{{{N_{\rm{a}}}{N_{\rm{c}}}\sigma _{\rm{b}}^2}}{\mathit{\boldsymbol{H}}_{\rm{b}}}\mathit{\boldsymbol{GH}}_{\rm{b}}^{\rm{H}}} \right),\\ {C_{\rm{e}}} = {\log _2}\left( {1 + \frac{P}{{{N_{\rm{a}}}{N_{\rm{c}}}\left( {{P_{\rm{n}}}{\mathit{\boldsymbol{h}}_{{\rm{e}}m}}{\mathit{\boldsymbol{R}}_m}\mathit{\boldsymbol{R}}_m^{\rm{H}}\mathit{\boldsymbol{h}}_{{\rm{e}}m}^{\rm{H}}} \right) + \sigma _{\rm{e}}^2}}{\mathit{\boldsymbol{H}}_{\rm{e}}}\mathit{\boldsymbol{GH}}_{\rm{e}}^{\rm{H}}} \right). \end{array} $ |
式中,G表示在所有激活天线组合中,各天线被使用的次数所组成的对角矩阵.如当Nt=4,Na=2时,Nc=4,选择6个组合中的4组激活天线组合,分别为 (1, 2)、(1, 3)、(1, 4)、(2, 3),天线1使用3次,天线2使用2次,天线3使用2次,天线4使用1次,故G=diag (3, 2, 2, 1).瞬时保密容量为
| $ \begin{array}{l} {C_{\rm{s}}} = {\left[ {{C_{\rm{b}}} - {C_{\rm{e}}}} \right]^ + } = \left[ {{{\log }_2}\left( {1 + \frac{{\rho P}}{{{N_{\rm{a}}}{N_{\rm{c}}}\sigma _{\rm{b}}^2}}{\mathit{\boldsymbol{H}}_{\rm{b}}}\mathit{\boldsymbol{GH}}_{\rm{b}}^{\rm{H}}} \right) - } \right.\\ {\left. {{{\log }_2}\left( {1 + \frac{{\rho P}}{{{N_{\rm{a}}}{N_{\rm{c}}}\left( {\left( {1 - \rho } \right)P{\mathit{\boldsymbol{h}}_{{\rm{e}}m}}{\mathit{\boldsymbol{R}}_m}\mathit{\boldsymbol{R}}_m^{\rm{H}}\mathit{\boldsymbol{h}}_{{\rm{e}}m}^{\rm{H}} + \sigma _{\rm{e}}^2} \right)}}{\mathit{\boldsymbol{H}}_{\rm{e}}}\mathit{\boldsymbol{GH}}_{\rm{e}}^{\rm{H}}} \right)} \right]^ + }. \end{array} $ | (5) |
式中[α]+=max{0, α},即保密容量Cs取值大于0或等于0.保密容量是ρ的函数,但不是ρ的单调函数,存在一个最优的ρ值使系统的保密容量最大.
记a1=HbGHbH,a2=HeGHeH,a3=σb2,a4=σe2,a5=NaNc,a6=hemRmRmHhemH,式 (5) 可简记为
| $ {C_{\rm{s}}} = {\left[ {{{\log }_2}\left( {1 + \frac{{{a_1}P\rho }}{{{a_3}{a_5}}}} \right) - {{\log }_2}\left( {1 + \frac{{{a_2}P\rho }}{{{a_5}\left( {{a_6}P\left( {1 - \rho } \right) + {a_4}} \right)}}} \right)} \right]^ + }. $ |
对每传输时隙而言,信道系数Hb、He、hb、he为定值,那么a1~a6的值都是确定的.令
| $ f\left( \rho \right) = {\log _2}\left( {1 + \frac{{{a_1}P\rho }}{{{a_3}{a_5}}}} \right) - {\log _2}\left( {1 + \frac{{{a_2}P\rho }}{{{a_5}\left( {{a_6}P\left( {1 - \rho } \right) + {a_4}} \right)}}} \right), $ | (6) |
式 (6) 是ρ的连续函数,最优的功率分配因子ρ值就是在[0, 1]间使f(ρ) 最大的值,最大值点可能是f(ρ) 函数一阶导数为零时在[0, 1]之间的解,也可能是0、1边界点. f(ρ) 的一阶导数为
| $ \begin{array}{*{20}{c}} {\frac{{{\rm{d}}f\left( \rho \right)}}{{{\rm{d}}\rho }} = \frac{1}{{\ln 2}}\left( {\frac{{{a_1}P\left( {{a_4}{a_5} + {a_5}{a_6}P + {a_2}P\rho - {a_5}{a_6}P\rho } \right)\left( {{a_4}{a_5} + {a_5}{a_6}P - {a_5}{a_6}P\rho } \right)}}{{\left( {{a_1}P\rho + {a_3}{a_5}} \right)\left( {{a_4}{a_5} + {a_5}{a_6}P + {a_2}P\rho - {a_5}{a_6}P\rho } \right)\left( {{a_4}{a_5} + {a_5}{a_6}P - {a_5}{a_6}P\rho } \right)}} - } \right.}\\ {\left. {\frac{{\left( {{a_1}P\rho + {a_3}{a_5}} \right)\left( {{a_2}{a_4}{a_5}P + {a_2}{a_4}{a_6}{P^2}} \right)}}{{\left( {{a_1}P\rho + {a_3}{a_5}} \right)\left( {{a_4}{a_5} + {a_5}{a_6}P + {a_2}P\rho - {a_5}{a_6}P\rho } \right)\left( {{a_4}{a_5} + {a_5}{a_6}P - {a_5}{a_6}P\rho } \right)}}} \right).} \end{array} $ | (7) |
式 (7) 为零的解,就是其分子为零的解:
| $ \begin{array}{l} {a_1}P\left( {{a_4}{a_5} + {a_5}{a_6}P + {a_2}P\rho - {a_5}{a_6}P\rho } \right)\left( {{a_4}{a_5} + {a_5}{a_6}P - {a_5}{a_6}P\rho } \right) - \\ \left( {{a_1}P\rho + {a_3}{a_5}} \right)\left( {{a_2}{a_4}{a_5}P + {a_2}{a_4}{a_6}{P^2}} \right) = 0, \end{array} $ | (8) |
式 (8) 为一元二次方程,其解为
| $ \rho = \frac{{{a_1}{a_4}{a_5}{a_6} + {a_1}{a_5}a_6^2P \pm \sqrt {{a_1}{a_2}{a_5}{a_6}\left( {{a_4} + {a_6}P} \right)\left( {{a_1}{a_4} - {a_2}{a_3} + {a_3}{a_5}{a_6} + {a_1}{a_6}P} \right)} }}{{{a_1}{a_5}a_6^2P - {a_1}{a_2}{a_6}P}}. $ | (9) |
式 (9) 在[0, 1]内的那个解为极值点,其所对应的保密容量与边界点0和1对应的保密容量中的最大值即为该信道条件下最大保密容量.每次传输时最优的功率分配因子与最大保密容量对应.
3.2 误码性能分析保密容量是衡量系统保密传输能力的理论极限值,系统要获得达到保密容量的保密传输速率,要求发送的信号必须为高斯分布的信号,这在实际应用中是不可能的.实际系统中采用的是有限阶数的数字调制信号,此时可通过比较合法接收者和窃听者间的误码性能差距来衡量系统的保密传输能力.窃听者的误码率越高于合法接收者,系统的保密传输能力越高.由于精确的误码率难以获得,这里通过求Bob和Eve的成对差错概率Pr (xmi→xlj) 来获得平均误比特率P(s, m)的联合上界.
P(s,m) 的表达式为
| $ \begin{array}{l} {P_{\left( {s,m} \right)}} \le \frac{1}{{{N_{\rm{c}}}M{{\log }_2}\left( {{N_{\rm{c}}}M} \right)}}\mathop \Sigma \limits_{m = 1}^{{N_{\rm{c}}}} \mathop \Sigma \limits_{i = 1}^M \mathop {\mathop \Sigma \limits_{m = 1}^{{N_{\rm{c}}}} \mathop \Sigma \limits_{i = 1}^M }\limits_{\left( {l,j} \right) \ne \left( {m,i} \right)} d\left( {{\mathit{\boldsymbol{x}}_{mi}},{\mathit{\boldsymbol{x}}_{ij}}} \right).\\ \;\;\;\;\;\;\;\;\;\;E\left[ {\Pr \left( {{\mathit{\boldsymbol{x}}_{mi}} \to {\mathit{\boldsymbol{x}}_{ij}}} \right)} \right]. \end{array} $ | (10) |
式中: Pr (xmi→xlj) 表示将幅相调制符号si、激活天线组合为m错判成幅相调制符号sj、激活天线组合为l的成对差错概率;
对于Bob,其Pr (xmi→xlj) 为
| $ \begin{array}{l} \Pr \left( {{\mathit{\boldsymbol{x}}_{mi}} \to {\mathit{\boldsymbol{x}}_{ij}}} \right) = \Pr \left( {{{\left\| {{y_{\rm{b}}} - \sqrt {{P_{\rm{s}}}} {c_{\rm{m}}}{s_i}} \right\|}^2} > \left\| {{y_{\rm{b}}} - } \right.} \right.\\ \;\;\;\;\left. {{{\left. {\sqrt {{P_{\rm{s}}}} {c_l}{s_j}} \right\|}^2}} \right) = \Pr \left( {{P_{\rm{s}}}{{\left| {{c_m}} \right|}^2}{{\left| {{s_i}} \right|}^2} - } \right.\\ \;\;\;\;2{\mathop{\rm Re}\nolimits} \left( {y_{\rm{b}}^ * \sqrt {{P_{\rm{s}}}} {c_{\rm{m}}}{s_i}} \right) > {P_{\rm{s}}}{\left| {{c_l}} \right|^2}{\left| {{s_j}} \right|^2} - \\ \;\;\;\;\left. {2{\mathop{\rm Re}\nolimits} \left( {y_{\rm{b}}^ * \sqrt {{P_{\rm{s}}}} {c_l}{s_j}} \right)} \right) = \Pr \left( {{\mathop{\rm Re}\nolimits} \left( {{n_{\rm{b}}}\sqrt {{P_{\rm{s}}}} c_l^ * s_j^ * } \right) - } \right.\\ \;\;\;\;\left. {{\mathop{\rm Re}\nolimits} \left( {{n_{\rm{b}}}\sqrt {{P_{\rm{s}}}} c_m^ * s_i^ * } \right) > {P_{\rm{s}}}{{\left| {{c_m}{s_i} - {c_l}{s_j}} \right|}^2}/2} \right). \end{array} $ |
其中上标*表示取共轭.上式最后一行中,大于号的左边为服从均值为0,方差为Ps|cmsi-clsj|2σb2/2的高斯随机变量.成对差错概率为
| $ \Pr \left( {{\mathit{\boldsymbol{x}}_{mi}} \to {\mathit{\boldsymbol{x}}_{ij}}} \right) = Q\left( {\sqrt {\frac{{{P_{\rm{s}}}{{\left| {{c_m}{s_i} - {c_l}{s_j}} \right|}^2}}}{{2\sigma _{\rm{b}}^2}}} } \right), $ |
代入式 (10) 得Bob的误比特率为
| $ \begin{array}{l} {P_{\left( {s,m} \right),{\rm{b}}}} \le \frac{1}{{{N_{\rm{c}}}M{{\log }_2}\left( {{N_{\rm{c}}}M} \right)}}\mathop \Sigma \limits_{m = 1}^{{N_{\rm{c}}}} \mathop \Sigma \limits_{i = 1}^M \mathop {\mathop \Sigma \limits_{m = 1}^{{N_{\rm{c}}}} \mathop \Sigma \limits_{i = 1}^M }\limits_{\left( {l,j} \right) \ne \left( {m,i} \right)} .\\ \;\;\;\;\;\;\;\;\;\;\;\;d\left( {{\mathit{\boldsymbol{x}}_{mi}},{\mathit{\boldsymbol{x}}_{ij}}} \right)E\left[ {Q\left( {\sqrt {\frac{{{P_{\rm{s}}}{{\left| {{c_m}{s_i} - {c_l}{s_j}} \right|}^2}}}{{2\sigma _{\rm{b}}^2}}} } \right)} \right]. \end{array} $ |
在瑞利衰落信道下,采用文献[15]的方法对期望运算进行推导,最后可得
| $ \begin{array}{*{20}{c}} {{P_{\left( {s,m} \right),{\rm{b}}}} \le \frac{1}{{2M{{\log }_2}\left( {{N_{\rm{c}}}M} \right)}}\mathop \Sigma \limits_{i = 1}^M \mathop {\mathop \Sigma \limits_{i = 1}^M }\limits_{j \ne i} \left\{ {\left[ {\frac{{N_{\rm{c}}^2{{\log }_2}\left( {{N_{\rm{c}}}} \right)}}{2} + } \right.} \right.}\\ {\left. {{N_{\rm{c}}}\left( {{N_{\rm{c}}} - 1} \right)d\left( {{x_i},{x_j}} \right)} \right]\left. {\left( {1 - \sqrt {\frac{{\sigma _{1{\rm{b}}}^2}}{{1 + \sigma _{1{\rm{b}}}^2}}} } \right)} \right\}.} \end{array} $ |
式中σ1b2=σbh2γb(|si|2+|sj|2),γb=Ps/4σb2,σbh2表示Alice与Bob间信道系数方差.
对Eve而言,将其接收信号ye中的人工噪声和信道噪声一起记为nea=
| $ {y_{\rm{e}}} = \sqrt {{P_{\rm{s}}}} {d_m}{s_i} + {n_{{\rm{ea}}}}. $ |
与Bob误比特率的推导过程类似,可以推导得到Eve的误比特率为
| $ \begin{array}{l} {P_{\left( {s,m} \right),{\rm{e}}}} \le \frac{1}{{2M{{\log }_2}\left( {{N_{\rm{c}}}M} \right)}}\mathop \Sigma \limits_{i = 1}^M \mathop {\mathop \Sigma \limits_{i = 1}^M }\limits_{j \ne i} \left\{ {\left[ {\frac{{N_{\rm{t}}^2{{\log }_2}\left( {{N_{\rm{t}}}} \right)}}{2} + } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {{N_{\rm{t}}}\left( {{N_{\rm{t}}} - 1} \right)d\left( {{\mathit{\boldsymbol{x}}_i},{\mathit{\boldsymbol{x}}_j}} \right)} \right]\left. {\left( {1 - \sqrt {\frac{{\sigma _{1{\rm{e}}}^2}}{{1 + \sigma _{1{\rm{e}}}^2}}} } \right)} \right\}. \end{array} $ |
式中σ1e2=σeh2γe(|si|2+|sj|2),γe=Ps/4σnea2,σeh2表示Alice与Eve间信道系数方差.
4 仿真分析仿真中信道为相互独立的瑞利平坦衰落信道,信道衰落由大尺度衰落和小尺度衰落组成.假设所有信道的大尺度衰落因子均为-120 dB = 10-12,小尺度衰落因子为均值为0、方差为1的复高斯随机变量,这样所有信道的信道系数的方差均为10-12.假设所有信道噪声方差均为-120 dBm.本节所给出的仿真结果是信道变化5×105次所得结果的平均值.
图 3给出系统发送天线数Nt=4, 在不同功率分配因子ρ值下的保密容量,其中图 3(a)为激活天线数Na=2时的值,图 3(b)为Na=3时的值.可看到采用最优功率分配因子比采用其他功率分配因子时,系统的保密容量更大,具有更好的保密传输能力.
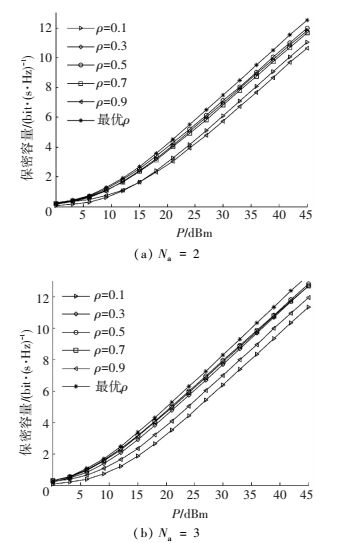
|
图 3 不同ρ时系统保密容量随P变化的情况,Nt=4 Figure 3 Security capacities with different ρ and P, Nt=4 |
图 4为本文方案在Nt=4、Na=2时,幅相调制采用QPSK调制,不同ρ值下Bob和Eve的误比特率随发送总功率P的变化曲线. 图 4中实线为仿真值,虚线为理论上界值.可以看到, 对同一P值,功率分配因子ρ越大,发射有用信号的功率越大,而发射人工噪声的功率越小,对于Bob和Eve而言都是误码率越低.但不管ρ如何取值,Bob的误码率都要优于Eve的误码率.而二者的误码率差距越大,系统的保密通信能力越强.
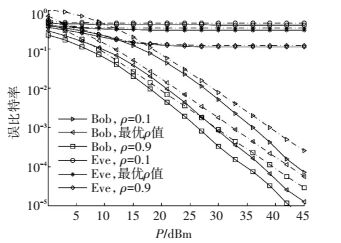
|
图 4 不同ρ时Bob和Eve的误比特率随P变化的情况,Nt=4,Na=2 Figure 4 Bit error rates of Bob and Eve with different ρ and P, Nt=4, Na=2 |
图 5给出了Nt=4、Na=2,幅相调制采用BPSK和QPSK调制,对激活天线发送信号是否进行相位旋转时,系统的误码性能随发送总功率P变化的仿真结果.从图 5可以看到,不论是采用BPSK还是QPSK调制,进行了相位旋转处理后,Bob的误码性能有明显的改善,而Eve的误码率则无明显的变化.
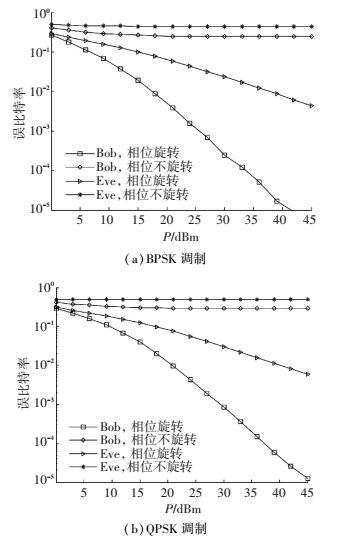
|
图 5 是否进行相位旋转的误比特率比较,Nt=4,Na=2 Figure 5 Bit error rates with and without phase shift, Nt=4, Na=2 |
图 6为本文方案与文献[12]方案中Bob和Eve误码性能和保密互信息的仿真对比,保密互信息 (即合法接收端从每个接收符号中获得的保密信息量) 采用文献[12]方法计算.文献[12]的SM系统中,在发送端已知所有信道CSI的条件下,发射端根据窃听信道的CSI,对发送信号进行预处理,使各发送天线与窃听者接收天线间的等效信道特性相同,使窃听者不能分辨发送的天线,无法解调映射到天线索引上的信息.这样的预处理对合法接收者则无影响.仿真中,本文方案和文献[12]方案的发送天线数都是Nt=4,幅相调制都采用QPSK.本文方案中每次激活的发送天线数为Na=3或Na=2,文献[12]方案中Na=1.两方案通过天线索引和幅相调制部分携带的信息量都相同,系统的频谱效率都是4 bit/symbol.从图 6(a)可看出本文方案和文献[12]方案中Eve的误比特率基本一致.但对Bob而言,本文方案的误比特率要远低于文献[12]的方案.从图 6(b)可看到本文方案保密互信息高于文献[12],也就意味着系统具有更好的保密传输能力,且激活天线数越多保密互信息越大.本文方案中,每次传输时激活的天线数越多,Bob的误码性能越好,因为激活天线数越多也就意味着发射分集更大,接收端性能更好.但相应的射频部分的复杂度也会增加,所以在实际选择时,需要考虑到性能和复杂度的均衡.
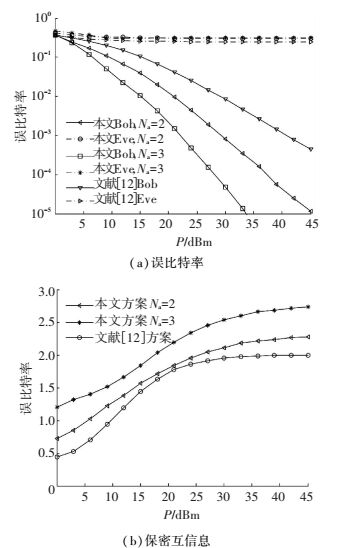
|
图 6 本文方案与文献[12]方案误码性能和保密互信息对比 Figure 6 Comparison of bit error rates and security mutual information between the schemes of this paper and Ref.[12] |
本文给出了在多发射天线系统中利用GSM调制技术的物理层安全传输方案, 系统通过发射天线索引和传统幅相调制符号传递信息.发送端利用其与合法接收者间的信道特性对发送信号进行预处理,使合法接收者接收到的来自各激活天线信号的相位对齐,获得发送分集的效果,增加信噪比.同时预处理过程还使各激活天线组合的合成信号相位等间隔分布,进一步提高合法接收者的接收性能,降低误码率.而窃听者接收到的来自各激活天线的信号相位仍为随机分布,无分集和相位等间隔分布的效果.为了防止窃听者获得幅相调制符号携带的信息,方案中还引入了指向窃听者的人工噪声.理论分析和仿真结果表明, 合法接收者的误码性能远优于窃听者,能获得可观的系统保密容量.本文中假设发射端能获得信道准确的CSI,在CSI存在误差的情况下,发送信号预处理向量和人工噪声的指向准确性都会有所下降,使系统的保密传输性能有所下降.研究在CSI有误差情况下具有良好鲁棒性的信号预处理和人工噪声方案将是下一步的研究问题.
| [1] | ZHANG Junwei, GURSOY M C. Relay beamforming strategies for physical-layer security[C]// Proceeding of 44th Annual Conference on Information Sciences and Systems. Piscataway: IEEE Press, 2010: 1-6. DOI: 10.1109/CISS.2010.5464970. |
| [2] | LIU Yupeng, LI Jiangyuan, PETROPULU A P. Destination assisted cooperative jamming for wireless physical-layer security[J]. IEEE Transactions on Information Forensics and Security, 2013, 8(4): 682-694. DOI: 10.1109/TIFS.2013.2248730 |
| [3] | ZOU Yulong, WANG Xianbin, SHEN Weiming. Optimal relay selection for physical layer security in cooperative wireless networks[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(10): 10. DOI: 10.1109/JSAC.2013.131011 |
| [4] | HUI Hui, SWINDLEHURST L A, LI Guobing, et al. Secure relay and jammer selection for physical layer security[J]. IEEE Signal Processing Letters, 2015, 22(8): 1147-1151. DOI: 10.1109/LSP.2014.2387860 |
| [5] | MESLEH R Y, HAAS H, SINANOVIC S, et al. Spatial modulation[J]. IEEE Transactions on Vehicular Technology, 2008, 57(4): 2228-2241. DOI: 10.1109/TVT.2007.912136 |
| [6] | FU Jinlin, HOU Chunping, XIANG Wei, et al. Generalised spatial modulation with multiple active transmit antennas[C]// Proceeding of IEEE GLOBECOM Workshops. Piscataway: IEEE Press, 2010: 839-844. DOI: 10.1109/GLOCOMW.2010.5700442. |
| [7] | TAKEUCHI K. Spatial modulation achieves information-theoretically optimal energy efficiency[J]. IEEE Wireless Communications Letters, 2015, 19(7): 1133-1136. DOI: 10.1109/LCOMM.2015.2433271 |
| [8] | XIAO Yue, YANG Zongei, DAN Lilin, et al. Low-complexity signal detection for generalized spatial modulation[J]. IEEE Communications Letters, 2014, 18(3): 403-406. DOI: 10.1109/LCOMM.2013.123113.132586 |
| [9] | CAL-BRAZ J A, SAMPAIO-NETO R. Low-complexity sphere decoding detector for generalized spatial modulation systems[J]. IEEE Communications Letters, 2014, 18(6): 949-952. DOI: 10.1109/LCOMM.2014.2320936 |
| [10] | LIU Wenlong, WANG Nan, JIN Minglu, et al. Denoising detection for the generalized spatial modulation system using sparse property[J]. IEEE Communications Letters, 2014, 18(1): 22-25. DOI: 10.1109/LCOMM.2013.111413.131722 |
| [11] | BASNAYAKAD A, HAAS H. Spatial modulation for massive MIMO [C]// Proceeding of IEEE International Conference on Communications Piscataway: IEEE Press, 2015: 1945-1950. DOI: 10.1109/ICC.2015.7248610. |
| [12] | GUAN Xinrong, CAI Yueming, YANG Weiwei. On the secrecy mutual information of spatial modulation with finite alphabet[C]// Proceeding of International Conference on Wireless Communications and Signal Processing. Piscataway: IEEE Press, 2012: 1-4. DOI: 10.1109/WCSP.2012.6542961. |
| [13] | WU Feilong, YANG Lieliang, WANG Wenjie, et al. Secret precoding-aided spatial modulation[J]. IEEE Wireless Communications Letters, 2015, 19(9): 1544-1547. DOI: 10.1109/LCOMM.2015.2453313 |
| [14] | DONG Lun, HAN Zhu, PETROPULU A P, et al. Improving wireless physical layer security via cooperating relays[J]. IEEE Transactions on Signal Processing, 2010, 58(3): 1875-1888. DOI: 10.1109/TSP.2009.2038412 |
| [15] | JEGANATHAN J, GHRAYEB A, SZCZECINSKI L. Spatial modulation: optimal detection and performance analysis[J]. IEEE Communications Letters, 2008, 12(8): 545-547. DOI: 10.1109/LCOMM.2008.080739 |
 2017, Vol. 49
2017, Vol. 49


