基于军事信息栅格构建的指挥信息系统,不仅是网络化体系作战的基础支撑,也是网络化体系对抗中的重要目标.随着网络化程度的提高,指挥信息系统受到攻击后产生级联失效和系统崩溃的可能性越来越大.对不同攻击条件下指挥信息系统的级联失效特性进行分析,对于提升指挥信息系统的攻防能力十分必要.首先需要对指挥信息系统进行结构建模,复杂网络是建模的重要工具[1].文献[2]提出将复杂网络理论用于分析指挥信息系统结构建模,并建立了FINC模型;文献[3-5]分别针对指挥信息系统的拓扑结构和复杂特性等问题建立了网络模型,并基于各自模型分析了指挥信息系统的异质异构特点、拓扑结构特征和动态交互方式.近年来,复杂网络级联失效成为国内外复杂网络理论研究的热点之一.文献[6]认为耦合网络较单层网络更能反映现实中电力、交通和信息设施等的网络结构特征,并重点研究耦合网络的级联失效问题;文献[7-8]则分别研究了耦合网络在面对级联失效时的脆弱性和鲁棒性,为耦合网络级联失效问题的研究提供了参考.目前,已有学者将相关理论用于研究指挥信息系统级联失效问题.文献[9]将指挥信息系统抽象为复杂网络,对网络节点进行攻击并分析其级联失效特性,较好地度量了指挥信息系统功能网络结构的鲁棒性,但只考虑了系统在功能层面的级联失效问题;文献[10]从节点和业务两个层面构建了双层军事指挥系统网络,克服了单层网络结构建模的不足,但攻击策略设置较单一,无法从不同角度考察系统级联失效特性,不能适应多样化攻击的现实情况.以上成果为指挥信息系统级联失效问题的研究提供了有益借鉴,但对系统结构建模和攻击策略设置等的研究还有待深入.
针对以上问题,本文依据指挥信息系统的结构特征和功能特性构建了双层耦合网络模型,分析了该双层耦合网络的级联失效机理.在此基础上,根据攻击方式和攻击强度的不同,设置了不同的攻击策略,建立了指挥信息系统级联失效特性分析模型.最后以某区域联合防空指挥信息系统为例,构建了双层耦合网络模型,并对模型的基本网络特性和级联失效过程进行了仿真分析,不仅验证了指挥信息系统双层耦合网络模型的有效性,而且分析了该系统在不同攻击策略下的级联失效特性,为进一步提升指挥信息系统的攻防能力提供参考.
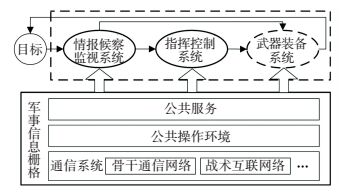
1 指挥信息系统网络结构新一代指挥信息系统是支撑网络化体系作战的复杂军事信息系统,建立在军事信息栅格之上,由情报侦察监视系统、指挥控制系统和武器装备系统构成,是集承载网与各功能网于一体,融合多种通信网系、集成多类业务系统的层级复杂系统[11].传统利用单层复杂网络理论对系统进行结构建模的方法,由于仅考虑底层信息栅格或上层信息系统,因此无法描述两层网络之间的关系,而层级复杂网络建模方法[12-14]能够解决具有耦合关系的多层网络相关问题,更真实地反映层级复杂系统特性,从而为指挥信息系统结构建模提供了新的手段.
|
图 1 指挥信息系统体系构成 Figure 1 CIS architecture |
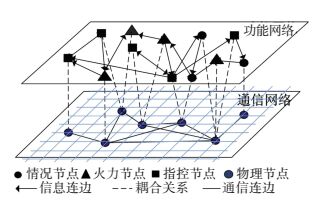
层级复杂网络是指由多个复杂子网构成的层级网络,与单层复杂网络相比,层级复杂网络在描述复杂系统时更全面有效且具实际意义,近年来广泛应用于供应链、交通和通信网络等复杂系统的建模.根据结构特征和功能组成,指挥信息系统可分为通信网络层和功能网络层,如图 2所示.下层是由物理实体节点和通信连接关系构成的通信网络,上层是由功能节点 (如情报、指控和火力) 和信息交互关系构成的功能网络.通信网络根据通信基础网抽象得到,每个节点表示一个物理实体,即物理节点,物理节点之间的连边表示通信连接关系,即两个物理节点间若存在有效通信链路,表示通信连边存在.每个物理节点具有一种或多种功能 (如雷达具有情报功能、预警机具有指控功能和情报功能),可“一对一”或“一对多”耦合映射为功能节点,每个功能节点唯一对应于一个物理节点,表示此功能由该物理节点产生.不同功能节点间可进行信息交互,如情报节点向指控节点传输态势信息、火力节点之间传输协同信息,这种信息交互关系由功能连边表示,功能节点和功能连边构成功能网络.
|
图 2 指挥信息系统网络结构 Figure 2 CIS network structure |
分析可知,指挥信息系统网络结构是一个由通信网络和功能网络耦合而成的双层网络,两层网络之间相互影响、相互作用,并通过节点映射的关系进行耦合.其中,通信网络是功能网络的物理载体,对功能网络形成约束,功能网络是通信网络的保障对象,在一定程度上能够影响通信网络的结构.
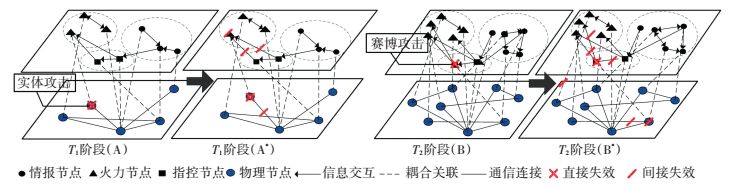
指挥信息系统在增强作战体系信息优势的同时,也增大了由多样化攻击导致的级联失效风险.在体系作战过程中,一方面可通过精确打击和火力压制等“硬打击”(实体打击) 方式破坏指挥信息系统,使部分物理节点失效,导致通信网络层内部级联失效;另一方面,还可通过数据篡改、网络欺骗和拒绝服务等“软攻击”(赛博攻击) 方式破坏系统功能,导致功能节点失效,并引发功能网络层内级联失效.由于指挥信息系统层间耦合关系,物理节点失效将导致与之耦合的功能节点失效,而功能节点失效由于影响信息的生成、传输、处理和共享,同样会给物理节点带来影响.不同攻击方式毁伤指挥信息系统的过程如图 3所示,指挥信息系统在T1阶段遭遇实体打击,网络结构由A变为A*,在T2阶段遭遇赛博攻击,网络结构由B变为B*.
|
图 3 不同攻击方式下指挥信息系统网络毁伤示意 Figure 3 Sketch map of CIS network cascading failure under different attack modes |
综上,指挥信息系统可看作由通信网络和功能网络耦合形成的双层网络,基于双层耦合网络模型分析指挥信息系统级联失效特性,相比传统单层网络模型更接近真实情况.首先构建指挥信息系统双层耦合网络模型,在此基础上,分析指挥信息系统级联失效机理,建立指挥信息系统级联失效特性分析模型.
2 双层耦合网络模型首先进行如下假设:
1) 不考虑指挥信息系统各节点的属性和级别;
2) 物理节点受到战场空间地理位置和约束,两个物理节点之间为通信连接关系,没有方向性;
3) 功能节点间通过信息交互形成信息连边,具有方向性,如由A节点指向B节点的信息连边表示A向B发送某种类型的信息.
2.1 模型构建 2.1.1 通信网络通信网络GP是无向赋权连通网,表示为GP=(VP, EP, WP),VP表示物理节点集合.若GP含有NP个节点,则VP={pi|i=1, 2, …, NP};EP={eij|eij=(pi, pj), pi, pj∈VP}表示任意两个物理节点之间通信链路的集合.设GP中有MP条通信连边,即|EP|= MP;WP=[wpij]NP×NP={w1, w2, w3, …, wMP}为GP边权值的集合,边权wpij用来表示对应通信连边ep的属性特征.若网络结构边权值为1,令aij表示eij=(pi, pj) 的存在性,(pi, pj)∈EP时aij=1,否则为0,则GP的网络结构可用邻接矩阵表示为AP=(aij)NP×NP.
2.1.2 功能网络功能网络GF是有向赋权连通网,表示为GF=(VF, EF, WF),VF为功能节点集合,功能节点由物理节点映射得到.设GF有NF个功能节点,VF={fi|i=1, 2, …, NF}.功能节点通过信息交互实现一定的信息功能,满足指挥信息系统作战任务的信息需求,信息交互连边集合记为EF={e1, 2, e2, 1, e3, 4, …, ei, j}, i, j∈NF, i≠j,|EF|=Mf为信息连边数.由于功能节点之间传输的是不同类型的信息流,因此ei, j为有向边.根据功能节点间的信息交互次数可定义边权值WF,WF={wi, j|i, j∈NF, i≠j}.同样定义AF为GF邻接矩阵,AF=(ai, j)NF×NF,其中ai, j为矩阵元素,且当ai, j=1时,表明存在由fi到fj的信息交互,即 (fi, fj)∈EF, i≠j,否则ai, j=0.
2.1.3 双层耦合网络指挥信息系统双层耦合网络GP-F由通信网络GP和功能网络GF耦合形成,表示为GP-F={GP, GF, RP-F},其中RP-F表示GP的耦合关系,分析知,
| ${r_{ij}}\left\{ {\begin{array}{*{20}{l}} {1,} & {{p_i} \to {f_i}}\\ {0,} & {otherwise.} \end{array}} \right.\quad \quad \left( {{p_i} \in {V_P},{f_j} \in {V_P}} \right)$ |
将GP和GF之间的耦合关系看作耦合边,双层耦合网络还可表示为GP-F=(V, E, W).其中:V表示表示网络GP-F节点的集合,V=VP∪VF;E表示网络GP-F连边的集合,E=EP∪EF∪ER,ER表示GP和GF之间存在耦合边的集合;W表示网络GP-F边权值的集合,且W=WP∪WF∪WR,其中WR表示耦合边权值集合,为不失一般性,令W中的权值均为1.
2.1.4 耦合强度耦合强度是指不同网络间耦合边数占规模较小网络节点数的比值.在指挥信息系统双层耦合网络结构中,每个物理节点均可耦合映射为一或多个功能节点,根据耦合强度的概念可知,指挥信息系统耦合强度δ为功能节点数与物理节点数的比值,即
| $\delta = \frac{{{N_F}}}{{{N_P}}}$ |
由于δ是反映指挥信息系统“物理—功能”耦合特征的一个结构参数,因此,δ值越大,表示每个物理节点平均承载的功能越多,即指挥信息系统的服务承载能力越强. δ值应根据实际指挥信息系统中物理节点所承载的信息功能数确定.在仿真分析时,考虑到指挥信息系统去中心化、负载均衡和分布式服务的特征,可通过计算实际指挥信息系统的δ值,将功能平均耦合于物理节点.
综上,构建指挥信息系统双层耦合网络模型GM,并表示为多元组GM=Θ(GP, GF, GP-F).
2.2 节点重要度网络统计特性是揭示网络拓扑结构特征的重要参考,包括节点度、度分布、特征路径长度和聚类系数等[2],根据级联失效问题研究需要,本文重点分析与节点重要性相关的网络统计特性,包括节点度和节点介数,并在此基础上定义节点重要度.
2.2.1 节点度与度分布节点度d(vi) 是指与节点vi相连的边的数目,在一定程度上反映了节点的重要程度,是网络局部结构特性的表征.对于无向网络,节点度表示与该节点直接相连的节点数,即邻居节点个数;对于有向网络,节点度可根据边的指向进一步分为节点入度和节点出度;对于赋权网络,则在节点度的基础上进一步定义节点强度w(vi),即节点vi相邻边的权重之和.双层耦合网络中的节点度可分为节点内部度和节点外部度.其中,节点内部度d(vi) 是指节点vi在该节点所处网络层内部所拥有的边的数目,平均内部度用dm表示;节点外部度d'(vi) 是指节点vi所拥有的耦合边的数目,平均外部度用dm′表示.分析知,功能网络的平均外部度为1,通信网络的平均外部度为δ.
度分布p(k) 是指随机选择节点vi的度d(vi) 等于k的概率,根据度分布可初步判断网络的连通性和均匀性.
2.2.2 节点介数节点vi的介数,是指经过节点vi的最短路径数占所有最短路径数的比例,反映了节点vi对信息传递的控制和影响能力,可表示为
| $b\left( {{v_i}} \right) = \frac{2}{{n\left( {n - 1} \right)}}\sum\limits_j^N {\sum\limits_k^N {\frac{{{g_{jk}}\left( i \right)}}{{{g_{jk}}}}} } .$ |
其中i≠j≠k, k>j,gkj(i) 表示vj和vk间经过vi的最短路径数,gjk表示vj和vk间所有最短路径数.节点介数度量了节点位于其他节点对中间的程度,反映了节点控制信息传递和流通的能力.分析知b(vi)∈[0, 1],b(vi)=0表示vi处于网络边缘,b(vi)=1表示vi处于网络核心,其值越大表明该节点在网络中起到越重要的中介和核心作用.
2.2.3 节点重要度节点度和节点介数分别从节点对局部网络结构和信息传递控制两个方面体现了节点的重要程度,在节点度和节点介数的基础上,提出节点重要度的概念.节点重要度是指节点对于节点所处网络的影响程度,已知节点vi的度为d(vi),节点介数为b(vi),则节点vi的重要度为
| $s\left( {{v_i}} \right) = \alpha d\left( {{v_i}} \right) + \beta b\left( {{v_i}} \right).$ |
其中
级联失效是指网络内某节点的失效将引发更多节点失效的情况,指挥信息系统双层耦合网络级联失效存在层内失效和层间失效两种级联失效类型.
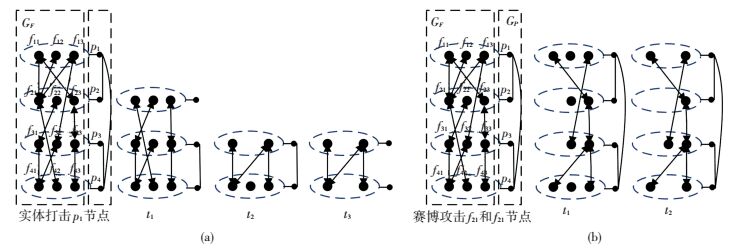
3.1.1 层内失效层内失效是指由于单层网络节点失效引起的在该层网络内部的节点级联失效的过程.具体过程为:当某节点失效时,与该节点相连的连边 (通信链路或信息交互关系) 失效,因此,若该节点的邻居节点度值为1,则该节点失效将导致其邻居节点失效.例如在图 4(a)中,实体攻击GP中的p1节点导致其失效,由于该节点是p2节点的唯一相邻节点,因此p2节点失效.现有指挥信息系统级联失效问题大多仅考虑了层内失效的情况.
|
图 4 双层耦合网络级联失效过程 Figure 4 Cascading failure of bi-layer coupled network |
层间失效是指在双层耦合网络中,由某层节点失效引起的与之耦合的另一网络层节点失效的过程.由于功能网络层GF的节点是由通信网络层GP的物理节点映射得到,GP-F两层网络之间存在耦合关系,因此,若GP中某物理节点失效,将导致GF中与之耦合的功能节点失效;反之,若与某物理节点耦合的所有功能节点均失效,则该物理节点将不再与其他物理节点进行通信,可认为该物理节点功能丧失,成为无效节点.
3.1.3 失效规模极大互联簇是衡量网络受攻击后维持性能的重要指标[15],假设GP中某物理节点受到攻击失效,则对应GF中的功能节点失效,与之相连的信息连边消失,经多次迭代后,网络GP-F处于稳定状态,此时处于极大互联簇的节点才能够保持相应功能.在极大互联簇的基础上,定义基于节点度的失效规模测度,设GP-F为初始网络结构,GP-F′为节点vi失效后的网络结构,则由节点失效vi引起的网络失效规模S(vi) 为
| $s\left( {{v_i}} \right) = \frac{{\sum\limits_{{v_k} \in V'} {d\left( {{v_k}} \right)} }}{{\sum\limits_{{v_k} \in V} {d\left( {{v_k}} \right) - d\left( {{v_i}} \right)} }}.$ |
假设1 攻击策略为蓄意攻击[16],即敌方优先攻击重要度较大的节点,攻击方式包括实体打击、赛博攻击和混合攻击三种.
假设2 网络节点受到攻击失效时,只有属于网络极大互联簇的节点能够保持功能,计算极大互联簇节点度变化情况即可判断网络受损情况.
3.2.1 攻击方式1) 实体打击.实体打击包括对指挥信息系统物理实体的精确打击和摧毁等,主要以节点毁伤的方式破坏通信网络的网络结构.实体打击导致的级联失效过程如图 4(a)所示:t1阶段,通信网络GP中重要度较大的节点p1遭受敌方实体打击而失效,耦合节点f11, f12, f13失效,且与此3个节点相连的边e12, e14消失;t2阶段,不属于GP极大互联簇的物理节点p2失效,导致与p2耦合的功能节点f21, f22, f23失效,与之相连的信息连边被删除;不属于GF极大互联簇的功能节点f32失效,被删除;t3阶段,由于f21与f42之间的信息连边消失,导致不属于GF极大簇的节点f42失效被删除;网络结构达到稳态.
2) 赛博攻击.赛博攻击能够通过数据篡改、网络欺骗和拒绝服务等方式,造成指挥信息系统功能失效、信息交互阻断,并间接影响通信网络中的物理节点 (如果物理节点所有信息功能失效,则认为该物理节点失效).赛博攻击导致的级联失效过程如图 4(b)所示:t1阶段,功能网络GF中重要度较大的节点f21, f31受到赛博攻击失效,节点和对应信息连边消失;t2阶段,不属于GF极大互联簇的节点f12, f22, f42失效,被删除;网络结构达到稳态.
3) 混合攻击.混合攻击是指在给定攻击强度条件下,按照一定比例向实体打击和赛博攻击分配攻击强度,并根据所分配的攻击强度对指挥信息系统进行混合攻击,从而破坏系统的网络结构、降低系统的网络性能.
假设某指挥信息系统初始状态的网络结构为GP-F,某时刻系统遭遇敌方攻击 (实体打击、赛博攻击或混合攻击),致使部分节点失效,随着网络失效特性不断传播,网络结构不断变化,直至节点数不再发生改变为止,设此时网络结构为G′P-F.网络结构GP-F→G′P-F,计算网络失效规模,并分析指挥信息系统级联失效特性.
3.2.2 攻击强度体系对抗过程中,破坏指挥信息系统关键节点是敌方的首要目标,因此,敌方在对指挥信息系统进行攻击时,会首选节点重要度较大的节点,称这些节点为重要节点.据此定义攻击强度,即受到攻击的重要节点的数目占总的网络节点数的比例,设为ρ,0<ρ<1.改变ρ值并计算网络平均失效规模S,可分析不同攻击强度下,指挥信息系统的级联失效特性.在设置ρ时,应首先按照节点重要度对网络节点进行降序排列,然后选择其中排序靠前的节点进行攻击,以实体打击为例,步骤如下:
1) 将通信网络GP中NP个物理节点按照节点重要度进行降序排列,序号为1, 2, …, NP;
2) 设对GP-F实施攻击强度为ρ的实体打击,攻击序号为1, 2, …, [NPρ]的节点,上述节点的失效将引发GP和GF两层网络的级联失效;
3) 自步骤1) 开始循环执行,至网络节点数不再发生变化后,分别统计GP、GF和GP-F的平均失效规模.
混合攻击包括实体打击和赛博攻击,用比例系数α来表示实体攻击占混合攻击的比重,0<α<1.当混合攻击的攻击强度为ρ时,实体打击的攻击强度为αρ,赛博攻击的攻击强度为 (1-α)ρ.混合攻击时,攻击强度、实体打击与赛博攻击的比例和顺序均可能导致不同的级联失效.
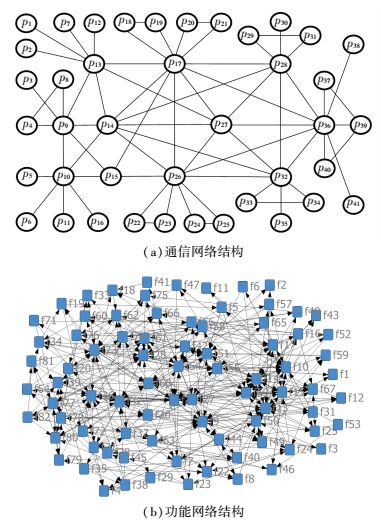
4 仿真分析以某作战想定中的区域联合防空指挥信息系统为例,进行仿真分析.根据想定,该指挥信息系统可抽象为双层耦合网络,且耦合强度为2.其中,通信网络包括41个物理节点和67条通信链路,网络结构如图 5(a)所示.根据指挥信息系统负载均衡、去中心化和分布式服务思想,平均分配82个功能节点,一个物理节点可耦合映射为两个功能节点,且pi→fi, i+41, i∈(1, 2, …, 41).对功能节点间的信息交互关系进行统计,得到如图 5(b)所示的功能网络结构,计算知该指挥信息系统共有434条有向信息连边.
|
图 5 指挥信息系统双层耦合网络结构 Figure 5 CIS bi-layer coupled network structure |
在指挥信息系统中,存在少量节点如情报和指控中心,既是通信网络中的重要节点,又因承担较重的信息收集、处理和分发任务,也是功能网络中的重要节点.此外还存在部分节点,由于在执行作战任务时能够与其他多个节点进行信息交互,因此在功能网络中的重要程度较高,但由于受到地理位置、层次级别和通信手段等的约束,这些节点与其他节点通信连接少,并不属于通信网络中的重要节点.
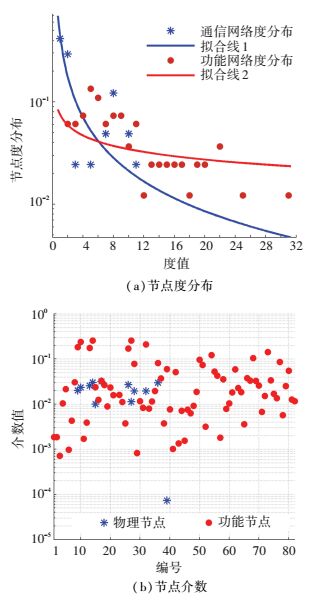
4.1 GM模型已知NP=41, NF=82, MP=67, MF=434,邻接矩阵AP和AF,耦合矩阵R=[I41I41],分别计算度分布和节点介数,结果如图 6所示. 图 6(a)为GP和GF的节点度分布图,可以看出,两层网络都表现出无标度特征,表示网络由少数度值较大的节点和大量度值较小的节点构成,因此,若对网络实施蓄意攻击,特别是对拥有较大度值的节点进行攻击,网络将迅速失效[17-18]. 图 6(b)为节点介数图,其中大部分物理节点的介数值为0,表示GP中处于边缘的节点较多,而功能节点介数值为0的节点较少,且介数值的分布更加均匀,表示GF扁平化特征更明显[10].计算可知,GP具有较高的平均介数值,为0.217,而GF的平均介数值为0.112,因此,相比于GF,GP表现出更明显的向某个点集中的趋势,这主要是由于通信网络受到通信方式、地理位置和气象环境等现实条件的限制,大量物理节点不能同任意多个其他物理节点进行通信连接,因此存在大量处于网络边缘的物理节点,而功能网络不受此条件限制.以上分析与实际指挥信息系统的结构特性一致,说明GM能够较好地描述指挥信息系统结构.在此基础上,对指挥信息系统级联失效特性进行仿真分析.
|
图 6 度分布与节点介数 Figure 6 Degree distributing and node betweenness |
攻击方式包括实体打击、赛博攻击和混合攻击三种;攻击强度0<ρ<1,具体设置方法见3.2.2节,仿真分析时令ρ∈(0.01, 0.99),递进步长为0.025.
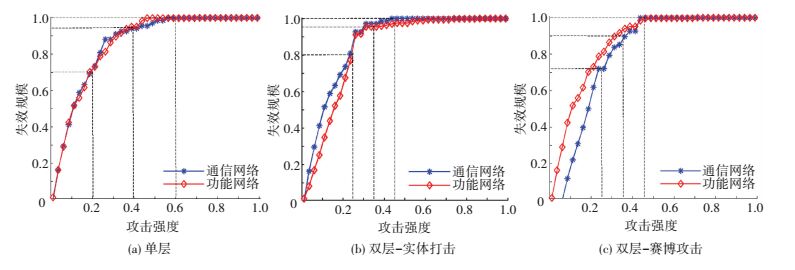
4.2.1 级联失效特性对比分析 4.2.1.1 单层网络级联失效考察单层网络的级联失效特性,包括实体打击所导致的通信网络GP层内级联失效,以及赛博攻击所导致的功能网络GF层内级联失效,结果如图 7(a)所示.可知:攻击强度不同,系统失效规模不同;实体打击和赛博攻击导致的层内级联失效趋势一致;蓄意攻击破坏性强,当ρ=0.2时,GP和GF的失效规模均高达70%,当ρ=0.6时,GP和GF已完全崩溃,系统瘫痪;当ρ∈(0.2, 0.35) 时,GP失效规模较大,当ρ∈(0.35, 0.55) 时,GF失效规模较大.
|
图 7 不同攻击强度下网络级联失效 Figure 7 Cascading failure of network under different attack intensities |
分析可知,在敌方蓄意攻击下,网络级联失效规模将随着ρ的增加而迅速扩大,当ρ=0.6时,系统已完全瘫痪,以上结论与传统基于单层网络建模方法对指挥信息系统级联失效分析所得的结论基本一致[16].
4.2.1.2 双层网络级联失效考察基于双层耦合网络模型的指挥信息系统级联失效特性.实施攻击强度为ρ的实体打击,级联失效结果如图 7(b)所示.在遭受实体打击后,GP的失效将迅速引发GF的级联失效,且当ρ∈(0.25, 0.35) 时,两层网络失效规模保持一致,但当ρ∈(0, 0.25)∪(0.35, 1) 时,GP失效规模大于GF.分析可知,这是由于在GF中存在部分节点重要度与相耦合物理节点的节点重要度不一致的功能节点,该结论符合4.1节的分析,说明了模型的一致合理性.
实施攻击强度为ρ的赛博攻击,级联失效结果如图 7(c)所示.在系统完全失效前,赛博攻击导致的GF失效规模总是大于GP的失效规模,这是由于若要物理节点失效,则必须满足与之耦合的所有功能节点均失效.当ρ=0.25时,实体打击造成的失效规模为0.8,高于赛博攻击 (0.72),即实体打击对系统的破坏更严重;当ρ>0.45时,无论赛博攻击还是实体打击,均导致系统完全失效.
4.2.1.3 对比分析图 7(a)表示了基于传统单层复杂网络理论所建立的网络模型,在受到实体打击或赛博攻击后的级联失效特性;图 7(b)和(c)则分别表示了在实体打击和赛博攻击方式下,双层耦合网络模型的级联失效特性.对比图 7(a)、(b)和 (c) 可以看出:当ρ∈(0, 0.25) 时,单层网络级联失效特性与双层网络级联失效特性相似,采用双层耦合网络分析指挥信息系统级联失效问题的优势不明显;但当ρ>0.25时,双层耦合网络的级联失效规模迅速增加,在ρ=0.45时即造成系统完全失效,而单层网络级联失效的曲线相对平缓,这是由于双层耦合网络考虑了指挥信息系统的“物理—功能”耦合关系,级联失效传播效应更明显,也更加贴近真实指挥信息系统级联失效情况.此外,对比图 7(b)和(c)可知,攻击强度较小时,赛博攻击能够达到与实体打击相近的攻击效果,但当攻击强度较大时,赛博攻击的效果不如实体打击.考虑到赛博攻击成本较小,因此在进行局部体系对抗时,可优先选用赛博攻击的方式对敌方指挥信息系统关键节点进行破坏.
4.2.2 混合攻击条件下的级联失效混合攻击的攻击比例和攻击顺序不同,指挥信息系统级联失效特性也不同,以下分别进行分析.
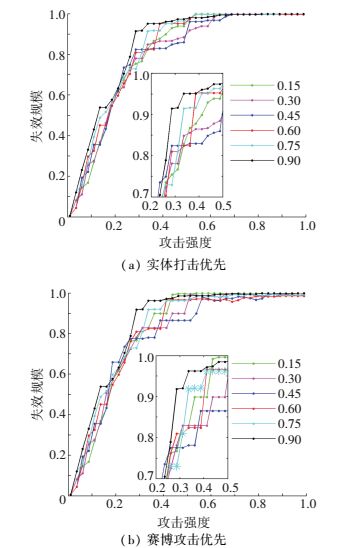
4.2.2.1 攻击比例设混合攻击攻击比例为α,据3.2.2节的定义知α∈(0, 1).设置不同的α值,可考察对指挥信息系统进行混合攻击时,实体打击和赛博攻击所占比例对系统失效规模的影响.令步长为0.15,则α=(0.15, 0.30, 0.45, 0.60, 0.75, 0.90),且α越大,表示实体打击在混合打击中所占比例越高. 图 8显示了不同攻击强度和不同攻击比例条件下系统的级联失效特性,考虑到攻击顺序的影响,图 8(a)和图 8(b)分别显示了实体打击优先和赛博攻击优先的情况.
|
图 8 不同攻击比例的混合攻击 Figure 8 Mixed attack mode based on different attack proportion |
由图 8可以看出,相同强度的混合攻击,由于实体打击和赛博攻击所占比例的不同,将导致不同的双层耦合网络级联失效规模.当ρ<0.25时,α越大 (实体打击比例高),指挥信息系统的级联失效规模越大,且α=0.9时系统失效规模最大;自ρ>0.25开始,不同α导致的系统失效规模差距表现出不确定性,这是由于此时系统的失效规模已接近80%,网络规模较小的情况下,结论不具普遍性.
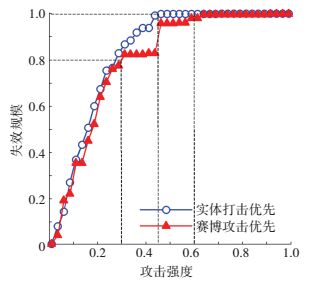
4.2.2.2 攻击顺序如图 9所示,混合攻击包括赛博攻击优先和实体打击优先两种方式.设置攻击比例α=0.3,分别考察实体打击优先和赛博攻击优先条件下系统的级联失效特性.当ρ∈(0, 0.3) 时,由攻击顺序导致的失效规模差异很小;当ρ∈(0.3, 0.6) 时,采取实体打击优先的攻击顺序,将导致指挥信息系统产生较大规模的级联失效;ρ>0.45时,实体打击优先的混合攻击将导致系统完全失效,ρ>0.6时,赛博攻击优先的混合攻击导致指挥信息系统完全失效.分析可知,在给定攻击强度和攻击比例下,攻击顺序对系统级联失效规模的影响不能忽视,尤其是攻击强度较大的情况下,更应重视实体打击与赛博攻击的攻击顺序.
|
图 9 不同攻击顺序的混合攻击 Figure 9 Mixed attack mode based on different attack order |
综上,在体系对抗过程中,考虑到实体打击的成本一般高于赛博攻击,且攻击强度较小时,两种攻击方式对系统网络结构的影响差别不大,因此,若发生小规模局部对抗,应首先考虑破坏对方指挥信息系统的功能网络,同时重点关注自身网络安全、防范赛博攻击;在大规模、大范围对抗的情况下,由于实体打击产生的效果十分明显,因此,需要加强对关键物理实体进行防护和备份,在对己方指挥信息系统进行安全防护的前提下,综合考虑攻击成本和效果,选择合理的攻击方式破坏对方指挥信息系统,以最大程度削弱其体系优势.
5 结语本文针对指挥信息系统级联失效研究中结构建模简单和攻击方式单一问题,提出指挥信息系统双层耦合网络结构模型,并基于该模型设置了不同的攻击方式、攻击强度和攻击比例等,实现对指挥信息系统级联失效特性的全面分析.仿真分析结果表明,构建的双层耦合网络模型不仅能够准确反映指挥信息系统的结构特征,而且利用该模型还能够对系统在多种攻击方式和不同攻击强度下的级联失效特性进行分析.下一步将重点围绕不同耦合强度的指挥信息系统在级联失效特性方面存在的差异,以及基于耦合关系对指挥信息系统网络结构进行优化等问题展开研究,为增强指挥信息系统的抗毁性和鲁棒性提供借鉴.
| [1] |
胡晓峰, 杨靖宇, 司光亚, 等.
战争工程论——走向信息时代的战争方法学[M]. 北京: 国防大学出版社, 2012: 251-260.
HU Xiaofeng, YANG Jingyu, SI Guangya, et al. War complex system simulation analysis & experimentation[M]. Beijing: National Defense University Press, 2012: 251-260. |
| [2] | DEKKER A. Applying social network analysis concepts to military C4ISR architectures[J]. Connections, 2002, 24(3): 93-103. |
| [3] |
蓝羽石, 张杰勇. 基于超网络理论的网络中心化C4ISR系统结构模型和分析方法[J].
系统工程理论与实践, 2016, 36(5): 1239-1251.
LAN Yushi, ZHANG Jieyong. The model and the analysis method of network-centric C4ISR structure based on super network theory[J]. System Engineering-Theory & Practice, 2016, 36(5): 1239-1251. DOI: 10.12011/10000-6788(2016)05-1239-13 |
| [4] |
王再奎, 马亚平, 桑景瑞, 等. 基于复杂网络理论的指挥信息网络拓扑模型研究[J].
指挥控制与仿真, 2011, 33(2): 8-11.
WANG Zaikui, MA Yaping, SANG Jingrui, et al. Research on network topology model of command information system based on complex networks[J]. Command Control & Simulation, 2011, 33(2): 8-11. DOI: 10.3969/j.issn.1673-3819.2011.02.003 |
| [5] |
张萌萌, 陈洪辉, 罗爱民, 等. 基于动态调整的C4ISR系统结构灵活性分析[J].
系统工程与电子技术, 2016, 38(3): 563-568.
ZHANG Mengmeng, CHEN Honghui, LUO Aimin, et al. C4ISR system structure flexibility analysis based on dynamic adjustment[J]. System Engineering and Electronics, 2016, 38(3): 563-568. DOI: 10.3969/j.issn.1001-506X.2016.03.14 |
| [6] | SHEKHTMAN L M, DANZIGER M M, HAVLIN S. Recent advances on failure and recovery in networks of networks[J]. Chaos, Solitons & Fractals, 2016, 90(9): 28-36. DOI: 10.1016/j.chaos.2016.02.002 |
| [7] | SUN S, WU Y, MA Y, et al. Impact of degree heterogeneity on attack vulnerability of interdependent networks[J]. Nature, 2016, 6: 32983. DOI: 10.1038/srep32983 |
| [8] |
陈世明, 吕辉, 徐青刚, 等. 基于度的正/负相关相依网络模型及其鲁棒性研究[J].
物理学报, 2015, 64(4): 1-11.
CHEN Shiming, LV Hui, XU Qinggang, et al. The model of interdependent network based on positive/negative correlation of the degree and its robustness study[J]. Acta Phys Sin, 2015, 64(4): 1-11. DOI: 10.7498/aps.64.048902 |
| [9] |
张杰勇, 易侃, 王珩, 等. 考虑级联失效的C4ISR系统结构动态鲁棒性度量方法[J].
系统工程与电子技术, 2016, 38(9): 2072-2079.
ZHANG Jieyong, YI Kan, WANG Heng, et al. Dynamic robustness measure method considering cascading failure for C4ISR system structure[J]. System Engineering and Electronics, 2016, 38(9): 2072-2079. DOI: 10.3969/j.issn.1001-506X.2016.09.15 |
| [10] |
沈迪, 李建华, 熊金石, 等. 一种基于介数的双层复杂网络级联失效模型[J].
复杂系统与复杂性科学, 2014, 11(3): 12-18.
SHEN Di, LI Jianhua, XIONG Jinshi, et al. A cascading failure model of double layer complex networks based on betweenness[J]. Complex System and Complexity Science, 2014, 11(3): 12-18. DOI: 10.13306/j.1672-3813.2014.03.003 |
| [11] |
蓝羽石, 毛少杰, 王珩.
指挥信息系统结构理论与优化方法[M]. 北京: 国防工业出版社, 2015: 12-16.
LAN Yushi, MAO Shaojie, WANG Heng. Theory and optimization of C4ISR system structure[M]. Beijing: National Defense Industry Press, 2015: 12-16. |
| [12] | BOCCALETTI S, BIANCONI G, CRIADO R, et al. The structure and dynamics of multilayer networks[J]. Physics Reports, 2014, 544(1): 1-122. DOI: 10.1016/j.physrep.2014.07.001 |
| [13] | DEDOMENICO M, GRANELL C, PORTER M A, et al. The physics of spreading processes in multilayer networks[J]. Nature Physics, 2016, 22(8): 901-906. DOI: 10.1038/npphys386 |
| [14] | MIEGHEM P V. Interconnectivity structure of a general interdependent network[J]. Physics Review E, 2016, 93(4): 042305. DOI: 10.1103/PhysRevE.93.042305 |
| [15] | VEREMYEV A, SOROKIN A, BOGINSKI V, et al. Minimum vertex cover problem for coupled interdependent networks with cascading failures[J]. European Journal of Operational Research, 2014, 232: 499-511. DOI: 10.1016/j.ejor.2013.08.008 |
| [16] |
易侃, 王珩, 毛少杰, 等. 基于信息流的网络化C4ISR系统结构抗毁性分析方法[J].
系统工程与电子技术, 2014, 36(8): 1544-1550.
YI Kan, WANG Heng, MAO Shaojie, et al. Information flow based survivability assessment method for networked C4ISR system structure[J]. Systems Engineering and Electronics, 2014, 36(8): 1544-1550. DOI: 10.3969/j.issn.1001-506X.2014.08.16 |
| [17] |
路向阳, 贾丽娟, 王硕, 等. 具有相依特性的航天测控网稳定性分析[J].
飞行器测控学报, 2015, 32(2): 147-152.
LU Xiangyang, JIA Lijuan, WANG Shuo, et al. Analysis of the robustness of TT & C networks with interdependent characteristics[J]. Journal of Spacecraft TT & C Technology, 2015, 32(2): 147-152. DOI: 10.7642/j.issn.1674-5620.2015-02-0147-06 |
| [18] |
刘润然, 贾春晓, 章剑林, 等. 相依网络在不同攻击策略下的鲁棒性[J].
上海理工大学学报, 2012, 34(3): 235-239.
LIU Runran, JIA Chunxiao, ZHANG Jianlin, et al. Robustness of interdependent networks under several intentional attack strategies[J]. Jorunal of University of Shanghai for Science and Technology, 2012, 34(3): 235-239. |
 2017, Vol. 49
2017, Vol. 49


