多输入多输出 (Multiple-input-multiple-output, MIMO) 雷达作为一种新兴的雷达体制,成为目前国内外研究热点. MIMO雷达通过每个阵元发射不同波形获得特有的性能优势,因此根据实际应用需求设计MIMO雷达发射波形具有重要意义. MIMO雷达发射方向图由发射信号的协方差矩阵决定.为提高发射功率利用率,文献[1-6]结合实际的雷达工作模式分别对发射信号协方差矩阵进行优化,形成具有一定形状的发射方向图,从而增强目标反射信号并降低杂波,但是在实际应用中需要根据优化的协方差矩阵得到具体的发射波形.为避免上述问题,文献[7-8]提出无需合成协方差矩阵的方向图设计方法, 文献[9]则利用发射信号加权矩阵,将波形优化问题转化为发射信号加权矩阵的优化问题.文献[10]对基于发射加权矩阵所得到的优化波形模糊方程进行了研究,分析该方法所得优化波形模糊抑制能力. MIMO雷达信号输出质量不仅与发射波形有关,而且接收端滤波器也直接决定了雷达信号的输出质量.为进一步提高雷达工作性能,文献[11-12]分别提出了雷达发射波形和接收滤波器联合优化设计方法,但是上述联合优化设计方法没有考虑到发射波形的峰均比 (peak-to-average-ratio, PAR) 等实际约束条件.为解决该问题,文献[13-16]分别针对杂波条件下不同目标信号模型,以最大SINR为准则,结合实际发射波形需要满足恒包络或PAR等约束条件,设计了不同的雷达发射波形和接收滤波器联合优化算法,但是该类算法需要通过凸优化得到发射波形协方差矩阵,再根据协方差矩阵合成具体发射波形,当信号编码较长时计算量巨大,不能满足雷达应用实时性要求.为降低波形优化计算复杂度,文献[17]对基于发射加权矩阵的MIMO雷达发射波形和接收滤波器进行了联合优化设计,但是该方法并没有考虑实际应用条件下算法的稳健性,而且算法采用类凸优化方法计算加权向量的协方差矩阵,在中间迭代过程中需要根据每次优化后的协方差矩阵合成具体加权向量用于优化接收滤波器,计算量仍然较大.
针对上述问题,结合实际应用中强杂波条件下弱目标信号所存在的方向失配以及阵元发射功率约束等情况,本文提出一种基于发射加权矩阵的稳健MIMO雷达发射波形和接收滤波器联合优化设计方法.首先针对目标信号来波方向的不确定集,以最差情况下雷达输出信号SINR最优为目标,以相同的阵元发射功率为约束条件构造发射波形和接收滤波器联合优化模型;然后利用序列优化、Charnes-Cooper转换和半正定松弛,将非凸的联合优化问题转化为关于发射加权矩阵和接收滤波器的子凸优化问题进行迭代求解;最后通过随机向量合成方法得到具体的发射加权矩阵和接收滤波器向量.所提方法在提高算法稳健性的同时,通过对发射加权矩阵进行优化,大大降低了算法计算复杂度,且优化模型满足实际工程中对阵元发射功率的约束.
1 信号模型设一集中式MIMO雷达发射阵元个数为均匀线阵,接收阵元个数为Mr.一组基带信号向量为s(n)=[s1(n, s2(n), …, sk(n)]T, 不同基带信号之间两两相互正交,n=1, 2, …, N,其中N为基带信号的编码长度.在发射加权矩阵作用下,雷达发射信号向量为
| $ \mathit{\boldsymbol{x}}\left( n \right) = {\left[ {{x_1}\left( n \right),{x_2}\left( n \right), \cdots ,{x_{{M_t}}}\left( n \right)} \right]^{\rm{T}}} = Cs\left( n \right), $ |
其中C为发射加权矩阵且C∈CMt×K,K为正交基带信号个数.假设远场X方向存在一点目标,在不同方向θj,j=1, …, Q,存在Q个相互独立的杂波反射点.在时刻n目标位置处接收到的雷达信号为
| $ {y_t}\left( n \right) = {\alpha _0}\mathit{\boldsymbol{a}}_t^{\rm{T}}\left( {{\theta _0}} \right)\mathit{\boldsymbol{Cs}}\left( n \right). $ |
其中,α0为目标反射系数,αt(θ0)=
| $ {\mathit{\boldsymbol{y}}_t}\left( n \right) = {\alpha _0}{\mathit{\boldsymbol{a}}_r}\left( {{\theta _0}} \right)\mathit{\boldsymbol{a}}_t^{\rm{T}}\mathit{\boldsymbol{Cs}}\left( n \right). $ |
其中,αr(θ0)=
| $ {\mathit{\boldsymbol{y}}_c}\left( n \right) = \sum\limits_{i = 1}^Q {{\alpha _i}{\mathit{\boldsymbol{a}}_r}\left( {{\theta _i}} \right)\mathit{\boldsymbol{a}}_t^{\rm{T}}\left( {{\theta _i}} \right)\mathit{\boldsymbol{Cs}}\left( n \right)} . $ |
其中,αi为不同杂波点反射系数.接收端接收到总的信号为
| $ \begin{array}{l} \mathit{\boldsymbol{y}}\left( n \right) = {\mathit{\boldsymbol{y}}_t}\left( n \right) + {\mathit{\boldsymbol{y}}_c}\left( n \right) + \mathit{\boldsymbol{v}}\left( n \right) = \\ \;\;\;\;\;\;\;\;\;\;{\alpha _0}{\mathit{\boldsymbol{a}}_r}\left( {{\theta _0}} \right)\mathit{\boldsymbol{a}}_t^{\rm{T}}\left( {{\theta _0}} \right)\mathit{\boldsymbol{Cs}}\left( n \right) + \\ \;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^Q {{\alpha _i}{\mathit{\boldsymbol{a}}_r}\left( {{\theta _i}} \right)\mathit{\boldsymbol{a}}_t^{\rm{T}}\left( {{\theta _i}} \right)\mathit{\boldsymbol{Cs}}\left( n \right)} + \mathit{\boldsymbol{v}}\left( n \right). \end{array} $ |
其中,υ(n) 为n时刻系统接收到的高斯白噪声且均值为0, 方差为σ2IMr×Mr.在一个处理间隔内接收端接收到的信号矩阵为
| $ \mathit{\boldsymbol{Y = }}{\alpha _0}{\mathit{\boldsymbol{a}}_r}\left( {{\theta _0}} \right)\mathit{\boldsymbol{a}}_t^{\rm{T}}\left( {{\theta _0}} \right)\mathit{\boldsymbol{Cs}} + \sum\limits_{i = 1}^Q {{\alpha _i}{\mathit{\boldsymbol{a}}_r}\left( {{\theta _i}} \right)\mathit{\boldsymbol{a}}_t^{\rm{T}}\left( {{\theta _i}} \right)\mathit{\boldsymbol{Cs}}} + \mathit{\boldsymbol{V}}. $ |
其中,S=[s(1), s(2), …, s(N)]∈CK×N为基带信号矩阵,V∈CMr×N为噪声矩阵.接收端接收信号经过匹配滤波后,输出向量化信号为
| $ \begin{array}{l} \mathit{\boldsymbol{y}} = {\mathit{\boldsymbol{y}}_t} + {\mathit{\boldsymbol{y}}_c} + \mathit{\boldsymbol{v = }}{\alpha _0}{\mathit{\boldsymbol{a}}_r}\left( {{\theta _0}} \right) \otimes {\mathit{\boldsymbol{C}}^{\rm{H}}}{\mathit{\boldsymbol{a}}_t}\left( {{\theta _0}} \right) + \\ \;\;\;\;\;\;\sum\limits_{i = 1}^Q {{\alpha _i}{\mathit{\boldsymbol{a}}_r}\left( {{\theta _i}} \right) \otimes {\mathit{\boldsymbol{C}}^{\rm{H}}}{\mathit{\boldsymbol{a}}_t}\left( {{\theta _i}} \right) + \mathit{\boldsymbol{v}}} . \end{array} $ |
其中,υ∈CMr×K为匹配滤波器输出噪声向量,均值为0, 方差为σ2IMr
由于SINR能够直接决定雷达在目标识别和参数估计等应用中的性能[13-16],因此本节以MIMO雷达输出信号SINR为指标,结合实际应用中雷达发射阵元功率一致的约束条件,对杂波条件下雷达发射波形和接收滤波器进行联合优化.设接收端滤波器为w∈CMrK×1,则信号向量y经过w滤波后输出信号SINR为
| $ \begin{array}{l} {\rm{SINR}}\left( {\mathit{\boldsymbol{w}},\mathit{\boldsymbol{C}}} \right) = \frac{{{{\left| {{\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{y}}_t}} \right|}^2}}}{{E\left[ {{{\left| {{\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{y}}_c}} \right|}^2}} \right] + E\left[ {{{\left| {{\mathit{\boldsymbol{w}}^{\rm{H}}}\mathit{\boldsymbol{v}}} \right|}^2}} \right]}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{{\left| {{\alpha _0}} \right|}^2}{{\left| {{\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{a}}_r}\left( {{\theta _0}} \right) \otimes {\mathit{\boldsymbol{C}}^{\rm{H}}}{\mathit{\boldsymbol{a}}_t}\left( {{\theta _0}} \right)} \right|}^2}}}{{{\mathit{\boldsymbol{w}}^{\rm{H}}}\Sigma \left( \mathit{\boldsymbol{C}} \right)\mathit{\boldsymbol{w + }}{\mathit{\boldsymbol{w}}^{\rm{H}}}\mathit{\boldsymbol{Mw}}}}, \end{array} $ | (1) |
其中,M=E(vvH)=σ2IMrK,Σ(C)=
在较强的杂波环境中,杂波反射点的方向和强度等统计信息可以通过认知等方法获得.相对于较强的杂波信号,目标反射信号较弱导致目标信号的来波方向存在失配误差,因此为保证雷达系统性能,需要对所有可能的目标信号来波方向进行优化设计.同时考虑到在工程应用中发射功率的约束条件,需要MIMO雷达发射加权矩阵满足如下条件:
| $ {\rm{tr}}\left( {{\bf{C}}{{\bf{C}}^{\rm{H}}}} \right) = E, $ | (2) |
| $ \mathit{\boldsymbol{e}}_i^{\rm{T}}\mathit{\boldsymbol{C}}{\left( {\mathit{\boldsymbol{e}}_i^{\rm{T}}\mathit{\boldsymbol{C}}} \right)^{\rm{H}}} = \frac{E}{{{M_t}}},i = 1,2, \cdots ,{M_t}. $ | (3) |
其中,E为总的发射功率,ei表示第i个位置元素为1, 其他位置元素为0, 长度为n=1, 2, …, N的列向量.式 (2) 表示总的发射功率有限,而式 (3) 表示每个阵元的发射功率相等.因此在实际发射功率约束条件下,稳健的MIMO雷达发射波形和接收滤波器联合优化模型可表示为
| $ P\left\{ \begin{array}{l} \mathop {\max }\limits_{C,\mathit{\boldsymbol{w}}} \mathop {\min }\limits_{{\theta _0} \in \theta } \frac{{{{\left| {{\alpha _0}} \right|}^2}{{\left| {{\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{a}}_r}\left( {{\theta _0}} \right) \otimes {\mathit{\boldsymbol{C}}^{\rm{H}}}{\mathit{\boldsymbol{a}}_t}\left( {{\theta _0}} \right)} \right|}^2}}}{{{\mathit{\boldsymbol{w}}^{\rm{H}}}\Sigma \left( \mathit{\boldsymbol{C}} \right)\mathit{\boldsymbol{w + }}{\mathit{\boldsymbol{w}}^{\rm{H}}}\mathit{\boldsymbol{Mw}}}},\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;{\rm{tr}}\left( {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{C}}^{\rm{H}}}} \right)E,\\ \;\;\;\;\;\mathit{\boldsymbol{e}}_i^{\rm{T}}\mathit{\boldsymbol{C}}{\left( {\mathit{\boldsymbol{e}}_i^{\rm{T}}\mathit{\boldsymbol{C}}} \right)^{\rm{H}}} = \frac{E}{{{M_t}}},i = 1,2, \cdots ,{M_t}. \end{array} \right. $ | (4) |
其中,θ表示目标可能的方向集合.由式 (4) 可知,该优化问题为关于变量C和w的非凸二次约束二次规划问题 (Quadratically Constrained Quadratic program, QCQP).为求解上述困难问题,本文采用序列优化方法[16]和半正定松弛方法[18],分别对变量C和w进行迭代优化.为利用序列优化方法求解式 (4),需要首先引入引理1.
引理1 令c=vec (CH),W=ccH、W=wwH,则输出信号SINR可表示为
| $ \begin{array}{l} {\rm{SINR}} = \frac{{{{\left| {{\alpha _0}} \right|}^2}{\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{V}}_{{\theta _0}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} V}}_{{\theta _0}}^{\rm{H}}\mathit{\boldsymbol{w}}}}{{{\mathit{\boldsymbol{w}}^{\rm{H}}}\left( {\sum\limits_{q = 1}^Q {{{\left| {{\alpha _q}} \right|}^2}{\mathit{\boldsymbol{V}}_{{\theta _q}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} V}}_{{\theta _0}}^{\rm{H}}\mathit{\boldsymbol{w}}} } \right)\mathit{\boldsymbol{w}}}} = \\ \;\;\;\;\frac{{{{\left| {{\alpha _0}} \right|}^2}{\mathit{\boldsymbol{c}}^{\rm{H}}}\mathit{\boldsymbol{V}}_{{\theta _0}}^{\rm{H}}\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{V}}_{{\theta _0}}}\mathit{\boldsymbol{c}}}}{{{\mathit{\boldsymbol{c}}^{\rm{H}}}\left( {\sum\limits_{q = 1}^Q {{{\left| {{\alpha _q}} \right|}^2}\mathit{\boldsymbol{V}}_{{\theta _q}}^{\rm{H}}\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{V}}_{{\theta _q}}}} + {\sigma ^2}\frac{{{{\left\| \mathit{\boldsymbol{w}} \right\|}^2}}}{{{{\left\| \mathit{\boldsymbol{c}} \right\|}^2}}}} \right)\mathit{\boldsymbol{c}}}}. \end{array} $ | (5) |
证明 由于CHat(θ0) 为K×1维列向量,利用公式vec (ABC)=(CT
| $ \begin{array}{l} {\left| {{\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{a}}_r}\left( {{\theta _0}} \right) \otimes {\mathit{\boldsymbol{C}}^{\rm{H}}}{\mathit{\boldsymbol{a}}_t}\left( {{\theta _0}} \right)} \right|^2} = {\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{a}}_r}\left( {{\theta _0}} \right) \otimes {\mathit{\boldsymbol{C}}^{\rm{H}}}{\mathit{\boldsymbol{a}}_t}\left( {{\theta _0}} \right) \otimes \\ \;\;\;\;\;{\mathit{\boldsymbol{I}}_K}\mathit{\boldsymbol{c}}{\left( {{\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{a}}_r}\left( {{\theta _0}} \right) \otimes \mathit{\boldsymbol{a}}_t^{\rm{H}}\left( {{\theta _0}} \right) \otimes {\mathit{\boldsymbol{I}}_K}\mathit{\boldsymbol{c}}} \right)^{\rm{H}}} = \\ \;\;\;\;\;{\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{V}}_{{\theta _0}}}\mathit{\boldsymbol{c}}{\mathit{\boldsymbol{c}}^{\rm{H}}}\mathit{\boldsymbol{V}}_{{\theta _0}}^{\rm{H}}\mathit{\boldsymbol{w}} = {\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{V}}_{{\theta _0}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} V}}_{{\theta _0}}^{\rm{H}}\mathit{\boldsymbol{w}} = \\ \;\;\;\;\;{\mathit{\boldsymbol{c}}^{\rm{H}}}\mathit{\boldsymbol{V}}_{{\theta _0}}^{\rm{H}}\mathit{\boldsymbol{w}}{\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{V}}_{{\theta _0}}}\mathit{\boldsymbol{c = }}{\mathit{\boldsymbol{c}}^{\rm{H}}}\mathit{\boldsymbol{V}}_{{\theta _0}}^{\rm{H}}\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{V}}_{{\theta _0}}}\mathit{\boldsymbol{c}}, \end{array} $ |
其中,Vθ0=ar(θ0)
| $ \begin{array}{l} {\mathit{\boldsymbol{w}}^{\rm{H}}}\Sigma \left( \mathit{\boldsymbol{C}} \right)\mathit{\boldsymbol{w + }}{\mathit{\boldsymbol{w}}^{\rm{H}}}\mathit{\boldsymbol{Mw}} = {\mathit{\boldsymbol{w}}^{\rm{H}}}\left( {\sum\limits_{q = 1}^Q {{{\left| {{\alpha _q}} \right|}^2}{\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{V}}_{{\theta _q}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} V}}_{{\theta _q}}^{\rm{H}}} + } \right.\\ \;\;\;\;\;\left. {{\sigma ^2}{\mathit{\boldsymbol{I}}_{{M_r}K}}} \right)\mathit{\boldsymbol{w = }}{\mathit{\boldsymbol{c}}^{\rm{H}}}\left( {\sum\limits_{q = 1}^Q {{{\left| {{\alpha _q}} \right|}^2}\mathit{\boldsymbol{V}}_{{\theta _q}}^{\rm{H}}\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{V}}_{{\theta _q}}}} + } \right.\\ \;\;\;\;\;\left. {{\sigma ^2}\frac{{{{\left\| \mathit{\boldsymbol{w}} \right\|}^2}}}{{{{\left\| \mathit{\boldsymbol{c}} \right\|}^2}}}} \right)\mathit{\boldsymbol{c}}. \end{array} $ |
引理1得证.
根据矩阵迹运算特性tr (AB)=vec (A)Hvec (B) 及式 (5),可将P转化为
| $ \tilde P\left\{ \begin{array}{l} \mathop {\max }\limits_{\mathit{\Psi ,W}} \mathop {\min }\limits_{{\theta _0} \in \mathit{\Theta }} \frac{{{{\left| {{\alpha _0}} \right|}^2}{\rm{tr}}\left( {{\mathit{\boldsymbol{V}}_{{\theta _0}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} V}}_{{\theta _0}}^{\rm{H}}\mathit{\boldsymbol{W}}} \right)}}{{\sum\limits_{q = 1}^Q {{{\left| {{\alpha _q}} \right|}^2}{\rm{tr}}\left( {{\mathit{\boldsymbol{V}}_{{\theta _q}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} V}}_{{\theta _q}}^{\rm{H}}\mathit{\boldsymbol{W}}} \right)} + {\sigma ^2}{\rm{tr}}\left( \mathit{\boldsymbol{W}} \right)}},\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;\;\;\;{\rm{tr}}\left( \mathit{\boldsymbol{ \boldsymbol{\varPsi} }} \right) = E,\\ \;\;\;\;\;\;\;\;\;\;\;{\rm{tr}}\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{B}}_i}} \right) = \frac{E}{{{M_t}}},i = 1,2, \cdots ,{M_t},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{ \boldsymbol{\varPsi} }} \ge 0,{\rm{rank}}\left( \mathit{\boldsymbol{ \boldsymbol{\varPsi} }} \right) = 1,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{W}} \ge 0,{\rm{rank}}\left( \mathit{\boldsymbol{W}} \right) = 1. \end{array} \right. $ |
其中,Bi=IK
| $ \bar P\left\{ \begin{array}{l} \mathop {\max }\limits_{\mathit{\Psi ,W}} \mathop {\min }\limits_{{\theta _0} \in \mathit{\Theta }} \frac{{{{\left| {{\alpha _0}} \right|}^2}{\rm{tr}}\left( {{\mathit{\boldsymbol{V}}_{{\theta _0}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} V}}_{{\theta _0}}^{\rm{H}}\mathit{\boldsymbol{W}}} \right)}}{{\sum\limits_{q = 1}^Q {{{\left| {{\alpha _q}} \right|}^2}{\rm{tr}}\left( {{\mathit{\boldsymbol{V}}_{{\theta _q}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} V}}_{{\theta _q}}^{\rm{H}}\mathit{\boldsymbol{W}}} \right)} + {\sigma ^2}{\rm{tr}}\left( \mathit{\boldsymbol{W}} \right)}},\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;\;\;\;{\rm{tr}}\left( \mathit{\boldsymbol{ \boldsymbol{\varPsi} }} \right) = E,\\ \;\;\;\;\;\;\;\;\;\;\;{\rm{tr}}\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{B}}_i}} \right) = \frac{E}{{{M_t}}},i = 1,2, \cdots ,{M_t},\\ \;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{ \boldsymbol{\varPsi} }} \ge 0,W \ge 0. \end{array} \right. $ |
问题P的目标函数仍为关于W和Ψ的非凸优化问题,针对该类问题可以采用序列优化思想,将问题分解为分别关于W和Ψ的子优化问题,即假设W/Ψ固定,利用W/Ψ优化计算Ψ/W,再根据优化结果Ψ/W进一步计算优化W/Ψ.
2.1 固定W优化Ψ当W固定时,定义t为一辅助变量,利用式 (5) 及矩阵迹运算特性tr (Ψ)=‖c‖2, tr (W)=‖w‖2,可将P等价转化为
| $ {P_\mathit{\Psi }}\left\{ \begin{array}{l} \mathop {\max }\limits_\mathit{\Psi } \frac{t}{{\sum\limits_{q = 1}^Q {{{\left| {{\alpha _q}} \right|}^2}{\rm{tr}}\left( {\mathit{\boldsymbol{V}}_{{\theta _q}}^{\rm{H}}\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{V}}_{{\theta _q}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}} \right) + {\sigma ^2}{\rm{tr}}\left( \mathit{\boldsymbol{W}} \right)} }},\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;{\left| {{\alpha _0}} \right|^2}{\rm{tr}}\left( {\mathit{\boldsymbol{V}}_{{\theta _q}}^{\rm{H}}\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{V}}_{{\theta _q}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}} \right) \ge t,\;\;\forall {\theta _0} \in \mathit{\Theta ,}\\ \;\;\;\;\;{\rm{tr}}\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{B}}_i}} \right)\frac{E}{{{M_t}}},i = 1,2, \cdots ,{M_t},\\ \;\;\;\;\;{\rm{tr}}\left( \mathit{\boldsymbol{ \boldsymbol{\varPsi} }} \right) = E,\mathit{\boldsymbol{ \boldsymbol{\varPsi} }} \ge 0. \end{array} \right. $ | (6) |
虽然式 (6) 目标函数仍为非凸的,但是由于PΨ为一般的线性规划问题,因此可以利用类凸优化方法对问题PΨ进行求解[17],但是该方法在每次迭代过程中需要对t值遍历以计算最优矩阵Ψ,计算复杂度较高.针对该问题,本文利用Charnes-Cooper转换方法[19],通过引入附加变量r并令Y=rΨ, t=rt,将问题PΨ转化为
| $ {{\tilde P}_\mathit{\Psi }}\left\{ \begin{array}{l} \mathop {\max }\limits_{Y,\tilde t,r} \tilde t,\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\sum\limits_{q = 1}^Q {{{\left| {{\alpha _q}} \right|}^2}{\rm{tr}}\left( {\mathit{\boldsymbol{V}}_{{\theta _q}}^{\rm{H}}\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{V}}_{{\theta _q}}}\mathit{\boldsymbol{Y}}} \right) + r{\sigma ^2}{\rm{tr}}\left( \mathit{\boldsymbol{W}} \right)} = 1,\\ \;\;\;\;\;{\left| {{\alpha _0}} \right|^2}{\rm{tr}}\left( {\mathit{\boldsymbol{V}}_{{\theta _q}}^{\rm{H}}\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{V}}_{{\theta _q}}}\mathit{\boldsymbol{Y}}} \right) \ge \tilde t,\;\;\forall {\theta _0} \in \mathit{\Theta ,}\\ \;\;\;\;\;{\rm{tr}}\left( {\mathit{\boldsymbol{Y}}{\mathit{\boldsymbol{B}}_i}} \right)\frac{{rE}}{{{M_t}}},i = 1,2, \cdots ,{M_t},\\ \;\;\;\;\;{\rm{tr}}\left( \mathit{\boldsymbol{Y}} \right) = rE,\mathit{\boldsymbol{Y}} \ge 0. \end{array} \right. $ | (7) |
为证明问题PΨ和
引理2 优化问题
证明 假设 (Ψ*, t*) 为PΨ的最优解,定义Ω(PΨ)、Ω(
| $ \begin{array}{l} \left( {\mathit{\boldsymbol{Y}},\tilde t,r} \right) = \left( {\frac{{{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}^ * }}}{{\sum\limits_{q = 1}^Q {{{\left| {{\alpha _q}} \right|}^2}{\rm{tr}}\left( {\mathit{\boldsymbol{V}}_{{\theta _q}}^{\rm{H}}\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{V}}_{{\theta _q}}}\mathit{\boldsymbol{Y}}} \right) + {\sigma ^2}{\rm{tr}}\left( \mathit{\boldsymbol{W}} \right)} }},} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\frac{t}{{\sum\limits_{q = 1}^Q {{{\left| {{\alpha _q}} \right|}^2}{\rm{tr}}\left( {\mathit{\boldsymbol{V}}_{{\theta _q}}^{\rm{H}}\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{V}}_{{\theta _q}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}} \right) + {\sigma ^2}{\rm{tr}}\left( \mathit{\boldsymbol{W}} \right)} }},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\frac{1}{{\sum\limits_{q = 1}^Q {{{\left| {{\alpha _q}} \right|}^2}{\rm{tr}}\left( {\mathit{\boldsymbol{V}}_{{\theta _q}}^{\rm{H}}\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{V}}_{{\theta _q}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}} \right) + {\sigma ^2}{\rm{tr}}\left( \mathit{\boldsymbol{W}} \right)} }}} \right). \end{array} $ |
且 (Y,
| $ \frac{{{t^ * }}}{{\sum\limits_{q = 1}^Q {{{\left| {{\alpha _q}} \right|}^2}{\rm{tr}}\left( {\mathit{\boldsymbol{V}}_{{\theta _q}}^{\rm{H}}\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{V}}_{{\theta _q}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}} \right) + {\sigma ^2}{\rm{tr}}\left( \mathit{\boldsymbol{W}} \right)} }}. $ |
与PΨ最优解所对应的目标函数值相同,因此可得
| $ \mathit{\Omega }\left( {{P_\mathit{\Psi }}} \right) \le \mathit{\Omega }\left( {{{\tilde P}_\mathit{\Psi }}} \right). $ | (8) |
定义 (Y*,
| $ \mathit{\Omega }\left( {{P_\mathit{\Psi }}} \right) \ge \mathit{\Omega }\left( {{{\tilde P}_\mathit{\Psi }}} \right). $ | (9) |
根据式 (8)、(9) 可得Ω(PΨ)=Ω(
通过Charnes-Cooper转换之后,非凸的分式规划问题PΨ转化为关于变量Y、
假设Ψ固定,对W进行优化,通过引入变量ξ,
| $ {P_W}\left\{ \begin{array}{l} \mathop {\max }\limits_{W,\zeta } \frac{\zeta }{{\sum\limits_{q = 1}^Q {{{\left| {{\alpha _q}} \right|}^2}{\rm{tr}}\left( {\mathit{\boldsymbol{V}}_{{\theta _q}}^{\rm{H}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{V}}_{{\theta _q}}}\mathit{\boldsymbol{W}}} \right) + {\sigma ^2}{\rm{tr}}\left( \mathit{\boldsymbol{W}} \right)} }},\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;{\left| {{\alpha _0}} \right|^2}{\rm{tr}}\left( {{\mathit{\boldsymbol{V}}_{{\theta _0}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{V}}_{{\theta _q}}}\mathit{\boldsymbol{W}}} \right) \ge \zeta ,\;\;\forall {\theta _0} \in \mathit{\Theta ,}\\ \;\;\;\;\;\;\mathit{\boldsymbol{W}} \ge 0,\\ \;\;\;\;\;\;{\rm{rank}}\left( \mathit{\boldsymbol{W}} \right) = 1. \end{array} \right. $ |
利用
| $ {{\tilde P}_W}\left\{ \begin{array}{l} \mathop {\max }\limits_{W,\zeta } \zeta ,\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;{\left| {{\alpha _0}} \right|^2}{\rm{tr}}\left( {{\mathit{\boldsymbol{V}}_{{\theta _0}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} V}}_{{\theta _0}}^{\rm{H}}\mathit{\boldsymbol{W}}} \right) \ge \zeta ,\;\;\forall {\theta _0} \in \mathit{\Theta ,}\\ \;\;\;\;\;\;\sum\limits_{q = 1}^Q {{{\left| {{\alpha _q}} \right|}^2}{\rm{tr}}\left( {\mathit{\boldsymbol{V}}_{{\theta _q}}^{\rm{H}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{V}}_{{\theta _q}}}\mathit{\boldsymbol{W}}} \right) + {\sigma ^2}{\rm{tr}}\left( \mathit{\boldsymbol{W}} \right){\rm{ = }}1} ,\\ \;\;\;\;\;\;\mathit{\boldsymbol{W}} \ge 0. \end{array} \right. $ | (10) |
利用凸优化求解方法可以在多项式时间内求解问题
Step 1 选择随机向量w,初始化矩阵W;
Step 2 利用W通过式 (7) 计算求解Ψ;
Step 3 利用Ψ通过式 (10) 计算求解W;
Step 4 重复Step 1和Step 2,直到第m次优化后输出SINR(m)与第 (m-1) 次优化输出SINR(m-1)之间满足|SINR(m)-SINR(m-1)|≤μ,其中μ预先设置的截止因子,则停止优化输出W和Ψ.
2.3 根据协方差矩阵计算发射加权向量和接收滤波器利用序列优化方法分别计算得到最优协方差矩阵Ψ*和W*后,接下来则需要根据W*、Ψ*求解具体的发射信号加权向量c和接收滤波器w.由于本文针对发射信号加权向量进行优化,因此避免了由给定的信号协方差矩阵求解具体信号这一困难问题,c与w的求解方法完全相同,本节仅以w为例给出具体计算过程.
若rank (W*)=1,则可以通过矩阵特征值分解直接求得w,但是由于在优化求解过程中利用了半正定松弛,因此所得优化矩阵W*并不一定满足rank (W*)=1的约束条件.若rank (W*)≥2,则需利用随机化方法[18]求解秩近似为1的次优化向量w,具体计算过程为:任意选取M个随机向量wm,且wm服从均值为0, 方差为W*的复高斯正态分布,即wm~NC(0, W*),m=1, 2, …, m,M为随机化实验次数.对每一个随机向量wm,在最优协方差矩阵Ψ*条件下计算不确定集Θ内最差情况下的输出信号SINR,即
| $ {\rm{SIN}}{{\rm{R}}_m} = \mathop {\min }\limits_{{\theta _0} \in \mathit{\Theta }} \frac{{{{\left| {{\alpha _0}} \right|}^2}\mathit{\boldsymbol{w}}_m^{\rm{H}}{\mathit{\boldsymbol{V}}_{{\theta _0}}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}^ * }\mathit{\boldsymbol{V}}_{{\theta _0}}^{\rm{H}}{\mathit{\boldsymbol{w}}_m}}}{{\mathit{\boldsymbol{w}}_m^{\rm{H}}\left( {\sum\limits_{q = 1}^Q {{{\left| {{\alpha _q}} \right|}^2}{\mathit{\boldsymbol{V}}_{{\theta _q}}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}^ * }\mathit{\boldsymbol{V}}_{{\theta _q}}^{\rm{H}} + {\sigma ^2}{\mathit{\boldsymbol{I}}_{M,K}}} } \right){\mathit{\boldsymbol{w}}_m}}}. $ |
则序列{SINRm}中最大值所对应的wm即可作为接收滤波器的最优解w*.同理可计算得到最终发射加权向量c*.
2.4 算法性能分析为证明本文所提MIMO雷达发射波形和接收滤波器联合优化设计的可行性和有效性,本节将对所提方法计算复杂度以及算法收敛性进行证明分析.由算法1可知,所提联合优化算法总的计算复杂度主要由式 (7) 和式 (9) 的计算复杂度以及迭代次数所决定.为清晰直观地体现出本文所提算法在计算量上的优势,将本文所提方法与文献[14]及文献[17]所提方法每次迭代计算复杂度以表格形式给出,具体如表 1所示.在实际应用中由于选择的正交基带信号个数小于发射阵元数且远小于信号编码长度, 即K≤Mt≤N,因此本文所提方法在每次迭代过程中发射波形和接收滤波器计算复杂度均小于文献[14]所提方法.而文献[17]由于未考虑方向失配影响,在每次迭代中计算接收滤波器向量时直接利用自适应波束形成MVDR算法,虽然相比本文所提算法计算复杂度较小,但是在每次迭代过程中都需要利用随机向量合成方法由优化后的协方差矩阵Ψ求解具体的加权向量,而且在求解优化矩阵Ψ的过程中采用类凸优化方法需要对所有可能t值进行遍历,因此每次迭代过程中发射波形优化计算复杂度为O(Lt(MtK)3.5)+O(M(MtK)2),远大于本文所提方法.因此相比于现有方法, 本文所提算法具有较高的计算效率.
| 表 1 不同算法计算复杂度比较 Table 1 Computational burden comparison of different methods |
为证明所提算法的可行性,接下来对算法收敛性进行分析证明.本文将非凸优化问题P通过松弛变换转化为两个凸的半正定规划问题
| $ \begin{array}{l} \mathop {\min }\limits_{{\theta _0} \in \mathit{\Theta }} {\rm{SINR}}\left( {{\theta _0}} \right) \le \frac{{{{\left| {{\alpha _0}} \right|}^2}{\mathit{\boldsymbol{w}}^{\rm{H}}}{\mathit{\boldsymbol{V}}_{{\theta _0}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} V}}_{{\theta _0}}^{\rm{H}}\mathit{\boldsymbol{w}}}}{{{\mathit{\boldsymbol{w}}^{\rm{H}}}\left( {\sum\limits_{q = 1}^Q {{{\left| {{\alpha _q}} \right|}^2}{\mathit{\boldsymbol{V}}_{{\theta _q}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} V}}_{{\theta _q}}^{\rm{H}} + {\sigma ^2}{\mathit{\boldsymbol{I}}_{M,K}}} } \right)\mathit{\boldsymbol{w}}}} \le \\ \;\;\;\frac{{{{\left| {{\alpha _0}} \right|}^2}\left\| \mathit{\boldsymbol{w}} \right\|{\lambda _{\max }}\left( {{\mathit{\boldsymbol{V}}_{{\theta _0}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} V}}_{{\theta _0}}^{\rm{H}}} \right)}}{{{\sigma ^2}{\rm{tr}}\left( \mathit{\boldsymbol{W}} \right)}} \le \frac{{{{\left| {{\alpha _0}} \right|}^2}{\rm{tr}}\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} V}}_{{\theta _0}}^{\rm{H}}{\mathit{\boldsymbol{V}}_{{\theta _0}}}} \right)}}{{{\sigma ^2}}} \le \\ \;\;\;\frac{{{{\left| {{\alpha _0}} \right|}^2}{M_t}KE}}{{{\sigma ^2}}}. \end{array} $ |
其中,λmax(Vθ0ΨVθ0H) 表示计算矩阵Vθ0ΨVθ0H的最大特征值,因此序列{
设收发共置MIMO雷达发射阵元数为Mt=10,接收阵元数为Mr=8,且阵元间距为半波长.假设目标位置方向为θ0=0°,目标方向不确定集范围为Θ=[-6°, 6°],目标信号信噪比RSN=10 dB.设有6个相互独立的杂波反射点,方向分别为-45°、-30°、-15°、20°、30°和50°,每个杂波反射信号杂噪比均为INR=40 dB,雷达系统噪声为高斯白噪声,算法迭代截止因子μ=0.01,信号合成算法中随机化实验次数N=1 000.为验证所提算法的有效性,实验将对雷达发射方向图、算法稳健性以及算法输出SINR进行仿真分析.
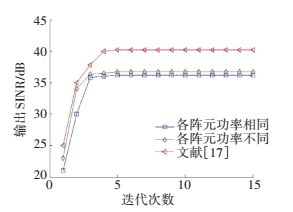
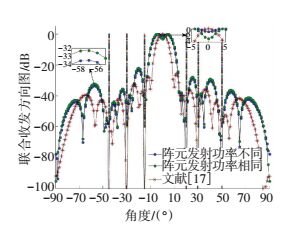
设正交基带信号个数K=8其他仿真条件不变,分别对各阵元发射功率相同的稳健方法、各阵元发射功率不同的稳健方法和文献[17]所提方法进行对比. 图 1为在不考虑误差的情况下,3种不同算法求解优化问题时的迭代次数.由图 1可知, 本文所提算法能够较快收敛到最优解,得到最优加权向量和接收滤波器的协方差矩阵. 图 2为3种不同方法在杂波条件下的收发联合方向图,其中虚线为杂波方向.由图 2可知, 本文所提稳健的发射波形和接收滤波器联合优化设计方法能够有效抑制杂波,而且对可能的目标信号来波方向形成一个较宽的主瓣,从而有效提高算法稳健性,克服了因目标期望信号方向失配而造成的输出信号SINR急剧下降的情况.而且由图 2可以看出,各阵元发射功率不同情况下所形成的收发联合方向图相比于各阵元发射功率相同时所形成的联合方向图,具有更低的旁瓣和更为平稳的主瓣,这是因为阵元发射功率不同可以增加波形优化自由度,从而提高系统性能,但是不同阵元之间较大的发射功率差异提高了对系统硬件的要求.
|
图 1 算法输出SINR随迭代次数收敛情况 Figure 1 The output SINR versus iteration number |
|
图 2 不同算法收发联合方向 Figure 2 The joint beampatterns of different methods |
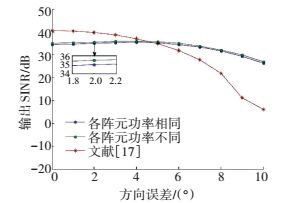
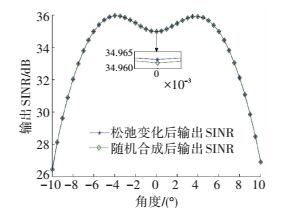
进一步分析对比算法对目标信号方向误差的稳健性,设目标信号方向误差取值范围为[0°, 10°],其他条件不变,算法输出SINR随方向误差的变化情况见图 3.当方向误差较小时,文献[17]所提方法性能优于本文所提稳健算法,但是随着误差的增大性能急剧下降;而本文所提方法在方向误差一定的范围内输出SINR变化缓慢,因此具有较好的稳健性. 图 4则对比分析了算法中信号合成前后系统输出SINR.由图 4可知,利用随机化向量合成方法求得具体发射加权矩阵和接收滤波器后所得SINR,与直接利用所得优化矩阵Ψ*和W*所得输出SINR几乎完全相同,因此利用随机化向量合成方法求解具体的发射加权矩阵和接收滤波器不会对系统性能造成较大影响.
|
图 3 输出SINR随目标信号方向误差的变化情况 Figure 3 The output SINR versus the DOA error of target signal |
|
图 4 信号合成前后性能对比 Figure 4 Performance comparison of signal before and after synthesis |
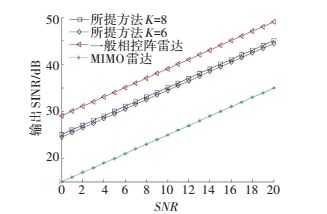
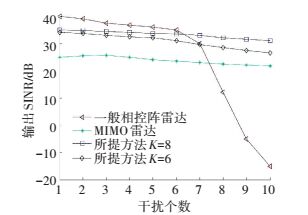
为验证分析算法输出SINR性能,设目标信号RSN变化范围为[0, 20 dB],正交基带信号个数分别为6和8,其他条件不变.在不考虑方向误差的情况下,系统输出SINR的变化情况如图 5所示.当杂波信号个数小于相控阵雷达接收阵列自由度时,所提方法相较于一般MIMO雷达具有较高的输出SINR,但是随着杂波干扰个数的增加,相控阵雷达性能急剧下降,如图 6所示.而本文所提方法由于对发射信号和接收滤波器联合优化设计,从发射端和接收端联合优化抑制杂波,因此系统自由度更高, 能够有效抑制多杂波情况.而且相比于一般全向MIMO雷达,利用发射加权矩阵处理后每个阵元发射相关信号,系统具有一定的发射增益,因此输出SINR介于一般相控阵和全向MIMO雷达之间.
|
图 5 不同雷达输出SINR随RSN的变化情况 Figure 5 The output SINR of different radar versus input RSN |
|
图 6 不同雷达输出SINR随杂波个数变化情况 Figure 6 The output SINR of different radar versus the number of interferences |
本文针对杂波条件下目标期望信号不确定时雷达输出SINR较低的情况,提出一种稳健的MIMO雷达发射波形和接收滤波器联合优化设计方法.首先针对所提出的在不确定集范围内对发射加权矩阵和接收滤波器进行联合优化的Max-min非凸困难问题,通过序列优化转化为对发射加权矩阵和接收滤波器的迭代优化问题; 然后利用Charnes-Cooper转换和半正定松弛将非凸的迭代优化转化为易于求解的凸优化问题,分析了所提算法的计算复杂度并对算法收敛性和可行性给出了证明; 最后通过对所提算法的收发联合方向图、稳健性及不同条件下输出SINR性能进行仿真对比,进一步证明了算法有效性以及实际的工程应用价值.
| [1] | STOCIA P, LI J, XIE Y. On probing signal design for MIMO radar[J]. IEEE Transactions on Signal Processing, 2007, 55(8): 4151-4161. DOI: 10.1109/TSP.2007.894398 |
| [2] | FUHRMANN DR, ANTONIO G S. Transmit beamforming for MIMO radar systems using signal cross-correlation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(1): 171-186. DOI: 10.1109/TAES.2008.4516997 |
| [3] | GONG P, SHAO Z, TU G, et al. Transmit beampattern design based on convex optimization for MIMO radar systems[J]. Signal Processing, 2014, 94(1): 195-201. DOI: 10.1016/j.sigpro.2013.06.021 |
| [4] | IMANI S, GHOTASHI S A, BOLHASANI M. SINR maximization on colocated MIMO radars using transmit covariance matrix[J]. Signal Processing, 2016, 119(C): 128-135. DOI: 10.1016/j.sigpro.2015.07.011 |
| [5] | KHABBAZIBASMENJ A, HASSANIEN A, VOROBYOV S A, et al. Efficient transmit beamspace design for search-free based DOA estimation in MIMO radar[J]. IEEE Transactions on Signal Processing, 2014, 62(6): 1490-1500. DOI: 10.1109/TSP.2014.2299513 |
| [6] | HASSANIEN A, VOROBYOV S A. Transmit energy focusing for DOA estimation in MIMO radar with colocated antennas[J]. IEEE Transactions on Signal Processing, 2011, 59(6): 2669-2682. DOI: 10.1109/TSP.2011.2125960 |
| [7] | AHMED S, ALOUINI M S. MIMO radar transmit beampattern design without synthesising the covariance matrix[J]. IEEE Transactions on Signal Processing, 2014, 62(9): 2278-2289. DOI: 10.1109/TSP.2014.2310435 |
| [8] |
黄中瑞, 单凉, 陈明建, 等. 一种新的MIMO雷达发射波形设计方法[J].
电子与信息学报, 2016, 38(5): 1026-1033.
HUANG Zhongrui, SHAN Liang, CHEN Mingjian, et al. A new method for the design of transmit waveform of MIMO radar[J]. Journal of Electronics and Information Technology, 2016, 38(5): 1026-1033. DOI: 10.11999/JEIT150758 |
| [9] | BENJAMIN F. On transmit beamforming for mimo radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(4): 3376-3388. DOI: 10.1109/TAES.2012.6324717 |
| [10] | LI Y, VOROBYOV S A, KOIVUNEN V. Ambiguity function of the transmit beamspace-based MIMO radar[J]. IEEE Transactions on Signal Processing, 2015, 63(17): 4445-4457. DOI: 10.1109/TSP.2015.2439241 |
| [11] | LIU J, LI H, HIMED B. Joint optimization of transmit and receive beamforming in active arrays[J]. IEEE Signal Processing Letters, 2014, 21(1): 39-42. DOI: 10.1109/LSP.2013.2289325 |
| [12] | CHEN Z, LI H, CUI G, RANGASWAMY M. Adaptive transmit and receive beamforming for interference mitigation[J]. IEEE Signal Processing Letters, 2014, 21(2): 235-239. DOI: 10.1109/LSP.2014.2298497 |
| [13] | SEYYED M K, AUGUSTO A, ANTONIO D M, et al. Robust transmit code and receive filter design for extended targets in clutter[J]. IEEE Transactions on Signal Processing, 2015, 63(8): 1965-1976. DOI: 10.1109/TSP.2015.2404301 |
| [14] | SEYYED M K, AUGUSTO A, ANTONIO D M, et al. Knowledge-based design of space-time transmit code and receive filter for a multiple-input-multiple-output radar in signal-dependent interference[J]. IET Radar, Sonar and Navigation, 2015, 9(8): 1124-1135. DOI: 10.1049/iet-rsn.2014.0527 |
| [15] | SADJAD I, SEYED A G. Sequential quasi-convex-based algorithm for waveform design in colocated multiple-input-multiple-output radars[J]. IET Signal Processing, 2015, 10(3): 309-317. DOI: 10.1049/iet-spr.2015.0181 |
| [16] | SEYYED M K, MAJTABA R, MOHAMMAD M N, et al. Design of multiple-input-multiple-output transmit waveform and receive filter for extended target detection[J]. IET Radar, Sonar and Navigation, 2015, 9(9): 1345-1353. DOI: 10.1049/iet-rsn.2015.0063 |
| [17] | SADJAD I, SEYED A G. Transmit signal and receive filter design in co-located MIMO radar using a transmit weighting matrix[J]. IEEE Signal Processing Letters, 2015, 22(10): 1521-1524. DOI: 10.1109/LSP.2015.2411676 |
| [18] | LUO Z Q, MA W K, SO A C, et al. Semidefinite relaxation of quadratic optimization problems[J]. IEEE Signal Process Magazine, 2010, 27(3): 20-34. DOI: 10.1109/MSP.2010.936019 |
| [19] | CHARNES A, COOPER W W. Programming with linear fractional functionals[J]. Naval Research Logistics Quarterly, 1962, 9(3): 181-186. DOI: 10.1002/nav.3800090303 |
 2017, Vol. 49
2017, Vol. 49


