蒸发波导是由水汽蒸发引起的大气湿度随高度锐减的大气现象,它会造成电磁波的异常传播,并减小电磁波的海上传播损耗.蒸发波导具有较高的发生概率,所以广泛应用于超视距雷达探测[1].然而大气参数会随时间和空间不断变化,超视距雷达的探测威力也将发生变化.雷达威力的预测可为作战舰艇提供辅助决策,使其合理把握雷达开关机时间,提高生存能力.通过蒸发波导计算雷达探测威力,首先需要测量海上的水文气象参数,包括风速、湿度、气压以及海表温度,然后通过波导模型得到海上大气折射率廓线[2-3],再通过电磁波传播模型计算雷达电波传播损耗,最终预测出雷达的探测威力[2, 4].海表温度的测量影响着预报结果的准确程度,是整个预报系统中的难点.
海表温度的测量与海水温度测量不同,是测量海水与空气接触部分的水温.因蒸发作用和热交换作用的存在,海表温度与海水温度存在一定区别[5].与其他接触式温度传感器相比,利用红外传感器测量海水温度具有独特的优势[6-7]:一是在红外波段,海水的透射率很低,红外传感器测量的温度为海表面以下几毫米的海水温度,与理论上的海表温度十分接近[8];二是红外传感器与海面不发生接触,不会因热传导而改变被测海水的温度.但因海表面的红外辐射率小于1,加上天空背景的干扰,红外传感器的测量温度与真实的海温之间存在偏差,会使得测量温度低于真实温度.
本文针对红外传感器温度测量的偏差,结合海面与天空的红外辐射模型,提出一种基于红外传感器的海表温度修正方法,并将其应用到超视距雷达的威力预报中,验证了方法的有效性.
1 红外温度测量及影响因素 1.1 红外温度测量模型红外传感器通过测量被测物体的红外辐射,能在不接触物体的条件下,实现温度的测量.以热释电型红外温度传感器为例,传感器利用温差电效应,通过测量因温差引起的电压值U0,得到被测物的辐射温度Tm,即传感器的测量结果. U0和Tm的关系可表示为[9]
| $ {U_0} = C\left( {T_m^4 - T_{\rm{a}}^4} \right). $ |
式中:Ta表示传感器自身的温度,单位为华氏温度;C为与传感器自身结构相关的参数.
测量结果Tm4与传感器探头受到的红外辐射照度Em成线性关系.若测量范围内只存在被测物而不包含其他干扰物,Tm和Em之间的关系可表示为
| $ \begin{array}{l} {E_{\rm{m}}} = \int_{{\lambda _1}}^{{\lambda _2}} {\int\limits_\mathit{\Omega } {{L_{\rm{b}}}\left( {{T_{\rm{m}}},\lambda } \right)\cos \beta {\rm{d}}\mathit{\Omega }{\rm{d}}\lambda } } = \\ \;\;\;\;\;\;\;\;\;\pi {\sin ^2}\alpha \int_{{\lambda _1}}^{{\lambda _2}} {{L_{\rm{b}}}\left( {\lambda ,{T_{\rm{m}}}} \right){\rm{d}}\lambda } . \end{array} $ | (1) |
式中:Lb(Tm, λ) 表示辐射温度为Tm,波长为λ时黑体的辐射亮度;α表示传感器的测量半角;Ω表示传感器测量半角范围内的空间角,测量过程中需保证在Ω角度范围内仅包含被测物体,dΩ=sin βdβdγ;β表示在空间角为dΩ时,红外辐射方向
为研究红外传感器在舰船条件下海表温度的测量精度,通过实验研究了高度和倾角对测量结果的影响.实验中发现高度的变化对测量结果基本没有影响,但倾角的增大会导致测量误差的增大.这一测量误差,实际为海表面红外辐射的物理过程造成的测量温度和真实温度之间的偏差.
红外传感器的测量结果实际为等效黑体的温度,但海面的辐射率小于黑体的辐射率,即小于1,并且辐射率会随辐射角度的增大而降低,因此测量的海表温度将小于实际海表温度.同时,辐射角度增大时海面的反射率会增大,天空背景的干扰也将增大.
因此红外传感器测量温度,并非真实海表温度.通过测量的温度获取真实的海表温度,需要对海面的辐射率和反射率进行建模,测量并补偿天空温度.
2 海表面温度测量模型海面的辐射率变化及反射的天空温度会造成海表面的测量温度存在偏差,在此将对海表面的红外辐射和反射的天空辐射进行建模,分析测量偏差的分布概率.
2.1 海表面的红外辐射模型针对海表面的辐射率问题,常用的模型是平静海面模型,该模型考虑了辐射方向变化对海面红外辐射率的影响,可表示为[6, 10]
| $ \varepsilon \left( \theta \right) = 0.98\left[ {1 - {{\left( {1 - \cos \theta } \right)}^5}} \right], $ |
式中θ表示海面的辐射方向与Z轴的夹角.
该模型忽略了海面波浪的起伏对测量结果的影响.为获得更准确的海面辐射模型,需要考虑海浪影响. Charles Cox及Walter Munk给出了海浪坡度的分布概率,其概率密度函数为[6, 10]
| $ \left\{ \begin{array}{l} f\left( {{s_x},{s_y}} \right) = \frac{1}{{2\pi {\sigma ^2}}}\exp \left( { - \frac{{s_x^2 + s_y^2}}{{2{\sigma ^2}}}} \right),\\ 2{\sigma ^2} = 0.003 + 0.005\;12 \times v. \end{array} \right. $ | (2) |
式中:sx和sy分别表示x方向和y方向海浪的坡度分量,v表示12.5 m高度处的风速.若
| $ \begin{array}{*{20}{c}} {{s_x} = - \tan {\theta _n}\cos {\varphi _n},}\\ {{s_y} = - \tan {\theta _n}\cos {\varphi _n},}\\ {\cos \chi = \cos {\theta _n}\cos {\theta _e} + \cos \left( {{\varphi _e} - {\varphi _n}} \right)\sin {\theta _n}\sin {\theta _e}.} \end{array} $ | (3) |
通过变量代换,式 (2) 可写为
| $ f\left( {{u_n},{\varphi _n}} \right) = \frac{{u_n^{ - 3}}}{{2\pi {\sigma ^2}}}\exp \left( {\frac{{1 - u_n^{ - 2}}}{{2{\sigma ^2}}}} \right), $ | (4) |
式中un等于cosθn.在
| $ \begin{array}{l} {{\bar \varepsilon }_\lambda }\left( {{\theta _e},{\varphi _e}} \right) = \frac{1}{{\cos {\theta _e}}}\int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {{\varepsilon _\lambda }\left( \chi \right)\cos \chi } } .\\ \sec {\theta _n}P\left( {{s_{x,}}{s_y}} \right){\rm{d}}{s_x}{\rm{d}}{s_y} = \frac{1}{{\cos {\theta _e}}}\int_0^1 {\int_0^{2\pi } {{\varepsilon _\lambda }\left( \chi \right)} } .\\ \cos \chi u_0^{ - 1}f\left( {{u_n},{\varphi _n}} \right){\rm{d}}{u_n}{\rm{d}}{\varphi _n}. \end{array} $ | (5) |
因此,对于辐射波长为λ,在
| $ {L_{{\rm{sea}}}}\left( {{T_{{\rm{sea}}}},\lambda ,{\theta _e},{\varphi _e}} \right) = {{\bar \varepsilon }_\lambda }\left( {{\theta _e},{\varphi _e}} \right)\frac{{{M_{\rm{b}}}\left( {{T_{{\rm{sea}}}},\lambda } \right)}}{\pi }, $ |
式中Mb(Tsea, λ) 表示表温度为Tsea时,海面的辐射出射度,海温取华氏温度.
2.2 天空反射模型天空的红外辐射分为晴天无云、有云和下雨3种情况.无云时多由太阳光的散射和大气热辐射组成,有云或下雨时多为云团的水汽或雨水造成的红外热辐射.天空的红外辐射可视为黑体的红外辐射,并可采用45 °天顶角的辐射代替[7].太阳的红外辐射也会对传感器的测量结果造成影响,其辐射方向可通过时间和传感器的经纬度计算得到[6],因此入射方向为
| $ {L_{{\rm{sky}}}}\left( {{\theta _i},{\varphi _i}} \right) = \frac{{\sigma T_{{\rm{sky}}}^4}}{\pi } + {L_{{\rm{sun}}}}\left( {{\theta _i},{\varphi _i}} \right). $ |
式中:σ表示史蒂芬-玻尔兹曼常数;Tsky表示天空温度,单位为华氏度;Lsun(θi, φi) 为入射方向为
由基尔霍夫定律可知,海水的辐射率ελ和反射率ρλ相加为1,存在
| $ {\varepsilon _\lambda }\left( \chi \right) = 1 - {\rho _\lambda }\left( \chi \right), $ |
式中χ意义与式 (3) 相同.因此可以得到海水反射的辐射亮度为
| $ \begin{array}{l} {L_{\rm{f}}}\left( {\lambda ,{\theta _e},{\varphi _e}} \right) = \\ \;\;\;\;\;\frac{1}{{\cos {\theta _e}}}\int_0^1 {\int_0^{2\pi } {{L_{{\rm{sky}}}}\left( {{\theta _i},{\varphi _i}} \right){\rho _\lambda }\left( \chi \right)\cos \chi u_n^{ - 1}f\left( {{u_n},{\varphi _n}} \right){\rm{d}}{u_n}{\rm{d}}{\varphi _n}} } , \end{array} $ | (6) |
式中un与φn意义与式 (4) 相同.
天空辐射入射方向
| $ \begin{array}{l} {u_n} = \frac{{\sqrt {2 + 2\sin {\theta _i}\sin {\theta _e}\cos \left( {{\varphi _i} - {\varphi _e}} \right) + 2\cos {\theta _i}\cos {\theta _e}} }}{{\cos {\theta _i} + \cos {\theta _e}}},\\ \cos \chi = \frac{{\sqrt {1 + \sin {\theta _i}\sin {\theta _e}\cos \left( {{\varphi _i} - {\varphi _e}} \right) + \cos {\theta _i}\cos {\theta _e}} }}{2}. \end{array} $ |
根据海表面的红外辐射模型和天空反射模型,可以得到红外传感器的温度测量模型,传感器受到的辐射照度可表示为
| $ \begin{gathered} {E_m} = \int_{{\lambda _1}}^{{\lambda _2}} {\iint\limits_\mathit{\Omega } {\left( {{L_{{\rm{sea}}}}\left( {{T_{{\rm{sea}}}},\lambda ,{\theta _e},{\varphi _e}} \right) + } \right.}} \hfill \\ \;\;\;\;\;\;\;\;\;\left. {{L_{\rm{f}}}\left( {\lambda ,{\theta _e},{\varphi _e}} \right)} \right)\cos \beta {\rm{d}}\mathit{\Omega }{\rm{d}}\lambda . \hfill \\ \end{gathered} $ | (7) |
将式 (7) 带入式 (1),即可得到传感器测量温度.式 (7) 对传感器的测量过程进行了建模,在已知真实海表面温度为Tsea、天空温度Tsky、海上风速v及传感器安装的轴线方向
通过实验测量倾斜条件下传感器的测量结果,并与温度测量模型的计算结果进行比较.
实验时天气为多云,测量到的天空温度为12.2 ℃,图 1给出了不同倾斜条件下的海表温度的测量结果.从结果可以看出,模型仿真结果同测量结果基本一致.造成误差的主要原因包括以下几个方面:1) 水表温度不均匀且存在流动,水温存在一定的变化;2) 测量过程中需要人工操作,测量结果可能会受人体红外辐射的影响;3) 传感器倾角存在测量误差.

|
图 1 温度测量模型验证 Figure 1 Verification of measurement model |
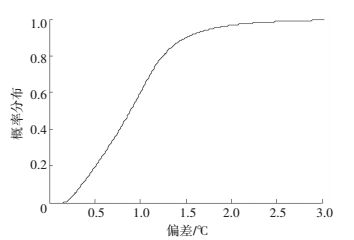
海面辐射率随辐射方向增大而降低,使得传感器测量到的海面辐射亮度降低,同时反射率的增大使得天空温度对测量结果的影响增大.为验证在不同风速、舰船横纵摇条件下,天空红外辐射的影响,仿真了测量偏差的概率分布函数.在一定范围内随机选取风速、纵横摇角度、天空温度及海表温,风速选择范围为0~10 m/s,纵横摇角度选择范围为对应浪级下的倾角范围,天空温度选择范围为-40~20 ℃,海表温选择范围为15~30 ℃.仿真结果见图 2.
|
图 2 测量偏差概率分布 Figure 2 Probability distribution of measurement deviation |
从结果看,若不对海水的辐射率和天空温度的干扰进行修正,测量温度与真实海温间偏差<1.5 ℃的概率<90 %,偏差<1 ℃的概<60%,而偏差<0.3 ℃<6%.
3 海表温度修正算法研究 3.1 海表温度修正算法依据传感器受到的辐射照度Em,以及在
若忽略式 (7) 中的波长,依据史蒂芬-玻尔兹曼定律,可以得到传感器测量温度Tm和真实海温Tsea的关系为
| $ {T_{{\rm{sea}}}} = {\left( {\frac{{T_{\rm{m}}^4 - T_{{\rm{sky}}}^{'4}\left( {1 - \overline {\bar \varepsilon } \left( {{\theta _0},{\varphi _0}} \right)} \right)}}{{\overline {\bar \varepsilon } \left( {{\theta _0},{\varphi _0}} \right)}}} \right)^{1/4}}, $ | (8) |
式中T′sky(θ0, φ0) 和
| $ {{T'}_{{\rm{sky}}}}\left( {{\theta _0},{\varphi _0}} \right) = {\left( {\frac{{\iint\limits_\mathit{\Omega } {{L_{\rm{f}}}\left( {{\theta _e},{\varphi _e}} \right)\cos \beta {\rm{d}}\mathit{\Omega }}}}{{\sigma {{\sin }^2}\alpha \left( {1 - \overline {\bar \varepsilon } \left( {{\theta _0},{\varphi _0}} \right)} \right)}}} \right)^{1/4}}, $ | (9) |
| $ \overline {\bar \varepsilon } \left( {{\theta _0},{\varphi _0}} \right) = \left( {\iint\limits_\mathit{\Omega } {\bar \varepsilon \left( {{\theta _e},{\varphi _e}} \right)\cos \beta {\rm{d}}\mathit{\Omega }}} \right)/\left( {\pi {{\sin }^2}\alpha } \right). $ | (10) |
式中:σ为史蒂芬-玻尔兹曼常数,α、β与Ω与式 (1) 相同,dΩ积分范围为传感器测量的空间角范围,dΩ的方向即为
因此,天空温度修正算法可表述为以下过程:
1) 以舰艏向为y轴建立坐标系,获取舰船纵摇角度α1及横摇角度α2(右手坐标系).
2) 测量海上一定高度上的风速,并计算12.5 m高度上的风速.
3) 获取天空温度Tsky并计算辐射亮度.获取天空温度Tsky的方法包括经验法和测量法,两种方法将通过仿真对比进行选择.
4) 计算传感器轴线方向
| $ \begin{array}{l} \left[ \begin{array}{l} \sin {\theta _0}\cos {\varphi _0}\\ \sin {\theta _0}\sin {\varphi _0}\\ - \cos {\theta _0} \end{array} \right] = \mathit{\boldsymbol{A}}\left( {{\alpha _1}} \right)\mathit{\boldsymbol{A}}\left( {{\alpha _2}} \right)\left[ \begin{array}{l} \sin {\theta _{\rm{s}}}\cos {\varphi _{\rm{s}}}\\ \sin {\theta _{\rm{s}}}\sin {\varphi _{\rm{s}}}\\ - \cos {\theta _{\rm{s}}} \end{array} \right],\\ \mathit{\boldsymbol{A}}\left( {{\alpha _1}} \right) = \left[ {\begin{array}{*{20}{c}} 1 & 0 & 0\\ 0 & {\cos {\alpha _1}} & { - \sin {\alpha _1}}\\ 0 & {\sin {\alpha _1}} & {\cos {\alpha _1}} \end{array}} \right],\\ \mathit{\boldsymbol{A}}\left( {{\alpha _2}} \right) = \left[ {\begin{array}{*{20}{c}} {\cos {\alpha _2}} & 0 & {\sin {\alpha _2}}\\ 0 & 1 & 0\\ { - \sin {\alpha _2}} & 0 & {\cos {\alpha _2}} \end{array}} \right]. \end{array} $ |
传感器测量倾角为45 °时,θs=45 °,安装于左舷的传感器φs=180 °,右舷的传感器φs=0 °.
5) 空间角为dΩ辐射方向为
6) 对空间角为dΩ进行积分,通过式 (9) 和 (10),计算传感器轴线方向
7) 通过式 (8) 计算海水的温度.
3.2 天空温度补偿方法对海表温度进行修正,需要补偿天空的红外辐射温度.天空温度的获取方法包括经验法和测量法.测量法是对天空温度进行测量,需要加装一路对天的传感器,与经验法相比实现过程更为复杂,但补偿精度高;经验法是根据以往的气象条件,选择一个合适天空温度实现修正,实现简单,但补偿精度差.在此,对经验法进行仿真,若此方法的补偿精度可使雷达威力预报结果达到20 %相对误差的指标要求,则可放弃测量法.仿真时使用NPS模型计算蒸发波导折射率廓线[11],PE模型计算电磁波传播损耗[12-13].
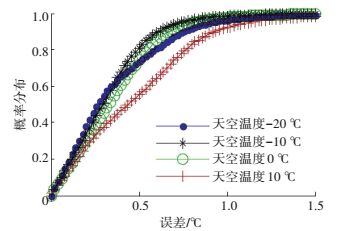
设用于补偿的天空温度分别为20 ℃、-10 ℃、0 ℃和10 ℃,传感器的测量结果使用2.3中的仿真结果. 图 3给出了4种天空温度补偿后仍存在误差的概率分布.从图 3可以看出,选用-10 ℃作为补偿温度误差概率相对较小,小于0.6 ℃的概率为90%,小于0.3 ℃的概率为50 %.
|
图 3 经验法补偿误差的概率分布 Figure 3 Probability distribution of error by empirical method |
若海温误差为0.1 ℃到0.6 ℃,图 4给出了不同温度误差造成的雷达威力预报误差的概率分布函数.气温、海表温、风速及湿度在一定范围内随机选取,其中海温选择范围为15~30 ℃,气海温差选择范围为-2~2 ℃,风速选择范围为0~10 m/s,湿度选择范围为45%~95%.从图 4可以看出,当海温误差为0.1 ℃到0.6 ℃时,预报相对误差小于20 %的概率分别约为96 %、92 %、89 %、86 %、83 %和79 %.因此可以得到,使用经验法得到的修正温度,会导致预报结果相对误差小于20 %概率分别约为71 %.可以看出,采用经验法会使预报误差较大,无法满足雷达威力预报的要求.也有研究指出[14],在稳定层结条件下温度测量误差应小于0.2 ℃,不稳定层结测量误差应小于0.5 ℃.因此在补偿天空温度时应采用测量法.

|
图 4 预报距离误差的概率分布 Figure 4 Probability distribution of detection range error |
为了验证本文方法在实际雷达威力预报中的效果和作用,项目组于2015年8月在江苏北部黄海海域行了为期20 d的海上实验.实验系统由一套水文气象采集器和一台工作于X波段的雷达组成,气象水文采集器用于采集风速、湿度、压强、气温和海温等气象参数,X波段雷达用于探测海上目标,获取雷达可探测到最远目标的距离参数,舰船的倾斜角度通过倾角传感器测得,并将测得的角度和气象数据输送至计算机,计算雷达的探测效能.实验中,共测得有效数据198组,得到雷达威力预报的相对误差分布曲线如图 5所示.

|
图 5 海上实验中预报威力相对误差的概率分布函数 Figure 5 Probability distribution of relative error of predicted detection range |
从图 5可以看出,利用修正的海温实现雷达威力预报,预报结果的误差有显著的降低.使用未修正的海温,预报结果相对误差小于20%的概率约为60%,而使用修正后的海温,预报结果相对误差小于20%的概率大于80%.
预报结果与测试结果仍存在一定的偏差,其原因可能包括以下几个方面:
1) 波导预报模式为单点预报,即假设大气折射率剖面水平均匀分布,仅利用雷达周围的天气参数对整片海域的波导条件进行预报.而在实际探测过程中,大气折射率水平分布均匀的条件不一定成立,尤其是陆地附近,折射率在水平方向上存在较明显的变化[15].
2) 海上目标的RCS不能准确估计.由于被测目标为非合作目标,目标RCS的大小和方向性只能通过人为设置,这在某种程度上造成了测量误差.
3) 舰艇运动过程仍会对采集到的气象水文数据有一定影响,测量结果存在一定的误差.预报模型中,仍存在一些敏感点,使得微小的气象误差会造成较大的预报误差.
5 结语本文针对雷达威力预报系统中的海表面温度的修正方法展开研究.首先研究了红外传感器的测量过程,指出了传感器倾角和天空背景对测量结果的影响.在此基础上对海面红外辐射和天空反射进行建模,给出测量偏差修正公式以及天空温度补偿方法.最后,将提出的海表温度测量及修正方法应用到雷达威力预报中,实验结果表明利用本文方法预报的雷达探测距离相对误差小于20 %的概率高于80 %,具有较高的预报精度.
| [1] | ZHANG Pei, BAI Lu, WU Zhensen, et al. Applying the parabolic equation to tropospheric groundwave propagation[J]. IEEE Antennas & Propagation Magazine, 2016, 58(3): 31-44. DOI: 10.1109/MAP.2016.2541620 |
| [2] |
刘爱国, 察豪, 李忠猛. 岸基微波超视距雷达探测预报方法[J].
华中科技大学学报 (自然科学版), 2014, 42(7): 96-100.
LIU Aiguo, CHA Hao, LI Zhongmeng. Prediction method of coastal microwave OTH radar detection range[J]. Journal Huazhong University of Science & Technology (Natural Science Edition), 2014, 42(7): 96-100. DOI: 10.13245/j.hust.140719 |
| [3] | MESNARD F, SAUVAGEOT H. Climatology of anomalous propagation radar echoes in a coastal area[J]. Journal of Applied Meteorology & Climatology, 2010, 49(11): 2285-2300. DOI: 10.1175/2010JAMC2440.1 |
| [4] | APAYDIN G, SEVGI L. MatLab-based FEM-parabolic equation tool for path loss calculations along multi-mixed-terrain paths[J]. IEEE Antennas & Propagation Magazine, 2014, 56(3): 221-236. DOI: 10.1109/MAP.2014.6867720 |
| [5] | ANDERSON K, BROOKS B, CAFFREY P, et al. TheRED experiment: an assessment of boundary layer effects in a trade winds regime on microwave and infrared propagation over the sea[J]. Bulletin of The American Meteorological Society, 2004, 85(9): 1355-1365. DOI: 10.1175/BAMS-85-9-1355 |
| [6] | LI H, PINEL N, BOURLIER C. Polarized infrared reflectivity of 2D sea surfaces with two surface reflections[J]. Remote Sensing of Environment, 2014, 147(9): 145-155. DOI: 10.1016/j.rse.2014.02.018 |
| [7] |
谷延锋, 丰炳波, 郑贺, 等. 基于多时相多光谱红外图像浅层地下目标探测[J].
哈尔滨工业大学学报, 2016, 48(3): 1-10.
GU Yanfeng, FENG Bingbo, ZHENG He, et al. Detection of subsurface targets based on multitemporal and multispectral infrared image[J]. Journal of Harbin Institute of Technology, 2016, 48(3): 1-10. DOI: 10.11918/hitxb20140303 |
| [8] |
杨尧, 吴振森, 姚连兴, 等. 从红外辐照热平衡方程求解海面温度[J].
红外与毫米波学报, 2003, 22(5): 357-360.
YANG Yao, WU Zhensen, YAO Lianxing, et al. Solving the sea surface temperature from the infrared radiation heat balance equation[J]. Journal Infrared Millimeter Waves, 2003, 22(5): 357-360. DOI: 10.3321/j.issn:1001-9014.2003.05.009 |
| [9] |
易金桥, 黄勇, 廖红华, 等. 热释电红外传感器及其在人员计数系统中的应用[J].
红外与激光工程, 2015, 44(4): 1186-1192.
YI Jinqiao, HUANG Yong, LIAO Honghua, et al. Pyro electric infrared sensor and its application in people counting system[J]. Infrared and Laser Engineering, 2015, 44(4): 1186-1192. DOI: 10.3969/j.issn.1007-2276.2015.04.014 |
| [10] | KARINE C, SANDRINE F, CHRISTOPHE B. Multiresolution optical characteristics of rough sea surface in the infrared[J]. Applied Optics, 2007, 22(46): 5471-5481. DOI: 10.1364/AO.46.005471 |
| [11] | ZHANG Jinpeng, WU Zensen, ZHU Qinglin, et al. A four parameter M-profile model for the evaporation duct estimation from radar clutter[J]. Progress in Electromagnetics Research, 2011, 114(8): 353-368. DOI: 10.2528/PIER11012204 |
| [12] | SIRKOVA I, MIKHAVLEV M. Parabolic wave equation method applied to the tropospheric ducting propagation problem: a survey[J]. Electromagnetics, 2006, 26(2): 155-173. DOI: 10.1080/02726340500486484 |
| [13] | SHENG Zheng. The estimation of lower refractivity uncertainty from radar sea clutter using the Bayesian-MCMC method[J]. Chinese Physics B, 2013(22): 580-585. DOI: 10.1088/1674-1056/22/2/029302 |
| [14] | GRACHEV A A, ANDREAS E L, FAIRALL C W, et al. SHEBA flux-profile relationships in the stable atmospheric boundary layer[J]. Boundary-Layer Meteorology, 2007, 124(3): 315-333. DOI: 10.1007/s10546-007-9177-6 |
| [15] | ZHANG Qi, YANG Kunde, SHI Yang. Spatial and temporal variability of the evaporation duct in the Gulf of Aden[J]. Tellus, 2016, 68: 1-14. DOI: 10.3402/tellusa.v68.29792. |
 2017, Vol. 49
2017, Vol. 49


