波达方向 (direction-of-arrival, DOA) 估计在雷达、声呐、无线通信等众多应用领域有着重要作用[1-2]. Schmidt等[3]提出的多重信号分类 (multiple signal classification, MUSIC) 是最具有代表性的DOA估计方法,是一种基于信源协方差矩阵特征分解的子空间类方法,具有较高的分辨率.
随着科技的快速发展,对DOA估计的分辨率也提出更高的要求.虚拟天线阵是一种研究构造虚拟阵元的方法和将实际天线阵转换为虚拟天线阵的先进技术,主要包括内插变换法[4-5]和四阶量法[6-8].将虚拟天线阵技术与MUSIC方法结合,可以增加天线阵的自由度,有效提高天线阵DOA估计的分辨率.内插变换法通过在实际阵元间插入虚拟阵元,提高了MUSIC方法的分辨率[5],但是内插变换法不利于阵列孔径扩展,对分辨率的提高有限.基于四阶量的MUSIC (fourth-order MUSIC, FOMUSIC) 方法能够有效地扩展阵列孔径,并提高阵列的分辨率[6],是一种高分辨率的DOA估计方法.
FOMUSIC方法能够扩展阵列孔径,但是运算量较大[9]. Akkar等[10]利用正交分解代替特征分解;Lie等[11]用二阶和四阶协方差矩阵进行混合估计;Wang等[12]则去除了四阶量矩阵中的部分冗余信息,都减小了FOMUSIC方法的运算量. Liao等[13]利用基于行列式的空间谱,实现了未知互耦情况下的DOA估计;宋海岩等[14]用一组四阶量矩阵进行联合对角化,能处理相干信号,且与单个四阶量矩阵相比获得了更高的分辨率;Li[15]等通过增强信号子空间,减小了内插变换法的变换误差,与常规内插变换法相比分辨率更高,且运算量较小;Shan等[16]提出了共轭扩展多重信号分类 (conjugate augmented MUSIC, CAM) 方法,通过扩展阵列导向矢量以及协方差矩阵所含信息,大幅提高了分辨率,是一种分辨率极高的虚拟天线阵DOA估计方法.
为了进一步提高天线阵DOA估计的分辨率,本文提出一种基于二次虚拟扩展的多重信号分类 (twice virtual expansion MUSIC, TVEM) 方法.该方法先求出阵列接收数据的四阶矩量,以及相应扩展的阵列导向矢量,再求出阵列接收数据及其共轭,以及相应扩展的阵列导向矢量,实现二次虚拟扩展,构造了更多的虚拟阵元,进一步提高了天线阵DOA估计的分辨率.
1 天线阵模型及MUSIC方法考虑远场情况下的非相干窄带信号,天线为N元均匀直线阵,阵元间距d为半波长λ/2,天线阵接收数据矩阵表示为
| $ \mathit{\boldsymbol{X}}\left( t \right) = {\left[ {{x_1}\left( t \right), \cdots ,{x_N}\left( t \right)} \right]^{\rm{T}}} = \mathit{\boldsymbol{AS}}\left( t \right) + \mathit{\boldsymbol{N}}\left( t \right). $ | (1) |
式中:M为信源数,(·)T表示转置,A=[a1(θ), a2(θ), …, aM(θ)]为阵列导向矢量矩阵,S(t) 为信号复包络,N(t) 为天线阵的噪声.
阵列接收数据的协方差矩阵为
| $ \begin{array}{l} {\mathit{\boldsymbol{R}}_{{\rm{xx}}}} = {\rm{E}}\left\{ {\mathit{\boldsymbol{X}}\left( t \right){\mathit{\boldsymbol{X}}^{\rm{H}}}\left( t \right)} \right\} = \mathit{\boldsymbol{A}}{\rm{E}}\left\{ {\mathit{\boldsymbol{S}}\left( t \right){\mathit{\boldsymbol{S}}^{\rm{H}}}\left( t \right)} \right\}{\mathit{\boldsymbol{A}}^{\rm{H}}} + \\ \;\;\;\;\;\;\;\;\;{\rm{E}}\left\{ {\mathit{\boldsymbol{N}}\left( t \right){\mathit{\boldsymbol{N}}^{\rm{H}}}\left( t \right)} \right\} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{R}}_{{\rm{SS}}}}{\mathit{\boldsymbol{A}}^{\rm{H}}} + \delta _{\rm{n}}^2\mathit{\boldsymbol{I}}. \end{array} $ |
本文设信号与噪声相互独立,因此阵列接收数据的协方差矩阵可分解为信号和噪声两部分. RSS为信号协方差矩阵,δn2I为噪声协方差矩阵,E{·}表示数学期望,(·)H表示共轭转置,I表示单位矩阵.
协方差矩阵Rxx是Hermitian矩阵,特征分解后为
| $ {\mathit{\boldsymbol{R}}_{{\rm{xx}}}} = \mathit{\boldsymbol{U \boldsymbol{\varSigma} }}{\mathit{\boldsymbol{U}}^{\rm{H}}}, $ |
式中Σ=diag[λ1, …, λN]是Rxx的特征值按降序排列组成的对角阵,U为特征向量矩阵.
将Rxx的特征向量根据特征值的大小分为信号和噪声两个部分:
| $ {\mathit{\boldsymbol{R}}_{{\rm{xx}}}} = {\mathit{\boldsymbol{U}}_{\rm{S}}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{\rm{S}}}\mathit{\boldsymbol{U}}_{\rm{S}}^{\rm{H}} + {\mathit{\boldsymbol{U}}_{\rm{N}}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{\rm{N}}}\mathit{\boldsymbol{U}}_{\rm{N}}^{\rm{H}}, $ |
式中US为大特征值所对应的信号子空间,UN为小特征值所对应的噪声子空间.
根据协方差矩阵信号子空间与噪声子空间的正交性,可以由噪声子空间估计出信号的波达方向,在实际计算中,Rxx通常用有限次快拍数K的采样协方差矩阵代替:
| $ {{\mathit{\boldsymbol{\hat R}}}_{{\rm{xx}}}} = \frac{1}{K}\sum\limits_{k = 1}^K {\mathit{\boldsymbol{X}}\left( k \right){\mathit{\boldsymbol{X}}^{\rm{H}}}\left( k \right)} . $ |
MUSIC算法的空间谱为
| $ {P_{{\rm{MUSIC}}}} = \frac{1}{{{\mathit{\boldsymbol{a}}^{\rm{H}}}\left( \theta \right){\mathit{\boldsymbol{U}}_{\rm{N}}}\mathit{\boldsymbol{U}}_{\rm{N}}^{\rm{H}}\mathit{\boldsymbol{a}}\left( \theta \right)}}, $ |
式中a(θ) 为阵列导向矢量.再通过对PMUSIC谱峰搜索即可估计出信号的波达方向. MUSIC方法是一种分辨率较高的DOA估计方法,但是当信源数超过实际阵元数时,MUSIC方法将会失效,此外,MUSIC方法的分辨率也受到实际阵列孔径的限制.
2 FOMUSIC方法用四阶量替代二阶量进行DOA估计,可以保留更丰富的波达方向信息,获得更好的DOA估计性能[7].设x(t) 为零均值平稳实随机过程,则其四阶累积量矩阵为
| $ \begin{array}{l} {\rm{cum}}\left( {{\mathit{\boldsymbol{x}}_{{{\rm{k}}_1}}},\mathit{\boldsymbol{x}}_{{{\rm{k}}_2}}^ * ,\mathit{\boldsymbol{x}}_{{{\rm{k}}_3}}^ * ,{\mathit{\boldsymbol{x}}_{{{\rm{k}}_4}}}} \right) = \\ \;\;\;\;{\rm{E}}\left\{ {{\mathit{\boldsymbol{x}}_{{{\rm{k}}_1}}}\left( t \right)\mathit{\boldsymbol{x}}_{{{\rm{k}}_2}}^ * \left( t \right)\mathit{\boldsymbol{x}}_{{{\rm{k}}_3}}^ * \left( t \right){\mathit{\boldsymbol{x}}_{{{\rm{k}}_4}}}\left( t \right)} \right\} - \\ \;\;\;\;{\rm{E}}\left\{ {{\mathit{\boldsymbol{x}}_{{{\rm{k}}_1}}}\left( t \right)\mathit{\boldsymbol{x}}_{{{\rm{k}}_2}}^ * \left( t \right)} \right\}{\rm{E}}\left\{ {\mathit{\boldsymbol{x}}_{{{\rm{k}}_3}}^ * \left( t \right){\mathit{\boldsymbol{x}}_{{{\rm{k}}_4}}}\left( t \right)} \right\} - \\ \;\;\;\;{\rm{E}}\left\{ {{\mathit{\boldsymbol{x}}_{{{\rm{k}}_1}}}\left( t \right)\mathit{\boldsymbol{x}}_{{{\rm{k}}_3}}^ * \left( t \right)} \right\}{\rm{E}}\left\{ {\mathit{\boldsymbol{x}}_{{{\rm{k}}_2}}^ * \left( t \right){\mathit{\boldsymbol{x}}_{{{\rm{k}}_4}}}\left( t \right)} \right\}, \end{array} $ | (2) |
式中 (·)*表示共轭.式 (2) 可以表示为[7]
| $ \begin{array}{l} {\mathit{\boldsymbol{C}}_{4{\rm{x}}}} = {\rm{E}}\left\{ {\left[ {\mathit{\boldsymbol{X}}\left( t \right) \otimes {\mathit{\boldsymbol{X}}^ * }\left( t \right)} \right]{{\left[ {\mathit{\boldsymbol{X}}\left( t \right) \otimes {\mathit{\boldsymbol{X}}^ * }\left( t \right)} \right]}^{\rm{H}}}} \right\} - \\ \;\;\;\;\;\;\;\;\;{\rm{E}}\left\{ {\mathit{\boldsymbol{X}}\left( t \right) \otimes {\mathit{\boldsymbol{X}}^ * }\left( t \right)} \right\}{\rm{E}}\left\{ {{{\left[ {\mathit{\boldsymbol{X}}\left( t \right) \otimes {\mathit{\boldsymbol{X}}^ * }\left( t \right)} \right]}^{\rm{H}}}} \right\} - \\ \;\;\;\;\;\;\;\;\;{\rm{E}}\left\{ {\mathit{\boldsymbol{X}}\left( t \right){\mathit{\boldsymbol{X}}^{\rm{H}}}\left( t \right)} \right\} \otimes {\rm{E}}\left\{ {{{\left[ {\mathit{\boldsymbol{X}}\left( t \right){\mathit{\boldsymbol{X}}^{\rm{H}}}\left( t \right)} \right]}^ * }} \right\}. \end{array} $ | (3) |
式中
| $ {\mathit{\boldsymbol{D}}_{4{\rm{x}}}} = {\rm{E}}\left\{ {\left[ {\mathit{\boldsymbol{X}}\left( t \right) \otimes {\mathit{\boldsymbol{X}}^ * }\left( t \right)} \right]{{\left[ {\mathit{\boldsymbol{X}}\left( t \right) \otimes {\mathit{\boldsymbol{X}}^ * }\left( t \right)} \right]}^{\rm{H}}}} \right\}. $ |
式中:X(t) 为N×K维矩阵,X(t)
根据克罗内克积的性质[17],将式 (1) 代入X(t)
| $ \begin{array}{l} \mathit{\boldsymbol{X}}\left( t \right) \otimes {\mathit{\boldsymbol{X}}^*}\left( t \right) = \left[ {\mathit{\boldsymbol{AS}}\left( t \right) + \mathit{\boldsymbol{N}}\left( t \right)} \right] \otimes \\ \;\;\;\;\;\;{\left[ {\mathit{\boldsymbol{AS}}\left( t \right) + \mathit{\boldsymbol{N}}\left( t \right)} \right]^*} = \left[ {\mathit{\boldsymbol{AS}}\left( t \right)} \right] \otimes \\ \;\;\;\;\;\;{\left[ {\mathit{\boldsymbol{AS}}\left( t \right)} \right]^*} + \mathit{\boldsymbol{N}}\left( t \right) \otimes {\mathit{\boldsymbol{N}}^*}\left( t \right) = \\ \;\;\;\;\;\;\left( {\mathit{\boldsymbol{A}} \otimes {\mathit{\boldsymbol{A}}^*}} \right)\left[ {\mathit{\boldsymbol{S}}\left( t \right) \otimes {\mathit{\boldsymbol{S}}^*}\left( t \right)} \right] + \\ \;\;\;\;\;\;\;\mathit{\boldsymbol{N}}\left( t \right) \otimes {\mathit{\boldsymbol{N}}^*}\left( t \right). \end{array} $ | (4) |
再将式 (4) 代入D4x[7]:
| $ \begin{array}{l} {\mathit{\boldsymbol{D}}_{4x}} = {\rm{E}}\left\{ {\left[ {\mathit{\boldsymbol{X}}\left( t \right) \otimes {\mathit{\boldsymbol{X}}^ * }\left( t \right)} \right]{{\left[ {\mathit{\boldsymbol{X}}\left( t \right) \otimes {\mathit{\boldsymbol{X}}^ * }\left( t \right)} \right]}^{\rm{H}}}} \right\} = \\ \;\;\;\;\;\;\;\;\;\;\left( {\mathit{\boldsymbol{A}} \otimes {\mathit{\boldsymbol{A}}^ * }} \right){\rm{E}}\left\{ {\left[ {\mathit{\boldsymbol{S}}\left( t \right) \otimes {\mathit{\boldsymbol{S}}^ * }\left( t \right)} \right] \cdot } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {{{\left[ {\mathit{\boldsymbol{S}}\left( t \right) \otimes {\mathit{\boldsymbol{S}}^ * }\left( t \right)} \right]}^{\rm{H}}}} \right\}{\left( {\mathit{\boldsymbol{A}} \otimes {\mathit{\boldsymbol{A}}^ * }} \right)^{\rm{H}}} + \\ \;\;\;\;\;\;\;\;\;\;{\rm{E}}\left\{ {\left[ {\mathit{\boldsymbol{N}}\left( t \right) \otimes {\mathit{\boldsymbol{N}}^ * }\left( t \right)} \right]{{\left[ {\mathit{\boldsymbol{N}}\left( t \right) \otimes {\mathit{\boldsymbol{N}}^ * }\left( t \right)} \right]}^{\rm{H}}}} \right\} = \\ \;\;\;\;\;\;\;\;\;\;\left( {\mathit{\boldsymbol{A}} \otimes {\mathit{\boldsymbol{A}}^ * }} \right){\mathit{\boldsymbol{D}}_{4{\rm{S}}}}{\left( {\mathit{\boldsymbol{A}} \otimes {\mathit{\boldsymbol{A}}^ * }} \right)^{\rm{H}}} + {\mathit{\boldsymbol{D}}_{4{\rm{N}}}}. \end{array} $ | (5) |
式中:A
与推导四阶矩量矩阵的式 (5) 类似,可由式 (3) 推导出四阶累积量矩阵为
| $ {\mathit{\boldsymbol{C}}_{4x}} = \left( {\mathit{\boldsymbol{A}} \otimes {\mathit{\boldsymbol{A}}^ * }} \right){\mathit{\boldsymbol{C}}_{4{\rm{S}}}}{\left( {\mathit{\boldsymbol{A}} \otimes {\mathit{\boldsymbol{A}}^ * }} \right)^{\rm{H}}} + {\mathit{\boldsymbol{C}}_{4{\rm{N}}}}, $ | (6) |
式中C4S和C4N分别为信号和噪声的四阶累积量矩阵.由式 (5) 和式 (6) 可知,与二阶协方差矩阵相比,四阶协方差矩阵的维度得到了扩展,所含波达方向信息也更丰富,实际阵列通过克罗内克积运算被转换为虚拟阵列,阵列孔径得到了扩展.
由式 (3) 得到C4x,再对其特征分解得到噪声子空间U4N,根据噪声子空间与信号子空间的正交性,可知,FOMUSIC方法的空间谱为
| $ {P_{{\rm{FOMUSIC}}}} = \frac{1}{{\mathit{\boldsymbol{b}}{{\left( \theta \right)}^{\rm{H}}}{\mathit{U}_{4{\rm{N}}}}\mathit{\boldsymbol{U}}_{4{\rm{N}}}^{\rm{H}}\mathit{\boldsymbol{b}}\left( \theta \right)}}, $ |
式中b(θ)=a(θ)⊗a*(θ) 为扩展后的阵列导向矢量.
FOMUSIC方法将实际阵列转换为虚拟阵列,扩展了阵列孔径,能够在信源数超过实际阵元数的情况下进行DOA估计,与MUSIC方法相比,分辨率也更高.
3 TVEM方法为了进一步提高天线阵DOA估计的分辨率,本文在FOMUSIC方法的基础上,提出了TVEM方法,该方法通过二次虚拟扩展,构造了更多的虚拟阵元,能够获得比FOMUSIC方法更高的分辨率.
先求出阵列接收数据的四阶矩量,进行第一次虚拟扩展,阵列接收数据X(t) 的四阶矩量为
| $ \mathit{\boldsymbol{X}}{u_1}\left( t \right) = \mathit{\boldsymbol{X}}\left( t \right) \otimes {\mathit{\boldsymbol{X}}^ * }\left( t \right). $ | (7) |
根据克罗内克积的性质[17],将式 (1) 代入式 (7) 得
| $ \begin{array}{l} \mathit{\boldsymbol{X}}{u_1}\left( t \right) = \mathit{\boldsymbol{X}}\left( t \right) \otimes {\mathit{\boldsymbol{X}}^ * }\left( t \right) = \left[ {\mathit{\boldsymbol{AS}}\left( t \right) + \mathit{\boldsymbol{N}}\left( t \right)} \right] \otimes \\ \;\;\;\;\;{\left[ {\mathit{\boldsymbol{AS}}\left( t \right) + \mathit{\boldsymbol{N}}\left( t \right)} \right]^ * } = \left[ {\mathit{\boldsymbol{AS}}\left( t \right)} \right] \otimes {\left[ {\mathit{\boldsymbol{AS}}\left( t \right)} \right]^ * } + \\ \;\;\;\;\;\mathit{\boldsymbol{N}}\left( t \right) \otimes {\mathit{\boldsymbol{N}}^ * }\left( t \right) = \left( {\mathit{\boldsymbol{A}} \otimes {\mathit{\boldsymbol{A}}^ * }} \right)\left[ {\mathit{\boldsymbol{S}}\left( t \right) \otimes {\mathit{\boldsymbol{S}}^ * }\left( t \right)} \right] + \\ \;\;\;\;\;\mathit{\boldsymbol{N}}\left( t \right) \otimes {\mathit{\boldsymbol{N}}^ * }\left( t \right), \end{array} $ |
式中Xu1为N2×K维矩阵,A⊗A*为扩展后的阵列导向矢量矩阵.扩展后的阵列导向矢量为
| $ \begin{array}{l} \mathit{\boldsymbol{b}}\left( \theta \right) = \mathit{\boldsymbol{a}}\left( \theta \right) \otimes {\mathit{\boldsymbol{a}}^ * }\left( \theta \right) = {\left[ {1,{{\rm{e}}^{ - {\rm{j}}\frac{{2\pi d}}{\lambda }\sin \theta }}, \cdots ,{{\rm{e}}^{ - {\rm{j}}\frac{{2\pi \left( {N - 1} \right)d}}{\lambda }\sin \theta }}} \right]^{\rm{T}}} \otimes \\ {\left[ {1,{{\rm{e}}^{ - {\rm{j}}\frac{{2\pi d}}{\lambda }\sin \theta }}, \cdots ,{{\rm{e}}^{ - {\rm{j}}\frac{{2\pi \left( {N - 1} \right)d}}{\lambda }\sin \theta }}} \right]^{\rm{H}}} = \\ {\left[ {1,{{\rm{e}}^{ - {\rm{j}}\frac{{2\pi d}}{\lambda }\sin \theta }}, \cdots ,{{\rm{e}}^{ - {\rm{j}}\frac{{2\pi \left( {N - 1} \right)d}}{\lambda }\sin \theta }},{{\rm{e}}^{ - {\rm{j}}\frac{{2\pi d}}{\lambda }\sin \theta }}, \cdots ,{{\rm{e}}^{ - {\rm{j}}\frac{{2\pi \left( {2N - 2} \right)d}}{\lambda }\sin \theta }}} \right]^{\rm{T}}}. \end{array} $ | (8) |
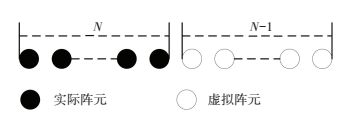
由式 (8) 可知,b(θ) 中有大量冗余,只有2N-1个非重复元素,即第一次虚拟阵列扩展的阵元位置,如图 1所示.
|
图 1 第一次虚拟扩展的虚拟阵元位置 Figure 1 Position diagram of virtual array elements of the first extension |
再求出阵列接收数据及其共轭,进行第二次虚拟扩展.假设X(t) 是X(t) 以行为单位上下翻转得到的数据,a(θ) 是a(θ) 上下翻转得到的导向矢量,求出阵列接收数据X(t) 及其共轭:
| $ \mathit{\boldsymbol{X}}{\mathit{u}_2}\left( t \right) = \left[ \begin{array}{l} {{\mathit{\boldsymbol{\bar X}}}^ * }\left( t \right)\\ \mathit{\boldsymbol{X}}\left( t \right) \end{array} \right]. $ |
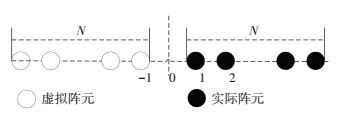
以第一个实际阵元左侧d处为参考点,则扩展后的阵列导向矢量为b(θ)=
|
图 2 第二次虚拟扩展的虚拟阵元位置 Figure 2 Position diagram of virtual array elements of the second extension |
求出二次虚拟扩展后的扩展协方差矩阵:
| $ {\mathit{\boldsymbol{R}}_{{\rm{Xu}}}} = \frac{1}{K}\left[ \begin{array}{l} \mathit{\boldsymbol{X}}{\mathit{u}_2}\left( t \right)\\ \mathit{\boldsymbol{X}}{\mathit{u}_1}\left( t \right) \end{array} \right] \cdot {\left[ \begin{array}{l} \mathit{\boldsymbol{X}}{\mathit{u}_2}\left( t \right)\\ \mathit{\boldsymbol{X}}{\mathit{u}_1}\left( t \right) \end{array} \right]^{\rm{H}}}. $ | (9) |
对Ru进行特征分解:
| $ {\mathit{\boldsymbol{R}}_u} = {\mathit{\boldsymbol{U}}_{{\rm{uS}}}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{{\rm{uS}}}}\mathit{\boldsymbol{U}}_{{\rm{uS}}}^{\rm{H}} + {\mathit{\boldsymbol{U}}_{{\rm{uN}}}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{{\rm{uN}}}}\mathit{\boldsymbol{U}}_{{\rm{uN}}}^{\rm{H}}, $ |
式中UuN为噪声子空间.
二次虚拟扩展后的虚拟阵列导向矢量为
| $ \mathit{\boldsymbol{c}}\left( \theta \right) = \left[ \begin{array}{l} \mathit{\boldsymbol{\bar b}}\left( \theta \right)\\ \mathit{\boldsymbol{b}}\left( \theta \right) \end{array} \right]. $ | (10) |
由式 (10) 和图 1、图 2可知,通过二次虚拟扩展,实际阵列被转换为虚拟阵列,阵列的导向矢量得到了进一步的扩展,构造了更多的虚拟阵元. TVEM方法的空间谱为
| $ {P_{{\rm{TVEM}}}} = \frac{1}{{\mathit{\boldsymbol{c}}{{\left( \theta \right)}^{\rm{H}}}{\mathit{\boldsymbol{U}}_{{\rm{uN}}}}\mathit{\boldsymbol{U}}_{{\rm{uN}}}^{\rm{H}}\mathit{\boldsymbol{c}}\left( \theta \right)}}. $ |
TVEM方法先求出阵列接收数据的四阶矩量,以及相应扩展的阵列导向矢量,再求出阵列接收数据及其共轭,以及相应扩展的阵列导向矢量,通过二次虚拟扩展,将实际阵列转换为虚拟阵列. TVEM方法分辨率提高的原因可以从数学和物理意义两方面进行分析:从数学上看,如式 (6)、(9) 所示,TVEM方法中协方差矩阵得到扩展,其中包含了更多的波达方向信息和冗余,从而提高了分辨率;从物理意义上看,如图 1、2所示,TVEM方法构造了更多的虚拟阵元,扩展了阵列孔径,因此获得了比FOMUSIC方法更高的分辨率.
4 运算量分析将常规MUSIC方法、FOMUSIC方法、CAM方法[16]以及本文提出的TVEM方法的计算复杂度进行比较,如表 1所示.
| 表 1 4种方法计算复杂度对比 Table 1 Computational complexity of the four methods |
由表 1可知,在未去冗余的情况下,FOMUSIC法、CAM法和TVEM法这3种基于四阶量的虚拟天线阵DOA估计方法的计算复杂度远高于MUSIC法,这是因为四阶量矩阵中包含大量冗余,其中CAM法计算复杂度比TVEM法高,TVEM法计算复杂度比FOMUSIC法高.在天线阵为均匀直线阵的情况下,能够去除四阶量矩阵中的冗余[16],此时TVEM法的计算复杂度与CAM方法十分接近,而TVEM法的计算复杂度明显高于FOMUSIC法,这是因为TVEM法通过二次虚拟扩展,构造了比FOMUSIC法更多的虚拟阵元,从而获得了更高的分辨率,其代价是运算量增大.
5 仿真分析考虑远场窄带情况下的来波信号,信号之间互不相关,天线阵为四元均匀直线阵,阵元间距为半波长,快拍数为200.下面通过三组仿真实验,比较TVEM方法、FOMUSIC方法和CAM方法[16]的分辨率,三组仿真结果均通过200次重复独立实验得到.分辨率的评价指标采用均方误差和成功概率.成功概率的计算方法为:独立重复实验中,波达方向估计的误差低于门限值的次数与总次数之比,仿真中门限值设为0.2°.
5.1 在信源数少于实际阵元数的情况下,比较3种方法的分辨率仿真1 信源数为3,来波方向为-45°、0°和40°,其中天线阵法线方向设为0°,左侧为-90°到0,右侧为0°到90°.
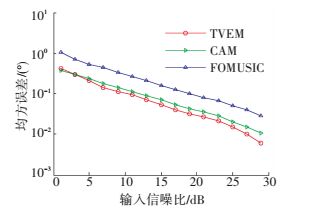
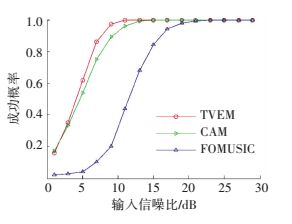
图 3为3种方法的均方误差 (root mean square error, RMSE) 随输入信噪比RSN的变化曲线,其中RSN表示天线阵输入的期望信号功率与噪声功率之比;图 4为3种方法的成功概率随输入信噪比的变化曲线.
|
图 3 输入信噪比变化时3种方法的均方误差曲线 Figure 3 RMSE versus RSN of the three methods |
|
图 4 输入信噪比变化时3种方法的成功概率曲线 Figure 4 Probability of target resolution versus RSN of the three methods |
从图 3可以看出:当RSN低于3 dB时,TVEM法的均方误差高于CAM法,当RSN高于3 dB时,TVEM法的均方误差低于CAM法;总体上,TVEM法的均方误差略低于CAM方法,且二者的均方误差都明显低于FOMUSIC法.从图 4可以看出:当RSN低于3 dB时,TVEM法的成功概率低于CAM法,当RSN高于3 dB时,TVEM法的成功概率高于CAM法;总体上,TVEM法的成功概率略高于CAM法,且二者的成功概率都明显高于FOMUSIC法.由此可知,在信源数少于实际阵元数的情况下,TVEM法的分辨率略高于CAM法,明显高于FOMUSIC法.
5.2 在波达角度较为接近的情况下,比较3种方法的分辨率仿真2 信源数为2,来波方向为-3°和3°.
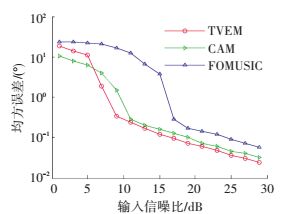
图 5为3种方法的均方误差随输入信噪比的变化曲线. 图 6为3种方法的成功概率随输入信噪比的变化曲线.
|
图 5 输入信噪比变化时3种方法的均方误差曲线 Figure 5 RMSE versus RSN of the three methods |
|
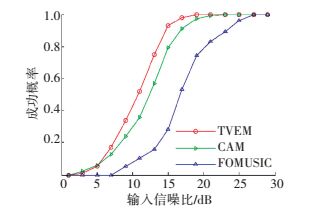
图 6 输入信噪比变化时3种方法的成功概率曲线 Figure 6 Probability of target resolution versus RSN of the three methods |
从图 5可以看出, 在波达角度较为接近的情况下,随着RSN不断提高,3种DOA估计方法的均方误差都不断下降,3种方法均方误差曲线的变化过程都可以大致分为3个阶段.第一阶段,RSN相对较低时,均方误差较大且下降较为缓慢;第二阶段,随着RSN的提高,均方误差快速下降;第三阶段,RSN提高到一定值后,均方误差相对较小且平稳下降.这是因为当RSN较低时,DOA估计方法无法分辨波达角度较为接近的信源,因而均方误差很大且下降较为缓慢;随着RSN不断提高,DOA估计方法可以在一定程度上分辨波达角度较为接近的信源,此时均方误差快速下降;当RSN达到一定值后,DOA估计方法可以相对有效地分辨波达角度较为接近的信源,则均方误差相对较小且平稳下降.对比图 5中3种方法的均方误差曲线可以知道,TVEM法的均方误差曲线在RSN超过9 dB后进入第三阶段,CAM法的均方误差曲线在RSN超过11 dB后进入第三阶段,FOMUSIC法的均方误差曲线在RSN超过17 dB后进入第三阶段.此外,在第二、三阶段,TVEM法的均方误差略低于CAM法,明显低于FOMUSIC法.由此可知,TVEM法的均方误差略低于CAM法,明显低于FOMUSIC法.
从图 6可以看出:当RSN低于5 dB时,TVEM法的成功概率略低于CAM法,当RSN高于5 dB时,TVEM法的成功概率高于CAM法;总体上,TVEM法的成功概率略高于CAM法,且二者的成功概率都明显高于FOMUSIC法.由图 5和图 6可知,在波达角度较为接近的情况下,TVEM法的分辨率略高于CAM法,明显高于FO-MUSIC法.
5.3 在信源数超过实际阵元数的情况下,比较3种方法的分辨率仿真3 信源数为5,来波方向为-50°、-25°、0°、15°和45°.
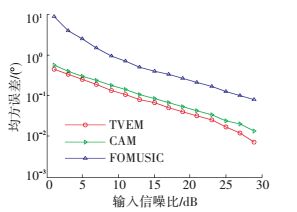
图 7为3种方法的均方误差随输入信噪比的变化曲线,图 8为3种方法的成功概率随输入信噪比的变化曲线.
|
图 7 输入信噪比变化时3种方法的均方误差曲线 Figure 7 RMSE versus RSN of the three methods |
|
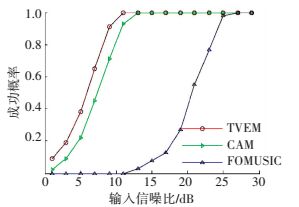
图 8 输入信噪比变化时3种方法的成功概率曲线 Figure 8 Probability of target resolution versus RSN of the three methods |
从图 7可以看出,TVEM法的均方误差低于CAM法,CAM法的均方误差低于FOMUSIC法.从图 8可以看出,TVEM法的成功概率高于CAM法,CAM法的成功概率高于FOMUSIC法.由此可知,在信源数超过实际阵元数的情况下,TVEM法的分辨率略高于CAM法,明显高于FOMUSIC法.
由上述仿真结果可知,TVEM方法的分辨率略高于CAM方法,且TVEM方法的分辨率明显高于FOMUSIC方法.因此,TVEM方法是进一步提高天线阵DOA估计分辨率的一种有效方法.
6 结论本文提出的基于二次虚拟扩展的高分辨率波达方向估计方法,通过阵列接收数据的四阶矩量和共轭,扩展了阵列的导向矢量和协方差矩阵,构造出更多的虚拟阵元,并扩展了阵列的孔径.将实际天线阵转换为虚拟天线阵,实现了二次虚拟扩展,进一步提高了天线阵DOA估计的分辨率.仿真结果表明,本文所提出的方法与四阶量多重信号分类等DOA估计方法相比,具有更低的均方误差和更高的成功概率,是一种提高天线阵DOA估计分辨率的有效方法.
| [1] | WANG Yi, YANG Minglei, CHEN Baixiao, et al. Improved DOA estimation based on real-valued array covariance using sparse Bayesian learning[J]. Signal Processing, 2016, 129(C): 183-189. DOI: 10.1016/j.sigpro.2016.06.002 |
| [2] |
闫锋刚, 张薇, 金铭. 求根MUSIC初值设置和更新算法[J].
哈尔滨工业大学学报, 2015, 47(3): 88-92.
YAN Fenggang, ZHANG Wei, JIN Ming. A new method for setting and updating theinitiation of root-MUSIC[J]. Journal of Harbin Institute of Technology, 2015, 47(3): 88-92. DOI: 10.11918/j.issn.0367-6234.2015.03.015 |
| [3] | SCHMIDT R O. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276-280. DOI: 10.1109/TAP.1986.1143830 |
| [4] | BELLONI F, RICHTER A, KOIVUNEN V. DOA estimation via manifold separation for arbitrary array structures[J]. IEEE Transactions on Signal Processing, 2007, 55(10): 4800-4810. DOI: 10.1109/TSP.2007.896115 |
| [5] | WANG Yongliang, CHEN Hui, WAN Shanhu. An effective DOA method via virtual array transformation[J]. Science in China Series E, 2001, 44(1): 75-82. DOI: 10.1007/BF02916727 |
| [6] | LI Xiukun, LI Tingting, GU Xinyu, et al. Array gain of fourth-order cumulants beamforming under typical probability denisity background[J]. Chinese Journal of Acoustics, 2015, 34(1): 15-26. DOI: 10.15949/j.cnki.0217-9776.2015.01.002 |
| [7] |
丁齐, 魏平, 肖先赐. 基于四阶累积量的DOA估计方法及其分析[J].
电子学报, 1999, 27(3): 25-28.
DING Qi, WEI Ping, XIAO Xianci. Estimation and analysis of DOA based on fourth-order cumulant[J]. ACTA Electronica SINICA, 1999, 27(3): 25-28. DOI: 10.3321/j.issn:0372-2112.1999.03.008 |
| [8] | ZHANG Xin, LIU Xiaoming, YU Haixia, et al. Improved MUSIC algorithm for DOA estimation of coherent signals via toeplitz and fourth-order-cumulants[J]. International Journal of Control and Automation, 2015, 8(10): 261-272. DOI: 10.14257/ijca.2015.8.10.25 |
| [9] |
陈建, 王树勋. 基于高阶累积量虚拟阵列扩展的DOA估计[J].
电子与信息学报, 2007, 29(5): 1041-1044.
CHEN Jian, WANG Shuxun. DOA estimation of virtual array extension based on fourth-order cumulant[J]. Journal of Electronics and Information Technology, 2007, 29(5): 1041-1044. DOI: 10.3969/j.issn.1671-5896.2006.04.001 |
| [10] | AKKAR S, HARABI F, GHARSALLAH A. MUSIC like algorithms for fast direction of arrival estimation [C]// 1st International Conference on Advanced Technologies for Signal and Image Processing. Sousse: IEEE, 2014: 550-554. DOI: 10.1109/ATSIP.2014.6834675. |
| [11] | LIE S, LEYMAN A R, CHEW Y H. Fourth-order and weighted mixed order direction-of-arrival estimators[J]. IEEE Signal Processing Letters, 2006, 13(11): 691-694. DOI: 10.1109/LSP.2006.879456 |
| [12] | WANG Qing, CHEN Hua, ZHAO Guohuang, et al. An improved direction finding algorithm based on toeplitz approximation[J]. Sensors, 2013, 13(1): 746-757. DOI: 10.3390/s130100746 |
| [13] | LIAO Bin, CHAN S C. A cumulant-based method for direction finding in uniform linear arrays with mutual coupling[J]. IEEE Antennas and Wireless Propagation Letters, 2014, 13: 1717-1720. DOI: 10.1109/LAWP.2014.2352939 |
| [14] |
宋海岩, 朴胜春. 基于高阶累积量矩阵组正交联合对角化的高分辨率方位估计方法[J].
电子与信息学报, 2010, 32(4): 967-972.
SONG Haiyan, PIAO Shengchun. DOA estimation method based on orthogonal joint diagonalization of high-order cumulant[J]. Journal of Electronics and Information Technology, 2010, 32(4): 967-972. DOI: 10.3724/SP.J.1146.2008.01176 |
| [15] | LI Wenxing, MAO Xiaojun, YU Wenhua, et al. An effective technique for enhancing direction finding performance of virtual arrays[J]. International Journal of Antenna and Propagation, 2014(3): 1-7. DOI: 10.1155/2014/728463 |
| [16] | SHAN Zhilong, YUM T S P. A conjugate augmented approach to direction-of-arrival estimation[J]. IEEE Transactions on Signal Processing, 2005, 53(11): 4104-4109. DOI: 10.1109/TSP.2005.857012 |
| [17] | BREWER J W. Kronecker products and matrix calculus in system theory[J]. IEEE Transaction on Circuits and Systems, 1978, 25(9): 772-781. DOI: 10.1109/TCS.1978.1084534 |
 2017, Vol. 49
2017, Vol. 49


