协作中继技术作为多天线技术的一种扩展,通过形成虚拟的MIMO技术获得协作分集,扩大信号传输范围,已经成为研究热点.文献[1]中的放大转发 (amplify-and-forward,AF) 和解码转发 (decode-and-forward,DF) 两种中继协议已经表明,通过中继共享用户的天线,可以提高系统容量,降低系统随信道变化的敏感性.然而,由于实际通信系统的半双工限制,协作中继在提高无线传输性能的同时也带来了频谱效率的损失.为此,文献[2]提出了只需两个时隙即可完成信息交互的双向中继传输方案;文献[3]详细推导了AF模式和DF模式下双向中继系统的容量,并与单向系统的容量做了对比,研究表明,双向中继较单向中继能够获得更高的吞吐量.由于DF双向中继需在中继端进行复杂的额外操作,而AF协议只需对双向接入信号进行简单的功率控制,因而简单、易行的AF协议得到更多的关注.针对双向AF中继系统,文献[4-5]研究了双向中继系统中单一用户的中断概率问题.而在实际中,双向中继系统任意一个节点发生了中断,双向中继传输即为中断.为此,文献[6-10]分析了双向中继中两个用户的联合中断概率问题.但文献[6-8]的研究均是基于大信噪比假设,文献[9-10]只考虑系统具有相同的信道条件.更进一步,文献[11-12]对信道具有互易特性但两端信道条件不对称的系统进行了中断概率分析.为了优化系统性能,有研究人员[7, 9, 11, 13]对双向中继系统中的功率分配问题进行了研究.但上述文献都只考虑了一种特殊的网络模型,即系统上行阶段和下行阶段的各个信道具有相同的信道条件.另外,文献[14]也指出非对称性对双向中继系统中的许多性能指标,如系统中断概率、误码率等,均有不同程度的影响.对于非对称信道问题,文献[15]针对物理层网络编码在非对称双向中继信道中的误码率性能进行了分析.但是,对非对称信道条件双向中继放大转发协议的中断概率性能未见报导.
基于此,本文考虑一般化的双向中继模型,即信道条件非对称,研究影响系统中断性能的最主要因素,从双向传输的角度,以降低非对称系统中断概率为目标来实现节点间的功率分配,达到系统中断性能的优化,并且仿真验证该方案对系统性能的改善效果.
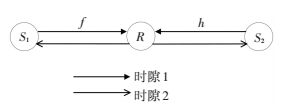
1 非对称双向中继信道模型 1.1 传统三节点对称双向中继信道模型首先给出传统三节点双向中继通信系统模型,中继节点处采取放大转发协议,系统建模如图 1所示.
|
图 1 传统三节点系统模型 Figure 1 Traditional three-node system model |
图 1中,假设两用户节点没有直接进行通信的信道,用户节点S1与用户节点S2通过中继R互相传递信号.节点S1向对方广播的信号为x1,节点S2向对方广播的信号为x2.假设信道具有互易性,h、f分别为S1-R信道与S2-R信道的信道衰落系数,两者相互独立. p1、p2、pR分别表示S1、S2和R的发射功率,且满足p1+p2+pR≤pt. n1、n2、nR分别表示S1、S2和R处的高斯白噪声 (AWGN),设其均值为0,方差为1.为了分析方便这里将S1端与S2端的距离归一化为1,S1-R信道链路长度为d且其满足0<d<1.
1.2 非对称因子在实际通信系统中,信道状况受很多因素影响,信道条件并不是理想的.若只考虑信道中的小尺度衰落,可将信道视为对称的,但是若信道中还有阴影衰落、路径损耗等,此时各个信道条件的不同会导致信道非对称.本节主要考虑系统中含1条或2条不可靠信道,从而导致非对称的情况 (此处不可靠信道是相对而言的,指的是其信道条件比其他信道差,后文亦同).
为了表示信道非对称程度,引入2个参数:a,b称为非对称因子.当系统中有1条不可靠信道时,该不可靠信道需要在信道衰落系数基础上乘以非对称因子a; 当系统中有2条不可靠信道时,这2条不可靠信道都要乘以非对称因子b.由于信号在信道中传输只可能会产生衰落,所以0<a, b≤1,当其等于1时,即表示信道对称. a,b越小,系统非对称程度越严重,传输性能越不可靠.为比较不同情况下非对称双向中继通信系统的中断性能,介绍一下a,b之间的约束关系.为了确保系统在含有1条不可靠信道与2条不可靠信道时,在传输过程中系统总的接收能量相同,有p+p+p+a2p=p+p+b2p+b2p(其中p为各节点处的功率,假设均相等),化简得1+a2=2b2,进而得到a,b之间的关系为
| $ b = \sqrt {\left( {1 + {a^2}} \right)/2} . $ | (1) |
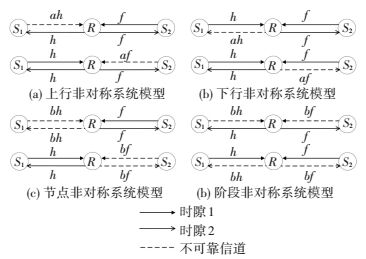
根据不可靠信道可能出现的情况,非对称双向中继系统可分为上行非对称、下行非对称、节点非对称和阶段非对称. 图 2为4种非对称双向中继信道模型,除存在不可靠信道外, 其余信道条件与1.1节中相同.对于前3种模型只讨论用户节点S1与中继R之间含非对称因子的情况,节点S2与R之间情形分析相同.
|
图 2 4种非对称双向中继信道模型 Figure 2 Four cases of asymmetric two-way relay channel model |
下面以上行非对称双向中继信道模型为例对系统中断性能进行分析.第一时隙用户节点S1与S2同时向中继R发送各自信息,中继R处接收信号表示为
| $ {y_{\rm{R}}} = ah\sqrt {{p_1}} {x_1} + f\sqrt {{p_2}} {x_2} + {n_{\rm{R}}}. $ |
第二时隙中继R将接收信号放大之后广播至用户节点S1和S2,两用户的接收信号为
| $ \begin{array}{l} {{y'}_1} = ak{h^2}\sqrt {{p_1}} {x_1} + khf\sqrt {{p_2}} {x_2} + kh{n_{\rm{R}}} + {n_1},\\ {{y'}_2} = akhf\sqrt {{p_1}} {x_1} + k{f^2}\sqrt {{p_2}} {x_2} + kf{n_{\rm{R}}} + {n_2}. \end{array} $ |
其中k为中继采用放大转发协议的放大因子,其值为
| $ k = \sqrt {\frac{{{p_{\rm{R}}}}}{{{a^2}{h^2}{p_1} + {f^2}{p_2} + 1}}} . $ |
去除自身干扰后用户节点S1与S2的接收信噪表示为
| $ \left\{ \begin{array}{l} {\gamma _1} = \frac{{{p_2}{p_{\rm{R}}}{h^2}{f^2}}}{{\left( {{a^2}{p_1} + {p_{\rm{R}}}} \right){h^2} + {p_2}{f^2} + 1}},\\ {\gamma _2} = \frac{{{a^2}{p_1}{p_{\rm{R}}}{h^2}{f^2}}}{{{a^2}{p_1}{h^2} + \left( {{p_2} + {p_{\rm{R}}}} \right){f^2} + 1}}. \end{array} \right. $ |
其他3种情况的分析过程类似,只给出每种情形的用户端接收信噪比表达式.
下行非对称:
| $ \left\{ \begin{array}{l} {\gamma _1} = \frac{{{a^2}{p_2}{p_{\rm{R}}}{h^2}{f^2}}}{{\left( {{p_1} + {a^2}{p_{\rm{R}}}} \right){h^2} + {p_2}{f^2} + 1}},\\ {\gamma _2} = \frac{{{p_1}{p_{\rm{R}}}{h^2}{f^2}}}{{{p_1}{h^2} + \left( {{p_2} + {p_{\rm{R}}}} \right){f^2} + 1}}. \end{array} \right. $ | (2) |
节点非对称:
| $ \left\{ \begin{array}{l} {\gamma _1} = \frac{{{b^2}{p_2}{p_{\rm{R}}}{h^2}{f^2}}}{{\left( {{b^2}{p_1} + {b^2}{p_{\rm{R}}}} \right){h^2} + {p_2}{f^2} + 1}},\\ {\gamma _2} = \frac{{{b^2}{p_1}{p_{\rm{R}}}{h^2}{f^2}}}{{{b^2}{p_1}{h^2} + \left( {{p_2} + {p_{\rm{R}}}} \right){f^2} + 1}}. \end{array} \right. $ |
阶段非对称 (上):
| $ \left\{ \begin{array}{l} {\gamma _1} = \frac{{{b^2}{p_2}{p_{\rm{R}}}{h^2}{f^2}}}{{\left( {{b^2}{p_1} + {p_{\rm{R}}}} \right){h^2} + {b^2}{p_2}{f^2} + 1}},\\ {\gamma _2} = \frac{{{b^2}{p_1}{p_{\rm{R}}}{h^2}{f^2}}}{{{b^2}{p_1}{h^2} + \left( {{b^2}{p_2} + {p_{\rm{R}}}} \right){f^2} + 1}}. \end{array} \right. $ |
阶段非对称 (下):
| $ \left\{ \begin{array}{l} {\gamma _1} = \frac{{{b^2}{p_2}{p_{\rm{R}}}{h^2}{f^2}}}{{\left( {{p_1} + {b^2}{p_{\rm{R}}}} \right){h^2} + {p_2}{f^2} + 1}},\\ {\gamma _2} = \frac{{{b^2}{p_1}{p_{\rm{R}}}{h^2}{f^2}}}{{{p_1}{h^2} + \left( {{p_2} + {b^2}{p_{\rm{R}}}} \right){f^2} + 1}}. \end{array} \right. $ |
中断概率是保证系统进行可靠信息传输的重要指标,可将其定义为当链路间信噪比γ小于信道要求的门限γth时,通信即会发生中断.则系统中断概率可表示为Pout=P(γ1<γth∪γ2<γth).
1.4 实验结果与分析为了比较4种非对称信道的中断性能,对其进行仿真分析.考虑中继R位于两用户节点连线的中间位置 (d=0.5), 各节点处功率均相等.信道衰落系数h, f服从瑞利分布,设u=h2,v=f2,则u、v分别服从均值为Ωh, Ωf且Ωh=d-λ, Ωf=(1-d)-λ的指数分布,λ为路径损耗因子,这里取值为4.
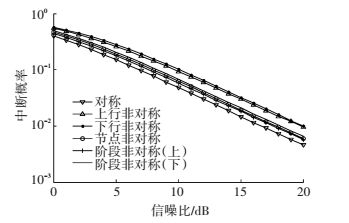
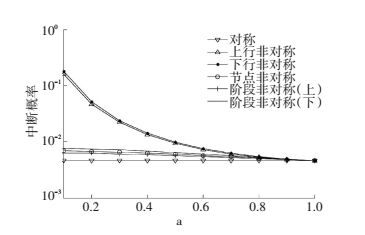
首先假设非对称因子a=0.5,根据式 (1) 可计算出b=0.790 6,对非对称与对称双向中继系统的中断概率进行仿真,如图 3所示. 图 3中系统的中断概率随信噪比的变化而变化,可以看出:下行非对称中断概率最大;其次为上行非对称;阶段非对称 (下) 要好于前两者;在各种非对称情况中,阶段非对称 (上) 性能最好.在给定系统信噪比的情况下,分析非对称因子变化时,对称和各种非对称情况下中断概率的仿真情形,如图 4所示.从图 4中可以看出:上行非对称和下行非对称随a的增大中断概率在降低,而节点非对称、阶段非对称的变化并不明显;在整个变化区间内下行非对称性能最差,上行非对称次之.
|
图 3 瑞利信道下a、b一定且信噪比变化时系统的中断概率对比 Figure 3 Comparison of the system outage probability in Rayleigh channel when a, b are constant and RSN is variable |
|
图 4 瑞利信道下信噪比一定且a、b变化时系统的中断概率对比 Figure 4 Comparison of the system outage probability in Rayleigh channel when RSN is constant and a, b are variable |
比较图 3、4,下行非对称占用1条下行信道,它的中断概率最大;上行非对称占用1条上行信道,性能次之;阶段非对称 (下) 占用2条下行信道,节点非对称占用1条上行信道与1条下行信道,而阶段非对称 (上) 占用2条上行信道,它的中断概率最小.从中可以看出,1条不可靠信道比2条不可靠信道对系统的中断概率影响大;下行不可靠信道比上行不可靠信道对系统的中断概率影响大;下行信道越不可靠,越可能发生中断,对通信的影响越大.通过对比可以看出下行信道的非对称对双向中继系统中断性能影响最大,下面将针对这一情形做进一步研究来改善系统的中断性能.
2 功率分配优化针对上文对4种非对称双向中继信道中断概率的分析,得到一条下行信道为不可靠信道时对系统的中断性能影响最大,为了改善这一问题本节考虑在该情形下,利用信道状态信息的用户节点功率分配方案来优化系统的中断性能.系统模型见图 2(b).
2.1 下行非对称双向中继信道中断概率分析下面将详细推导上文中下行非对称情况中断概率具体表达式.根据式 (2) 用户端接收信噪比可进一步表示如下:
| $ \begin{array}{l} {\gamma _1} = \frac{{{a^2}{p_2}{p_{\rm{R}}}uv}}{{\left( {{p_1} + {a^2}{p_{\rm{R}}}} \right)u + {p_2}v + 1}} \approx \frac{{{a^2}{p_2}{p_{\rm{R}}}uv}}{{\left( {{p_1} + {a^2}{p_{\rm{R}}}} \right)u + {p_2}v}} = \\ \;\;\;\;\;\;{p_{\rm{R}}}\frac{{{a^2}u\frac{{{p_2}v}}{{{p_1} + {a^2}{p_{\rm{R}}}}}}}{{u + \frac{{{p_2}v}}{{{p_1} + {a^2}{p_{\rm{R}}}}}}} < {p_{\rm{R}}}\min \left( {\frac{{{a^2}{p_2}v}}{{{p_1} + {a^2}{p_{\rm{R}}}}},{a^2}u} \right), \end{array} $ |
同理可得
| $ {\gamma _2} < {p_{\rm{R}}}\min \left( {\frac{{{p_1}u}}{{{p_2} + {p_{\rm{R}}}}},v} \right). $ |
设
| $ \begin{array}{l} {P_{{\rm{out}}}} = P\left( {{\gamma _1} < {\gamma _{{\rm{th}}}} \cup {\gamma _2} < {\gamma _{{\rm{th}}}}} \right) = \\ \;\;\;\;\;\;\;\;1 - P\left( {{\gamma _1} > {\gamma _{{\rm{th}}}} \cup {\gamma _2} > {\gamma _{{\rm{th}}}}} \right) = \\ \;\;\;\;\;\;\;\;1 - P\left( {\min \left( {{\gamma _1},{\gamma _2}} \right) > {\gamma _{{\rm{th}}}}} \right) = \\ \;\;\;\;\;\;\;\;1 - P\left( {\min \left( {{a^2}{\psi _1}v,{\psi _2}u,{a^2}u,v} \right) > \frac{{{\gamma _{{\rm{th}}}}}}{{{p_{\rm{R}}}}}} \right). \end{array} $ |
注意到此时min (a2ψ1v, ψ2u, a2u, v) 可做分段处理,等同于
| $ \begin{array}{l} \min \left( {{\psi _1}u,v} \right),{a^2}{p_2} \ge {p_1} + {a^2}{p_{\rm{R}}},\\ \min \left( {{a^2}{\psi _1}v,{a^2}u} \right),{p_1} \ge {a^2}\left( {{p_2} + {p_{\rm{R}}}} \right),\\ \min \left( {{a^2}{\psi _1}v,{\psi _2}u} \right),{p_1} \le {a^2}\left( {{p_2} + {p_{\rm{R}}}} \right),{a^2}{p_2} \le {p_1} + {a^2}{p_{\rm{R}}}. \end{array} $ |
设ψ′1=min (a2ψ1, 1), ψ′2=min (ψ2, a2) 则
| $ \begin{array}{l} \min \left( {{a^2}{\psi _1}v,{\psi _2}u,{a^2}u,v} \right) = \min \left( {{{\psi '}_1}v,{{\psi '}_2}u} \right),\\ P\left( {\min \left( {{a^2}{\psi _1}v,{\psi _2}u,{a^2}u,v} \right) > {\gamma _{{\rm{th}}}}/{p_{\rm{R}}}} \right) = \\ \;\;\;P\left( {\min \left( {{{\psi '}_1}v,{{\psi '}_2}u} \right) > {\gamma _{{\rm{th}}}}/{p_{\rm{R}}}} \right) = \\ \;\;\;P\left( {{{\psi '}_2}u > {\gamma _{{\rm{th}}}}/{p_{\rm{R}}},{{\psi '}_2}u \le {{\psi '}_1}u} \right) + \\ \;\;\;P\left( {{{\psi '}_1}v > {\gamma _{{\rm{th}}}}/{p_{\rm{R}}},{{\psi '}_1}u \le {{\psi '}_2}u} \right) = \\ \;\;\;\int_{{\gamma _{{\rm{th}}}}/{p_{\rm{R}}}{{\psi '}_2}}^\infty {\int_{{{\psi '}_2}u \le {{\psi '}_1}}^\infty {{f_v}\left( x \right){\rm{d}}x{f_u}\left( u \right){\rm{d}}u} } + \\ \;\;\;\int_{{\gamma _{{\rm{th}}}}/{p_{\rm{R}}}{{\psi '}_1}}^\infty {\int_{{{\psi '}_1}v \le {{\psi '}_2}}^\infty {{f_u}\left( x \right){\rm{d}}x{f_v}\left( v \right){\rm{d}}v} } = \\ \;\;\;{{\rm{e}}^{ - \left( {\frac{1}{{{{\psi '}_1}{\Omega _f}}} + \frac{1}{{{{\psi '}_2}{\Omega _{\rm{h}}}}}} \right)\frac{{{\gamma _{{\rm{th}}}}}}{{{p_{\rm{R}}}}}}}. \end{array} $ |
其中fu(u)=
考虑在高信噪比区域 (pR→
| $ \begin{array}{l} {P_{{\rm{out}}}} = 1 - {{\rm{e}}^{ - \left( {\frac{1}{{{{\psi '}_1}{\mathit{\Omega }_f}}} + \frac{1}{{{{\psi '}_2}{\mathit{\Omega }_{\rm{h}}}}}} \right)\frac{{{\gamma _{{\rm{th}}}}}}{{{p_{\rm{R}}}}}}} \approx \\ \;\;\;\;\;\;\;\;\;1 - \left( {1 - \left( {\frac{1}{{{{\psi '}_1}{\mathit{\Omega }_f}}} + \frac{1}{{{{\psi '}_2}{\mathit{\Omega }_{\rm{h}}}}}} \right)\frac{{{\gamma _{{\rm{th}}}}}}{{{p_{\rm{R}}}}}} \right) = \\ \;\;\;\;\;\;\;\;\;\left( {\frac{1}{{{{\psi '}_1}{\mathit{\Omega }_f}}} + \frac{1}{{{{\psi '}_2}{\mathit{\Omega }_{\rm{h}}}}}} \right)\frac{{{\gamma _{{\rm{th}}}}}}{{{p_{\rm{R}}}}}. \end{array} $ |
下面对ψ′1,ψ′2进行具体的分析:当a2p2≥p1+a2pR时,ψ′1=1,ψ′2=
本节研究在总功率一定的情况下,降低下行非对称系统中断概率的各用户节点功率分配问题.由上述分析,将根据以下三种情况进行讨论:
1) 当p1≤a2(p2+pR),a2p2≤p1+a2pR时,由于上述理论推导的目标函数较为复杂,这一部分将对其进行缩放,得到中断概率的上界Pout=
| $ \begin{array}{l} \mathop {\min }\limits_{{p_1},{p_2},{p_{\rm{R}}}} \frac{{{\gamma _{{\rm{th}}}}}}{{{p_{\rm{R}}}}}\left( {\frac{{{p_1} + {p_{\rm{R}}}}}{{{a^2}{p_2}{\mathit{\Omega }_f}}} + \frac{{{p_2} + {p_{\rm{R}}}}}{{{p_1}{\mathit{\Omega }_h}}}} \right),\\ \;\;\;\;\;\;\;\;{\rm{s}}{\rm{.t}}{\rm{.}}\;{p_1} + {p_2} + {p_{\rm{R}}} = {p_{\rm{t}}},\\ \;\;\;\;\;\;\;\;{p_1},{p_2},{p_{\rm{R}}} \ge 0. \end{array} $ |
得到功率分配的最优解为
| $ \begin{array}{l} {p_1} = \frac{{a\varepsilon }}{{a\varepsilon + \sqrt {2a\varepsilon } + 1}}{p_{\rm{t}}},\\ {p_2} = \frac{1}{{a\varepsilon + \sqrt {2a\varepsilon } + 1}}{p_{\rm{t}}},\\ {p_{\rm{R}}} = \frac{{\sqrt {2a\varepsilon } }}{{a\varepsilon + \sqrt {2a\varepsilon } + 1}}{p_{\rm{t}}}. \end{array} $ |
其中ε=
2) 当a2p2≥p1+a2pR时,ε≤a+a3-
| $ \begin{array}{l} \mathop {\min }\limits_{{p_1},{p_2},{p_{\rm{R}}}} \frac{{{\gamma _{{\rm{th}}}}}}{{{p_{\rm{R}}}}}\left( {\frac{1}{{{\mathit{\Omega }_f}}} + \frac{{{p_2} + {p_{\rm{R}}}}}{{{p_1}{\mathit{\Omega }_h}}}} \right),\\ \;\;\;{\rm{s}}{\rm{.t}}{\rm{.}}\;{p_1} + {p_2} + {p_{\rm{R}}} = {p_{\rm{t}}},\\ \;\;\;\;\;\;\;{p_1},{p_2},{p_{\rm{R}}} \ge 0. \end{array} $ |
得到功率分配的最优解为
| $ \begin{array}{l} {p_1} = \frac{{{a^2}\varepsilon }}{{\sqrt {{a^2} + 1} \left( {\varepsilon \sqrt {{a^2} + 1} + \sqrt {{a^2} + {\varepsilon ^2}} } \right)}}{p_{\rm{t}}},\\ {p_2} = \frac{{2\varepsilon + \sqrt {\left( {{a^2} + 1} \right)\left( {{a^2} + {\varepsilon ^2}} \right)} }}{{2\sqrt {{a^2} + 1} \left( {\varepsilon \sqrt {{a^2} + 1} + \sqrt {{a^2} + {\varepsilon ^2}} } \right)}}{p_{\rm{t}}},\\ {p_{\rm{R}}} = \frac{{\sqrt {{a^2} + {\varepsilon ^2}} }}{{2\left( {\varepsilon \sqrt {{a^2} + 1} + \sqrt {{a^2} + {\varepsilon ^2}} } \right)}}{p_{\rm{t}}}. \end{array} $ |
此时系统中断概率的最小值出现在p2=(p1+a2pR)/a2处.
3) 当p1≥a2(p2+pR) 时,ε≥a+a3+
| $ \begin{array}{l} \mathop {\min }\limits_{{p_1},{p_2},{p_{\rm{R}}}} \frac{{{\gamma _{{\rm{th}}}}}}{{{p_{\rm{R}}}}}\left( {\frac{{{p_1} + {a^2}{p_{\rm{R}}}}}{{{a^2}{p_2}{\mathit{\Omega }_f}}} + \frac{1}{{{a^2}{\mathit{\Omega }_f}}}} \right),\\ \;\;\;{\rm{s}}{\rm{.t}}{\rm{.}}\;{p_1} + {p_2} + {p_{\rm{R}}} = {p_{\rm{t}}},\\ \;\;\;\;\;\;\;{p_1},{p_2},{p_{\rm{R}}} \ge 0. \end{array} $ |
得到功率分配的最优解为
| $ \begin{array}{l} {p_1} = \frac{{{a^2}}}{{{a^2} + 1}}{p_{\rm{t}}},\\ {p_2} = \frac{{\sqrt {2{a^2}} }}{{\left( {{a^2} + 1} \right)\left( {\sqrt {2{a^2}} + \sqrt {{a^2} + {\varepsilon ^2}} } \right)}},\\ {p_{\rm{R}}} = \frac{{\sqrt {{a^2} + {\varepsilon ^2}} }}{{\left( {{a^2} + 1} \right)\left( {\sqrt {2{a^2}} + \sqrt {{a^2} + {\varepsilon ^2}} } \right)}}{p_{\rm{t}}}. \end{array} $ |
此时系统中断概率的最小值出现在p1=a2(p2+pR) 处.
3 性能仿真与分析为了说明下行信道非对称系统的中断性能,本节给出一些仿真结果.信道参数设置与上节相同. 图 5显示了在非对称因子取不同值时,等功率分配情况下,系统中断概率随信噪比变化的曲线.从图 5观察到,随着非对称因子的增大,系统的中断概率在降低,与第1节中分析结果相同.此外中断概率的理论值、近似值与仿真值比较吻合,尤其是在大信噪比的情况下三者完全重合,说明了理论分析的正确性.

|
图 5 不同a时中断概率随信噪比变化曲线 Figure 5 Effect of a on the outage probability versus RSN |
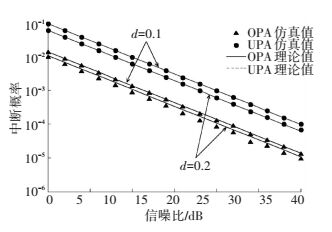
图 6分别仿真对比了d=0.1和d=0.2时系统的中断性能.可以看出,随着信噪比逐渐增大,系统的中断概率降低,并且在整个范围内本文优化功率分配方案 (OPA) 的中断概率一直小于等功率分配方案 (UPA).在信噪比RSN=20 dB,d=0.1时,OPA在中断概率性能上较UPA相比约有8 dB的增益.同时也可以看出,图 6中的理论值与仿真值是一致的,验证了该功率分配方案的正确性.
|
图 6 OPA与UPA的中断性能比较1 Figure 6 Comparison of outage performance between OPA and UPA 1 |
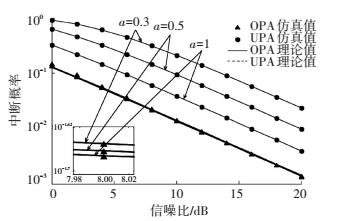
图 7所示为d=0.1的条件下,非对称因子取不同值时本文优化功率分配方案与等功率分配方案的对比图.为了更清楚地看出仿真效果,子图为优化功率分配方案仿真曲线的放大.从图 7可以看出, 非对称因子越小即下行信道越不可靠时,OPA与UPA整体的中断概率都随着非对称因子的减小而增大.同时随着非对称因子的减小,OPA相比于UPA在中断概率一定的条件下功率增益增大.说明该优化功率分配方案在下行非对称信道越不可靠时带来的性能增益越好,改善了下行非对称信道的中断性能.
|
图 7 OPA与UPA的中断性能比较2 Figure 7 Comparison 2 of outage performance between OPA and UPA |
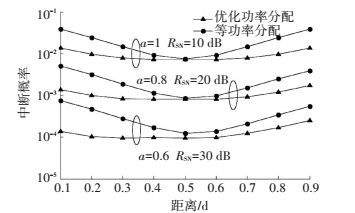
图 8给出了系统中断概率与d之间的关系曲线,不失一般性地将两个用户节点间距离归一化为1.可以看出,本文优化功率分配方案较等功率分配方案有中断性能的优势,尤其是在下行非对称信道条件下,随着非对称因子的减小,优势更加显著.
|
图 8 不同d时OPA与UPA的中断性能比较 Figure 8 Comparison of outage performance between OPA and UPA in different d |
从上述分析中可以得出,本文提出的优化功率分配方案改善了由下行信道非对称带来的系统中断性能下降的问题,但较等功率而言增加了计算的复杂性. CPU的运行时间可以用来作为比较所提方案与等功率方案的复杂度.对2种方案的运算时间进行计算,所用计算机平台为因特尔i5处理器、主频2.50 GHz、32位Windows7专业版下的Matlab R2012a仿真软件. 100次计算的平均结果为:本方案平均运算时间0.129 302 s,等功率方案平均运算时间0. 123 191 s.可以看出本文提出的优化功率分配方案较等功率分配方案在仿真时间上有所增加,时间代价很小,但本文方案可以有效的提高系统的中断性能.
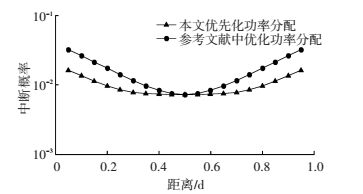
为了进一步说明本文所提方案的优势,在a=1的情况下与文献[5]中的优化功率分配方案进行对比,仿真效果如图 9所示.由图 9可以看出,本文的优化功率分配方案的中断概率在d的取值范围内优于文献[5]中的方案,尤其是在中继节点非常靠近某一用户节点的情况下.这是因为本文所提出的方案会根据信道增益的取值情况,将中断概率作为分段函数进行处理得到3种不同的优化区间分配值,对信道状态的变化具有更好的适应性,这也说明了本文提出的优化功率分配方案在信道对称的情况下也会有很好的性能.
|
图 9 2种方案中断概率与d的关系对比 Figure 9 The relationship between outage probability and d of two schemes |
本文从双向传输的角度研究了基于放大转发协议的非对称双向中继系统中断概率问题.首先引入了非对称因子,考虑4种非对称情况,仿真分析了非对称信道影响系统中断性能下降的最主要原因,得出下行信道非对称对系统中断性能影响最大;然后针对下行非对称问题,在理论分析得出系统中断概率表达式和渐进表达式的基础上,以优化系统中断性能为目标,提出一种基于信道状态信息的用户节点功率分配方案,该方案虽然增加了运算量但对系统的中断性能有了很大的提升.同时由仿真可以看出,较等功率分配方案相比,非对称因子越小,所提方案的性能优势越加显著,即使是在信道对称的情况下本文所提出的方案因对信道状态的变化具有更好的适应性,也会有中断性能的优势.
| [1] | SENDONARIS A, ERKIP E, AAZHANG B. User cooperation diversity. Part Ⅱ. Implementation aspects and performance analysis[J]. IEEE Transactions on Communications, 2003, 51(11): 1939-1948. DOI: 10.1109/TCOMM.2003.819238 |
| [2] | RANKOV B, WITTNEBEN A. Spectral efficient protocols for half-duplex fading relay channels[J]. IEEE Journal on Selected Areas in Communications, 2007, 25(2): 379-389. DOI: 10.1109/JSAC.2007.070213 |
| [3] | NAM W, CHUNG S Y, LEE Y H. Capacity bounds for two-way relay channels[C]// International Zurich Seminar on Communications. Zurich: IEEE, 2008:144-147. DOI:10.1109/IZS.2008.4497296. |
| [4] | LI Qiang, TING S H, PANDHARIPANDE A, et al. Adaptive two-way relaying and outage analysis[J]. IEEE Transactions on Wireless Communications, 2009, 8(6): 3288-3299. DOI: 10.1109/TWC.2009.081213 |
| [5] |
刘通, 陈前斌, 唐伦, 等. Two-way中继系统中基于最小化中断概率的功率分配策略[J].
计算机应用研究, 2011, 28(3): 1108-1110.
LIU Tong, CHEN Qianbin, TANG Lun, et al. Optimal power allocation scheme based on minimizing outage probability in Two-way relay system[J]. Application Research of Computers, 2011, 28(3): 1108-1110. DOI: 10.3969/j.issn.1001-3695.2011.03.089 |
| [6] | JU M C, KIM I M. Relay selection with analog network coding in bidirectional networks Communications[C]//. Kingston: IEEE, 2010:293-296. DOI:10.1109/BSC.2010.5472937. |
| [7] | YI Zhihang, JU M C, KIM I M. Outage probability and optimum power allocation for analog network coding[J]. IEEE Transactions on Wireless Communications, 2011, 10(2): 407-412. DOI: 10.1109/TWC.2011.120810.100873 |
| [8] | LONG Yanshan, GAO Yuanyuan, GUO Mingxi, et al. Outage analysis of two-way AF relaying systems with imperfect CSI and multiple interferers over Nakagami-m fading channels[C]// IEEE International Conference on Information Science and Technology. Shenzhen: IEEE, 2014:535-538. DOI:10.1109/ICIST.2014.6920534. |
| [9] | REN Zheng, CHANG Yongyu, ZHANG Yongliang, et al. Outage probability of joint relay selection and power allocation for two-way relay networks over rayleigh fading channels[C]// Vehicular Technology Conference (VTC Spring). Yokohama: IEEE, 2012:1-5. DOI:10.1109/VETECS.2012.6239937. |
| [10] | ZHANG Chensi, GE Jianhua, LI Jing, et al. A unified approach for calculating outage performance of two-way AF relaying over fading channels[J]. IEEE Transactions on Vehicular Technology, 2015, 64(3): 1218-1229. DOI: 10.1109/TVT.2014.2329853 |
| [11] | BAGHERI H, ARDAKANI M, TELLAMBURA C. Resource allocation for two-way AF relaying with receive channel knowledge[J]. IEEE Transactions on Wireless Communications, 2012, 11(6): 2002-2007. DOI: 10.1109/TWC.2012.032812.111476 |
| [12] | LOU Sijia, YANG Longxiang. Performance analysis of joint relay selection and power allocation for two-way relay channels[C]//Proceedings of the International Conference on Computer Networks & Communication Engineering. IEEE, 2013:455-460. DOI:10.2991/iccnce.2013.114. |
| [13] | YANG Yanping, CHEN Wei, LI Ou, et al. Joint rate and power adaptation for amplify-and-forward two-way relaying on analog network coding[J]. IEEE Access, 2016, 4: 1-1. DOI: 10.1109/ACCESS.2016.2566878 |
| [14] | POPOVSKI P, YOMO H. Bi-directional amplification of throughput in a wireless multi-hop network[J]. Electrical Engineering/Electronics Computer Communications & Information Technology Association, 2006, 2: 588-593. DOI: 10.1109/VETECS.2006.1682892 |
| [15] |
李博. 物理层网络编码及其在非对称双向中继通信中的性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2013.
LI Bo. Research on physical-layer network coding and the performance in asymmetric two-way relay communications[D]. Harbin: Harbin Institute of Technology, 2013. |
 2017, Vol. 49
2017, Vol. 49


