肺癌是威胁人类生命健康的恶性肿瘤疾病,中国目前总体肺癌发病率增长了19.48%,这很可能是加剧的环境污染问题如大规模雾霾引起的[1].早期诊断能大幅度提高病患存活率,但目前早期诊断率仅15%[2].常见肺癌早期诊断手段包括CT成像与光学内窥镜.CT成像拥有密度分辨率高、操作简单等优势,但传统CT只能提供单层的断面信息,不直观,且在诊断过程中病人需承受大量放射辐射;光学内窥镜可在零辐射下观察到管腔内部真实纹理色彩,但操作上要比CT成像复杂得多.
随着计算机辅助诊断技术的发展,虚拟支气管镜VB[3](virtual bronchoscopy) 技术在肺癌诊断领域正逐渐得以普遍应用.该技术利用从CT数据中重建的气管模型,对肺部疾病诊断有重大意义.临床表明VB不仅可以显示有无气道异常如支气管狭窄等,还可以配合导航系统引导经支气管镜肺活检,明显提高支气管镜在肺部外周病灶诊断效率.相对于传统内窥镜而言,VB引导下的导航技术具有以下优点:1) 定位准确,诊断效能高;2) 可快速引导支气管镜,缩短检查时间,减少病患痛苦;3) 可减少支气管镜检查次数;4) 可提供自由的虚拟观测角度,降低支气管异常的辨别难度;5) 可部分代替X线引导的支气管镜活检,减少辐射;6) 可避免盲目穿刺,降低并发症发生率.大量文献证实虚拟内窥镜能在不失诊断准确率的基础上,保障诊断的微创性[4-5].
在虚拟内窥镜实现过程中,快速的骨架线提取一直是其中的难点和要点.而在VB中,一个良好提取的骨架线不仅可以提供直观的支气管拓扑结构,还可以为管腔内浏览起到引导作用.与人体其他管腔如结肠、血管相比,支气管结构更为复杂[6],体现在:1) 复杂的拓扑结构,拥有多级分支,多通路;2) 各级分支粗细不一;3) 个体差异性,不同人支气管虽在级数上有一定相似性,但大小和分支位置却存在差异.目前三维骨架提取方式主要有距离变换法、中轴变换法和腐蚀细化算法.然而由于支气管的复杂性,这些方式在支气管骨架线的提取上都略显性能不足.随着当今4DCT[7]数据的逐步普及,传统方法的运算速度更显得不尽人意.
本文提出一种基于腐蚀细化的改进三维骨架线提取方法,以克服传统腐蚀细化方法中复杂度高、耗时长的问题.本方法充分利用了当今计算机多核以及高内存的优势,在传统三维腐蚀过程中引入LUT.相关实验证实,本方法能够显著提高骨架线的提取速度.
1 骨架线基本定义与现有方法综述 1.1 骨架线基本定义骨架 (Skeleton) 是指与原物体具有一致连通性和拓扑结构的细曲线的一种理想表示,就是位于物体内部,且能体现其拓扑特征的简化图形[8].在三维情况下提取的骨架线需要满足如下要求[9]:1) 连通性,骨架线应与目标物体拥有相同的连通性;2) 居中性,骨架线尽量保持在管腔的中央;3) 单体素性,组成骨架线的体素要求为单元宽度.对于简单的柱状组织,中心线只有唯一的一条,而对于支气管树或血管树这种复杂的管状结构,中心线会有多条,也被称作为骨架线.
1.2 现有方法综述就目前而言,二维的中心线提取算法已经相对成熟.相对而言,三维中心线的提取方式只有距离变换法、中轴变换法和腐蚀细化算法.
距离变换法[10]是指根据不同目的,将物体的体素点进行距离标识.目前主流的方法是基于双距离场的方法[11]:首先对物体进行边界距离变换,得到体素到达边界的边界距离场DFB (distance from boundary);其次指定源点,进行源点距离变换,得到源距离场DFS (distance from source);最后通过边界距离场中局部最大值的筛选,配合源距离场进行骨架点的连接.中轴变换法[12]在二维上可以用最大内切圆盘的相关术语定义,而在三维上则表现为最大内切球中心的集合.其中圆盘中心到达边界的距离称为圆盘法线,一个目标内点的最大内切圆在边界上至少有两个切点,而每个对称点有两个或多个圆盘法线.腐蚀细化算法[13]的思想则更为朴素,根据物体欧拉特性[14]以及连通性的不变性,给出在删除后不影响原物体拓扑结构的简单点,并以此为依据均匀、对称地从不同方向对目标物体边缘上的简单点 (Simple Voxel, SV)[15]进行剥离,直至仅剩下单像素宽的体素集合,去除该集合中的伪骨架点后得到最终的骨架线.
以上方法各自均有不同的局限性和一些共同不足.距离变换法中,在构建双距离场时不仅因需要对各体素点以迭代的方式进行距离标记而导致高时耗,还因需要与目标物体同样大小的内存空间储存距离场而带来高内存消耗.同时,依据不同的欧氏距离定义建立的距离场会产生不同的候选中心点,直接影响骨架线结果的一致性[16],且候选中心点通常是不连续的,连接时会造成骨架线在曲率较大位置的离心偏移,难以保证居中性.中轴变换法中,由于中轴变换是理想的数学模型描述,主要基于数学的几何推理证明,从而导致使用机器语言进行实现的难度大、算法复杂度高,常见的模型有地表火模型[17],距离曲面脊线模型[18].以上两种方法存在共同的缺陷就是易受边缘噪声干扰,且难以保证骨架的连续性.腐蚀细化算法的不足在于需要不断地对边缘的简单点进行判断,现有的判断模型复杂度均不够理想,导致当目标物体体素点过多时,带来巨大的时耗.
2 改进的腐蚀细化方法考虑到基于距离场的算法对于边缘噪声的敏感性和内存的大量消耗,以及传统腐蚀细化算法中对边缘点反复判断的高复杂度,本文提出一种基于LUT的快速三维腐蚀细化算法.该方法保留了传统腐蚀细化算法的稳定性,以及结果中对目标物体拓扑结构和连通性的完好保留性,并通过使用LUT的思想简化细化过程,避免重复判断,显著提高了细化速度.该方法首先从原始数据中用区域增长的方式分割出支气管二值图像,建立腐蚀细化模型并建立LUT,然后查找LUT进行腐蚀细化,最后对细化的结果进行剪枝处理.
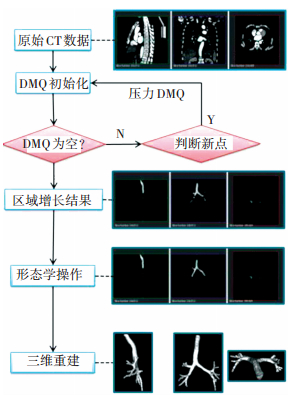
2.1 支气管二值数据的获取采用有监控的动态阈值区域生长配合形态学闭操作来获取组成支气管,流程及效果如图 1所示.首先以气管壁与空气CT值的差异为依据,通过应用DMQ (dynamic marking QUEUE) 的数据结构进行增长,提高了提取的速度.在顶层CT中选择气管入口作为增长原点压入DMQ,目标点离开DMQ时对其6邻域进行增长判断,若符合则压入DMQ.在判断目标点是否归入增长区域时,采用了18邻域平均值比较的方式,最大可能增加分割目标点数.对每一轮新增的点与上一轮增长结果进行比较,以进行溢出监控.
|
图 1 支气管分割流程 Figure 1 Process of airway segmentation |
该方法得到一个26连通的初步结果,为平滑边缘、填充管腔的空隙,在其基础上使用公式IMG ·M = (IMG ⊕ M) ⊕M进行形态学闭操作,用同一模版M分别对IMG进行膨胀腐蚀操作得到最终的二值分割结果.
2.2 细化方法细化过程具体分为4步:1) 腐蚀模型的建立;2) 基于腐蚀模型建立LUT (提高速度的关键步骤);3) 基于LUT进行快速细化;4) 对腐蚀结果进行剪枝处理.
2.2.1 腐蚀模型的建立在三维空间V3中,设中心点为c (x, y, z), 对于任意点p (i, j, k) 有如下的邻域定义:
| $\begin{array}{l} {\rm{N}}{{\rm{b}}_6}\left( p \right) = \left\{ {p\left( {i,j,k} \right) \in {\boldsymbol{V}^3}\left| {\left| {i - x} \right| + \left| {j - y} \right| - } \right.} \right.\\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {k - z} \right| = 1} \right\},\\ {\rm{N}}{{\rm{b}}_{26}}\left( p \right) = \left\{ {p\left( {i,j,k} \right) \in {\boldsymbol{V}^3}\left| {\left| {i - x} \right| < 2 \cap \left| {j - } \right.} \right.} \right.\\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. y \right| < 2 \cap \left| {k - z} \right| < 2} \right\},\\ {\rm{N}}{{\rm{b}}_{18}}\left( p \right) = \left\{ {p\left( {i,j,k} \right) \in {\boldsymbol{V}^3}\left| {\left| {i - x} \right| + \left| {j - y} \right| - } \right.} \right.\\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {k - z} \right| < 3} \right\} \cap {\rm{N}}{{\rm{b}}_{26}}\left( p \right). \end{array}$ |
将属于目标物体的体素定义为前景点Sfg,其余定义为背景点Sbg.在前景点集合中存在子集Ssub-fg,若其中所有元素均符合以下四种判断准则[19],则称之为简单点SV (simple voxel).
a) ∃ Sfg in Nb26 and Sum (Sfg in Nb26)>1;
b) ∃ Sbgin Nb6;
c) ∀ Sfg in Nb26 and is 26Connected (Sfg);
d) ∀ Sbg in Nb6 and is 6Connected By Nb18(Sbg).
a、b条件可以直接通过相应邻域中的前景点、背景点分布获得,而c、d条件的判断才是关键.
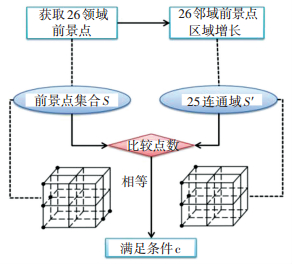
对于条件c,提出一种26邻域区域增长法,如图 2所示.根据条件c的描述易证明:若Nb26中的前景点可以彼此26连通,那么在该Nb26中,一定有且只有一个26连通的前景点区域.因此,取26邻域中的任意Sfg,在该Nb26中进行26邻域的前景点区域增长,得到增长结果集合S′.将其与26邻域中的前景点构成的集合S进行比较,若两者点数相同,则符合条件c.
|
图 2 条件c判断 Figure 2 Judgment of condition align="center" |
在条件d的判断上,并不能完全与条件c等同,因为在Nb18中的Sbg中,6连通的数量并不唯一.充分考虑到这一点,利用Nb18中Sbg的6邻域局部区域增长法,使用列表套列表的结构来储存连通的6邻域数组.在遍历结束后,将Nb6中的背景点集合S与连通的6邻域列表中的Si依次进行比较,得到是否可以删除.
2.2.2 邻域分布分析与LUT的建立分析腐蚀模型可以看出,判断一个前景点是否为简单点是由a、b、c、d这4个条件的满足情况决定的.进一步分析,条件a为非孤立点的判断,取决于Nb26;条件b为边界点的判断,取决于Nb6;条件c为Nb26的背景点的26连通情况,取决于Nb26;条件d为Nb26 前景点的18连通情况,同样取决于Nb26.因此可得出结论,对于任意体素点p,可根据其Nb26(p) 分布情况VC (voxel combination) 得到其简单性.
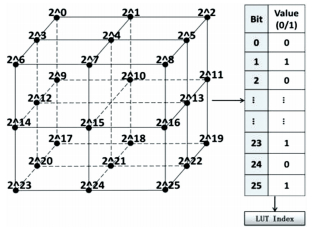
在二值图像前提下,任意体素点只有0或1两种取值.如图 3所示,若对26邻域指定排列顺序,则可等同于一个26bits的二进制数,进而任意一种VC将对应唯一的26bits二进制数,而相对的任意一个26bits二进制数也能唯一映射为一种VC.基于以上分析,可联想到建立LUT辅助腐蚀细化.在腐蚀细化过程中,将目标点的26邻域VC转化为26bits的索引,在LUT中进行查询判断.文献[20]显示LUT在二维的细化中得到了很好的应用,值得一提的是,由于三维计算量巨大,空间分布复杂性以及受拘束于过去计算机的内存,三维LUT鲜有人尝试.
|
图 3 26邻域转换 Figure 3 26 neighbors transition |
为避免建立LUT过程中的重复判断,对体素的邻域的空间分布状态进行特征分析.对于任意立方体,给出如下对于相似体素分布SVC (similar voxel combination) 的定义:
1) 通过任意旋转变换可以完全重合;
2) 通过左右手坐标系对换可以完全重合,即
| $\left| {\begin{array}{*{20}{c}} 1 &0&0&0\\ 0&{\cos \alpha }&{\sin \alpha }&0\\ 0&{ - \sin \alpha }&{\cos \alpha }&0\\ 0&0&0&1 \end{array}} \right|,$ | (1) |
| $\left| {\begin{array}{*{20}{c}} {\cos \beta }&0&{ - \sin \beta }&0\\ 0&1&0&0\\ {\sin \beta }&0&{\cos \beta }&0\\ 0&0&0&1 \end{array}} \right|,$ | (2) |
| $\left| {\begin{array}{*{20}{c}} {\cos \gamma }&{\sin \gamma }&0&0\\ { - \sin \gamma }&{\cos \gamma }&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right|.$ | (3) |
条件1) 可解释为依次以立方体每一面朝向的坐标系方向为观察方向,而后以该方向为轴向,使用如式 (1)~(3) 中对应方向的旋转矩阵对立方体进行围绕该轴向的三维旋转,为保证立方体空间位置不变,这里旋转的角度应该分别取0°、90°、180°、270°,这样通过旋转可得4*6共24种SVC;条件2) 可解释为条件1) 基础上的镜像变换,因此同样存在24种SVC.因此可得出结论,对于各向异性的立方体,存在24+24共48种SVC,应用在二值化的Nb26情况下,粗略估算在全空间2^26中存在2^26/48约为1398101种SVC.
| $\sum\limits_{i = 0}^{12} {2 \times \left( {C_{26}^i - R\left( i \right)} \right) + \left( {C_{26}^{13} - R\left( {13} \right)} \right).} $ | (4) |
而在二值化的Nb26情况下,并非所有分布都是各向异性,存在着大量的自反对称,经过式 (4) 的计算,其中i表示Nb26中前景点的个数,R(i) 表示Nb26中重复的组合个数,由于二值互补性,因此只需计算13次 (0~12个前景点的情况),外加13个前景点的情况.针对i取值不同时需要具体列出对称情况进行计算,但由于其复杂的旋转对称性,需要使用计算机辅助逻辑进行计算,最终得到不同前景点个数下SVC如表 1所示,SVC一共有1426 144种,并在实际运算遍历中加以检验.
| 表 1 26邻域中前景体素点与SVC关系表 Table 1 SVC of different fore-ground voxel in 26-neighbors |
基于以上分析,本文提出多线程并行配合双布尔数组的算法建立LUT,数组大小为2^26,下标代表该索引值所唯一对应的VC.其中一个数组为LUT,是后续腐蚀细化中所依赖的参照,其取值表示该VC下的中心点是否为简单点;另一个数组为MT (marking table),其取值用来表示该VC是否已被计算.将所有2^26个索引等分为多个索引段,平均分配给多个子线程,配合多核CPU进行计算,以达到最高的计算效率.
所有子线程将共享LUT和MT,每个子线程将同时并行遍历被分配的索引段.在具体计算索引时,每一次简单点判断的成本很高,但应用双数组算法可有效避免重复计算.对于一个索引值,首先在MT中查找判断该索引值是否已被计算,若尚未计算,则将该索引值转换为其对应的VC,并根据前文的判断条件和方法得出其是否为简单点;而后通过正方体的旋转对称性,获取该VC的所有其他47个SVC,并转换为索引序列IA (index array);最后在LUT中将IA中的索引值赋予与该VC相同的简单性,同时在MT中将IA中的这些索引值标记为已判断.双数组的优势也在此,通过标记MT避免了遍历到SVC所对应索引值时潜在的重复简单性判断,从而大大减少了判断的次数,整体加速了LUT的建立过程.为更为直观,下面给出该流程框架的伪代码.
函数1: CreateLUT (创建LUT的主函数)
输入:需要的线程数目threadNumber.
输出:计算好的lutArray.
for each i in threadNumber do
subThreads i = start_new_thread (MultiThreadCalculate (lutArray, mtArray, range i))
end for
wait_sub_threads (subThreads)
write_to_bin_file (lutArray)
函数2: MultiThreadCalCulate (用于计算指定区段的子函数)
输入:公共使用的lutArray,用于标记是否计算过的mtArray,需要遍历的区段range.
输出:计算指定区段range后的lutArray,标记指定区段range后的mtArray
for each i in Range
if not mtArrayi then
isSimple = isSimplePoint (i)
similarIndexArray = getSimilarIndex (i)
for each j in similarIndexArray
lutArrayj = isSimple
mtArrayj = true
end for
end if
end for
2.2.3 基于LUT进行迭代腐蚀细化在建立好LUT的基础上,传统的腐蚀细化过程便得以优化,其中对于SV的判断可以直接依据LUT的结果,而不是重新对前文4个定义条件的判断.在进行细化前先将图像中的前景点存入临时数组PointListfg,以避免重复遍历,提高效率.而后进行如下操作:
1) 在PointListfg中根据Nb26体素分布情况寻找边缘点,得到PointListborder.
2) 遍历PointListborder中的点,将Nb26体素分布转换为26 bits索引值,根据LUT的判断值进行简单点的判断删除.
3) 重复步骤1)、2) 直至PointListborder中再也无法找到简单点为止.
2.2.4 后续剪枝处理实验证实,通过上述腐蚀细化算法所得结果会在一些较粗的主气管上出现一些额外的毛刺,这无疑会对后续的内窥镜路径的规划带来不必要的分枝,需要进行剪枝处理.
根据毛刺分支长度短的特点,设计了一种尺寸自适应的剪枝算法.记当前的前景点集合为S,首先根据骨架线的体素数设置适当的剪枝阈值Threshold,设阈值百分比为th%,这里th取经验值1.7,因此经计算得到Threshold=S×th%.接着遍历细化后的骨架线,得到所有端点PointListend,以PointListend中的点为起点进行遍历,直至分支点,若其长度小于Threshold则将该支删除.
3 实验结果 3.1 实验环境与实验数据实验数据采用从上海肺科医院获得的5组肺CT图像序列,每组序列均包含有最少265层到最多468层CT断层图像,每层图像的分辨率均是512*512且灰度值在-2048到4196区间内.用于实验的PC CPU为Intel (R) Core (TM) i7-3610QM,RAM为6GB,OS为Win7 64-bit.算法的实现基于VTK v6.1.0开源库,配合QT在VS2008 IDE下进行开发和实验.
3.2 LUT的建立为获取最适合本实验环境的线程数量,以得到最快的LUT建立速度,以线程数作为输入参数进行实验,得到如图 4所示的结果.

|
图 4 LUT建立线程时间函数 Figure 4 Building LUT: threads number & time cost |
可见当线程数少于5个时,增加线程可显著减少用时,5个线程的处理过程表现最为优秀,当线程多于5个时,用时无明显减少.
3.3 骨架线提取结果与比较为比较基于LUT的方法与传统腐蚀细化算法的效率,采用如下的对比试验,使用相同的数据集进行重复试验100次,表 2列出了实验结果.
| 表 2 实验结果对比表 Table 2 Comparison of results with existing method |
在腐蚀细化阶段,基于LUT的平均时间为482.74 ms,而基于传统腐蚀细化算法的平均时间为11 077.7 ms,可见本文方法提高了22.95倍速度.
3.4 骨架线的提取效果图 5为本文算法提取骨架线的结果与基于距离变换算法[21]的结果,其中图 5(a)、(b)、(c) 三组结果中,上方为本文算法的结果,下方为距离变换算法的结果.通过对比可以看出,基于距离变换的方法会在末端发生断裂,不连续,在同一支气管段上可能产生多分支,不方便路径规划,且操作中需要手工选定端点,既不方便也无法保证连续性;而本文方法在支气管骨架线的提取上既可以保证骨架线在细末端的连续性,不发生断裂,也无需手动,具备可重复性.图 5中的三组数据显示,该算法很好地保持了支气管拓扑结果,同时也保障骨架线的中心性、连续性、一致性和可重复性,为内窥镜的漫游提供可能.

|
图 5 提取结果 Figure 5 Results of skeleton extraction |
本文同时还与基于距离场[21]算法得出的速度结果进行比较,由于使用不同的数据集,因此定义指标ts (thining speed) 来表示算法的效率作为比较依据,ts表示毫秒内处理的立方点数, 单位为103 voxels·ms-1.经计算,文献[21]的速度为220.16 ts,而本文的速度为45 253.39 ts,提高了205倍.结合本文与以上两种优化过的传统骨架线提取方式[21-22]的比较,可以充分看出基于LUT的算法能在保证骨架线拓扑结构完整的基础上,显著提高运行速度.
总的来说,基于LUT的算法在本质上优化了传统细化过程中的腐蚀细化环节,从而在整体上提高了骨架线提取的速度.不仅如此,LUT的另一大优势是将LUT的建立与LUT的参照分离,这样在简单点的定义发生变化时,可以直接更新LUT的数据,而不需要更改后续整个程序.
4.2 参数与复杂度分析基于LUT的腐蚀细化算法中,主要的输入参数体现于两点:一是LUT建立过程中线程数的选择,二是应用LUT进行腐蚀细化时,不同输入物体的体素数量.
在LUT建立过程中,线程数是重要的输入参数,并影响最终LUT建成的时耗.实验结果表明5个线程为最优,分析其原因为:当线程池大小为CPU数+1时,可达到最优利用率,即当执行密集型任务时既使偶尔因页缺失故障或者其他原因导致暂停时,此额外线程也可确保CPU的时钟周期不被浪费.实验PC为四核CPU,因此5个线程可达到最优化.算法的空间复杂度为2*2^26*1 byte = 128 MB,用于缓存双数组中的LUT和MT,在LUT建成结束后,得到的结果为一个64MB的二进制文件,可以直接作为查找腐蚀的依据.在时间上,对腐蚀细化的判断条件c的判断由于应用了26邻域内区域增长法,只用一重循环,是一个线性过程,将该步骤的时间复杂度降低为O(n);而对于条件d的判断,在区域增长上的平均时间复杂度依旧为O(n),而在列表比较上的平均时间复杂度为O(n2),两步之间为串行,因而整体的复杂度依旧为O(n2),但较传统方法相比依旧有所提升.
在腐蚀细化的过程中,由于LUT已经确立,因此主要的输入参数为物体的体素数.对3.3中的实验结果进行线性拟合,得到t=0.007 2v-152.91,拟合优度R2为0.988 5,其中t表示腐蚀细化的时耗,单位为ms,v表示物体的体素数.因此可得,腐蚀细化的时耗正比于输入物体的体素数.算法的空间复杂度取决于物体的体素数,会随着CT采集时分辨率的不同而有所变化,另外需考虑LUT占用的64 MB;在时间复杂度上,查询LUT接近于O(1),对体素点进行擦除的复杂度也为O(1),因此整体复杂度仍为O (1).
4.3 基于LUT算法的不足与基于其他理论的骨架线提取方式如距离变换法相比,基于LUT的腐蚀细化法不足在于最终得到的骨架线是组成骨架线的离散点,缺少点与点之间拓扑关系的描述,为后续骨架线拓扑结构分析带来了一定的困难.同时剪枝过程也有一定的局限性,无法精确区分细末较短的支气管与伪分支.而在LUT的使用中依旧可以作适当优化,如在查询表的尺寸上,若是对内存有苛刻的要求,可将LUT压缩为8MB,以bit的形式来储存每一个索引的索引值.由于对bit的检索需要额外的比较,其效率可能会有一定下降,这是一个棘手的问题.
受实验数据源限制,未进行大规模验证.同时受实验室硬件条件限制,缺少在其他配置相当的计算机上进行重复验证,也没有获取该算法在更差运行环境中的表现.更加充足的数据源和丰富的实验平台将能够对该算法有一个更全面的评估,这也是未来工作的目标.
5 结语基于LUT的腐蚀细化算法在传统的三维腐蚀细化算法中引入LUT的思想,通过邻域区域增长法优化了简单点腐蚀模型的判断,并通过二值化26邻域旋转对称性的分析进行快速的LUT建立,在腐蚀细化中使用LUT取代传统算法中对简单点的复杂重复判断过程,从而显著提高了骨架线的提取速度.实验结果表明:本文方法在速度上是传统细化法方法[22]的22.95倍,传统距离场方法[21]的近220倍,可以完好地保留肺部气管树的拓扑结构,具备易操作性、连续性和可重复性,为内窥镜浏览导航提供可能.
| [1] | CHEN W, ZHENG R, ZENG H, et al. Annual report on status of cancer in China, 2011[J]. Chinese Journal of Cancer Research, 2015, 27(1): 2. |
| [2] |
韦春晖. 肺癌早期诊断进展[J].
临床肺科杂志, 2010, 15(8): 1136-1138.
WEI Chunhui. Progress in early diagnosis of lung cancer[J]. Journal of Clinical Pulmonary Medicine, 2010, 15(8): 1136-1138. |
| [3] | JUNG S Y, PAE S Y, CHUNG S M, et al. Three-dimensional CT with virtual bronchoscopy: a useful modality for bronchial foreign bodies in pediatric patients[J]. European Archives of Oto-Rhino-Laryngology, 2012, 269(1): 223-228. DOI: 10.1007/s00405-011-1567-1 |
| [4] | WERNER H, SANTOS J R L D, FONTES R, et al. Virtual bronchoscopy for evaluating cervical tumors of the fetus[J]. Ultrasound in Obstetrics & Gynecology, 2013, 41(1): 90-94. |
| [5] | DE WEVER W, VANDECAVEYE V, LANCIOTTI S, et al. Multidetector CT-generated virtual bronchoscopy: an illustrated review of the potential clinical indications[J]. European Respiratory Journal, 2004, 23(5): 776-782. DOI: 10.1183/09031936.04.00099804 |
| [6] | DENIZ A, HOFFMAN E A, GEOFFREY M L, et al. Segmentation and analysis of the human airway tree from three-dimensional X-ray CT images[J]. IEEE Transactions on Medical Imaging, 2003, 22(8): 940-50. DOI: 10.1109/TMI.2003.815905 |
| [7] | COLE A J, O'Hare J M, McMahon S J, et al. Investigating the potential impact of four-dimensional computed tomography (4DCT) on toxicity, outcomes and dose escalation for radical lung cancer radiotherapy[J]. Clinical Oncology, 2014, 26(3): 142-150. DOI: 10.1016/j.clon.2013.11.024 |
| [8] |
陈刚, 吕煊, 王志成, 等. 肺CT图像的血管骨架化方法[J].
计算机科学, 2013, 40(5): 274-278.
CHEN Gang, LV Xuan, WANG Zhicheng, et al. Vessel Skeletonization Method for Lung CT Images[J]. Computer Science, 2013, 40(5): 274-278. |
| [9] | ZHOU Y, TOGA A W. Efficient skeletonization of volumetric objects[J]. IEEE Transactions on Visualization & Computer Graphics, 1999, 5(3): 196-209. |
| [10] | WAN M, DACHILLE F, KAUFMAN A.Distance-field based skeletons for virtual navigation[C]//Proceedings of the Conference on Visualization'01.IEEE Computer Society, 2001: 239-246. |
| [11] | WANG S, WU J, WEI M, et al. Robust curve skeleton extraction for vascular structures[J]. Graphical Models, 2012, 74(4): 109-120. DOI: 10.1016/j.gmod.2012.03.008 |
| [12] |
潘鹏, 贺三维, 吴艳兰, 等. 曲边多边形中轴提取的新方法[J].
测绘学报, 2012, 41(2): 278-283.
PAN Peng, HE Sanwei, WU Yanlan, et al. A new method for extracting curved-polygon medial axis[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 278-283. |
| [13] | CHEN W, SUI L, XU Z, et al.Improved Zhang-Suen thinning algorithm in binary line drawing applications[C]//International Conference on Systems and Informatic.Yantai:IEEE, 2012: 1947-1950. |
| [14] | CHOI W P, LAM K M, SIU W C. Extraction of the Euclidean skeleton based on a connectivity criterion[J]. Pattern Recognition, 2003, 36(3): 721-729. DOI: 10.1016/S0031-3203(02)00098-5 |
| [15] | MICHEL C, GILLES B. New Characterizations of Simple Points in 2D, 3D, and 4D Discrete Spaces[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2008, 31(4): 637-648. |
| [16] | GENG H, YANG J, TAN W, et al.Fast 3D skeleton extraction of airways and applications to virtual bronchoscopy[C]//The 26th Chinese Control and Decision Conference (2014 CCDC).Changsha:IEEE, 2014: 3879-3884. |
| [17] | LIU L, CHAMBERS E W, LETSCHER D, et al. Extended grassfire transform on medial axes of 2D shapes[J]. Computer-Aided Design, 2011, 43(11): 1496-1505. DOI: 10.1016/j.cad.2011.09.002 |
| [18] | GOLDBERGERA L, AMARAL L A N, GLASS L, et al. Physiobank, physiotoolkit, and physionet components of a new research resource for complex physiologic signals[J]. Circulation, 2000, 101(23): e215-e220. DOI: 10.1161/01.CIR.101.23.e215 |
| [19] | PALAGYI K. A 3D fully parallel surface-thinning algorithm[J]. Theoretical Computer Science, 2008, 406(1-2): 119-135. DOI: 10.1016/j.tcs.2008.06.041 |
| [20] |
杨威, 郭科, 魏义坤. 一种有效的基于八邻域查表的指纹图像细化算法[J].
四川理工学院学报 (自然科学版), 2008, 21(2): 61-63.
YANG Wei, GUO Ke, WEI Yikun. An effective thinning algorithm for finger print based on 8-neighbors LUT[J]. Journal of Sichuan University of Science and Engineering (Natural Science Edition), 2008, 21(2): 61-63. |
| [21] | JIANG G, GU L.An automatic and fast centerline extraction algorithm for virtual colonoscopy[C]//27th Annual International Conference of the Engineering in Medicine and Biology Society.Shanghai:IEEE, 2005: 5149-5152. |
| [22] |
陈磊, 王胜军, 郑全录, 等. 基于CT图像的三维拓扑细化算法及其在心脏CAD中的应用[J].
计算机应用, 2007, 27(B06): 406-410.
CHEN Lei, WANG Shengjun, ZHENG Quanlu, et al. A 3D topological thinning algorithm based on CT image and its application in cardiac CAD[J]. Computer Application, 2007, 27(B06): 406-410. |
 2017, Vol. 49
2017, Vol. 49


