2. 中国科学院大学,北京 100039;
3. 西安邮电大学, 西安 710121
2. University of Chinese Academy of Sciences, Beijing 100039, China;
3. Xi'an University of Posts and Telecomunications, Xi'an 710121, China
随着科技的不断进步,目标智能检测算法作为视频监控、交通管理、医药检验以及工农业产品监管等高层应用系统的技术基础,应用范围日益广泛,其相关算法研究受到了国内外学者的广泛关注.目前,图像检测算法通常基于人工设计特征进行模式识别.该类特征提取方法场景适应能力弱,且需以深厚的理论知识和特征设计经验为基础进行设计,实现起来费时费力[1].深度学习算法具有自主学习抽象特征和概念的能力,可以根据数据信息提取底层特征和多层次、抽象化的高级特征[2-3],因而成为当前模式识别领域研究热点.深度卷积神经网络提取特征具有旋转、缩放和平移不变性,较深度信念网络架构和深度自编码器等深度模型来说,更适宜进行图像检测和识别.
近年来,国内外学者开展了大量基于深度卷积神经网络的目标识别算法研究,并已取得很多研究成果.欧阳万里等[4]提出UDN算法,该算法基于深度模型框架,联合处理目标特征提取、形变遮挡和分类问题;Ross等[5]提出基于兴趣区域的CNN特征提取算法,该算法通过视觉显著性提取兴趣区域,提升CNN提取特征的辨识能力;罗萍等[6]提出分类特征提取算法,该算法在传统的CNN结构中引入可切换的RBM层,并将目标分为整体和部件两类进行分布特征提取;张宁等[7]提出部件-CNN深度模型,该模型将部件算法和CNN特征提取算法进行融合,并采用分块图片训练方法提升CNN特征提取泛化能力;张阳等[8]提出融合深度模型,该模型将受限波兹曼机和BP神经网络结合起来组建深度学习网络;曾敏等[9]提出变结构深度模型,该模型将遮挡层和变形层引入深度架构,降低遮挡行人误检率.上述研究成果多以深度模型结构为关注要点,忽视了输入数据对网络结果的影响及网络训练算法对模型特征提取时间及提取特征辨识力的影响,且忽略了深度模型梯度弥散及早熟问题的研究.
就以上问题,本文构建基于深度卷积神经网络的目标检测框架,并在深入分析深度卷积神经网络误差传播过程的基础上,提出指数自适应弹性动量参数学习方法.仿真实验结果表明:与人工特征检测方法相比,本文方法可有效提升目标检测精度;与其他动量同源更新机制相比,本文方法收敛速度快、振荡小,且能显著改善检测准确率.
1 深度卷积神经网络结构设计深度卷积神经网络由单层卷积神经网络堆叠产生.卷积核尺寸选取、阈值参数设置、网络深度设计和输出层特征维数选取是深度卷积神经网络特征提取算法的4个重要问题.卷积核表述“视觉感受野”大小,卷积核过大,则提取特征超出卷积核可表达的特征范围;卷积核过小,则无法提取有效局部特征.阈值参数用于控制网络模型对特征子模式的反应程度.网络深度表述模型对复杂问题的非线性表达能力.网络层数越多,特征表达能力越强,但网络层数过多易导致过拟合及实时性差等问题.输出层特征维数决定了网络收敛的速度,当样本集有限时,输出层维度过低则无法保证特征的有效性,输出层维度过高会产生特征冗余.
除此之外,由于深度网络架构是根据输入图像自主进行特征提取的,因此深度模型的输入数据对最终特征提取的影响也是至关重要的[10].传统深度卷积神经网络模型直接将原始图像作为输入数据.这样的方式虽然可使深度模型获得全面的数据信息,但是会大幅降低网络收敛速度,并在一定程度上影响深度模型特征提取能力.因此,对输入图像进行预处理,用以提高特定模式分类问题收敛速度及分类精度是有必要的.
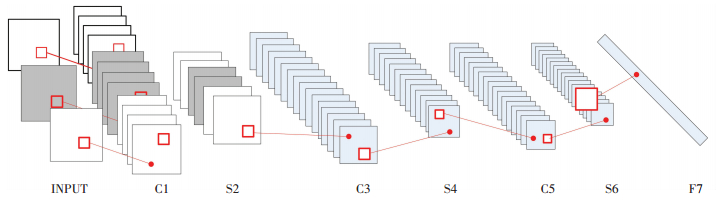
基于以上分析,本文针对行人检测识别问题,设计深度卷积神经网络模型,具体模型架构如图 1所示.
|
图 1 深度卷积神经网络模型 Figure 1 Deep convolutional neural network model |
基于卷积神经网络的目标检测深度模型共分为七层.输入图像在进行归一化、光照增强预处理后,计算其颜色特征及显著Centrist特征.以原始数据、颜色特征及显著Centrist特征三幅图像作为输入图像.网络中,第一层C1、第三层C3和第五层C5为卷积层,实现从低级到高级的特征提取;第二层S2、第四层S4和第六层S6是下采样层,用于特征降维;第七层F7为输出层,通过全连接方式提取最终抽象特征.该模型利用线性SVM对特征进行模式分类.为了提取具有更佳区分性能的特征,卷积层滤波器大小分别设为9×9、5×5和3×3,下采样层均采用形变最大下采样方法进行采样,激发函数采用LRel函数,输出层为全连接层.
2 基于非监督训练的初始化方法传统卷积神经网络通常采用随机初始化、非监督训练初始化等方法初始化模型参数.随机初始化方法易导致模型收敛时间增加、权值更新梯度消失、非最小值收敛等问题.非监督训练初始化方法多采用非监督深度网络预训练方式获取,该方法复杂度高、训练时间长.为克服以上问题,本文提出采用主成分分析法 (PCA) 初始化深度模型参数方法. PCA算法与受限自编码神经网络学习方式具有高度的相似性[11-12],因此可通过对原始数据进行主成分分析获得的特征向量来近似代替受限自编码器训练结果,用其作为深度卷积神经网络的初始化参数.并且,为了避免主成分分析算法降低深度模型泛化能力,初始化时的输入数据集均为经过图像特征检索扩充法和数据增强算法处理后的样本集.
本文方法属于非监督算法,可简单快速地获取较好的初始化参数,具体算法流程如下.
输入:N幅大小为m×n的图像数据集{Ii}N,滤波器大小k1×k2.
输出:滤波器组初始化权值wl1.
Step 1 预处理.仿射变换和归一化处理,获得标准图像样本集{Ii}i=1N, Ii∈ R m×n.
Step 2 获取滤波器取片样本集矩阵.
1) 在Ii中按k1×k2无重叠分块,获得 (m-k1+1)(n-k2+1) 个取片图像.
2) 栅格化取片图像为向量形式{xi}, xi∈ R k1k2×1.
3) 获得取片样本集矩阵,并去平均后,得
| $\mathit{\boldsymbol{X = }}\left[ {{{\bar X}_1},{{\bar X}_2}, \cdots ,{{\bar X}_N}} \right],\mathit{\boldsymbol{X}} \in {{\bf{R}}^{{k_1}{k_2} \times \left( {m - {k_1} + 1} \right)\left( {m - {k_2} + 1} \right)N}}.$ |
Step 3 求解矩阵X的主成分特征向量.
计算最小重构误差
Step 4 将向量重构为k1×k2大小矩阵,获得滤波器组初始化权值wl1:
| ${w^1} = {\rm{foma}}{{\rm{t}}_{{k_1}{k_2}}}\left( \boldsymbol{V} \right),w_l^1 \in {k_1} \times {k_2}.$ |
误差传递通过前向传播和反向梯度下降两步生成和调整权值.梯度下降法更新权值方法如式 (1) 所示,偏置更新方法如式 (2) 所示[13]:
| $w_{{\rm{new}}}^l = w_{{\rm{old}}}^l + \eta \left( { - \frac{{\partial E}}{{\partial w_{{\rm{old}}}^l}}} \right),$ | (1) |
| $b_{{\rm{new}}}^l = b_{{\rm{old}}}^l + \eta \left( { - \frac{{\partial E}}{{\partial b_{{\rm{old}}}^l}}} \right).$ | (2) |
式中:η为学习率;
由式 (1)、(2) 可知,要想实现权值和偏置寻优,首先必须获得误差对权值的梯度及误差对偏置的梯度.
1) 卷积层误差传播.对卷积层来说,其输出如式 (3) 所示为
| $x_j^l = f\left( {\sum\limits_{i \in {M_j}} {{M_j}*K_{ij}^l + {b_j}} } \right).$ | (3) |
式中:bj为第j种特征图的偏置,Mj为输入特征图分块,Kijl为卷积核.
根据敏感度函数求导公式可知,卷积层敏感度可由式 (4) 表示为
| $\delta _j^l = \beta _j^{l + 1}{\rm{up}}{\left( {\delta _j^{l + 1}} \right)^ \circ }{f^l}\left( {{u^l}} \right).$ | (4) |
式中:βjl+1为l+1层采样层卷积核,up代表上采样,δjl+1为δjl的1/4,°符号代表对应元素相乘.
由式 (4) 可推导获得卷积层误差对偏置的梯度如式 (5) 所示为
| $\frac{{\partial E}}{{\partial b_{{\rm{old}}}^l}} = \frac{{\partial E}}{{\partial {b_j}}} = \sum\limits_{\left( {u,v} \right)} {{{\left( {\sigma _j^l} \right)}_{uv}}} ,$ | (5) |
式中 (u, v) 为灵敏度矩阵的元素位置.
卷积层误差对权值的梯度,如式 (6) 所示为
| $\frac{{\partial E}}{{\partial w_{{\rm{old}}}^l}} = \frac{{\partial E}}{{\partial K_{ij}^l}} = \sum\limits_{\left( {u,v} \right)} {{{\left( {\delta _j^l} \right)}_{uv}}{{\left( {p_i^{l - 1}} \right)}_{uv}},} $ | (6) |
式中pil-1是xil-1与卷积核Kij卷积的块,(u, v) 为块中元素的位置.将式 (5)、(6) 带入式 (1)、(2) 即可获得卷积层的权值更新数值.
2) 采样层误差传播.采样层神经网络的输出可由式 (7) 表示为
| $x_j^l = f\left( {\beta _j^l{\rm{down}}\left( {x_j^{l - 1}} \right) + b_j^l} \right),$ | (7) |
式中βjl和bjl分别代表乘性偏置和加性偏置,一般设乘性偏置为1.
根据梯度下降敏感度公式,可知采样层敏感度如式 (8) 所示为
| $\delta _j^l = \delta _j^{l + 1}w_j^{l + 1 \circ }{f^l}\left( {{u^l}} \right).$ | (8) |
由此可得采样层偏置更新公式,如式 (9) 所示为
| $\frac{{\partial E}}{{\partial b_{{\rm{old}}}^l}} = \frac{{\partial E}}{{\partial {b_j}}} = \sum\limits_{\left( {u,v} \right)} {{{\left( {\delta _j^l} \right)}_{uv}},} $ | (9) |
将式 (9) 带入式 (2) 即可获得偏置值更新数值.
3.2 指数自适应弹性动量优化上述权值更新方法只是单一的层间传递梯度误差,没有考虑到上一时刻的梯度变化方向,即以前神经网络权值修正的经验.因此,在训练过程中常会出现过调和振荡现象,导致网络收敛缓慢.文献[14]提出采用动量方法可以加快收敛,文献[15]提出自适应动量梯度下降 (traingdx).但上述方法均未考虑上一时刻的梯度变化方向、动量方向以及当前误差对权值梯度方向的一致性.且动量因子没有促进收敛,提升学习性能能力.
本文采用误差对权值梯度的指数函数调整动量因子步伐,使其在误差平坦区时,动量因子增大,加快网络收敛速度;误差陡峭区时,减小动量因子,避免网络收敛过快,错过极小点出现的不稳定.并且,基于符号函数判别方法,促使动量因子在前后两次梯度方向相同时比例增大,在前后两次梯度方向相反时比例减小.动量因子更新公式如式 (10)、式 (11) 所示为
| $a = \exp \left( {{A_k}} \right){\rm{sign}}\left( {{D_k},\Delta {w^{k - 1}}} \right)\frac{{{D_k}}}{{{{\left\| {\Delta {w^{k - 1}}} \right\|}^2}}},$ | (10) |
| ${A_k} = - {\lambda _1}\left\| {{D_k}} \right\| - {\lambda _2}.$ | (11) |
式中:λ1和λ2为调节因子,满足λ1>0, λ2>0;
由式 (10) 可以看出,‖Dk‖增大,则a减小;‖Dk‖减小,则a增大.即误差曲面陡峭,动量因子减小;误差曲面平坦,动量因子增大.
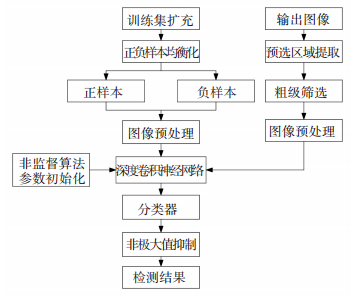
4 行人检测框架为了提升行人检测的实时性及准确度,受R-CNN目标检测算法思想的启发,根据模式识别分类框架设计粗细二级行人检测框架,如图 2所示.为提升深度卷积神经网络提取特征分类能力,采用图像特征检索扩充法和数据增强算法对样本集进行扩充.为了快速检测行人目标区域,采用二值梯度规范法和选择搜索法级联选取行人预选区域,并根据行人宽高比和头部梯度范围进一步缩小特征提取窗口数量.对需提取特征的窗口进行大小、亮度均衡预处理,输入深度模型提取特征.最后,通过线性SVM分类器进行分类,获得行人最终检测结果.
|
图 2 基于CNN的行人检测算法架构 Figure 2 Pedestrian detection algorithm based on CNN |
行人检测主流数据集有Caltech数据库、INRIA数据库等. Caltech数据库分辨率多样,具有多种远近行人样本;INRIA数据库背景复杂,具有光照变换和遮挡等情况.为使网络具有更强的适应能力,以Caltech数据集、INRIA数据集和现实场景数据集为基础,根据图像特征相似度检索扩充法以及数据增强法对训练集进行扩充,最终选择正样本12 316个,负样本162 000个作为样本集.将样本随机分为6组,正负样本均衡化后,前五组作为训练集,后一组作为测试集.
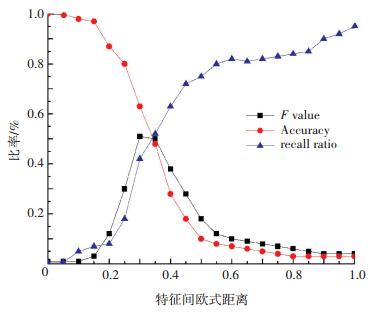
5.2 网络阈值选取准确率、召回率和F值是行人检测算法的主流评价指标.由于准确率与查全率之间有互逆性与相关性,因此,查全率低则准确率高,反之会低.为了使两者达到平衡,阈值选取至关重要.以行人作为研究对象,使用欧式距离作为度量方法,来观测各区间的曲线变化,通过实验确定阈值取值范围. 图 3为取不同阈值时,行人检测算法F值、查重率以及准确率之间的变化趋势图.由图 3可以看出,在阈值 < 0.3时,查全率相对较低,准确率相对较好,但与之相对应的F值却相对较低,而当阈值 > 0.5时,查重率相对较高,而准确率却有所下降,所以在阈值为[0.3, 0.5]之间,得到的F值较优.
|
图 3 行人查重率、准确率与阈值之间的关系 Figure 3 Relationship between the rate of recall rate, the accuracy rate and the threshold value |
为检测文中设计深度模型的有效性,将本文算法与经典行人检测算法HOG+SVM、HOF+CCS以及传统CNN检测方法进行比较,获得如图 4和表 1所示实验结果.由图 4和表 1结果可知,本文算法相对人工设计特征算法和传统深度卷积模型算法来说,漏检率、误检率更低,检测准确率更高.与传统深度卷积模型相比,算法检测速度提升20%以上.

|
图 4 检测算法结果比较 Figure 4 Comparison of detection algorithm results |
| 表 1 检测速率对比表 Table 1 Comparison of detection speed |
对手机拍摄校园内图书馆和教学楼前行人自然真实场景进行检测,效果如图 5所示.由图 5可见,本文算法可在行人尺寸适中,光照具有一定差异,存在垂直梯度干扰的情况下取得较好的检测效果.能检测出遮挡小于40%的行人,标示窗口与行人尺寸基本相符.

|
图 5 实际场景行人检测结果 Figure 5 Pedestrian detection results in real scene |
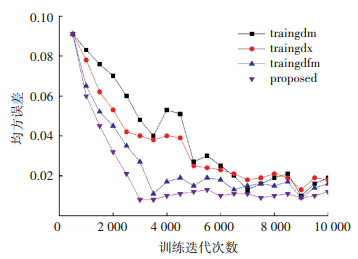
为评估本文所提指数弹性动量网络训练算法的有效性,将本文算法与标准动量 (taingdm)、自适应动量 (traingdx) 及弹性动量机制 (traingdfm) 算法比较,以收敛速度、收敛震荡性能、检测准确率作为评价指标,在上文所述数据集上获得结果如图 6和表 2所示.
|
图 6 动量算法收敛均方误差曲线对比 Figure 6 Convergence mean square error curve of momentum algorithm |
| 表 2 算法准确率对比表 Table 2 Comparison of momentum algorithm accuracy |
图 6为收敛均分误差曲线对比图,图中横坐标为训练轮数,纵坐标为均方误差.由图 6可见,本文算法与标准动量 (taingdm)、自适应动量 (traingdx) 算法及弹性动量机制 (traingdfm) 相比收敛速度更快,收敛曲线更平滑. 表 2为算法准确率对比表.由表 2可知,指数弹性动量算法在不同深度模型均可取得较好检测效果,准确率均有不同程度提高.提高幅度平均值分别为1.6%,1.8%和6.19%.
6 结论本文基于深度卷积网络构建目标检测识别框架,在分析深度架构误差传播基础上,提出指数自适应弹性动量的参数学习方法.仿真实验表明,本文方与同人工特征检测算法相比,检测精度高,漏检率低,与同源误差优化算法相比,收敛速度更快,收敛曲线更平滑.
| [1] |
刘操, 郑宏, 黎曦, 余典. 基于多通道融合HOG特征的全天候运动车辆检测方法[J].
武汉大学学报 (信息科学版), 2015, 40(8): 1048-1053.
LIU Cao, ZHENG Hong, LI Xi, et al. A method of moving vehicle detection in all-weather based on melted multi-channel HOG feature[J]. Journal of Wuhan University (Information Science Edition), 2015, 40(8): 1048-1053. |
| [2] | KULKARNI P, ZEPEDA J, JURIE F, et al. Hybrid multi-layer deep CNN/aggregator feature for image classification[C]// IEEE International Conference on Acoustics, Speech and Signal Processing.Brisbane: IEEE, 2015. |
| [3] | SCHMIDHUBER J. Deep learning in neural networks: an overview[J]. Neural Networks the Official Journal of the International Neural Network Society, 2015, 61: 85-117. DOI: 10.1016/j.neunet.2014.09.003 |
| [4] | OUYANG Wanli, WANG Xiao. Joint deep learning for pedestrian detection[C]// IEEE International Conference on Computer Vision.Sydney: IEEE Computer Society, 2013:2056-2063. |
| [5] | GIRSHICK R, DONAHUE J, DARRELL T, et al. Rich feature hierarchies for accurate object detection and semantic segmentation[C]//IEEE Conference on Computer Vision & Pattern Recognition. Columbus: IEEE, 2014:580-587. |
| [6] | LUO P, TIAN Y, WANG X, et al. Switchable deep network for pedestrian detection[C]// 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR).Columbus: IEEE Computer Society, 2014:899-906. |
| [7] | ZHANG N, PALURI M, RANZATO M, et al. PANDA: Pose aligned networks for deep attribute modeling [C]//IEEE Conference on Computer Vision & Pattern Recognition. Columbus: IEEE, 2014:1637-1644. |
| [8] |
张阳. 结合纹理特征和深度学习的行人检测算法[J].
辽宁工程技术大学学报 (自然科学版), 2016(2): 206-210.
ZHANG Yang. Pedestrian detection method of texture feature and deep learning[J]. Journal of Liaoning Technical University (Natural Science), 2016(2): 206-210. |
| [9] |
曾敏, 周益龙. 基于深度学习模型的行人检测研究与仿真[J].
南京邮电大学学报 (自然科学版), 2015, 35(6): 111-116.
ZEN Min, ZHOU Yilong. Simulation of pedestrian detection based on deep learning model[J]. Journal of Nanjing University of Posts and Telecommunications (Natural Science), 2015, 35(6): 111-116. |
| [10] | DONG C, CHEN C L, HE K, et al. Image super-resolution using deep convolutional networks[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2016, 38(2): 295-307. |
| [11] | BALDI P, HORNIK K. Neural networks and principal component analysis: learning from examples without local minima[J]. Neural Networks, 1989, 2(1): 53-58. DOI: 10.1016/0893-6080(89)90014-2 |
| [12] | CHAN Tsunghan, JIA Kui, GAO Shenghua, et al. PCANet: a simple deep learning baseline for image classification[OL]. http://arxiv.org/abs/1404.3606, 2014. |
| [13] | BHM Sadeghi. A BP-neural network predictor model for plastic injection molding[J]. Journal of Materials Processing Technology, 2000, 103(3): 411-416. DOI: 10.1016/S0924-0136(00)00498-2 |
| [14] |
MITCHELLT M, 曾华军, 张银奎.
机器学习[M]. 北京: 机械工业出版社, 2003.
MITCHELL T M, ZENG Huajun, ZHANG Yinkui. Machine learning[M]. Beijing: Machinery Industry Press, 2003. |
| [15] | AGRAWAL S S, YADAVA V. Modeling and prediction of material removal rate and surface roughness in surface-electrical discharge diamond grinding process[J]. Materials and Manufacturing Processes, 2013, 28(4): 381-389. DOI: 10.1080/10426914.2013.763678 |
 2017, Vol. 49
2017, Vol. 49


