在生产实践中，化工、核电、航空航天以及车辆、电器等行业的各种泵阀、发动机、工模具、电磁接触器等关键零部件经常因多碰而失效.使用这类零部件的大型企业，每年因多碰失效的直接损失不下数千万，失效后因检修、停产带来的间接经济损失更加巨大.这类零构件均是在远低于材料屈服极限的低应力多碰载荷作用下，发生永久性的宏观塑形累积变形现象.这种多碰工况碰撞速度一般在5~20 m/s，其应变率介于棘轮^[1-3]和强冲击^[4]之间.因此，其碰撞机制不同于棘轮，也不同于强冲击的研究.多冲碰撞研究范围涉到金属材料和高分子材料, 甚至到医学领域^[5-8].本课题组利用自制的凸轮-弹簧式碰撞试验系统针对低应力多碰载荷下的应变量及微观结构进行了大量研究^[9-10]，特别在超低应力 (约为屈服限的1/6~1/10) 多碰下材料的塑性性能方面进行了较深入的研究，发现了试样碰撞过程中的塑性变形量先变大后变小，总变形量随碰撞次数的增加而累积.碰撞次数达到一定值时，变形增量趋于零，累积应变趋于某一安定值.这一特性与材料典型的蠕变曲线中减速蠕变段十分近似，暂称之为“类蠕变”.它是材料的一种尚未受到足够关注的新的动态塑性力学现象.

从多碰“类蠕变”的特殊塑性变形行为可以推断：其本构关系远非一般的应力应变关系所能表达，很可能与碰撞功 (能)、碰撞速度等突加性的外在条件相关.本文注重低能量对金属材料多碰塑性行为的研究，为了避免过多干扰因素选取了YT01试样进行多碰试验，研究碰撞能对金属材料多碰塑性变形规律的影响.

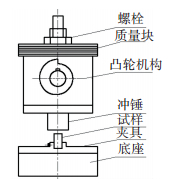
1 实验 1.1 实验设备

在实验室自制凸轮机械式多冲碰撞试验机^[11]上进行多碰实验，试验装置如图 1所示.低能量冲击加载方式采用质量块形式加载，在凸轮带动下冲锤在冲击前完全作自由落体运动.冲击的作用力由冲击行程和冲击质量引起，保证了稳定的冲击力.而碰撞能量由重力势能引起.冲击过程中的力与能量可以通过调整质量块和行程来实现.考虑到冲锤下落过程中能量的损失，采用压力传感器检测冲击力的大小.

1.2 碰撞能量建模及试验参数设置

为简化模型，设定冲锤在凸轮的作用下做自由落体运动，冲锤的势能完全转化为动能.假设第一组冲击参数为：冲击力为F₁, 冲击能量为W₁，冲击行程为h₁，冲锤整体质量为M₁, 冲击速度为v₁，冲击后速度为0，冲击时间为Δt.第二组冲击参数为：冲击力为F₂，冲击能量为W₂，冲锤整体质量为M₂，冲击前速度为v₂，冲击后速度为0，冲击时间为Δt.

设定两组冲击状态冲击力相同，冲击能量相差K倍，可得

$\left\{ \begin{array}{l} {F_1} = {F_2}, \\ {W_1} = K{W_2}. \end{array} \right.$

(1)

假定冲锤在凸轮的作用下势能完全转为为动能，根据能量守恒定律，冲击前冲锤的动能为

$\left\{ \begin{array}{l} {M_1}g{h_1} = \frac{1}{2}{m_1}v_1^2, \\ {M_2}g{h_2}{\rm{ = }}\frac{1}{2}{M_2}v_2^2. \end{array} \right.$

(2)

对冲锤来讲，受到样品的反作用力F，由于冲力的瞬时值较难确定故简化为平均值，则

$\left\{ \begin{array}{l} {{\bar F}_1}\Delta {t_1} =-{M_1}{v_1}, \\ {{\bar F}_2}\Delta {t_2} =-{M_1}{v_2}. \end{array} \right.$

(3)

依据实验室前期大量试验得知Δt₁≈Δt₂，合并式 (1)~(3) 计算可得

$\left\{ \begin{array}{l} \frac{{{h_1}}}{{{h_2}}} = {k^2}, \\ \frac{{{M_1}}}{{{M_2}}} = \frac{1}{k}. \end{array} \right.$

(4)

由此可以看出，在相同冲击力作用下，获得不同冲击能量，需要同时调节冲锤质量和冲击行程.即在相同的冲击应力下，冲击能量变为K倍，需要将冲击行程调节为原行程的$\frac{1}{{{k^2}}}$，冲锤质量调节为原质量K倍.

因此，多冲碰撞试验参数设置如下.冲击力采用压力传感器测试得到，根据应力计算公式$\sigma = \frac{F}{A}$，计算冲击时峰值冲击应力.冲锤质量砝码已知，根据式 (4) 可得到不同的试验参数.在实验室多冲碰撞疲劳试验机上进行多碰试验，碰撞次数从2×10³，4×10³，8×10³，16×10³，…按几何级数递增，最终终止次数为256×10³, 碰撞频率为4 Hz.多碰试验样本参数如表 1所示.

1.3 试样制备

为避免干扰因素，试样选用工业纯铁YT01，切割尺寸为7 mm×9 mm×42 mm，其力学性能如表 2所示，试样网格形貌如图 2所示.

1.4 试验方法

采用坐标网格法^[10]计算冲击碰撞后试样的塑性变形量.基于课题组前期研究，低应力多碰载荷下，试样的变形呈“趋表效应”.因此，在试样7 mm×42 mm面距冲击表面10 mm距离内划分0.5 mm×0.5 mm网格，每隔2 000, 4 000, 8 000，……利用用XTL-1体视显微镜拍摄网格图片，并测量网格变形量，使用JX68302-00工具显微镜及冷场扫描电镜 (SEM-S-570) 观察多碰前后试样的微观组织结构.

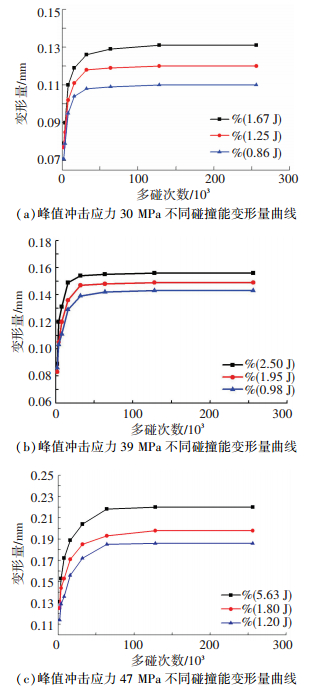
2 结果与分析 2.1 试验结果

试样在不同冲击碰撞能下，经过碰撞次数为2 000、4 000、8 000、…、256 000次后，试样多碰后累积变形量与冲击次数之间的关系曲线如图 3所示.

图 3可以看出，试样在相同的峰值冲击应力、不同的冲击碰撞能下，多碰后试样累积变形量不同.冲击碰撞能量越大，累积变形量越大.多碰次数在16 000次以下，随着冲击次数的增加，试样累积变形量不断增加.当多碰次数超过16 000次后，试样变形量增量趋于平缓，64 000次后，变形量趋于安定.不同的峰值冲击应力，试样的塑性变形量也不同.峰值冲击应力为30 MPa，碰撞能1.67 J，多冲碰撞2 000次后，累积塑性变形量为0.079 mm；峰值冲击应力为39 MPa，碰撞能2.5 J，多冲碰撞次数为2 000次，塑性变形量为0.089 mm；冲击应力为47 MPa，碰撞能5.63 J，多冲碰撞次数为2 000次，试样的塑性变形量为0.131 mm.结果表明，相同的多冲碰撞次数，随着峰值冲击应力的增大，试样累积塑性变形量也变大.

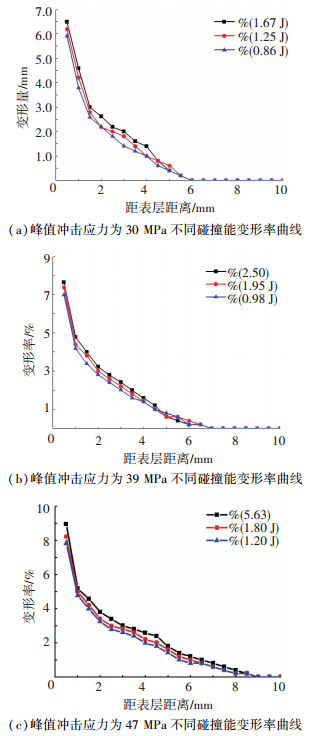
不同冲击能量下，变形率与冲击接触表面距离的关系和图 4所示.从图 4可看出，在相同峰值冲击应力下，试样的变形率与冲击碰撞能量有关.冲击碰撞能量越小，试样变形率越小.距冲击表面距离越小，试样的变形率越大，距冲击表面距离越大，试样变形率变化趋于平缓，当达到一定距离后，变形率为0.冲击应力为30 MPa，距表面6 mm时，变形率为0；冲击应力为39 MPa，距表面为7 mm时，变形率为0；冲击应力为47 MPa，距表面距离为8.5 mm时，变形率为0.三组试验表明，多碰后塑性变形终止于距表面6~9 mm处.在不同的峰值冲击应力作用下，表层的变形率变化也不相同.冲击应力为30 MPa，表层的最大变形率为6.49%；冲击应力为39 MPa，表层的最大变形率为7.65%；冲击应力为47 MPa，表层的最大变形率为8.95%.

实验结果表明：峰值冲击应力一定时，多冲碰撞能越大，试样变形率越大.当距冲击表面一定距离后，试样变形率趋近于0.而峰值冲击应力影响试样变形终止的位置，峰值冲击应力越小，试样变形终止的位置距冲击表层距离越小; 峰值冲击应力越大，试样变形终止位置距表层距离越大.

图 5为多冲碰撞后，在试样侧面距冲击表层1 mm内的微观组织结构图.拍摄前曾以4%的硝酸酒精腐蚀试样. 图 5(a)为纯铁多冲碰撞前微观组织结构，主要为铁素体与珠光体的混合组织，珠光体所占比例较小，铁素体晶粒为沿加载方向呈长条状的非等轴晶.由图 5(b)可以看出，多冲击碰撞后纯铁试样距冲击表层2 mm处的显微组织可观察到明显的穿晶裂纹及孔洞.穿晶裂纹扩展方向基本与加载方向平行，且大致在同一竖直方向上的相邻裂纹与孔洞有相互扩展连接形成更大裂纹的趋势，说明在多冲碰撞工况下，金属材料内部局部区域内存在强烈的剪切变形^[12]. 图 5(c)、(d)分别为冲击应力39 MPa，冲击能量为2.6、0.98 J多碰后的微观组织结构，可以看出，多次冲击加载后部分铁素体晶粒沿加载方向被压缩，且有晶粒碎化形成亚晶粒的情况，多冲碰撞能越大，微观组织越细化. 图 5(e)、(f)分别为冲击应力30 MPa, 0.86 J，30 MPa, 5.63 J多碰后的金相显微组织结构，其中冲击能量为5.63 J的微观组织结构明显细化.通过对多碰前后微观组织结构对比发现，试样在经过低应力小能量多冲碰撞后，晶粒形状发生了变化.试样多碰后，原始的非等轴晶粒逐渐伸长，亚晶粒尺寸变小，晶粒界增加.

为了进一步研究YT01试样微观机理，对YT01样本进行了多碰前后X射线单晶衍射试验并进行数据分析，YT01试样在峰值冲击应力39 MPa，碰撞能量分别为2.6 J、1.95 J、0.98 J的试验条件下亚晶尺寸如表 3所示.

多冲碰撞前，YT01试样的亚晶尺寸为33.7 nm，多冲碰撞后，亚晶尺寸变小.多冲碰撞能为2.6 J时，亚晶尺寸为27.1 nm, 多冲碰撞能为1.95 J时，亚晶尺寸为28.8 nm，多碰碰撞能为0.98 J时，亚晶尺寸为29.8 nm.可以看出，随着多冲碰撞能的增大，亚晶尺寸减小, 微观组织细化.低应力多碰动态冲击不同于准静态加载时金属的塑性变形，冲击波使金属在总的宏观应变很小时就可诱发高密度的位错^[13].而低应力循环碰撞，可能导致试样微观组织结构出现位错与亚晶^[14]，从而导致微观组织细化.

2.2 结果分析

1) 试样在峰值冲击应力仅为屈服强度的1/4~1/3时，经过多次冲击碰撞后，在距表面10 mm以内竟发生了高达6.49%-8.95%的塑性变形. Lensky分析了有限长度杆撞击刚性墙的结果，很好地解释了塑性区只在局部出现的原因.根据运动相对性原理，低应力多碰可认为冲头撞击试样. Lensky^[15]认为，当材料的碰撞速度超过材料的屈服速度时，试样发生永久的塑性变形.试样YT01的屈服速度为4 m/s (${\upsilon _Y} \equiv \frac{Y}{{{\rho _0}{c_0}}} = \frac{Y}{{\sqrt {E{\rho _0}} }} = 4{\rm{m/s}}$)，低应力多碰速度为8~20 m/s，在低应力多冲碰撞中碰撞速度大于材料屈服速度，试样材料发生了塑性变形.由于弹性速度${c_0} > {c_p}\left( {{c_0} = \sqrt {E/{\rho _0}} = 3.2 \times {{10}^3}{\rm{m/s}}} \right)$，塑性区变形区小于试样长度，不管碰撞速度有多高，塑性区区域不可能遍及整个试样，塑性残余应变永远只存在于局部区域.而塑性变形具有累积效应，256 000次多碰后试样局部区域变形量增大，且不会超过试样长度.这与试验结果相符，塑性变形区域呈现“趋表效应”，且存在于距表层的10个毫米以内，而不是遍及整个试样.

2) 在同样峰值冲击应力下，碰撞能量越大，塑性变形量越大.根据能量吸收一般原理中不可逆能量转换原则^[16], 结构和材料能将大部分的输入动能通过塑性变形或其他耗散过程转换为非弹性能，而不是以弹性能形式将之储存. YT01是韧性材料，韧性材料吸收能量最有效的机制为塑性变形.因此，试样在相同冲击应力下，碰撞能量越大，材料的塑性变形量也越大.

3) 由图 2和图 3交叉来看，即使碰撞能较大，若峰值冲击应力较小，材料变形量也较小；反之即使碰撞能较小，但峰值冲击应力较大，材料变形也会比较大.在多碰冲击过程中，峰值冲击应力对多碰后试样变形的影响要比碰撞能明显.这是因为在实验过程中，冲击能量只有一部分被试样吸收，而峰值应力则不存在这种情况.

设F为峰值冲击力，σ为峰值冲击应力，W为冲击碰撞能，A为冲击接触面积，t为冲击时间，v为冲头接触试样时的速度，则有

$Ft = mv, $

(5)

$F = \sigma A, $

(6)

$W = \frac{1}{2}m{v^2}.$

(7)

联立式 (5)~(7)，可得

$\sigma = \frac{2}{{Avt}}W, $

而实际实验中，则是

$\sigma = \frac{2}{{Avt}}\left( {W \cdot \eta } \right).$

4) 试样在低应力多次冲击碰撞后，显微组织发生了明显的变化.在冲击碰撞过程中，材料微观组织结构出现晶粒细化，晶粒界增多.根据霍尔-配奇方程${\sigma _{ys}} = {\sigma _0} + \frac{{k'}}{{\sqrt d }}$(σ₀和k′为材料常数)^[14]，由于晶粒细化，平均晶粒尺寸d变小，材料屈服应力变大，即材料屈服应力随着晶粒尺寸的减小而增大.因此，材料在256 000次多碰后，材料的塑性变形终止，变形率曲线斜率为0.

5) 试样在多碰后，距表面2 mm处出现穿晶裂纹和孔洞.试样中出现穿晶裂纹，穿晶裂纹扩展方向与加载方向平行，且大致在同一竖直方向上的相临裂纹与孔洞有相互扩展连接形成更大裂纹的趋势，由此纯铁试样中晶体的穿晶断裂属于微孔聚集型剪切断裂，说明在低应力多冲碰撞工况下，金属内部局部区域内存在着强烈的剪切变形.试样中出现的孔洞，主要是因为钢铁试样中存在硫化锰等夹杂物，夹杂物与基体连接较弱，易在连接处产生应力集中，随着冲击碰撞的反复进行，当应力集中达到一定程度后在连接处开裂形成孔洞.因为在低应力多碰撞过程中沿加载方向存在剪切变形，孔洞随着基体的塑性流动而长大形成裂纹，且和滑移方向上的孔洞、裂纹相互汇合，曲折向前发展.

3 结论

1) 在峰值冲击应力仅为静屈服应力的1/4~1/3时，YT01经过多次碰撞后发生了明显的塑性变形，距表层6~9 mm内，发生了6%~8%，多冲碰撞能越大，累积变形量越大.随着多碰次数的增加，试样累积塑性变形量增加，经过一定多碰冲击次数后，塑性变形趋势安定，256 000次多碰后，塑性变形终止.因此，在低应力多冲碰撞中，材料的塑性变形与峰值冲击应力有关，也与多碰次数有关.

2) 相同峰值冲击应力和不同碰撞能量工况下，试样累积塑性变形量也不同.多冲碰撞能量越小，试样的塑性累积变形量越小，多碰冲击碰撞能量越大，试样累积塑性变形量越大.因此，试样累积塑性变形不仅与峰值冲击应力有关，也与多冲碰撞能相关.由于在多冲碰撞过程中，能量传输过程中有一定的损耗，因此，多冲碰撞能量对试样变形的影响小于峰值冲击应力.

3) 试样在低能量多冲碰撞中，碰撞前后材料显微组织结构发生了明显变化，原始的非等轴晶粒多碰后被拉长.低应力、低能量循环冲击，试样微观组织的亚晶粒尺寸变小，亚晶粒增加.由于位错和亚晶的出现导致材料屈服应力提高, 因此最终在25 000次多碰后，材料变形终止在距表层一定距离内, 即低能量多冲碰撞引起的塑性变形具有“趋表效应”.碰撞初期的塑性变形只发生在碰撞面的表层，随着碰撞次数的增加，表层累积塑性变形加大，同时第二层开始变形；继续碰撞，第一、二层的累积塑性变形继续加大，同时第三层开始变形，以此由表及里传递.