2. 结构工程灾变与控制教育部重点实验室 (哈尔滨工业大学),哈尔滨 150090
2. Key Lab of Structures Dynamic Behavior and Control (Harbin Institute of Technology), Ministry of Education, Harbin 150090, China
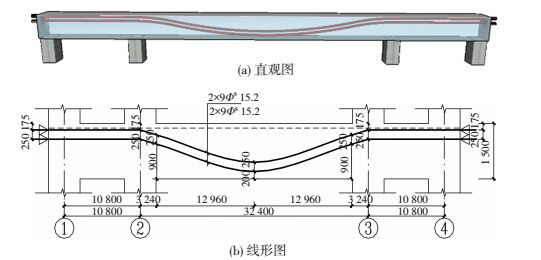
大型商场和室内游泳池等公共建筑,常因使用需要,采用内跨较大而与其相邻的两边跨跨度相对不大的大内跨小边跨预应力混凝土框架结构.以往该类框架梁内布置预应力筋时,常基于定性上实现大跨梁的各控制截面正截面承载能力最大原则,将大跨所需的预应力筋布置为连续曲线,并在与其相邻的两小跨按水平直线延伸至边柱,典型布筋方式见图 1(线形1).工程实践中已按这种预应力筋布置方式设计建造了大量预应力混凝土结构,较好满足了结构的安全性和适用性要求,然而,该种布筋方式也存在未按荷载平衡思路实现小跨内所需均匀分布竖向向上的预应力等效荷载问题.
|
图 1 按线形1布置预应力筋 (mm) Figure 1 Prestressing tendons arranged as profile 1(mm) |
考虑到实际工程中框架结构,与大跨相邻的小跨跨度通常不大于大跨跨度的1/3,若将大小跨 (2小跨+1大跨) 统一按一跨考虑,取为三段连续正反抛物线的线形布置预应力筋 (线形2),张拉引起的竖直向上的预应力筋等效荷载不但可较好平衡作用在大跨内的竖向外荷载,而且还能有效平衡小跨内的竖向外荷载.按照张拉预应力筋产生的等效荷载平衡竖向外荷载的设计思路,这种预应力筋线形更为优化.然而,这种线形也可能使大跨支座控制截面预应力筋合力点距其受拉边距离变大,从正截面承载力分析角度,减小了预应力筋有效高度,降低了预应力筋抗力的内力臂,不利于该截面正截面承载力.事实上,在张拉按该种线形布置的预应力等效荷载作用下,大、小跨相邻控制截面将产生一定量值的与外载弯矩相反的次弯矩.从而,减小了该控制截面外载弯矩设计值与次弯矩之和,非预应力筋布筋适当的条件下,该控制截面也易于满足正截面承载力要求.以一典型工程为例,对比分析了两类线形条件下张拉引起的预应力等效荷载及其作用下的综合弯矩、主弯矩和次弯矩,分析了相同条件下竖向荷载标准值与预应力等效荷载共同作用下控制截面拉区边缘应力及压区边缘应力分布的异同,验算了正截面承载力,验证了若将大跨及相邻的两小跨统一考虑将预应力筋按三段连续正反抛物线布置,不但可有效平衡大跨内竖向外荷载而且也可平衡小跨内的竖向外荷载设想的合理性.
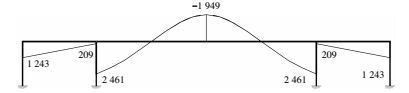
1 常规线形 (线形1) 的分析设图 1所示的预应力混凝土梁考虑全部预应力损失后的有效预应力为1 000 N/mm2,则张拉图 1所示预应力筋引起的预应力等效荷载[1-3]大小及分布见图 2.图 2所示的预应力等效荷载作用下,框架梁的综合弯矩见图 3.

|
图 2 线形1的等效荷载 Figure 2 Equivalent load of profile 1 |
|
图 3 线形1的综合弯矩 (kN·m) Figure 3 Combined bending moment of profile 1 (kN·m) |
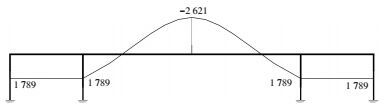
若忽略框架柱对图 1所示的框架梁的约束作用,即将图 1所示的各跨框架梁假想为简支梁,则在图 2所示的等效荷载作用下可确定主弯矩分布见图 4.
|
图 4 线形1的主弯矩 (kN·m) Figure 4 Main bending moment of profile 1 (kN·m) |
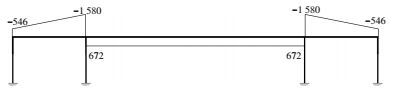
由于次弯矩等于综合弯矩与主弯矩之差,即可将图 4所示的主弯矩反号与图 3所示的综合弯矩叠加后可获得张拉引起的次弯矩分布,见图 5.
|
图 5 线形1次弯矩 (kN·m) Figure 5 Secondary moment of profile 1 (kN·m) |
将同一结构大中跨与两小边跨统一考虑,调整图 1所示的预应力筋线形为三段连续正反抛物线布置,见图 6.
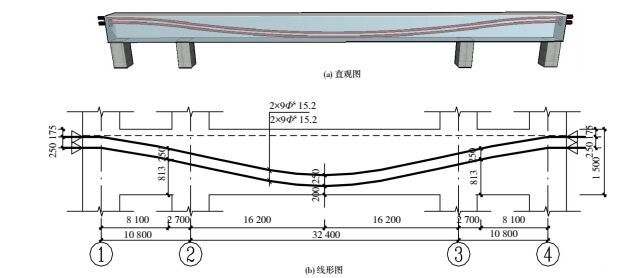
|
图 6 按线形2布置预应力筋 (mm) Figure 6 Prestressing tendons arranged as profile 2(mm) |
同样,考虑全部预应力损失后的有效预应力为1 000 N/mm2,可获得图 6所示线形对应的预应力等效荷载, 见图 7.

|
图 7 线形2的等效荷载 Figure 7 Equivalent load of profile 2 |
图 7所示的预应力等效荷载作用下,框架梁的综合弯矩见图 8.
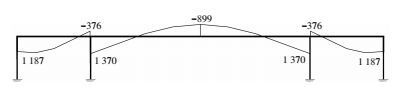
|
图 8 线形2的综合弯矩 (kN·m) Figure 8 Combined bending moment of profile 2 (kN·m) |
若忽略框架柱对图 6所示的框架梁的约束作用,即将图 6所示的框架梁认为是简支梁,则在图 7所示的等效荷载作用下可确定张拉引起的主弯矩分布, 见图 9.
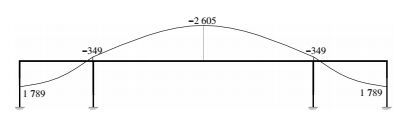
|
图 9 线形2的主弯矩 (kN·m) Figure 9 Main bending moment of profile 2 (kN·m) |
仍取次弯矩等于综合弯矩与主弯矩之差,即将图 9所示的主弯矩反号与图 8所示的综合弯矩叠加后可获得张拉引起的次弯矩分布[4],见图 10.

|
图 10 线形2的次弯矩 (kN·m) Figure 10 Secondary moment of profile 2 (kN·m) |
所涉及的典型工程为某商业综合体6层采光天井相关区域布置的3根有粘结预应力混凝土梁,混凝土设计强度等级为C40,普通受力纵筋采用HRB400级,箍筋采用HPB300级,预应力钢筋采用公称直径为15.2 mm、抗拉强度标准值1 860 N/mm2的低松弛钢绞线.
作用在框架上的恒荷载标准值[5-6]为49.73 kN/m,活荷载标准值为17.40 kN/m,外荷载组合作用下框架梁的弯矩见图 11.

|
(括号外为标准组合值,括号内为基本组合值) 图 11 外荷载组合作用下结构弯矩图 (kN·m) Figure 11 Moment under external load combination (kN·m) |
其中,截面及其配筋见图 12.按上述两种线形条件下,分别对小跨边支座截面、小跨跨中截面、小跨内支座截面、中跨支座截面和中跨跨中截面共5个控制截面拉区边缘和压区边缘的应力,按弹性进行计算[7-10],结果见表 1.
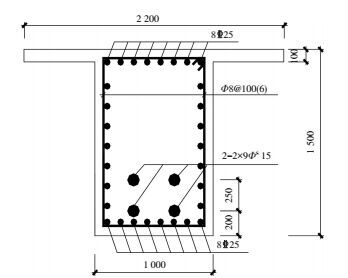
|
图 12 跨中截面配筋 Figure 12 Reinforcement of mid-span |
| 表 1 控制截面边缘应力 (取压应力为正) Table 1 Stress at control section edges (positive for compression stress) |
由表 1可知,在中跨支座截面、小跨内支座截面的顶部和中跨跨中截面的底部,均出现了不同量值的拉应力,对比可知,按照线形2布置预应力筋时,中跨支座截面顶部和中跨跨中截面底部的拉应力数值与按照线形1布置预应力筋时相比略大;而小跨边支座截面拉压区边缘最大拉压应力数值在按照不同线形布置预应力筋时相差不大,小跨跨中截面全截面处于受压状态,按照线形2布置预应力筋时更为有利.综上所述,按照线形2布置预应力筋会降低小跨跨中截面出现拉应力的可能,但同时会增大中跨跨中截面底部和中跨支座截面顶部的拉应力数值.
4 承载力分析在框架梁中非预应力筋布置相同的条件下 (As-=3 627 mm2, As+=3 627 mm2),采用上述两种预应力筋的线形布置,小跨内支座截面、小跨跨中截面、中支座截面和中跨跨中截面的承载力计算结果见表 2.
| 表 2 控制截面承载力 Table 2 Bearing capacity of critical sections |
由表 2可知,在所配非预应力钢筋相同的条件下,按照不同线形布置预应力钢筋,对小跨支座截面和中跨跨中截面的承载力没有影响,且均大于外荷载弯矩值;而对于中跨支座截面,按照线形2布置预应力钢筋时,由于减小了预应力钢筋的有效高度,降低了预应力筋的内力臂,其截面的承载力受到一定程度的削弱,而对于小跨跨中截面来说,由于增大了预应力钢筋的有效高度,增加了预应力筋的内力臂,其截面的承载力得到一定程度的提高.将控制截面承载力与外荷载弯矩值及次弯矩之和比较可知,按照线形1布置预应力筋,小跨支座、小跨跨中、中支座和中跨跨中的截面承载力均满足要求;按照线形2布置预应力筋,各控制截面承载力亦大于外荷载弯矩值与次弯矩之和,尤其是小跨跨中截面承载力具有较大富余,而中跨中支座截面的承载力富余量较小.以上分析说明将大跨及相邻的两小跨统一考虑将预应力筋按三段连续正反抛物线布置,不但可有效平衡大跨内的竖向荷载而且也平衡了小跨内的竖向荷载,但同时需要注意合理选择非预应力筋用量以保证中跨支座截面承载力的满足.
这里需要指出,若竖向外荷载作用下两小跨均表现为负弯矩,或因使用功能要求的小边跨梁截面高度小于大内跨梁高,也可采用如图 13所示的两种布置方式,一是将大跨所需的预应力筋按三段抛物线组成连续曲线,外伸至两小跨时分成两部分,一部分仍按直线延伸至边柱外边,另一部分则也按三段抛物线连续布置,见图 13(a);二是使线形1和线形2相结合,将大跨所需的预应力筋分为两部分,一部分按线形2将大内跨小边跨统一考虑取为三段抛物线连续曲线,另一部分则仅在大跨内按三段正反抛物线连续布置后按直线外伸至两小跨边柱外边,见图 13(b).相对而言,后者布置有利于减小预应力损失和保证有效预应力,在需满足包括内、边跨各控制截面的截面边缘拉压应力控制或裂缝控制要求,以及正截面承载力要求的前提下,也是预应力筋的一种优化布置.
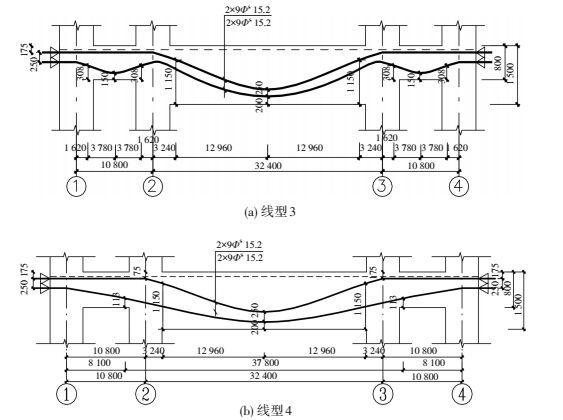
|
图 13 其他线形 (mm) Figure 13 Other profiles (mm) |
1) 大内跨小边跨混凝土框架结构中的预应力筋,若小跨跨度不大于大跨的1/3,可选择在大跨内连续布置 (线形1),也可选择将大小跨整体考虑为单跨,并按连续曲线布置 (线形2).
2) 按线形2布置预应力筋后,张拉产生的预应力等效荷载不但可较好平衡大跨承担的竖向外荷载,也可合理平衡小跨承担的竖向荷载.
3) 按线形2布置预应力筋后,大小跨相邻截面将产生一定量值的与外荷载弯矩效应相反的次弯矩,在非预应力筋布置合理的条件下,对保证正截面承载力有利.
| [1] |
周威, 郑文忠. 预应力等效荷载计算的通用方法及其简化[J].
哈尔滨工业大学学报, 2005, 37(1): 49-51.
ZHOU Wei, ZHENG Wenzhong. Unified method and simplification for calculating prestressing equivalent load[J]. Journal of Harbin Institute of Technology, 2005, 37(1): 49-51. |
| [2] |
孙宝俊. 预应力筋连续配筋的线形与等效荷载研究[J].
工业建筑, 1998, 28(11): 19-23.
SUN Baojun. Shape of continuous prestressing tendon and equivalent load research[J]. Industrial Architecture, 1998, 28(11): 19-23. DOI: 10.3321/j.issn:1000-8993.1998.11.005 |
| [3] |
陈永春, 陈国梅. 预应力超静定结构的等效荷载计算[J].
建筑结构学报, 1988, 9(2): 26-30.
CHEN Yongchun, CHEN Guomei. Calculation of equivalent load of prestressed statically indeterminate structure[J]. Journal of Building Structures, 1988, 9(2): 26-30. |
| [4] |
熊学玉, 孙宝俊. 有效预应力作用下预应力砼超静定结构的次弯矩计算[J].
建筑结构学报, 1994, 15(6): 55-63.
XIONG Xueyu, SUN Baojun. Calculation of second moment of prestressed statically structure under effective prestress[J]. Journal of Building Structures, 1994, 15(6): 55-63. |
| [5] |
建筑结构荷载规范: GB 50009—2012[S]. 北京: 中国建筑工业出版社, 2012.
Load code for the design of building structures: GB 50009—2012[S]. Beijing: China Architecture and Building Press, 2012. |
| [6] |
建筑结构可靠度设计统一标准: GB 50068—2001[S]. 北京: 中国建筑工业出版社, 2001.
Unified standard for reliability design of building structures: GB 50068—2001[S].Beijing: China Architecture and Building Press, 2001. |
| [7] |
混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2011.
Code for design of concrete structures: GB 50010—2010[S]. Beijing: China Architecture and Building Press, 2011. |
| [8] |
预应力混凝土结构设计规范: JGJ 369—2016[S]. 北京: 中国建筑工业出版社, 2016.
Code for design of prestressed concrete structures: JGJ 369—2016[S]. Beijing: China Architecture and Building Press, 2016. |
| [9] |
混凝土结构加固技术规范: GB 50367—2013[S]. 北京: 中国建筑工业出版社, 2013.
Design code for strengthening concrete structure: GB 50367—2013[S]. Beijing: China Architecture and Building Press, 2013. |
| [10] |
混凝土结构工程施工规范: GB 50666—2011[S]. 北京: 中国建筑工业出版社, 2012.
Code for construction of concrete structures: GB 50666—2011[S].Beijing: China Architecture and Building Press, 2012. |
 2017, Vol. 49
2017, Vol. 49


