2. 亚热带建筑科学国家重点实验室 (华南理工大学), 广州510640
2. State Key Laboratory of Subtropical Building Science (South China University of Technology), Guangzhou 510640, China
混凝土U型薄壁梁作为一种新型桥梁结构,具有建筑高度低、隔音效果好、施工周期短的优点,在城市轨道交通与道路桥梁工程中被广泛应用.实际工况下的混凝土U型薄壁桥梁会受到偏心荷载、列车摇摆、横向风荷载以及地震荷载的作用,桥梁常处于受扭状态.扭矩作用下,开口薄壁构件 (如U型薄壁梁) 的受力机理与传统的封闭截面构件 (如矩形梁、箱型梁) 完全不同[1].封闭截面构件受扭后主要发生自由扭转,仅产生环绕截面周边均匀分布的封闭剪力环流,而开口薄壁构件受扭后同时发生自由扭转和翘曲扭转,翘曲扭转作用下开口薄壁构件会产生翘曲弯矩和翘曲扭矩,以及明显的纵向翘曲变形与应力.翘曲弯矩产生翘曲正应变与翘曲正应力,翘曲扭矩则产生沿壁厚均匀分布且绕截面周边不闭合的剪力流.开口薄壁构件截面总扭矩等于自由扭矩与翘曲扭矩之和,两种扭矩产生截然不同的剪应力分布且其相对比例随扭转刚度而变化.因此,U型薄壁构件受扭分析实际上是自由扭转和翘曲扭转的耦合作用分析.
已有的研究成果主要针对混凝土封闭截面受扭构件的自由扭转,其理论基础为空间桁架模型理论.该理论最早由Rausch[2]于1929年提出,之后被多位学者发展完善,如Thurlimann等[3]提出变角空间桁架模型,Mitchell等[4]提出的斜压场理论,Hsu等[5]提出考虑混凝土软化的空间桁架模型等等.但是桁架模型仅适用于可以形成封闭剪力环流的自由扭转情况,对于开口薄壁构件的扭转问题,空间桁架理论无法单独解决.
开口薄壁受扭构件的研究成果较为匮乏,目前有参考价值的文献仅见Krpan等[6]于1981年完成的U型梁纯扭试验研究与抗扭承载力的理论分析,以及Luccioni等[7]运用转化矩阵方法建立的U型薄壁构件受扭分析模型.但是,上述分析模型仅考虑了翘曲弯矩效应,没有考虑翘曲扭转与自由扭转的耦合效应.
本文基于Vlasov开口薄壁梁弹性理论与受扭空间桁架模型,推导了钢筋混凝土U型薄壁截面受扭构件非线性分析模型,该模型既考虑了钢筋混凝土材料非线性本构关系,也兼顾了薄壁构件几何非线性变形特征以及开口构件翘曲扭转与自由扭转的耦合效应.利用所编制的分析程序,对5根钢筋混凝土U型薄壁受扭构件进行全过程分析,分析结果与试验数据吻合较好.
1 模型推导 1.1 总体思路与基本假定根据Vlasov弹性开口薄壁梁理论,截面自由扭矩和翘曲扭矩可分别按下列公式计算:
| $ {T_{\rm{s}}} = GK\varphi '\left( z \right), $ | (1) |
| $ {T_{\rm{\omega }}} = - E{I_{{\rm{\omega \omega }}}}\varphi '''\left( z \right). $ | (2) |
式中:Ts为自由扭矩,Tω为翘曲扭矩,E与G分别为材料的弹性模量与剪切模量,K与Iωω分别表示截面的极惯性矩与主扇性惯性矩,φ表示截面的扭转角.乘积GK称为截面的自由扭转刚度,乘积EIωω称为截面的翘曲扭转刚度.受扭构件任意截面的总扭矩等于该截面的自由扭矩与翘曲扭矩之和,由此得到截面平衡微分方程:
| $ GK\varphi '\left( z \right) - E{I_{{\rm{\omega \omega }}}}\varphi '''\left( z \right) = T\left( z \right). $ | (3) |
上式描述了U型薄壁纯扭构件任意截面的平衡关系,其中GK与EIωω的计算包含了截面的几何关系与材料的本构关系,微分方程 (3) 描述了一个受扭变形场,当边界条件确定后,微分方程的解会给出构件整体扭转变形与内力的分布情况.
对于弹性匀质构件,各截面的刚度GK与EIωω保持恒定,所以上述微分方程是线性微分方程,可以得到解析解.对于钢筋混凝土构件,由于混凝土裂缝发展造成截面刚度损失,各截面的刚度GK与EIωω会随着截面内力与变形的增大而不断衰减,换言之,GK与EIωω是截面扭转变形量 (扭转角φ及其各阶导数) 的函数.所以对于钢筋混凝土构件,微分方程 (3) 会表现为复杂的非线性微分方程形式,且很难得到解析解,如式 (4) 所示.
| $ \begin{array}{l} GK\left( {\varphi ,\varphi ',\varphi '',\varphi '''} \right)\varphi '\left( z \right) - \\ \;\;\;\;E{I_{{\rm{\omega \omega }}}}\left( {\varphi ,\varphi ',\varphi '',\varphi '''} \right)\varphi '''\left( z \right) = T\left( z \right). \end{array} $ | (4) |
综上可见,如果通过截面分析分别建立截面翘曲扭转刚度EIωω与自由扭转刚度GK随截面扭转变形的变化规律,那么结合式 (4) 可以得到受扭构件截面平衡微分方程的显式形式,然后通过微分方程的数值解法可以得到方程 (4) 得到数值解进而得到构件受力和变形的详细情况.以上便是本文模型推导的总体思路,它包含了3个层次:截面翘曲扭转刚度分析,截面自由扭转刚度分析,截面平衡微分方程的建立与求解.具体推导过程详见1.2~1.4,另外,本文推导过程基于以下假定:
1) 刚周边假定.截面外形轮廓线在自身平面内保持刚性,但可以产生出平面翘曲;
2) 钢筋与混凝土之间充分粘结,无相对滑移;
3) 认为翘曲扭转刚度主要受翘曲正应力影响,而自由扭转刚度主要受自由扭矩和翘曲扭矩引起的剪应力的影响.
1.2 截面的翘曲扭转刚度由前面的总体思路可知,本小节的中心任务是推导求解U型薄壁构件任意截面翘曲扭转刚度随扭转角的变化规律.
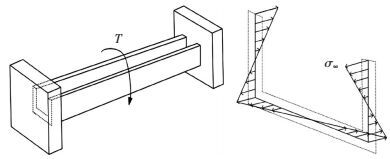
1.2.1 截面几何协调方程与翘曲平衡方程根据Vlasov理论,U型薄壁构件受扭时,截面会产生线性分布的纵向翘曲正应变,当构件纵向变形被约束时,就会产生翘曲正应力,见图 1.截面上任意一点处的翘曲正应变按式 (5) 求解.
|
图 1 U型薄壁受扭构件翘曲正应力分布 Figure 1 Distribution of warping normal stress in U-shaped thin-walled member under pure torsion |
| $ {\varepsilon _{\rm{\omega }}} = \varphi ''\left( z \right)\omega \left( s \right). $ | (5) |
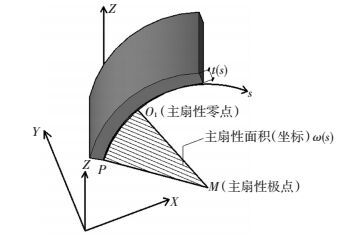
式中:εω表示任意点的翘曲正应变,φ表示该截面扭转角,ω表示该点的主扇性坐标.主扇性坐标是一类面积坐标,见图 2.任意点P的主扇性坐标的几何含义为:由极点M向弧长坐标s处的主扇性零点O1引连线并沿逆时针方向旋转到P所扫过面积的两倍.图 2给出了3类坐标系的示意图:直角坐标系 (x,y,z)、弧长坐标系 (s,z)、扇性坐标系 (ω,s).每种坐标系均可以定位构件任意截面上的任意点.由式 (5) 可知,任意截面翘曲正应变的分布规律与主扇性坐标ω相同.
|
图 2 主扇性坐标示意 Figure 2 Principal sectorial coordinate |
对于弹性匀质截面,翘曲正应力σω可按式 (6) 计算,式中E为材料弹性模量.σω乘以相应主扇性坐标ω后对整个截面进行面积积分可以得到翘曲弯矩Mω,见式 (7).
| $ {\sigma _{\rm{\omega }}} = E\varphi ''\left( z \right)\omega \left( s \right), $ | (6) |
| $ {M_{\rm{\omega }}} = - E{I_{{\rm{\omega \omega }}}}\varphi ''\left( z \right), $ | (7a) |
| $ {I_{{\rm{\omega \omega }}}} = \int_A {{\omega ^2}{\rm{d}}A} . $ | (7b) |
翘曲弯矩Mω可类比初等弯曲理论中的弯矩,这里主扇性坐标ω起到了力臂的作用.面积积分Iωω称为主扇性惯性矩,是一类截面几何参数.通过式 (2) 与 (7a) 可以发现,翘曲弯矩Mω与翘曲扭矩Tω之间存在导数关系.
1.2.2 混凝土和钢筋的材料本构关系混凝土受压采用Vecchio与Collins于1982年提出的软化本构关系:
| $ {\sigma _{\rm{d}}} = {f_{\rm{c}}}\left[ {2\left( {\frac{{{\varepsilon _{\rm{d}}}}}{{{\varepsilon _0}}}} \right) - \lambda {{\left( {\frac{{{\varepsilon _{\rm{d}}}}}{{{\varepsilon _0}}}} \right)}^2}} \right],{\varepsilon _{\rm{d}}} \le {\varepsilon _0}/\lambda ; $ | (8a) |
| $ {\sigma _{\rm{d}}} = \frac{{{f_{\rm{c}}}}}{\lambda }\left[ {1 - 0.15{{\left( {\frac{{{\varepsilon _{\rm{d}}} - {\varepsilon _0}/\lambda }}{{2{\varepsilon _{\rm{0}}} - {\varepsilon _0}/\lambda }}} \right)}^2}} \right],{\varepsilon _0}/\lambda \le {\varepsilon _{\rm{d}}} \le {\varepsilon _{\rm{u}}}. $ | (8b) |
式中:fc为混凝土轴心抗压强度; 对于一般混凝土,ε0=0.002, εu=0.003 3;λ为混凝土受压软化系数, 对于单轴受压状态,λ=1.在处理翘曲问题时,可按照λ=1对应的单轴受压本构关系进行计算.
采用式 (9) 所示的江见鲸等[8]受拉混凝土本构关系,即受拉开裂前应力应变呈线性关系,开裂后应力呈指数衰减.
| $ {\sigma _{\rm{r}}} = \frac{{{f_{\rm{c}}}}}{{{\varepsilon _{{\rm{cr}}}}}}{\varepsilon _{\rm{r}}},{\varepsilon _{\rm{r}}} \le {\varepsilon _{{\rm{cr}}}}; $ | (9a) |
| $ {\sigma _{\rm{r}}} = {f_{\rm{t}}}{{\rm{e}}^{ - {\rm{\alpha }}\left( {{\varepsilon _{\rm{r}}} - {\varepsilon _{{\rm{cr}}}}} \right)}},{\varepsilon _{\rm{r}}} > {\varepsilon _{{\rm{cr}}}}. $ | (9b) |
式中:ft为混凝土轴心抗拉强度,εcr为混凝土开裂应变,α为与混凝土断裂能相关的参数,对普通混凝土α=10 000.
钢筋采用式 (10) 所示的本构关系:
| $ {\sigma _{\rm{s}}} = {E_{\rm{s}}}{\varepsilon _{\rm{s}}},{\varepsilon _{\rm{s}}} \le {\varepsilon _{\rm{y}}}; $ | (10a) |
| $ \sigma = \frac{{{f_{\rm{u}}} - {f_{\rm{y}}}}}{{{\varepsilon _{\rm{u}}} - {\varepsilon _{\rm{y}}}}}\left( {\varepsilon - {\varepsilon _{\rm{y}}}} \right) + {f_{\rm{y}}},{\varepsilon _{\rm{y}}} \le \varepsilon \le {\varepsilon _{\rm{u}}}. $ | (10b) |
式中:fy和fu分别为钢筋的屈服强度和极限强度,εy和εu分别为相应的屈服应变和极限应变.
1.2.3 截面翘曲刚度的非线性描述1.2.1节中的公式是基于弹性匀质构件推导出的.对于非线性特征较强的钢筋混凝土构件,还需考虑以下两方面问题:1) 将钢筋与混凝土两种刚度相差很大的材料等效为均质材料;2) 随着荷载增大,截面混凝土开裂造成材料参数与几何参数持续弱化,截面形心C与主扇性极点M的位置,主扇性坐标ω的分布会相应地变化,截面刚度不断衰减,这同时包含了材料非线性问题与薄壁构件几何非线性问题.
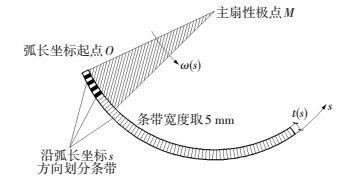
针对上述问题,本小节引入截面条带积分算法和条带面积的等刚度变换方法来解决钢筋与混凝土的材料等效问题.在等效均质材料的基础上, 通过材料非线性本构关系式 (8)~(10) 并结合均质截面形心与主扇性极点位置的计算方法来考虑材料非线性与几何非线性问题,建立了描述截面翘曲变形与内力的非线性方程组.最后通过割线刚度法求解所建立的非线性方程组,得出截面翘曲扭转刚度随截面扭转变形的衰减规律曲线.截面条带划分按照图 3所示方法进行,条带宽度取5 mm,然后按照式 (11) 对条带面积进行等刚度变换.
|
图 3 条带划分 Figure 3 Strip partition |
| $ {A_{{\rm{e}}i}} = {A_{{\rm{c}}i}}\frac{{{E_{\sec \_{\rm{c}}}}\left( \varepsilon \right)}}{{{E_0}}} + {A_{{\rm{s}}i}}\frac{{{E_{\sec \_{\rm{s}}}}\left( \varepsilon \right)}}{{{E_0}}}. $ | (11) |
式中:Aei为第i条条带变换后的折算面积,Asi为第i条条带中钢筋的截面积,Aci为第i条条带中混凝土的面积,Esec_c(ε) 与Esec_s(ε) 分别为根据本构关系 (8)~(10) 计算出的当前应变下混凝土与钢筋的割线模量,E0为混凝土初始弹性模量.
完成截面条带划分与等效刚度变换后,截面积分可以离散成求和形式,如截面扇性惯性矩Iωω可按式 (12) 计算,式中Aei指第i条条带的折算面积.式 (12) 乘以混凝土初始弹性模量E0即为截面当前受力状态下的翘曲扭转刚度EIωω.
| $ {I_{{\rm{\omega \omega }}}} = \int_A {{\omega ^2}{\rm{d}}A} = \sum\limits_{i = 1}^n {{A_{{\rm{e}}i}}\omega _i^2} . $ | (12) |
随着荷载增加,截面形心C与主扇性极点M不断移动,主扇性坐标ω的分布随之变化,截面翘曲扭转刚度EIωω不断衰减,因此每一级荷载下形心C的位置可以由式 (13a) 与 (13b) 确定:
| $ {x_{\rm{c}}} = \sum\limits_{i = 1}^n {{A_{{\rm{e}}i}}{x_i}} /\sum\limits_{i = 1}^n {{A_{{\rm{e}}i}}} , $ | (13a) |
| $ {y_{\rm{c}}} = \sum\limits_{i = 1}^n {{A_{{\rm{e}}i}}{y_i}} /\sum\limits_{i = 1}^n {{A_{{\rm{e}}i}}} . $ | (13b) |
式中:xc与yc为形心C的直角坐标,xi与yi为第i条条带形心处的直角坐标.以当前截面形心C为极点,截面上任意一点为零点,建立辅助扇性坐标系ωA.根据Vlasov理论,当前主扇性极点M的位置可以由辅助扇性坐标系ωA和全局直角坐标系Oxy来确定,参见式 (13c)~(13e):
| $ {a_x} = \frac{{{I_y}{I_{{\omega _A}x}} - {I_{xy}}{I_{{\omega _A}y}}}}{{{I_x}{I_y} - I_{xy}^2}}, $ | (13c) |
| $ {a_y} = \frac{{{I_x}{I_{{\omega _A}y}} - {I_{xy}}{I_{{\omega _A}x}}}}{{{I_x}{I_y} - I_{xy}^2}}, $ | (13d) |
| $ \beta = - \frac{{{S_{{\omega _A}}}}}{A}. $ | (13e) |
式中:ax与ay为主扇性极点M与辅助扇形极点C之间的直角坐标差值; ax、ay、xc、yc四个参数即可确定当前受力状态下主扇性极点M的位置; β为主扇性零点在辅助扇性坐标系ωA中的扇性坐标,用来确定主扇性零点的位置.公式 (13c)~(13e) 等号右侧是全局直角坐标系Oxy中各类截面面积积分,以及辅助扇性坐标系ωA中各类扇性面积积分,这些几何参数均可由离散条带求和的方法计算:
| $ {I_x} = \sum\limits_{i = 1}^n {{A_{{\rm{e}}i}}y_i^2} ,{I_x} = \sum\limits_{i = 1}^n {{A_{{\rm{e}}i}}x_i^2} ,{I_{xy}} = \sum\limits_{i = 1}^n {{A_{{\rm{e}}i}}{x_i}{y_i}} , $ | (13f) |
| $ {I_{{\omega _A}x}} = \sum\limits_{i = 1}^n {{A_{{\rm{e}}i}}{\omega _{Ai}}{y_i}} ,{I_{{\omega _A}y}} = \sum\limits_{i = 1}^n {{A_{{\rm{e}}i}}{\omega _{Ai}}{x_i}} , $ | (13g) |
| $ {S_{{\omega _A}}} = \sum\limits_{i = 1}^n {{A_{{\rm{e}}i}}{\omega _{Ai}}} ,A = \sum\limits_{i = 1}^n {{A_{{\rm{e}}i}}} . $ | (13h) |
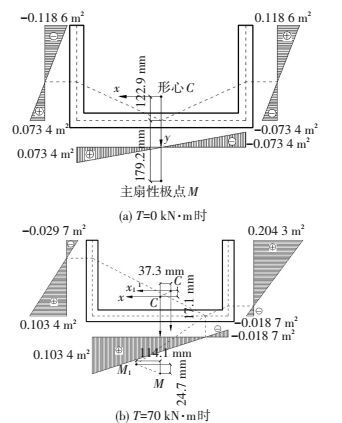
以后文所述TWB-A试验梁为例 (尺寸见表 1与图 15),图 4(a)为截面不受力时主扇性坐标ω分布图,图 4(b)为扭矩70 kN·m时计算的ω分布图.可见,扭矩70 kN·m时相对于初始位置, 形心C向右和向上分别移动了37.3 mm和17.1 mm,主扇性极点M向左和向上分别移动了114.1 mm和24.7 mm,说明截面几何参数发生了显著变化.
| 表 1 试件材料参数 Table 1 Material parameters of test specimens |
|
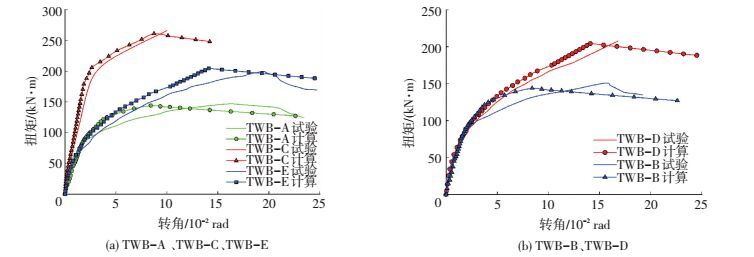
图 15 扭矩-转角试验曲线与分析曲线 Figure 15 Testing and analysis curves of torque-rotation |
|
图 4 截面主扇性坐标的分布 Figure 4 Distribution of principal sectorial coordinate |
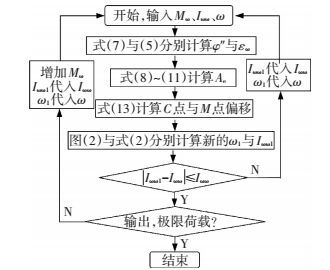
式 (5)~(13) 构成了描述截面翘曲内力与变形关系的非线性方程组,本文采用割线刚度迭代法求解该方程组,并设计了相应的计算程序,程序流程参见图 5.
|
图 5 翘曲扭转刚度计算程序流程图 Figure 5 Flowchart of calculation program for warping torsional stiffness |
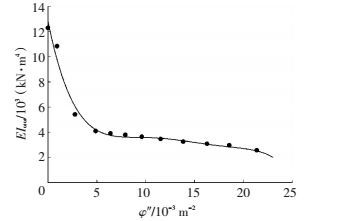
同样以TWB-A试验梁截面为例,按照上述算法可计算出U型构件任意截面翘曲扭转刚度EIωω随φ″的衰减曲线,见图 6.为了方便后文建立和求解构件平衡微分方程,可以运用最小二乘法将计算出的散点拟合成EIωω关于φ″的显式函数,具体过程不再赘述.
|
图 6 翘曲扭转刚度EIωω衰减规律 (TWB-A) Figure 6 Attenuation law of warping torsional stiffness EIωω(TWB-A) |
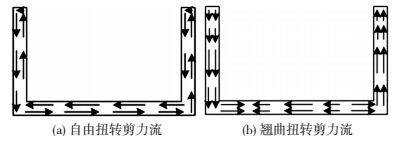
同样由总体思路可知,本小节的中心任务是推导求解U型薄壁构件任意截面自由扭转刚度随扭转角的变化规律.由假定 (3) 可知,截面的自由扭转刚度GK主要受截面剪应力的影响.而自由扭矩Ts与翘曲扭矩Tω的联合作用使截面剪力流的分布比较复杂:自由扭矩Ts引起沿截面均匀分布,内外壁方向相反的闭合剪应力环流qs,见图 7(a);翘曲扭矩Tω引起的剪力流qω沿壁厚方向均匀分布,沿弧长坐标s方向变化且不闭合,见图 7(b).为了简化分析,这里计算qω的平均值.
|
图 7 截面剪力流分布 Figure 7 Distribution of shear flow at cross section |
根据空间桁架理论,将U型薄壁截面等效成图 8所示的3块空心平板[9-10],截面在Ts与Tω的联合作用下会形成图 8所示的剪力流,qω与qs可出现三类不同的叠加情况.根据剪力流的大小,可把空心平板的侧壁分为三类薄片,编号为①、②、③,相应剪力流的大小分别为q1、q2、q3,记为qi(i=1, 2, 3);相应薄片的有效厚度为t1、t2、t3,记为ti(i=1, 2, 3).剪力流的计算公式为:

|
图 8 截面简化 Figure 8 Simplified section |
| $ {q_{\rm{s}}} = \frac{{{T_{\rm{s}}}}}{{2{A_0}}}, $ | (14) |
| $ {q_{\rm{\omega }}} = - \frac{{{T_{\rm{\omega }}}\int_l {{S_{\rm{\omega }}}{\rm{d}}\omega } }}{{{I_{{\rm{\omega \omega }}}}\int_l {{\rm{d}}\omega } }} = \frac{{{T_{\rm{s}}}}}{{k\sum\limits_{i = 1}^6 {\left| {{\omega _i}} \right|} }}, $ | (15) |
| $ {q_1} = {q_{\rm{s}}}, $ | (16a) |
| $ {q_2} = {q_{\rm{s}}} - {q_{\rm{\omega }}}, $ | (16b) |
| $ {q_3} = {q_{\rm{s}}} + {q_{\rm{\omega }}}, $ | (16c) |
| $ {A_0} = \left( {{b_0} + 2{h_0} - 2t - 3{t_1}} \right)\left( {t - \frac{{{t_2} + {t_3}}}{2}} \right). $ | (16d) |
式中:b0和h0分别为截面的宽度和高度,t为薄壁的厚度,k为自由扭矩与翘曲扭矩的比,即k=Ts/Tω,ωi(i=1~6) 为构件底板和腹板两端的扇性坐标值 (即图 8中P1~P6六点),A0为剪力流包围的面积.根据剪力流的定义,有如下关系成立:
| $ {q_i} = {\tau _i}{t_i}. $ | (17) |
截面简化后,首先分析薄片的内力和变形,再将薄片组合即可得到U型截面的内力与变形.薄片的组合必须满足两个条件:其一是平衡条件,也即满足式 (17);其二是协调条件,也即各薄片的扭转角必须相同,截面整体的扭转角必须唯一.本节会详细讨论上述计算过程,着重求解自由扭转刚度GK随φ′衰减规律.
1.3.1 自由扭转时截面变形协调条件薄片的应变分量必须满足变形协调条件,首先根据假定 (2),混凝土与钢筋具有相同的纵向应变和横向应变,如式 (18) 所示.
| $ {\varepsilon _{l{\rm{c}}}} = {\varepsilon _{l{\rm{s}}}},{\varepsilon _{{\rm{tc}}}} = {\varepsilon _{{\rm{ts}}}}. $ | (18) |
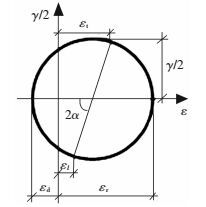
式中:εlc与εls分别为混凝土与钢筋的纵向应变,统一记为εl;εtc与εts分别为混凝土与钢筋的横向应变,统一记为εt.此外,每块薄片单元中的纵向应变εl、横向应变εt、剪应变γ还需满足应变莫尔圆关系,见图 9.
|
图 9 莫尔应变圆 Figure 9 Mohr strain circle |
图 9中,εd为混凝土的主压应变,εr为混凝土的主拉应变,α为主压应变方向与构件纵向的夹角,εr以受拉为正,εd受压为正.这里增加下标i区分不同薄片,比如薄片1、2、3中相应的混凝土主压应变统一记为εdi(i=1, 2, 3).
1.3.2 自由扭转时截面平衡条件忽略钢筋的栓销作用,则剪应力均由混凝土承受,由薄片单元纵向与横向受力平衡可得:
| $ {\sigma _l} = {\rho _l}{\sigma _{l{\rm{s}}}}, $ | (19) |
| $ {\sigma _{\rm{t}}} = {\rho _{\rm{t}}}{\sigma _{{\rm{ts}}}}. $ | (20) |
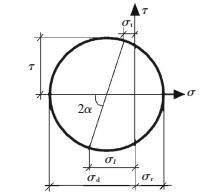
式中:σl与σt为混凝土的纵向应力与横向应力,σls与σts分别为纵向钢筋与横向箍筋中的应力,ρl与ρt分别为纵向钢筋与横向箍筋的配筋率.根据空间桁架理论,混凝土受剪会产生斜裂缝,斜裂缝将混凝土分成多个斜压杆,其方向与主压应力方向一致,见图 10,图中各应力分量还须满足莫尔应力圆条件,见图 11,图 11中应力分量的命名规则与莫尔应变圆相同.

|
图 10 混凝土受力单元 Figure 10 Concrete mechanical unit |
|
图 11 莫尔应力圆 Figure 11 Mohr stress circle |
材料本构关系的选用与1.2.2中式 (8)~(10) 相同,不过这里混凝土处于二向应力状态,由于主拉应变的存在,混凝土在主压应力方向上会发生软化现象,所以这里软化系数λ>1,并且与主拉应变的大小相关,需要按照式 (21) 进行计算[11].
| $ \frac{1}{\lambda } = \frac{{0.9}}{{\sqrt {1 + 400{\varepsilon _{\rm{r}}}} }}. $ | (21) |
将钢筋本构关系 (10) 分别代入式 (19)、(20) 消去σls与σts,并结合图 9、11所示的莫尔应力应变关系可得:
| $ {\tan ^2}\alpha = \frac{{{\sigma _{\rm{d}}} + {\rho _l}{E_{\rm{s}}}{\varepsilon _{\rm{d}}}}}{{{\sigma _{\rm{r}}} + {\rho _l}{E_{\rm{s}}}{\varepsilon _{\rm{r}}}}}, $ | (22) |
| $ {\varepsilon _{\rm{r}}} = {\varepsilon _{\rm{d}}}{\tan ^2}\alpha + \frac{{{\sigma _{\rm{d}}}{{\tan }^2}\alpha }}{{{\rho _{\rm{t}}}{E_{\rm{s}}}}} - \frac{{{\sigma _{\rm{r}}}}}{{{\rho _{\rm{t}}}{E_{\rm{s}}}}}. $ | (23) |
上式中Es为钢筋的弹性模量.经上述代换,可以形成5个独立方程式,包括材料本构关系式 (8)、(9)、(21) 以及内力变形关系式 (22)、(23),其中包含6个独立变量:εd、εr、σd、σr、λ、α,给定任意一个变量就可以求出其余5个变量.本文给定εd,通过解上述方程组求得其余5个变量,进而根据莫尔圆求得剪应力τ与剪应变γ,这在后文的计算程序会有体现.
根据空间桁架理论,单块薄板的扭转角可按照式 (24) 计算;截面整体的扭转角可按照Bredt薄管理论由剪应变的曲线积分得到,参见式 (25).
| $ \varphi ' = \frac{{2{\varepsilon _{\rm{d}}}}}{{{t_i}\sin 2\alpha }}, $ | (24) |
| $ \oint_l {\gamma {\rm{d}}s} = 2{A_0}\varphi '. $ | (25) |
结合图 9,式 (25) 可化简为:
| $ \varphi ' = \frac{{{\gamma _1}\left( {6t - 3{t_2} - 2{t_3}} \right) + \left( {{\gamma _2} + {\gamma _3}} \right)\left( {{b_0} + 4{h_0} - 2t - 5{t_1}} \right)}}{{2{A_0}}}. $ | (26) |
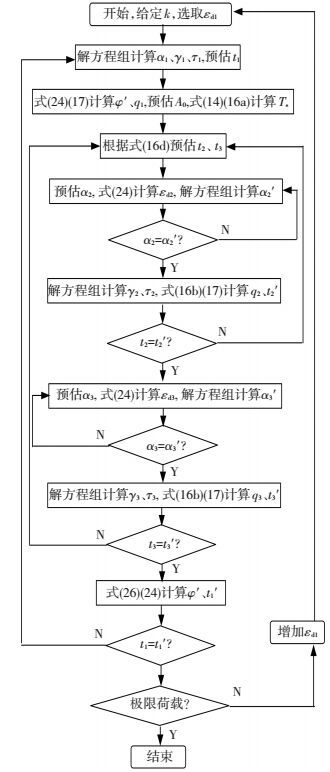
式 (26) 中γ1、γ2、γ3分别为薄片①、②、③ 中混凝土的剪应变.如果截面满足协调条件,则分别按照式 (24) 与 (26) 计算出的φ′相等.至此,可以总结得到求解U型薄壁构件任意截面GK-φ′曲线的算法,算法流程见图 12.
|
图 12 自由扭转计算程序总流程图 Figure 12 Flowchart of calculation program for Saint Venant torsion |
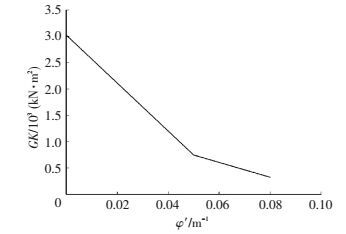
以TWB-A试验梁为例,图 13是该梁任意截面按上述算法及割线迭代方法[12-13]得到的GK随φ′的衰减曲线.计算结果十分接近双折线,同样可以用最小二乘法拟合成GK关于φ′的显式函数.
|
图 13 自由扭转刚度GK衰减规律 (TWB-A) Figure 13 Attenuation law of Saint Venant torsional stiffness GK (TWB-A) |
1.2与1.3小节分别得到了EIωω-φ″与GK-φ′全过程曲线,将所得的刚度函数代入式 (3) 可以建立描述构件整体变形场的微分方程:
| $ {F_{\rm{s}}}\left( {\varphi '} \right)\varphi '\left( z \right) - {F_{\rm{\omega }}}\left( {\varphi ''} \right)\varphi '''\left( z \right) = T\left( z \right). $ | (27) |
上式中Fs代表按照1.3小节中算法求得的自由扭转刚度函数,Fω代表按照1.2小节中方法求得的翘曲扭转刚度函数.
一般来说,按照式 (27) 所建立的微分方程是高阶非线性微分方程,很难得到解析解,但是可以利用数值方法求解.本节采用经典四阶龙格—库塔 (Runge-Kutta) 方法求解微分方程在结点处的数值解,并编制了相应的计算程序,求解步长取0.1 m.至此全部计算模型与求解算法已构建完毕,整个计算过程需要按顺序执行本文提出的翘曲扭转计算程序、自由扭转计算程序、非线性微分方程求解程序3个程序模块,程序总运算时间需要15 min.
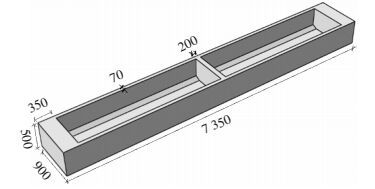
2 非线性分析结果与试验结果对比为验证所提出计算模型的准确性,运用上述算法对5根U型薄壁试验梁进行了全过程模拟分析.5根试验梁的编号为TWB-A~TWB-E,其中TWB-C由Collins于1981年设计完成,其余4根由本项目组设计并完成试验[14].试验梁的示意图与材料参数见图 14与表 1.表 1中fc为混凝土轴心抗压强度,fy为钢筋屈服强度,单位均为MPa,d代表钢筋直径,单位为mm.
|
图 14 试验梁示意 Figure 14 Beam specimen |
5根试验梁均采取两端固结、跨中施加集中扭矩的边界条件.图 15给出了5根试验梁的扭矩-转角曲线的试验结果和模拟分析结果.总体上计算曲线与试验曲线吻合良好,但在接近峰值荷载处,扭转角的计算值小于试验值.造成这种现象的主要原因是试验梁同批次的混凝土仅测定了弹性模量和棱柱体抗压强度,而屈服应变和极限压应变均按照规范取值,可能使所选用的混凝土本构关系刚度偏大,从而导致扭转角的计算值偏小.
表 2对比了出现弯曲裂缝荷载、斜裂缝荷载、屈服荷载以及极限荷载的计算值与试验值,表中Texp为试验值,Tcalc为计算值,单位kN·m.除TWB-A的斜裂缝荷载计算值与试验值差距较大外,U型薄壁构件的弯曲裂缝荷载、纵筋屈服荷载和极限荷载的试验结果与计算结果均吻合较好.表 2中4项 (共20个数据) 试验值与计算值比值的平均值为1.014,标准差为0.127,变异系数为0.126.
| 表 2 特征荷载点对比 Table 2 Comparison of feature loads |
1) 基于Vlasov开口薄壁梁理论和空间桁架模型, 本文推导建立了U型薄壁钢筋混凝土受扭构件非线性分析模型, 该模型考虑了材料非线性和薄壁几何非线性问题,同时兼顾了自由扭转与翘曲扭转的耦合作用效应.
2) 编制了与分析模型相应的分析程序,并对5根U型薄壁钢筋混凝土受扭试验梁进行了非线性全过程分析.分析结果与试验数据均吻合较好,从而验证了所提非线性分析模型的正确性.
| [1] | VLASOV V Z. Thin-walled elastic beams[M]. New York: National Technical Information Service, 1984: 111-167. |
| [2] | RAUSCH E. Design of reinforced concrete in torsion (Berechnung des eisenbetons gegen verdrehung)[D]. Berlin: Technische Hochschule, 1929. |
| [3] | THURLIMANN B. Torsional strength of reinforced and prestressed concrete beams-CEB approach[J]. ACI Special Publication, 1979, 59(5): 101-116. |
| [4] | MITCHELL D, COLLINS M P. Diagonal compression field theory-a rational model for structural concrete in pure torsion[J]. ACI Journal Proceedings, 1974, 71(8): 396-408. |
| [5] | HSU T T C, MO Y L. Softening of concrete in torsional members-theroy and tests[J]. ACI Journal Proceedings, 1985, 82(3): 290-303. |
| [6] | KRPAN P, COLLINS M P. Predicting torsional response of thin-walled open RC members[J]. Journal of the Structural Division, 1981, 107(6): 1107-1127. |
| [7] | LUCCIONI B M, REIMUNDíN J C, DANESI R. Thin-walled prestressed concrete members under combined loading[J]. Journal of Structural Engineering, 1996, 122(3): 291-297. DOI: 10.1061/(ASCE)0733-9445(1996)122:3(291) |
| [8] |
江见鲸, 陆新征, 叶列平.
混凝土结构有限元分析[M]. 北京: 清华大学出版社, 2005: 45-53.
JIANG Jianjing, LU Xinzheng, YE Lieping. Finite element analysis of concrete structures[M]. Beijing: Tsinghua University Publishing House, 2005: 45-53. |
| [9] |
顾平. 薄片模型在计算钢筋混凝土剪扭构件中的应用[J].
建筑结构学报, 1995(1): 41-49.
GU Ping. Panelmodel in analyzing RC members subjected to torsion and shear[J]. Journal of Building Structures, 1995(1): 41-49. DOI: 10.14006/j.jzjgxb.1995.01.005 |
| [10] |
余报楚, 张哲, 高潮, 等. 混凝土桥面板的非线性有限元分析[J].
哈尔滨工业大学学报, 2007, 39(2): 318-321.
YU Baochu, ZHANG Zhe, GAO Chao, et al. Nonlinear FEM analysis for the concrete bridge deck slab[J]. Journal of Harbbin Institute of Technology, 2007, 39(2): 318-321. |
| [11] | BELARBI A, HSU T T C. Constitutive laws of softened concrete in biaxial tension compression[J]. ACI Structural Journal, 1995, 92(5): 191-203. |
| [12] |
焦俊婷, 叶英华, 刁波. 不规则截面钢筋混凝土梁柱单元模型及应用[J].
哈尔滨工业大学学报, 2008, 40(4): 636-639.
JIAO Junting, YE Yinghua, DIAO Bo. Element model of reinforced concrete members with irregularly shaped section and its application[J]. Journal of Harbin Institute of Technology, 2008, 40(4): 636-639. |
| [13] |
叶英华, 刘文鹏, 刁波. 基于BIM技术的混凝土截面时效非线性分析[J].
哈尔滨工业大学学报, 2012, 44(8): 106-112.
YE Yinghua, LIU Wenpeng, DIAO Bo. BIM-based time-dependent non-linear analysis of concrete section[J]. Journal of Harbbin Institute of Technology, 2012, 44(8): 106-112. DOI: 10.11918/j.issn.0367-6234.2012.08.021 |
| [14] | CHEN Shenggang, DIAO Bo, GUO Quanquan, et al. Experiments and calculation of U-shaped thin-walled members under pure torsion[J]. Engineering Structures, 2016, 106: 1-14. DOI: 10.1016/j.engstruct.2015.10.019 |
 2017, Vol. 49
2017, Vol. 49


