2. 广西华景城建筑设计有限公司,南宁530023
2. Guangxi Huajingcheng Architectural Design Co., Ltd., Nanning 530023, China
结构的连续倒塌是指由于结构某一构件的初始损伤造成的损伤在不同构件间发生传递,进而引起结构整体发生的不成比例破坏.自1968年英国Ronan Point公寓发生连续倒塌并造成严重后果之后,关于结构连续倒塌方面的研究得到广泛关注.但由于造成重大社会影响的连续倒塌事件一直再未发生,因此自1978年后的20年间,关于结构连续倒塌方面的研究逐渐趋于沉寂.随着2001年911事件的发生,关于结构连续倒塌的研究又重新得到重视.美国总务管理局 (GSA) 于2003年推出了连续倒塌分析与设计规程[1],美国国防部 (DoD) 于2005年推出了结构抗连续倒塌的设计规程[2],中国在2015年推出了建筑结构抗倒塌设计规范[3].
结构抗连续倒塌设计方法分两类:间接方法和直接方法.其中,间接方法主要是拉结强度法 (tie force method),直接方法包括:拆除构件法 (又称“替代荷载路径法”)(alternate path method) 和局部加强方法 (enhanced local strength method).近年来,拆除构件法不仅作为一种结构抗连续倒塌设计方法,更是作为一种结构抗连续倒塌能力评估方法,得到了工程人员的广泛应用.拆除构件法是评估结构在关键构件退出工作情况下,是否依然具有足够的维持整体稳定的能力,它包括:线性静力分析方法、线性动力分析方法、非线性静力分析方法和非线性动力分析方法.综合考虑计算精度和计算效率的平衡,非线性静力分析方法,又称为Pushdown方法[4],得到了更为广泛的应用[5].
Pushdown分析虽然可以确定结构的竖向极限承载能力,但无法模拟结构在关键构件失效后引发的动力效应.因此,为准确模拟结构连续倒塌这一强非线性动力反应过程,非线性动力分析方法的精度无疑要高于非线性静力分析方法的精度.随着非线性有限元分析方法的不断成熟和计算机性能的不断提升,采用非线性动力分析方法开展钢筋混凝土结构的抗连续倒塌能力评估已经得到广泛应用.例如:马高等[6]、吕大刚等[7]均对钢筋混凝土框架结构在瞬间失柱后的动力反应特性以及抗连续倒塌性能进行了研究.
在RC框架结构连续倒塌的非线性动力分析中,有几个问题尚需深入讨论:1) 失效时长.在非线性动力分析中,框架柱通常假设为瞬间失效.然而,在实际问题研究中,柱失效需要经过一定的时间长度,那么柱失效时长对结构的动力反应结果影响有多大?2) 重力荷载分布形式.为获得结构在柱瞬间失效条件下对应不同重力荷载水平的动力反应,可以采用对满跨重力荷载进行逐级增加,也可以采用仅对失柱损伤范围内的受损跨重力荷载进行逐级增加.那么不同的重力荷载分布形式对结构的动力反应影响有多大?3) 动力加载方式.传统的非线性动力分析方法需要对结构进行柱的瞬间移除,这对非线性分析技术要求较高,分析过程也较为复杂.而在Pushdown分析中,一般允许先移除柱,再进行加载[2].那么是否可以将这种先移除柱再施加荷载的动力加载方式引入到非线性动力分析中,来减少模拟结构瞬间失柱的困难?陈志恒[8]曾对柱失效时长对结构连续倒塌的非线性动力反应的影响进行了初步分析.本文在此基础上,选择按中国规范设计的一栋5层3跨钢筋混凝土框架结构作为研究对象,采用非线性动力分析方法,分别对框架柱失效时长、重力荷载分布形式和动力加载方式对结构动力反应影响进行了全面讨论.
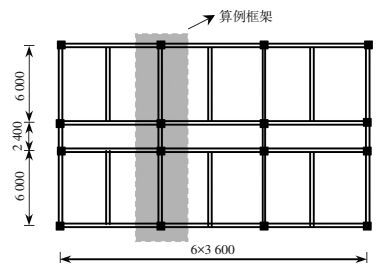
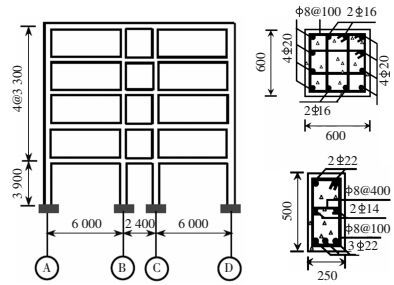
1 结构的设计和建模本文选取一栋5层3跨办公楼作为研究对象[8].结构平面布置见图 1,选取中间一榀框架作为研究对象,结构的立面布置及典型截面配筋,见图 2.
|
图 1 结构平面布置 (mm) Figure 1 Plan arrangement of the case structure (mm) |
|
图 2 结构立面布置及典型截面配筋 (mm) Figure 2 Elevation arrangement of the case structure and the reinforcement arrangement in typical sections (mm) |
本文采用OpenSees软件作为分析平台.具体的建模方式为:1) 材料模型:混凝土材料采用Concrete01模型,该材料模型采用了Scott拓展的Kent-Park混凝土本构关系[9],不考虑混凝土的受拉强度.为考虑箍筋约束对混凝土构件核心区混凝土抗压承载力的提升作用,采用Mander等[10]提出的箍筋约束混凝土的本构关系来计算Concrete01材料模型的控制点.钢筋材料采用Steel02模型,该材料是基于Menegotto等[11]提出的显式模型,可以考虑Bauschinger效应;2) 截面模型:混凝土截面采用纤维截面模型 (fiber section),该模型将构件纵向分割成若干段,以每一段中间某一截面的变形代表该段的变形.在截面上又划分成若干混凝土纤维和钢筋纤维,纤维单元的受力状态仅为一维,依据平截面假定来确定纤维的应变[12];3) 单元模型:混凝土梁-柱单元采用精细化塑性铰单元 (beam with hinges element),该模型考虑杆件端部形成一定长度的塑性铰,将塑性铰的截面划分为纤维截面,按照Gauss-Radau积分方法沿塑性铰长度积分来模拟构件和整体结构的非线性反应特点,而杆件中部的区段仍保持弹性,从而进行结构的非线性分析;4) 不考虑填充墙和楼板的影响;5) 二阶效应:采用旋转几何变换 (corotational transformation) 来考虑框架梁在大变形条件下的P-δ效应.
2 框架柱失效时长的影响根据GSA2003建议[1],在进行结构连续倒塌非线性动力分析时,柱失效时长应该小于结构自振周期的1/10.这一规定也从一个侧面说明了柱的瞬间失效只是一种理想假设.事实上,将柱从结构中移除相当于对结构在移除处施加一个反向荷载.而通过对结构在不同时间长度内施加反向荷载,即可考虑柱失效时长对结构连续倒塌动力分析结果的影响.为说明失效时长的概念,图 3给出了结构在移除柱前后的移柱上方节点的受力变化情况.由图 3可见,柱移除之前,结构保持受力平衡,柱端受力 (等效荷载)PE包括:弯矩M、轴力N和剪力V.柱移除之后,原由该柱承担的等效荷载PE(M、N和V) 将在ΔT时间段内退化为0,而ΔT即为失效时长.若ΔT无限接近于0,则可认为柱瞬间失效.随着ΔT的不断延长,移除柱的动力效应将逐渐减弱.

|
图 3 移除柱前后节点受力变化 Figure 3 Node force variation before and after column removal |
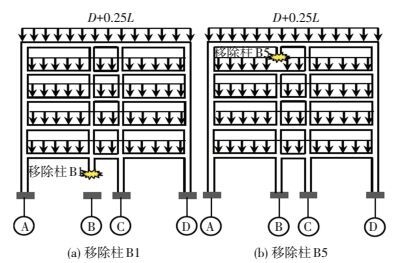
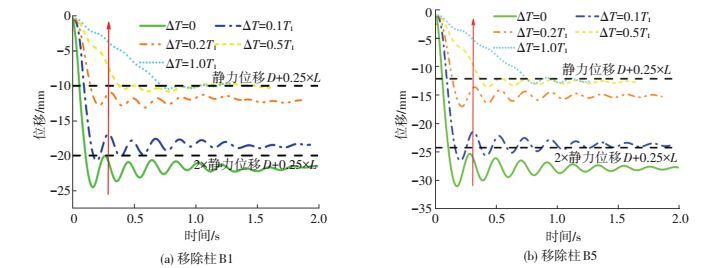
分别移除结构底层柱B1和顶层柱B5来进行结构连续倒塌的动力分析 (见图 4).结构施加的竖向均布荷载为D+0.25L[1].其中,D为恒荷载,L为活荷载.选取ΔT=0、0.1T1、0.2T1、0.5T1和1.0T1五种失效时长进行研究,结构竖向动力反应时程,见图 5.其中,T1=0.72 s为结构的基本自振周期.由图可见:随着失效时长的增加,柱瞬间失效所造成的结构动力效应不断减弱.在失效时长达到0.5T1时,柱瞬间失效所造成的动力效应已基本消失,结构将在静力分析的节点变形位置达到平衡.而当ΔT=0和0.1T1时,结构的动力效应相对比较显著,结构的节点平衡位移大约为结构在静力D+0.25L作用下节点位移的2倍.对比ΔT=0.0和0.1T1的分析结果,采用0.1T1作为柱失效时长并不会明显影响动力分析结果的精度.
|
图 4 柱移除位置 Figure 4 Locations of the removed column |
|
图 5 按不同失效时长移除柱所得的节点位移曲线 Figure 5 Node displacement curves due to different column removals withdifferent failure time |
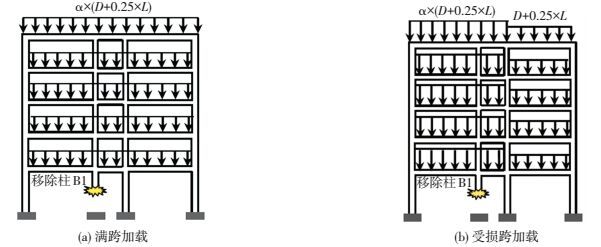
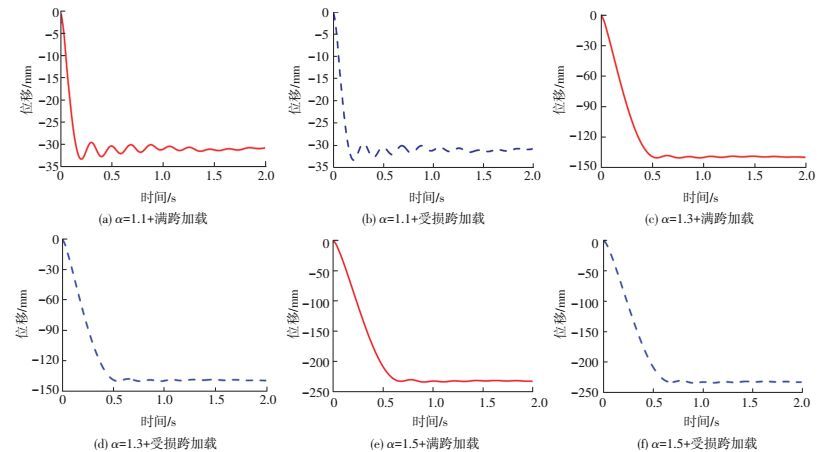
本文考虑受损跨和满跨两种重力荷载分布形式对动力反应的影响.图 6给出了两种重力荷载分布方式.由图可见,受损跨荷载分布只考虑移除柱上方受影响跨度的重力荷载增加,而其他未受影响跨度的重力荷载保持不变.满跨荷载分布是在结构各跨同时增加重力荷载.在结构柱B1瞬间失效后,分别采用受损跨和满跨荷载分布形式,重力荷载系数分别取:α=1.1、1.3和1.5,得到移除柱上方节点的非线性位移时程,见图 7.两种荷载分布形式作用下的节点动力反应几乎一致.这说明:移除某一柱所造成的影响范围是有限的,并不会在整个结构范围内进行扩展.
|
图 6 不同竖向荷载分布形式 Figure 6 Different vertical load distributions |
|
图 7 满跨加载和受损跨加载的节点位移曲线 Figure 7 Node displacement curves conditioned on the full-bay and damage-bay loads |
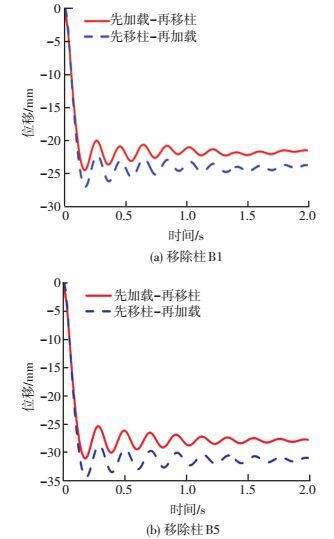
在进行Pushdown分析中,容许先移除柱再进行静力加载[1].这一加载方式忽略了结构在重力作用下的初始变形,大大简化了非线性分析的过程,从而有效降低了结构有限元分析的难度.受这一分析思想启发,本文在结构非线性动力分析中尝试采用先移除柱,再将重力荷载以动力荷载的形式施加到结构的分析策略.分别采用先移除柱再加载和先加载再移除柱两种动力加载方式,在结构柱B1和柱B5失效条件下,得到移柱上方节点的位移时程,见图 8.采用先移柱再加载的动力加载方式会在一定程度上放大抽柱对结构产生的动力效应.但是,这种放大作用十分有限,两种加载方式得到的结构动力反应较为接近.相比于先施加重力荷载再瞬间移除柱的分析方式,先移除柱再施加动力荷载的分析方式更利于程序实现,这也为近似模拟结构在柱瞬间失效条件下的动力反应提供了一种相对简便但具有较好精度的方法.
|
图 8 不同动力加载方式对应的节点位移曲线 Figure 8 Node displacement curves conditioned on different applying ways of dynamic loads |
1) 柱失效时长对结构的动力分析结果影响显著.随着失效时长的增加,移除构件对结构造成的动力效应逐渐减弱.当失效时长达到结构自振周期的0.5倍时,柱失效造成的动力效应基本消失.而当失效时长接近为0时,结构的动力效应最大.采用GSA2003建议的0.1T1作为失效时长,可以获得与柱瞬间失效相差不多的动力分析结果.
2) 满跨和受损跨重力荷载分布形式对非线性动力分析结果影响几乎可以忽略不计.换言之,柱瞬间失效对结构的影响范围是有限的,某一柱的损伤并不会造成初始损伤在整个结构范围内的传递.
3) 采用先移除柱再将重力荷载以动力形式进行施加的非线性动力分析过程会一定程度的放大结构的动力效应.但这种放大效应较为有限,这也为进行结构连续倒塌的动力分析提供了另一种较为容易实现的分析方法.
| [1] | General Services Administration (GSA). Progressive collapse analysis and design guidelines for new federal office buildings and major modernization projects[S]. Washington DC: GSA, United States, 2003. |
| [2] | Department of Defense (DoD). Design of structures to resist progressivecollapse[S]. Washington DC: DoD, 2005. |
| [3] |
中国工程建设标准化协会. 建筑结构抗倒塌设计规范: CECS 392—2010[S]. 北京: 中国计划出版社, 2015.
China Association for Engineering Construction Standardization. Code for anti-collapse design of building structures: CECS 392—2010[S]. Beijing: China Planning Press, 2015. |
| [4] | KAPIL K, SHERIF EI-TAWIL. Pushdown resistance as a measure of robustness in progressivecollapse analysis[J]. Engineering Structures, 2011, 33(9): 2653-2661. DOI: 10.1016/j.engstruct.2011.05.013 |
| [5] |
李易, 陆新征, 叶列平, 等. 基于Pushdown分析的RC框架抗连续倒塌承载力研究[J].
沈阳建筑大学学报 (自然科学版), 2011, 27(1): 10-19.
LI Yi, LU Xinzheng, YE Lieping, et al. Study on progressive-collapse resistance capacity of RCframe structures based on pushdown analysis[J]. Journal of Shenyang Jianzhu University (Natural Science), 2011, 27(1): 10-19. |
| [6] |
马高, 李惠, 欧进萍. 基于构件拆除法的RC框架结构动力反应和抗倒塌能力分析[J].
震灾防御技术, 2010, 5(1): 62-72.
MA Gao, LI Hui, OU Jinping. Dynamic response and collapse capacity analysis of RC frame buildings based on the element-removal method[J]. Technology for Earthquake Disaster Prevention, 2010, 5(1): 62-72. DOI: 10.11899/zzfy20100108 |
| [7] |
吕大刚, 李雁军, 陈志恒. 钢筋混凝土框架结构连续倒塌的竖向非线性动力分析[J].
土木建筑与环境工程, 2012, 34(Sl): 49-53.
LYU Dagang, LI Yanjun, CHEN Zhiheng. Progressive collapse analysis of RC frame using vertical nonlinear dynamic analysis. Journal of Civil[J]. Architectural & Environmental Engineering, 2012, 34(Sl): 49-53. |
| [8] |
陈志恒. 钢筋混凝土框架结构倒塌失效模式、风险与鲁棒性分析[D]. 哈尔滨: 哈尔滨工业大学, 2008.
CHEN Zhiheng. Collapse modes, risk and robustness analysis of RC frame structures[D]. Harbin: Harbin Institute of Technology, 2008. |
| [9] | SCOTT B D, PARK R, PRIESTLEY M J N. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates[J]. ACI Journal proceedings, 1982, 79(2): 13-27. |
| [10] | MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress-strain model for confined concrete[J]. ASCE Journal of Structural Engineering, 1998, 114(8): 1804-1826. DOI: 10.1061/(ASCE)0733-9445(1988)114:8(1804) |
| [11] | MENEGOTTO M, PINTO P E. Method of analysis of cyclically loaded RC plane frames including changes in geometry and non-elastic behavior of elements under normal force and bending[C]// Proceedings of IABSE Symposium on Resistance and Ultimate Deformability of Structures Acted on by Well-Defined Repeated Loads. Lisbon, Portugal: International Association for Bridge and Structural Engineering, 1973: 15-22. |
| [12] | SPACONE E, FILIPPOU F C, TAUCER F F. Fiber beam-column model for nonlinear analysis of R/C frames: part 1: formulation[J]. Earthquake Engineering and Structural Dynamics, 1996, 25(7): 711-725. DOI: 10.1002/(SICI)1096-9845(199607)25:7<711:AID-EQE576>3.0.CO;2-9 |
 2017, Vol. 49
2017, Vol. 49


