钢筋混凝土结构的梁柱节点单元[1],根据节点变形和受力机理,将节点从功能上区分为节点核心区剪切块的剪切变形、梁柱与核心区交界面的剪切变形和梁柱受力钢筋与核心区混凝土的粘结滑移三大功能组成部分,并分别用三组共13根一维弹簧来描述该三大组成部分的材料模型.由于该单元的组成方式不同于一般单元,因此,该节点单元被称为“超级单元”.其中,核心区剪切块假定受纯剪切作用,因此用一根弹簧描述剪力与剪切变形之间的关系;梁柱与核心区4个交界面剪力与剪切位移关系用4根弹簧描述;而位于节点两边的梁上下部钢筋以及位于节点上下的柱左右两边钢筋共用8根弹簧描述钢筋与核心区混凝土之间的粘结滑移关系.
对于超级单元核心区剪切块材料模型怎样建立,不同的学者有不同的主张.超级单元的建立者[1-2]根据MCFT理论[3],利用有限元方法计算核心区的剪力和剪切变形之间的关系.LaFave等[4]则依据试验统计资料,根据统计分析模型建立的经验公式确定该材料的物理关系.从而可知,超级单元中核心区的剪切材料模型怎样建立,对于超级单元的使用者来说是一个难点.
为了避免核心区剪切材料物理关系建立的困难,本文将超级单元的核心区用平面四节点单元代替,同时考虑梁柱钢筋与核心区混凝土的粘结滑移作用,建立一种新的基于平面4节点单元的梁柱节点单元,并在商业平台ABAQUS上开发了应用程序.新单元的核心区材料模型由钢筋和混凝土材料根据平面应力状态的MCFT理论[5]建立,不需要使用者提供额外的剪切与剪切变形关系,避免了使用超级单元时不易提供剪切物理关系的困难.本单元与超级单元一样,分析结构时,梁柱由一般梁柱单元模拟,因此,本单元的节点自由度与一般梁柱单元的节点自由度能够顺利衔接.通过循环荷载下钢筋混凝土内、边和角框架3个节点的试验结果数值分析,验证了本单元的有效性.
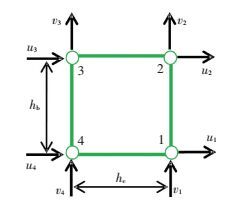
1 节点单元构成本单元由4个外节点和4个内节点组成,其中外节点的自由度为3个,与普通梁单元自由度一致,见图 1;而内节点自由度与普通平面应力单元的自由度一致,内节点自由度见图 2.图 1中,外部的数字代表外节点编号,内部的数字则代表内节点编号.

|
图 1 单元的节点和自由度 Figure 1 Nodes and degrees of freedom in the element |
|
图 2 节点核心区单元 Figure 2 Element of joint core |
考虑钢筋粘结滑移和梁柱与节点交界面裂缝影响,本节点单元将节点与梁柱交界面处截面,分成“节点截面”和“梁柱截面”(图 1),节点中钢筋与混凝土之间的粘结滑移关系由梁柱截面和节点截面上的自由度一起反映.
本节点的构成思想是:针对文献[1]超级单元中反映核心区剪切,改由平面四节点单元代替,而反映梁柱受力钢筋与混凝土粘结滑移的8根弹簧,以及节点与核心区交界面的4个剪切弹簧,本单元保留,即本单元由一个四节点平面单元组合8根粘结滑移弹簧和4根剪切弹簧而成.
由于内外节点的自由度不同,不利于在通用商业平台上进行二次开发,因此,本文将内节点的自由度“依附”到外节点上,形成一种“超自由度”形式,故不妨称本梁柱节点单元为“超自由度”单元.经过上述自由度依附之后,在数值表现上,本文的梁柱节点单元为:“单元具有4个节点,每个节点具有5个自由度”的单元几何构造.程序实现时,以单元的外节点作为单元节点,内节点按照图 1形式由程序内定形成.
超自由度单元的节点位移向量为
| $ \mathit{\boldsymbol{ \boldsymbol{\varDelta} = }}{\left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{D}}_1}}&{{\mathit{\boldsymbol{D}}_2}}&{{\mathit{\boldsymbol{D}}_3}}&{{\mathit{\boldsymbol{D}}_4}} \end{array}} \right\}^{\rm{T}}}, $ | (1) |
式中Di为i(i=1~4) 节点的超级自由度向量,以节点1为例:
| ${\mathit{\boldsymbol{D}}_1} = {\left\{ {\begin{array}{*{20}{c}} {{\mathit{\Delta }_1}} & {{\mathit{\Delta }_2}} & {{\mathit{\Delta }_3}} & {{u_1}} & {{v_1}} \end{array}} \right\}^{\rm{T}}}.$ | (2) |
式中前3个自由度Δ1、Δ2和Δ3属于外节点,后2个自由度u1和v1属于内节点,即内节点1的水平和竖向位移 (图 2),式 (1) 中其余3个节点的自由度向量依次类推.
超级自由度的实现方式,以通用商业平台ABAQUS为例,单元节点前13个自由度具有固定意义,如1至6自由度分别为X、Y和Z坐标方向的位移和转角.式 (2) 中前3个自由度正好对应1、2和6,而式 (2) 中后2个自由度可以采用14和15,对应的输入命令如下:
| $ \begin{array}{l} * \;{\rm{USER}}\;{\rm{ELEMENT}},NODES = 4,TYPE = U4, \cdots \cdots \\ 1,2,6,14,15 \end{array} $ |
内节点单元为普通的平面应力单元,见图 2.hb为节点的高度,也即梁高;hc为节点的宽度,即柱宽.下面分别从变形关系、平衡关系和物理关系来介绍本单元,并在该三大关系的基础上导出单元刚度矩阵和节点抗力向量.
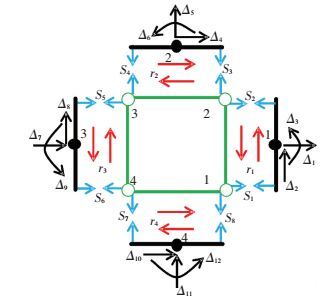
2 梁柱截面与节点截面变形关系节点截面与梁柱截面之间的变形关系见图 3,其中ri(i=1~4) 为剪切变形,Si(i=1~8) 为钢筋与混凝土之间的粘结滑移变形,该变形也就是模拟粘结滑移弹簧的伸长量.
|
图 3 两截面之间的位移关系 Figure 3 Displacement relationship between two sections |
显然,剪切变形与节点自由度之间有如下关系
| $ \left\{ \begin{array}{l} {r_1} = {\mathit{\Delta }_2} - \left( {{v_1} + {v_2}} \right)/2,\\ {r_2} = {\mathit{\Delta }_4} - \left( {{u_2} + {u_3}} \right)/2,\\ {r_3} = {\mathit{\Delta }_8} - \left( {{v_3} + {v_4}} \right)/2,\\ {r_4} = {\mathit{\Delta }_{10}} - \left( {{u_1} + {u_4}} \right)/2. \end{array} \right. $ | (3) |
假定fb和fc分别为梁上下钢筋间距和柱子两侧钢筋间距与截面高度的比值,即fbhb(hb见图 2) 为梁上下钢筋之间的间距[1].
令:αc=0.5hcfc、βc=(1+fc)/2、γc=(1-fc)/2,相应的αb,βb和γb仅是将式中下标c改为b即可,则弹簧伸长量与节点自由度有如下关系:
| $ \left\{ \begin{array}{l} {S_1} = {\mathit{\Delta }_1} + {{\rm{\alpha }}_{\rm{b}}}{\mathit{\Delta }_3} - {\beta _{\rm{b}}}{u_1} - {\gamma _{\rm{b}}}{u_2},\\ {S_2} = {\mathit{\Delta }_1} + {{\rm{\alpha }}_{\rm{b}}}{\mathit{\Delta }_3} - {\gamma _{\rm{b}}}{u_1} - {\beta _{\rm{b}}}{u_2},\\ {S_3} = {\mathit{\Delta }_5} + {{\rm{\alpha }}_{\rm{c}}}{\mathit{\Delta }_6} - {\beta _{\rm{c}}}{v_2} - {\gamma _{\rm{c}}}{v_3},\\ {S_4} = {\mathit{\Delta }_5} - {{\rm{\alpha }}_{\rm{c}}}{\mathit{\Delta }_6} - {\gamma _{\rm{c}}}{v_2} - {\beta _{\rm{c}}}{v_3},\\ {S_5} = - {\mathit{\Delta }_7} + {{\rm{\alpha }}_{\rm{b}}}{\mathit{\Delta }_9} + {\beta _{\rm{b}}}{u_3} + {\gamma _{\rm{b}}}{u_4},\\ {S_6} = - {\mathit{\Delta }_7} - {{\rm{\alpha }}_{\rm{b}}}{\mathit{\Delta }_9} + {\gamma _{\rm{b}}}{u_3} + {\beta _{\rm{b}}}{u_4},\\ {S_7} = - {\mathit{\Delta }_{11}} + {{\rm{\alpha }}_{\rm{c}}}{\mathit{\Delta }_{12}} + {\beta _{\rm{c}}}{v_4} + {\gamma _{\rm{c}}}{v_1},\\ {S_8} = - {\mathit{\Delta }_{11}} - {{\rm{\alpha }}_{\rm{c}}}{\mathit{\Delta }_{12}} + {\gamma _{\rm{c}}}{v_4} + {\beta _{\rm{c}}}{v_1}. \end{array} \right. $ | (4) |
单元的节点抗力向量为
| $ \mathit{\boldsymbol{F = }}{\left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{f}}_1}}&{{\mathit{\boldsymbol{f}}_2}}&{{\mathit{\boldsymbol{f}}_3}}&{{\mathit{\boldsymbol{f}}_4}} \end{array}} \right\}^{\rm{T}}}. $ | (5) |
式中:f1={F1 F2 F3 X1 Y1}T为对应节点1超级自由度向量D1的节点抗力向量,其余3个节点的抗力向量依次类推.Fi与图 3节点位移Δi相对应;Xi和Yi与图 2中节点位移ui和vi相对应;8根粘结滑移弹簧力用Pi表示,Pi与图 3弹簧伸长Si相对应;模拟截面剪切变形的4根弹簧力用Qi表示,Qi与图 3剪切位移ri相对应.
粘结滑移弹簧力与单元节点抗力之间的平衡关系为
| $ \left\{ \begin{array}{l} {F_1} = {P_1} + {P_2},\\ {F_3} = \left( {{P_1} - {P_2}} \right){h_{\rm{b}}}{f_{\rm{b}}}/2,\\ {F_5} = {P_3} + {P_4},\\ {F_6} = \left( {{P_3} - {P_4}} \right){h_{\rm{c}}}{f_{\rm{c}}}/2,\\ {F_7} = - {P_5} - {P_6},\\ {F_9} = \left( {{P_6} - {P_5}} \right){h_{\rm{b}}}{f_{\rm{b}}}/2,\\ {F_{11}} = - {P_7} - {P_8},\\ {F_{12}} = \left( {{P_8} - {P_7}} \right){h_{\rm{c}}}{f_{\rm{c}}}/2. \end{array} \right. $ | (6) |
截面剪切弹簧力与单元节点抗力之间的平衡关系为
| $ \left\{ \begin{array}{l} {F_2} = - \left( {{Y_1} + {Y_2}} \right) = {Q_1},\\ {F_4} = - \left( {{Y_2} + {Y_3}} \right) = {Q_2},\\ {F_8} = - \left( {{Y_3} + {Y_4}} \right) = {Q_3},\\ {F_{10}} = - \left( {{Y_1} + {Y_4}} \right) = {Q_4}, \end{array} \right. $ | (7) |
本节点存在4种材料的物理关系:(1) 平面单元的混凝土材料;(2) 平面单元内钢筋材料,包括节点内的箍筋和梁柱穿插于节点内的受力钢筋;(3) 梁柱受力钢筋与节点核心区内混凝土之间的粘结滑移;(4) 梁柱截面与节点截面之间的剪切变形物理关系.其中,(1) 和 (2) 中混凝土材料采用MCFT理论建立物理关系[3, 5],钢筋材料采用根据Ramberg-Osgood公式建立的滞回钢筋模型[3, 5],两种材料在商业平台ABAQUS上的UMAT接口程序已经过数值检验[5-6].而 (3) 中的粘结滑移物理关系,由于超级单元使用的粘结滑移关系[1-2]已经过OpenSees大量用户的检验,因此,在本节点上直接采用该材料模型.对于上述 (4) 变形关系[7],由于本文的重点不在于建立这样的剪切模型,因此,在本文的数值实现过程中假定该关系为线弹性的.
5 刚度矩阵图 2所示的平面单元刚度矩阵为
| $ {\mathit{\boldsymbol{K}}_i} = \sum\limits_{j = 1}^N {\sum\limits_{m = 1}^N {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{DB}}W\left( {{\xi _j}} \right)W\left( {{\eta _m}} \right)V/4} } . $ | (8) |
式中:N是高斯积分点数,W(ξj) 和W(ηm) 为高斯积分权重,ξj和ηm为高斯点的自然坐标值,V是节点的体积,D是根据MCFT理论得到的混凝土材料应力应变雅可比矩阵[5]和根据滞回钢筋模型得到的节点箍筋和梁柱受力钢筋材料应力应变雅可比矩阵[5],B是平面单元的应变矩阵,如式 (9) 所示.
| $ \mathit{\boldsymbol{B = }}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1}}&{{\mathit{\boldsymbol{B}}_2}}&{{\mathit{\boldsymbol{B}}_3}}&{{\mathit{\boldsymbol{B}}_4}} \end{array}} \right], $ | (9) |
式中
| $ {\mathit{\boldsymbol{B}}_1} = \frac{1}{2}\left[ {\begin{array}{*{20}{c}} {\left( {1 - \eta } \right)/{h_{\rm{c}}}}&0\\ 0&{ - \left( {1 + \xi } \right)/{h_{\rm{b}}}}\\ { - \left( {1 + \xi } \right)/{h_{\rm{b}}}}&{\left( {1 - \eta } \right)/{h_{\rm{c}}}} \end{array}} \right]. $ | (10) |
其余3个类推可得.式 (8) 建立的刚度矩阵为对应单元的内节点自由度部分,而单元的总刚度矩阵还要考虑8根粘结滑移弹簧和4根剪切弹簧引起的刚度.
粘结滑移弹簧刚度矩阵,以弹簧1为例,余者依次类推.将式 (4) 中弹簧1的位移S1写成矩阵形式,有:
| $ {S_1} = {\mathit{\boldsymbol{B}}_{{\rm{s}}1}}{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_{{\rm{s}}1}}, $ | (11) |
式中:Bs1=[1 αb -βb -γb],Δs1是{Δ1 Δ3 u1 u2}T.
此时弹簧的刚度记为Ds1,则其刚度矩阵为
| $ {\mathit{\boldsymbol{K}}_{{\rm{s}}1}} = \mathit{\boldsymbol{B}}_{{\rm{s}}1}^{\rm{T}}{D_{{\rm{s}}1}}{\mathit{\boldsymbol{B}}_{{\rm{s}}1}}. $ | (12) |
同理,将式 (3) 的剪切弹簧变形写成矩阵形式,以r1为例,则有:
| $ {r_1} = {\mathit{\boldsymbol{B}}_{{\rm{r}}1}}{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_{{\rm{r}}1}}, $ | (13) |
式中:Br1=[1 -0.5 -0.5],Δr1是{Δ2 v1 v2}T.
若剪切刚度记为Dr1,则其刚度矩阵为
| $ {\mathit{\boldsymbol{K}}_{{\rm{r}}1}} = \mathit{\boldsymbol{B}}_{{\rm{r}}1}^{\rm{T}}{D_{{\rm{r}}1}}{\mathit{\boldsymbol{B}}_{{\rm{r}}1}}. $ | (14) |
将式 (8)、(12) 和 (14) 组合,即可得到节点单元的总刚度矩阵.
6 节点抗力向量平面单元 (图 2) 在当前应力状态下的节点抗力向量为
| $ \mathit{\boldsymbol{X = }}\sum\limits_{j = 1}^N {\sum\limits_{m = 1}^N {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{\sigma }}W\left( {{\xi _j}} \right)W\left( {{\eta _m}} \right)V/4} } . $ | (15) |
式中:X={N1 N2 N3 N4}T,Ni即为{Xi Yi}T,σ为平面单元高斯点的应力向量.8根弹簧引起的节点抗力,仍然以弹簧1为例,由式 (4) 知,若弹簧1当前状态的弹簧力为P1,则其引起的节点抗力向量为
| $ {\mathit{\boldsymbol{F}}_{{\rm{s}}1}} = \mathit{\boldsymbol{B}}_{{\rm{s}}1}^{\rm{T}}{P_1}. $ | (16) |
式中:Fs1是{F1 F3 X1 X2}T,Bs1同式 (11).4根剪切变形弹簧引起的节点抗力向量,以r1为例则有:
| $ {\mathit{\boldsymbol{F}}_{{\rm{r}}1}} = \mathit{\boldsymbol{B}}_{{\rm{r}}1}^{\rm{T}}{Q_1}. $ | (17) |
式中:Fr1是{F2 Y1 Y2}T,而Q1为对应的剪力.组合式 (15)、(16) 和 (17) 即可得到总节点抗力向量.
7 力与位移关系非线性问题的有限元求解过程中,对于每个荷载增量步每次循环,都需要求解下式:
| $ \mathit{\boldsymbol{K}} \cdot \mathit{\boldsymbol{\delta = P}} - \mathit{\boldsymbol{F}}. $ | (18) |
式中:K即为由式 (8)、(12) 和 (14) 求得的当前循环步的单元刚度矩阵,δ为位移增量向量,P为当前增量步的总荷载向量,F为由式 (15)、(16) 和 (17) 求得的节点抗力向量.
8 验证本文选择内框架节点UNIT1[8]、边框架节点UNIT3[9]和角框架节点KJ5[10]的试验结果来验证单元的有效性.下列算例中,梁柱单元采用ABAQUS的B21梁单元,梁柱钢筋用rebar形式,即不考虑梁柱的钢筋与混凝土间粘结滑移[5-6].梁柱单元采用分层法,混凝土材料采用OpenSees中的concrete01模型,即忽略混凝土拉应力.钢筋的滞回模型采用Vecchio模型[5].
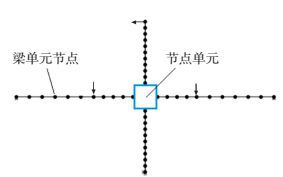
8.1 算例1-内框架节点UNIT1本算例[8]是超级单元在OpenSees平台上验证的算例,相关试验数据也可于OpenSees网站获得.分析中节点每边的梁柱都划分10个单元,其中梁上荷载作用点到节点之间分4个单元 (ABAQUS计算模型见图 4).
|
图 4 UNIT1分析模型 Figure 4 Analysis model of UNIT1 |
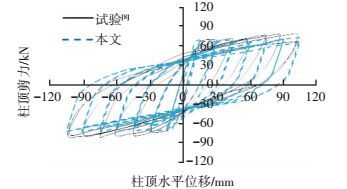
图 5给出UNIT1柱顶水平荷载和水平位移滞回曲线的试验[8]与本文分析结果对比.可以看出,本文提出的单元,在节点承载能力、滞回曲线的捏拢效果上,基本能够很好地描述试验结果.而其在cpu主频为2.5 GHz的intel i5内存8 G的笔记本电脑上“用户运算时间”为110.40 s,运算效率应该是令人非常满意的.
|
图 5 UNIT1试验与分析滞回曲线对比 Figure 5 Comparison of load-deflection responses for UNIT1 |
分析中梁和上下柱均分10个单元,图 6为梁端荷载与位移滞回曲线的试验[9]和本文分析结果.

|
图 6 UNIT3试验与分析滞回曲线对比 Figure 6 Comparison of load-deflection responses for UNIT3 |
从图 6可看出,在承载能力、初始刚度和捏拢效果上,本文方法都基本能够准确描述,说明本单元在边节点上有着比较好的表现.
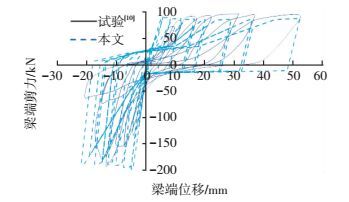
8.3 算例3-角框架节点KJ5分析中梁柱均分10个单元,原试验曲线是梁柱交界面上,梁截面弯矩与柱偏转角之间的滞回曲线[10],本文将该滞回曲线转换为梁加载端剪力与轴向位移之间的滞回曲线.梁端受拉力时,角框架变形为“张开”,对应滞回曲线上的正位移与正剪力;梁端受压力时,角框架变形为“闭合”,对应滞回曲线上的负位移与负剪力.滞回曲线的本文方法分析结果和试验结果对比见图 7.
|
图 7 KJ5试验与分析滞回曲线对比 Figure 7 Comparison of load-deflection responses for KJ5 |
从图 7可看出,在承载能力上,本文方法基本能准确描述.“张开”变形的强度描述基本准确,而在“闭合”变形后期加载时,结构强度严重退化,本文方法虽有反映,但退化程度与实际差距较大.
9 结语本文将钢筋混凝土梁柱节点单元的内节点自由度“依附”到外节点上形成一种“超自由度”模式的单元,通过编制单元的UEL程序将其移植到ABAQUS通用分析平台上,使得循环荷载作用下的钢筋混凝土框架结构的非线性分析可以真正在通用数值分析平台得以进行,为钢筋混凝土框架结构在通用平台上进行动力荷载作用下的非线性分析打下了坚实基础.通过对钢筋混凝土结构内、边和角框架节点3个梁柱节点模型试验的算例分析,也验证了本文“超自由度”节点单元的有效性.
| [1] | MITRA N, LOWES L N. Evaluation, calibration, and verification of a reinforced concrete beam-column joint model[J]. Journal of Structural Engineering, ASCE, 2007, 133(1): 105-120. DOI: 10.1061/(ASCE)0733-9445(2007)133:1(105) |
| [2] | LOWES L N, ALTOONTASH A. Modeling reinforced concrete beam-column joints subjected to cyclic loading[J]. Journal of Structural Engineering, ASCE, 2003, 129(12): 1686-1697. DOI: 10.1061/(ASCE)0733-9445(2003)129:12(1686) |
| [3] | VECCHIO F J, COLLINS M P. The modified compression field theory for reinforced concrete elements subjected to shear[J]. ACI Structural Journal, 1986, 83(2): 219-231. |
| [4] | LAFAVE J M, KIM J R. Joint shear behavior prediction for RC beam-column connections[J]. International Journal of Concrete Structures and Materials, 2011, 5(1): 57-64. DOI: 10.4334/IJCSM.2011.5.1.057 |
| [5] |
方自虎, 谢强, 周尧, 等. 循环荷载下MCFT混凝土结构模型[J].
地震工程与工程振动, 2015, 35(3): 73-78.
FANG Zihu, XIE Qiang, ZHOU Yao, et al. MCFT model of concrete structures subjected to cyclic loading[J]. Earthquake Engineering and Engineering Dynamics, 2015, 35(3): 73-78. DOI: 10.13197/j.eeev.2015.03.073.fangzh.009 |
| [6] |
方自虎, 简旭阳, 周尧, 等. 考虑屈曲的钢筋滞回模型[J].
武汉大学学报, 2016, 49(2): 254-258.
FANGZihu, JIAN Xuyang, ZHOU Yao, et al. Hysteretic model of reinforced bar considering buckling[J]. Engineering Joural of Wuhan University, 2016, 49(2): 254-258. |
| [7] | SHIOHARA H. New model for shear failure of RC interior beam-column connections[J]. Journal of Structural Engineering, ASCE, 2001, 127(2): 152-160. DOI: 10.1061/(ASCE)0733-9445(2001)127:2(152) |
| [8] | PARK R, RUITONG D. A comparison of the behavior of reinforced concrete beam-column joints designed for ductility and limited ductility[J]. Bulletin of the New Zealand National Society of Earthquake Engineering, 1988, 21(4): 255-278. |
| [9] | PARK R, MILBURN J R. Comparison of recent New Zealand and United States seismic design provisions for reinforced concrete beam-column joints and test results from four units designed according to the New Zealand code[J]. Bulletin of the New Zealand national society for earthquake engineering, 1983, 16(1): 3-24. |
| [10] | ANGELAKOS B. The behavior of reinforced concrete knee joints under earthquake loads[D]. Toronto: University of Toronto, 1999. |
 2017, Vol. 49
2017, Vol. 49


