2. 哈尔滨工业大学 土木工程学院, 哈尔滨 150090
2. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China
钢桁架具有自重轻,能够实现大柱网、大跨度的工艺要求,以及运输和拼接方便等优点,这使得该结构形式已较多的应用于各类工业与民用建筑中.中国现行钢结构规范[1]仅规定了实腹梁整体稳定的计算方法,但所给出的稳定系数公式未必适合于钢桁架结构.
2000年,Rasmussen[2]提出了桁架极限承载力可以采用塑性铰法,随荷载增加,当桁架中某根杆件的内力组合达到屈服时,就在该杆件截面内引进一个塑性铰,继续加载至结构已形成足够多的塑性铰后,整个结构被破坏即认为荷载已经达到极限荷载;2005年,唐柏鉴等[3]对空间桁架梁进行了多个算例的分析比较,发现空间桁架梁具有很好的整体稳定性;2010年,Iwichi等[4-6]研究了面外支撑刚度对桁架屈曲临界荷载的影响,分析得出桁架的临界屈曲荷载取决于面外支撑的刚度和间距.空间桁架不仅竖向刚度较大,平面外刚度也较高,且整体稳定问题并不突出[7-9].而平面桁架由于跨度大、截面抗扭能力差、受压弦杆的面外长细比大等特点,容易发生整体弯扭失稳,尤其是在面外没有足够支撑的情况下.
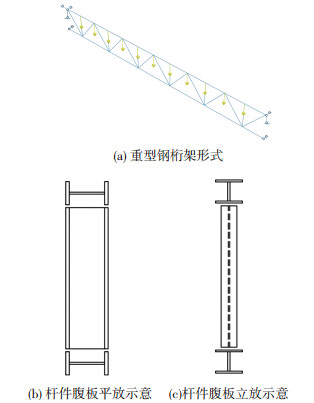
重型钢桁架是指荷载、跨度、截面高度均较大,且杆件通常使用H形或箱形等型钢构成的桁架,节点通常刚性连接.桁架上弦杆件沿纵向轴力不等,并受到腹杆和下弦杆的面外转动约束,整体稳定问题复杂.本文将从钢材型号、侧向支撑的数量和刚度、荷载作用位置、高跨比等几个方面研究特定参数下桁架的整体稳定性,并提出钢桁架不需考虑稳定问题的条件以及整体稳定系数的表达式.
1 重型钢桁架简介及有限元模型建立采用ABAQUS有限元程序建模时采用平行弦桁架形式,跨度为30 m,并选择了三类弦杆截面 (截面尺寸见表 1) 及四类高跨比 (1/15、1/10、1/8、1/6).由于调整上弦杆面外长细比时需要维持其截面面积不变,而改变截面的翼缘和腹板的宽度和厚度,因此表 1中仅给出了杆件截面面积.桁架杆件采用细分的梁单元 (B31),每个单元长度不超过30 cm,足以保证结果的准确性.节点为刚接,上弦的一端为固定铰支座,另一端为滑动铰支座,下弦两端支座仅约束面外位移.荷载以集中力形式作用在桁架弦杆与腹杆相交的节点上,各集中力数值相等,非线性分析时等幅增加.钢材采用Q345B,弹性模量2.06×105 MPa,泊松比0.3,密度7 850 kg/m3.采用双线性等向强化模型,本构关系为理想的弹塑性.高跨比为1/10的有限元模型见图 1.
|
图 1 高跨比为1/10的有限元模型 Figure 1 FE model for truss with depth-span ratio 1/10 |
| 表 1 模型杆件截面积 Table 1 Sectional area of truss membersmm2 |
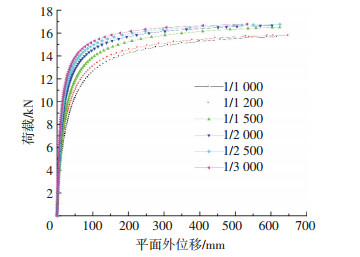
非线性分析当中,通常将线性屈曲分析得到的一阶屈曲模态作为初始几何缺陷.图 2表示的是初始几何缺陷幅值分别取跨度的1/1 000、1/1 200、1/1 500、1/2 000、1/2 500、1/3 000时对桁架平面外稳定承载力的影响,可见极限承载力随着缺陷幅值的减小逐渐增大,直到缺陷幅值小于跨度的1/2 500时,极限承载力将不再发生变化.中国《钢结构施工质量验收规范》[10]中对桁架侧向弯曲矢高允许偏差的规定为跨度的1/1 000,且不应大于10 mm.综合考虑有限元分析的结果与规范的规定,初始几何缺陷幅值取为L/3 000=10 mm.
|
图 2 初始几何缺陷对稳定承载力的影响 Figure 2 Influence of initial geometric imperfections on buckling capacity |
定义上弦杆面外长细比λ=l/iy,其中l为侧向支承点间距,无侧向支承点时取跨度,iy为上弦杆面外回转半径.桁架的稳定系数为
| $ {\varphi _{\rm{b}}} = \frac{{{M_x}}}{{{W_x}f}}, $ | (1) |
式中:Wx为抵抗矩,
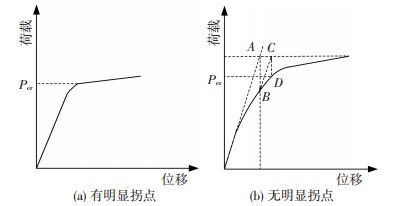
结构失稳是指在荷载幅值增加的过程中,会发生“增加微小的荷载幅值导致结构变形突然增大”,将此时对应的荷载定义为临界荷载.通过研究钢桁架非线性荷载-位移全程曲线发现两种不同模式,模式一有明显的拐点,该种模式比较容易确定临界荷载,见图 3(a);模式二没有明显的拐点,对于该模式采用几何作图法[11]得到临界荷载Pcr,见图 3(b),即:从初始切线与极限承载力的交点A向下作垂线,与荷载位移曲线交于B点,从B点以初始刚度作割线与极限承载力交于C点,从C点向下再作垂线与荷载位移曲线的交点D定义为临界荷载.
|
图 3 稳定承载力的确定方法 Figure 3 Methods for determining buckling capacity |
在同一类钢桁架中 (桁架杆件截面积一定),通过改变截面翼缘和腹板厚度、腹板的放置形式 (腹板平放和立放)、以及侧向支撑的个数来获得不同的面外长细比,进而研究上弦杆面外长细比对桁架整体稳定系数的影响.
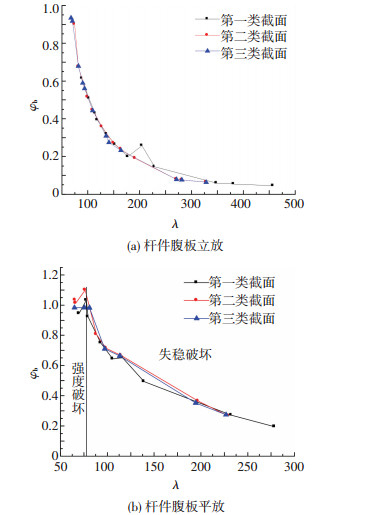
高跨比为1/10、不同侧撑个数的钢桁架的失稳模式见图 4,均为平面外失稳.通过图 5所示的有限元模拟结果可以发现,上弦杆的面外长细比是影响稳定系数的重要因素,长细比越小,稳定系数增大的速率越快.但当长细比减小到一定值时,稳定系数将逐渐趋于恒定值1.0,此时钢桁架不再出现面外失稳,而呈现强度破坏.将此时的长细比定义为临界长细比,作为钢桁架失稳破坏与强度破坏的分界 (图 5(b)).高跨比为其它他取值时,稳定系数与长细比的关系规律与高跨比1/10时一致,不再赘述.

|
图 4 高跨比1/10的桁架失稳形式 Figure 4 Buckling modes for truss with depth-span ratio 1/10 |
|
图 5 高跨比为1/10的三类截面稳定系数与长细比的关系曲线 Figure 5 Relationship between stability coefficient and slenderness ratio for trusses with depth-span ratio 1/10 |
通过图 5中三类截面桁架稳定系数与长细比的关系还可以发现,在长细比相同时,无论桁架杆件腹板立放还是平放,三类截面对应的稳定系数基本一致,从而可认为上下弦杆截面相等时,弦杆截面面积的大小对钢桁架的稳定系数没有影响.
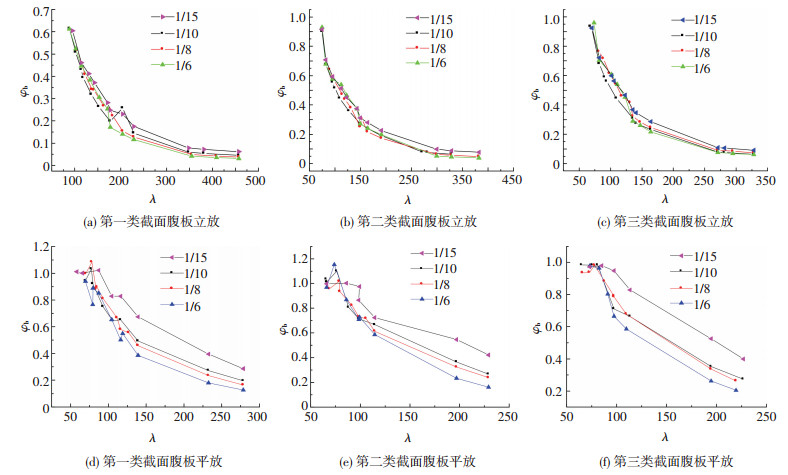
2.3 高跨比对稳定系数的影响图 6给出了不同高跨比时稳定系数与长细比的关系,可发现在同一类截面中,高跨比对钢桁架腹板立放时的稳定系数几乎无影响,而对钢桁架腹板平放时的稳定系数影响稍大.原因是:通过调节上弦杆的截面尺寸和腹板的放置形式使得上弦杆面外刚度逐渐增大,当上弦杆腹板由立放变为平放时,构造要求腹杆的腹板也一同转为平放,从而导致腹杆的面外刚度突然增大,对上弦杆面外变形约束能力也增大很多.因此,当桁架杆件腹板平放时,有必要对稳定系数进行修正.
|
图 6 不同高跨比的桁架稳定系数与长细比关系 Figure 6 Relationship between stability coefficient and slenderness ratio for trusses with different depth-span ratios |
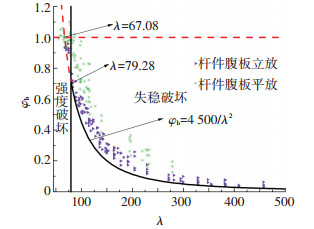
将不同高跨比、不同截面面积的钢桁架稳定系数与长细比的关系统一整理在图 7中,大量算例数据点呈现出了明显规律.出于工程设计中的保守考虑,取其下包络线,得到了稳定系数与上弦杆面外长细比的关系公式:
| $ {\varphi _{\rm{b}}} = \frac{{4500}}{{{\lambda ^2}}}. $ | (2) |
|
图 7 Q345钢的钢桁架稳定系数与长细比关系 Figure 7 Stability coefficients for trusses with Q345 steel |
该函数曲线分为实线和虚线两部分,分界处为λ=79.28,该值为桁架发生失稳破坏的最小值.为了方便设计且使钢桁架的强度破坏和失稳破坏的分界点有更充分的安全储备,将式 (2) 函数曲线与φb=1.0的交点 (λ=67.08) 定义为稳定与强度破坏的临界点,λ≤67.08时不再需要验算稳定.
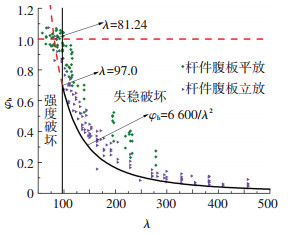
3 稳定系数的修正 3.1 考虑钢材强度对稳定系数的修正上一节研究Q345钢的钢桁架的稳定系数时,通过对大量算例进行有限元分析,最终得到了稳定系数的包络曲线.对于Q235钢桁架结构采用同样研究方法,得到的稳定系数见图 8,同样取其下包络线为式 (3),不需验算桁架稳定的条件为λ≤81.24.
| $ {\varphi _{\rm{b}}} = \frac{{6600}}{{{\lambda ^2}}}. $ | (3) |
|
图 8 Q235钢的钢桁架稳定系数与长细比关系 Figure 8 Stability coefficients for trusses with Q235 steel |
可发现式 (2) 的系数和不需验算稳定性的条件与式 (3) 存在如下关系:4 500≈6 600×(235/345),67.08≈81.24×(235/345)1/2.这种规律正好与实腹梁稳定系数考虑钢号调整的方法一致,因此,对于Q235钢和Q345钢可以将稳定系数统一表达为
| $ {\varphi _{\rm{b}}} = \frac{{6600}}{{{\lambda ^2}}} \cdot \frac{{235}}{{{f_{\rm{y}}}}},\;\;\lambda > 81.24\sqrt {\frac{{235}}{{{f_{\rm{y}}}}}} . $ | (4) |
仍以Q345钢材的桁架为研究对象,保持上弦杆截面不变,通过改变下弦杆截面面积使得钢桁架上、下弦截面积不等,来研究稳定系数的变化规律.有限元模型的截面见表 2.
| 表 2 有限元模型的弦杆截面改变形式 Table 2 Cross section for chord members |
上、下弦杆件规格不同决定了上、下弦杆件面外惯性矩的不同,为了表达这种差异,引入惯性矩比例系数α,其表达式为
| $ \alpha = \frac{{{I_1}}}{{{I_1} + {I_2}}}, $ | (5) |
式中I1、I2分别为上、下弦杆面外惯性矩.通过计算结果发现,在同一种长细比时,稳定系数与惯性矩比例系数α呈现出线性的关系,为了找到其斜率,引入截面不对称系数ηb,令:
| $ \eta ' = {\varphi _{\rm{b}}}/\left( {\frac{{4500}}{{{\lambda ^2}}}} \right). $ | (6) |
将特定长细比、高跨比下的每个η′与α的关系汇总于图 9,可以发现这些曲线有着共同的斜率0.4,用直线η′=0.4α+k来表示这种关系.当上下弦截面面积相等 (即α=0.5) 时η′=1,从而得到k=0.8,所以η′=1+0.4(α-0.5).令截面不对称系数ηb=0.4(α-0.5) 时,得到图 10,可以发现修正后的稳定系数能够很好地包络住所有计算结果.最终得到在钢材型号为Q345、上下弦截面面积不等时的钢桁架的稳定系数公式为
| $ {\varphi _{\rm{b}}} = \frac{{4500}}{{{\lambda ^2}}}\left( {1 + {\eta _{\rm{b}}}} \right), $ | (7) |

|
图 9 η′与惯性矩比例系数的关系曲线 Figure 9 Relationship between coefficient η′ and α |

|
图 10 上下弦截面不等时稳定系数公式验证 Figure 10 Stability coefficients for trusses with unequal chords |
式中ηb=0.4α-0.5, α≥0.5.
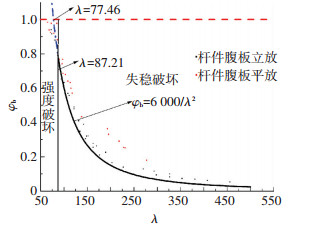
3.3 考虑荷载作用位置对稳定系数的修正由于杆件腹板立放时高跨比对稳定系数几乎无影响,但杆件腹板平放时,高跨比越大,钢桁架的稳定系数越小.因此在研究荷载作用位置对稳定系数的影响时选用稳定系数最小的情况,即模型高跨比为1/6.得到荷载作用于下弦节点时Q345钢桁架的计算结果见图 11.
|
图 11 荷载作用在下弦时的稳定系数 Figure 11 Stability coefficients with loading on joints of bottom chords |
给出此时稳定系数的包络公式:
| $ {\varphi _{\rm{b}}} = \frac{{6000}}{{{\lambda ^2}}},\;\;\;\lambda > 77.46. $ | (8) |
定义等效临界弯矩系数βb,使得
| $ {\varphi _{\rm{b}}} = {\beta _{\rm{b}}}\frac{{4500}}{{{\lambda ^2}}}\left( {1 + {\eta _{\rm{b}}}} \right), $ | (9) |
式中:当荷载作用于上弦杆时,βb=1;当荷载作用于下弦杆时,βb=1.33.不需验算稳定性的条件由λ≤67.08扩大为λ≤77.46,使用时出于安全考虑可以维持此条件不变.
3.4 考虑高跨比对稳定系数的修正由于桁架杆件的腹板平放时高跨比对稳定系数的影响较大,因此在桁架杆件腹板平放时有必要研究高跨比对稳定系数的影响.定义:
| $ \xi = {\varphi _{\rm{b}}}/\left( {\frac{{4500}}{{{\lambda ^2}}}} \right). $ | (10) |
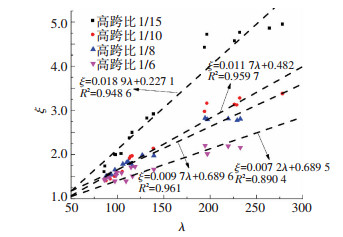
通过对ξ和长细比进行拟合,见图 12,发现ξ与长细比λ基本呈线性关系,且各拟合曲线的斜率与高跨比存在明显的反比关系:即0.018 9:0.011 7:0.009 7:0.007 2≈15:10:8:6.因此,ξ与λ关系曲线的斜率可统一表达为K/(h/L),其中K可取为4条直线计算结果的平均值0.012.由于图 12中4条拟合直线的常数项均较小且比较接近,近似统一取为恒定值0.5.故:
| $ \xi = \frac{{0.012}}{{h/L}}\lambda + 0.5, $ | (11) |
|
图 12 ξ与长细比的关系曲线 Figure 12 Relationship between coefficient ξ and slenderness ratio |
式中h/L为桁架高跨比.这样杆件腹板平放时Q345钢材桁架的稳定系数为
| $ {\varphi _{\rm{b}}} = \frac{{4500}}{{{\lambda ^2}}}\xi . $ | (12) |
考虑钢材屈服点、上下弦截面积不等、荷载作用位置以及高跨比等因素的影响,得到修正后的稳定系数公式为
| $ {\varphi _{\rm{b}}} = {\beta _{\rm{b}}}\frac{{6600}}{{{\lambda ^2}}}\xi \left( {1 + {\eta _{\rm{b}}}} \right)\frac{{235}}{{{f_{\rm{y}}}}} \le 1, $ | (13) |
式中:当荷载作用于上弦杆时βb=1,作用于下弦杆时βb=1.33;钢桁架杆件腹板立放时ξ=1,杆件腹板平放时
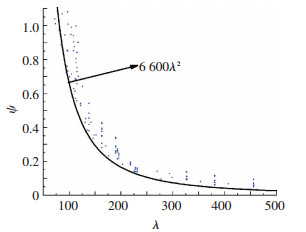
令ψ=φb/[βbξ(1+ηb)(235/fy)],将所有不同参数组合下模型稳定系数计算结果转化为ψ,观察ψ与曲线6 600/λ2的关系 (图 13).发现曲线6 600/λ2几乎包络住所有计算结果,且包络效果极好,从而验证式 (13) 合理.
|
图 13 通过参数ψ对稳定系数的综合验证 Figure 13 Stability coefficient verification using ψ |
1) 钢桁架的稳定系数与面外长细比呈现负相关的关系,并且长细比越小,稳定系数增大的越快,但当长细比减小到一定值时,稳定系数将逐渐趋于恒定值1.0,此时桁架受强度控制,并据此得到了不需考虑钢桁架整体稳定的条件.
2) 弦杆截面积对钢桁架的稳定系数没有影响.在杆件腹板平放时,高跨比越小,钢桁架的稳定系数越高,但杆件腹板立放时高跨比对稳定系数的影响不明显.
3) 增强上弦杆使上下弦杆截面不相等时,以及荷载由作用于上弦变为作用于下弦时,均将提高稳定系数.
4) 通过关键参数的影响分析,得到了H型钢杆件构成的重型桁架整体稳定系数计算公式,具有足够安全性,也便于工程应用.
| [1] |
钢结构设计规范: GB 50017—2003. [S]. 北京: 中国计划出版社, 2003.
Code for design of steel structures: GB 50017—2003[S]. Beijing: China Planning Press, 2003. |
| [2] | RASMUSSEN K J R. Recent research on stainless steel tubular structures[J]. Journal of Constructional Steel Research, 2000, 54(1): 75-88. DOI: 10.1016/S0143-974X(99)00052-8 |
| [3] |
唐柏鉴, 沈之容, 李一松. 空间桁架梁的研究与设计[J].
钢结构, 2005, 20(3): 49-51.
TANG Baijian, SHEN Zhirong, LI Yisong. Research and design of spatial truss beam[J]. Steel Construction, 2005, 20(3): 49-51. |
| [4] | IWICKI P. Stability of trusses with linear elastic side-supports[J]. Thin-Walled Structures, 2007, 45(10/11): 849-854. DOI: 10.1016/j.tws.2007.08.005 |
| [5] | IWICKI P. Sensitivity analysis of critical forces of trusses with side bracing[J]. Journal of Constructional Steel Research, 2010, 66(7): 923-930. DOI: 10.1016/j.jcsr.2010.02.004 |
| [6] | IWICKI P, KRAJEWSKI M. 3D buckling analysis of a truss with horizontal braces[J]. Mechanics and Mechanical Engineering, 2013, 17(1): 49-58. DOI: 10.1016/S0045-7949(97)00001-1 |
| [7] |
郭彦林, 郭宇飞, 盛和太. 钢管桁架拱的稳定性能及应用[J].
空间结构, 2008, 14(4): 41-49.
GUO Yanlin, GUO Yufei, SHENG Hetai. Stability behavior and application of truss-arch[J]. Spatial Structures, 2008, 14(4): 41-49. |
| [8] | NAZMY A S. Stability and load-carrying capacity of three-dimensional long-span steel arch bridges[J]. Computers & Structures, 1997, 65(6): 857-868. DOI: 10.1016/S0045-7949(97)00001-1 |
| [9] |
蒋沧如, 章东强, 袁健. 大跨度方钢管空间桁架结构的稳定性分析[J].
空间结构, 2009, 15(4): 56-59.
JIANG Cangru, ZHANG Dongqiang, YUAN Jian. Stability analysis of long-span spatial truss structure with square steel tube[J]. SpatialStructures, 2009, 15(4): 56-59. |
| [10] |
钢结构工程施工质量验收规范: GB 50205—2001[S]. 北京: 中国计划出版社, 2002.
Code for acceptance of construction quality of steel structures:GB 50205—2001[S]. Beijing: China Planning Press, 2002. |
| [11] | PARK R. Ductility evaluation from laboratory and analytical testing[C]// Proceedings of Ninth World Conference on Earthquake Engineering. Tokyo, Kyoto, Japan:[s.n.], 1988, Ⅷ: 605-616. |
 2017, Vol. 49
2017, Vol. 49


