组成冷弯薄壁型钢的板件宽而薄易发生局部屈曲.另一方面,由于板件的薄膜效应,只要构件整体不发生破坏,板件的局部屈曲并不会使构件的承载力立即丧失,且它还具有较高的屈曲后强度[1].因此,冷弯型钢结构设计不仅允许板件出现局部屈曲,而且还利用板件的屈曲后强度.
目前,各国在冷弯薄壁型钢结构的承载力设计中大多采用有效宽度法,如澳大利亚规范[2]、美国规范[3]等.该方法建立在单板的研究成果上,没有考虑整个截面中板件的相关性,即板组效应.相关研究表明[4-5],板组效应对冷弯薄壁型钢构件的承载力具有重要影响,但是如何考虑这种效应,国内外至今还未有统一认识.
为了计及板组效应对构件承载力的影响,部分学者从纯理论分析的角度入手,Rhodes等[6]通过理论分析建立了板组的屈曲后理论,并对槽型截面的屈曲后强度进行了研究.周绪红等[7-8]提出了求解板组屈曲后理论的半能量法,并对卷边槽型截面的屈曲后性能进行了研究.然而,由于纯理论的分析较为复杂,一般很难应用于指导设计实践,另一部分学者则从设计的角度出发,Schafer[9]在大量试验研究和理论分析的基础上,将柱子曲线的概念拓展应用于计算冷弯薄壁型钢构件的局部屈曲和畸变屈曲承载力,提出了冷弯薄壁型钢结构设计的直接强度法 (DSM).DSM通过板组的弹性相关屈曲来考虑板组效应对构件承载力的影响,这种线弹性分析方法避免了传统板组屈曲后理论的非线性运算,为相关设计人员提供了便利.随着DSM的发展和应用,各国学者对冷弯薄壁C形受压构件的板组弹性相关屈曲进行了大量研究[10-12],但大多针对板组畸变屈曲[10.12],对于板组局部屈曲的研究很少,已有临界荷载计算公式也多是半经验公式[11],其精度取决于回归分析时所选的参数范围,不便于应用,在一定程度上阻碍了DSM的发展与应用.
本文对薄壁受压C形截面的板组局部屈曲进行理论研究,推导了考虑板组效应的薄壁受压C形截面局部屈曲荷载解析解,通过有限条法对其进行验证.通过将本文解析解引入直接强度法,提出考虑板组效应的冷弯薄壁C形受压构件的局部屈曲承载力设计方法.
1 板件的局部屈曲相关性由于板组效应,截面中不同板件会同时发生屈曲,但这些板件发生屈曲的趋势却不同,通常最先具有这种趋势的板件决定着相邻板件间的约束关系,因而有必要了解截面中各板件屈曲的趋势.
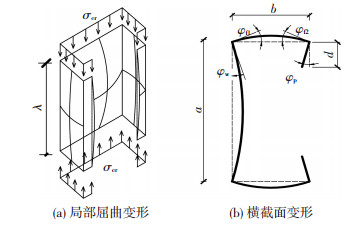
1.1 板件的强弱当C形受压构件发生局部屈曲时,取出一个半波长的柱段,如图 1(a)所示,相应的横截面变形,如图 1(b)所示.腹板、翼缘、卷边宽度分别为a、b和d,λ是构件纵向的一个半波长度.此时,截面具有如下特征[1, 4]:楞线保持挺直;相邻板件的交角不变.
|
图 1 冷弯薄壁C形截面局部屈曲变形 Figure 1 Local buckling deformation of cold-formed thin-walled C-sections |
如果腹板、翼缘和卷边互不约束,则临界荷载为[1]
| $ {\sigma _{{\rm{cr}}}} = k\frac{{{\pi ^2}E}}{{12\left( {1 - {\nu ^2}} \right)}}{\left( {\frac{t}{a}} \right)^2}, $ | (1) |
式中:腹板、翼缘和卷边的稳定系数k分别为4、4和0.43,t为板厚,a为板宽,E为弹性模量,ν为泊松比.
根据式 (1),如果各板件满足下列尺寸关系,则会同时发生屈曲.
| $ a = b = 3.05d. $ | (2) |
由式 (2) 可知:1) 当a>b且a>3.05d时,腹板的临界应力最小,它最先趋于屈曲;2) 当b>a且b>3.05d时,翼缘的临界应力最小,它最先趋于屈曲;3) 当a < 3.05d且b < 3.05d时,卷边的临界应力最小,它最先趋于屈曲.
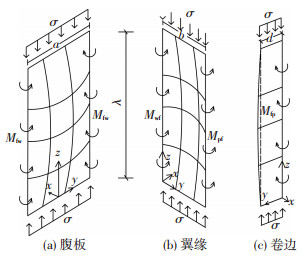
1.2 板件的相关作用为研究板件的相关作用,以腹板最先趋于屈曲为例,将图 1中腹板、翼缘和卷边拆分为以相关作用联系的3个分离体,如图 2所示 (Mwf、Mfw、Mpf和Mfp分别为腹板对翼缘、翼缘对腹板、卷边对翼缘和翼缘对卷边的约束弯矩).
|
注:Mfp当卷边受到翼缘约束时方向相反 图 2 板件分离体 Figure 2 Isolated plates |
由图 2知,如果腹板发生屈曲,必然会受到翼缘约束弯矩Mwf的牵制使其屈曲推迟,而翼缘则会受到腹板约束反力Mfw的作用使其提前屈曲.同理,翼缘与卷边间弯矩Mfp和Mpf会使弱者受到约束,强者受到牵制.最终,随着荷载不断增大,直至丧失稳定承载力,各板件会在相关作用的影响下同时发生屈曲.
综上所述,冷弯薄壁C形截面局部屈曲时,各板件间存在相关作用,这种作用以约束弯矩的形式使不同板件同时屈曲.因此,精确计算冷弯薄壁C形截面局部屈曲临界荷载时,必须考虑板件间的相关作用.
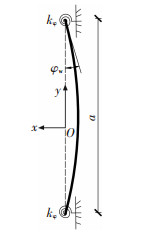
2 简化计算模型中国冷弯薄壁C形截面规格[13]的腹板高度a均大于翼缘宽度b且不小于3.05倍的卷边宽度d,即腹板为薄弱板件.当卷边对翼缘充分加劲时,截面的局部失稳形式为局部屈曲,此时各板件间的相关作用见图 2.取腹板分离体为分析简图,并以刚度为kφ的转动约束弹簧表述翼缘和卷边对腹板的共同约束作用,见图 3.简图的坐标轴原点位于形心处,z轴垂直纸面向外.
|
图 3 简化计算模型 Figure 3 The simplified calculation model |
分析模型的总势能V由弯曲应变能V1、转动弹簧的弹性势能V2以及外力势能V3组成[14],分别为:
| $ \begin{array}{l} {V_1} = \frac{D}{2}\int_{ - \frac{\lambda }{2}}^{\frac{\lambda }{2}} {\int_{ - \frac{a}{2}}^{\frac{a}{2}} {\left\{ {{{\left( {\frac{{{\partial ^2}\omega }}{{\partial {z^2}}} + \frac{{{\partial ^2}\omega }}{{\partial {y^2}}}} \right)}^2} + } \right.} } \\ \;\;\;\;\;\;\;\left. {2\left( {1 - \nu } \right)\left[ {{{\left( {\frac{{{\partial ^2}\omega }}{{\partial z\partial y}}} \right)}^2} - \frac{{{\partial ^2}\omega }}{{\partial {z^2}}}\frac{{{\partial ^2}\omega }}{{\partial {y^2}}}} \right]} \right\}{\rm{d}}z{\rm{d}}y, \end{array} $ | (3) |
| $ {V_2} = \frac{1}{2}\left\{ {{k_\varphi }\int_{ - \frac{\lambda }{2}}^{\frac{\lambda }{2}} {{{\left[ {{{\left( {\frac{{\partial \omega }}{{\partial y}}} \right)}_{y = - \frac{a}{2}}}} \right]}^2}{\rm{d}}z} + {k_\varphi }\int_{ - \frac{\lambda }{2}}^{\frac{\lambda }{2}} {{{\left[ {{{\left( {\frac{{\partial \omega }}{{\partial y}}} \right)}_{y = \frac{a}{2}}}} \right]}^2}{\rm{d}}z} } \right\}, $ | (4) |
| $ {V_3} = \frac{1}{2}\int_{ - \frac{\lambda }{2}}^{\frac{\lambda }{2}} {\int_{ - \frac{a}{2}}^{\frac{a}{2}} {\sigma t{{\left( {\frac{{\partial \omega }}{{\partial z}}} \right)}^2}} } {\rm{d}}z{\rm{d}}y, $ | (5) |
取挠曲函数为[15]
| $ \omega = A\left[ {\frac{{\pi \varepsilon }}{{2{a^2}}}\left( {{y^2} - \frac{{{a^2}}}{4}} \right) + \left( {1 + \frac{\varepsilon }{2}} \right)\cos \left( {\frac{{\pi y}}{a}} \right)} \right]\cos \left( {\frac{{\pi z}}{\lambda }} \right), $ | (6) |
式中ε=akφ/D,D为板的弯曲刚度.
将式 (6) 带入式 (3)~(5) 中,根据能量守恒,即V1+V2=V3,可解得局部屈曲荷载σ为
| $ \sigma = k\frac{{{\pi ^2}E}}{{12\left( {1 - {\nu ^2}} \right)}}{\left( {\frac{t}{a}} \right)^2}, $ | (7) |
其中稳定系数k为
| $ k = \frac{{\left[ {\frac{{{{\left( {\pi a} \right)}^4} + 120{\lambda ^4}}}{{120{\pi ^2}{a^2}{\lambda ^2}}} + \frac{1}{6}} \right]{\varepsilon ^2} + {\eta _1}{{\left( {\frac{{{a^2} + {\lambda ^2}}}{{a\lambda }}} \right)}^2}\left[ {\frac{1}{2}{\eta _1} - \frac{{4\varepsilon }}{{{\pi ^2}}}} \right] + \frac{{2\varepsilon {\lambda ^2}}}{{{{\left( {\pi a} \right)}^2}}}}}{{\frac{{{\pi ^2}{\varepsilon ^2}}}{{120}} - \frac{{4\varepsilon }}{{{\pi ^2}}}{\eta _1} + \frac{1}{2}\eta _1^2}}, $ | (8) |
式中η1=(1+ε/2),ε=akφ/D.
令ək/əλ=0,可解得临界半波长度为
| $ {\lambda _{{\rm{cr}}}} = \sqrt[4]{{\frac{{{a^4}}}{{15}}\frac{{{\varepsilon ^2}\left( {{\pi ^4} + 15{\pi ^2} - 240} \right) + \varepsilon \left( {60{\pi ^2} - 480} \right) + 60{\pi ^2}}}{{{\varepsilon ^2}\left( {{\pi ^2} - 8} \right) + \varepsilon \left( {4{\pi ^2} - 16} \right) + 4{\pi ^2}}}}}. $ | (9) |
转动约束刚度kφ是求解式 (8)、(9) 的关键参数,本节将通过受压板件间的变形协调条件对该参数进行求解.取翼缘分离体和卷边分离体为分析对象,如图 2(b)和图 2(c)所示,并假定:1) 相邻板件的交线保持挺直;2) 相邻板件的交角不变,即:φw=φf1,φf2=φp.式中:φw、φf1分别为腹板、翼缘在腹板-翼缘交线处的转角,如图 1(b)所示,φf2、φp分别为翼缘、卷边在翼缘-卷边交线处的转角.
3.1 翼缘和卷边的挠曲函数由图 2知,翼缘和卷边的挠曲变形受到侧向分布弯矩和轴向受压的共同影响,为便于分析,本文参考Bleich的理论[16]对这种耦合作用进行解耦,即取kφ=rkφ1,其中kφ1是仅考虑侧向分布弯矩影响下的翼缘和卷边对腹板的转动约束刚度kφ1,而r是考虑轴向压力对kφ1不利影响的折减系数.
由文献[17]可知,翼缘和卷边的挠曲变形满足:
| $ \begin{array}{l} {\omega _{\rm{f}}} = \left( {{C_1}\sinh \frac{{\pi y}}{\lambda } + {C_2}\cosh \frac{{\pi y}}{\lambda } + {C_3}y\sinh \frac{{\pi y}}{\lambda } + } \right.\\ \left. {{C_4}y\sinh \frac{{\pi y}}{\lambda }} \right)\sin \left( {\frac{{\pi z}}{\lambda }} \right), \end{array} $ | (10) |
式中C1、C2、C3、C4为常数.
翼缘的边界条件为:
1)y=0,y=b挠度为零
| $ {\omega _{\rm{f}}}\left| {_{y = 0,y = c}} \right. = 0, $ | (11a) |
2)y=0,y=b弯矩平衡
| $ - D{\frac{{{\partial ^2}{\omega _{\rm{f}}}}}{{\partial {y^2}}}_{\left| {_{y = 0}} \right.}} = {M_{{\rm{wf}}}}, - D{\frac{{{\partial ^2}{\omega _{\rm{f}}}}}{{\partial {y^2}}}_{\left| {_{y = b}} \right.}} = {M_{{\rm{pf}}}}, $ | (11b) |
卷边的边界条件为:
1)y=0挠度为零
| $ {w_{\rm{p}}}\left| {_{y = 0}} \right. = 0, $ | (12a) |
2)y=0,y=d弯矩平衡
| $ - D{\frac{{{\partial ^2}{\omega _{\rm{p}}}}}{{\partial {y^2}}}_{\left| {_{y = 0}} \right.}} = {M_{{\rm{fp}}}}, $ | (12b) |
| $ - D\left( {\frac{{{\partial ^2}{\omega _{\rm{p}}}}}{{\partial {y^2}}} + \nu \frac{{{\partial ^2}{\omega _{\rm{p}}}}}{{\partial {x^2}}}} \right)\left| {_{y = d}} \right. = 0, $ | (12c) |
3)y=d剪力为零[14]
| $ {\left[ {\frac{{{\partial ^3}{\omega _{\rm{p}}}}}{{\partial {y^3}}} + \left( {2 - \nu } \right)\frac{{{\partial ^3}{\omega _{\rm{p}}}}}{{{\partial ^2}x\partial y}}} \right]_{\left| {_{y = d}} \right.}} = 0. $ | (12d) |
将式 (11a)~(11b) 和 (12a)~(12d) 分别带入式 (10),可解得翼缘和卷边的挠度函数ωf和ωp,并将其带入翼缘-卷边交角处的变形协调方程əωf/əy|y=b=əωp/əy|y=0, 则有:
| $ \begin{array}{l} {\varphi _{\rm{w}}} = {\varphi _{{\rm{f1}}}} = \\ \;\;\;\;\frac{{{M_{{\rm{wf}}}}\left[ {{\beta _1}\left( {\pi b{\gamma _2} - {\gamma _1}\lambda } \right) + {\beta _2}\left( {\pi b\gamma _1^2 - \pi b\gamma _2^2 + {\gamma _1}{\gamma _2}\lambda } \right)} \right]}}{{\pi D\gamma _1^2{\beta _2}}}, \end{array} $ |
式中β1、β2为γ1~γ4的函数.
| $ \begin{array}{l} {\gamma _1}{\rm{ = }}\sinh \left( {\frac{{\pi b}}{\lambda }} \right),{\gamma _2}{\rm{ = }}\cosh \left( {\frac{{\pi d}}{\lambda }} \right),\\ {\gamma _3}{\rm{ = }}\sinh \left( {\frac{{\pi d}}{\lambda }} \right),{\gamma _4}{\rm{ = }}\cosh \left( {\frac{{\pi d}}{\lambda }} \right). \end{array} $ |
由力的平衡条件可知Mwf=Mfw、kφ1=Mfw/φw,并可解得kφ1的精确解析解为
| $ {k_{\varphi 1}} = \frac{{2\gamma _1^2{\beta _2}D\pi }}{{{\beta _2}\left[ {\left( {{\gamma _1}{\gamma _2}\lambda } \right. + b\pi \left( {\gamma _1^2 - \gamma _2^2} \right)} \right] + {\beta _1}\left( {\pi b{\gamma _2} - \lambda {\gamma _1}} \right)}}. $ | (13) |
式 (13) 的解过于复杂,图 4给出了式中无量纲参数kφλ/2πD、b/λ和d/λ的函数关系图像.

|
图 4 无量纲参数kφλ/2πD、b/λ和d/λ的比较 Figure 4 Comparison of non-dimensional parameters kφλ/2πD、b/λ and d/λ |
由图 4可知,参数d/λ的变化相对于b/λ,对kφλ/2πD的影响较小,即在长为λ的柱段中,卷边宽度d的变化相对于翼缘宽度b,对约束刚度kφ的影响较小.因此,为了增加本文解析解的适用性,可略微保守的忽略卷边与翼缘间的转动约束,即取
| $ {k_{\varphi 1}} = \frac{{2\gamma _1^2D\pi }}{{{\gamma _1}{\gamma _2}\lambda + b\pi \left( {\gamma _1^2 - \gamma _2^2} \right)}}. $ | (14) |
折减系数r的大小,取决于腹板分离体和翼缘分离体 (见图 2) 发生屈曲的趋势,当此二者发生屈曲的趋势较为接近时,即σcr, w≈σcr, f (见式 (1)),此时轴向压力对约束刚度kφ1的削弱较强,折减系数r趋于0,当此二者发生屈曲的趋势差异较大时,即σcr, w远大于σcr, f,此时轴向压力对约束刚度kφ1的削弱较弱,折减系数r趋于1.因此,可取折减系数r为[16]
| $ r = 1 - {b^2}/{a^2}, $ |
综上所述,本文采用平衡法推导了侧向弯矩作用下的kφ精确解析解,即式 (13).考虑卷边宽度变化对转动约束刚度kφ影响较小,给出了kφ的简化解析解,即式 (14).考虑轴压应力的不利影响,得到了计算临界荷载所需的kφ解析解:
| $ {k_\varphi } = \frac{{2\gamma _1^2D\pi }}{{{\gamma _1}{\gamma _2}\lambda + b\pi \left( {\gamma _1^2 - \gamma _2^2} \right)}}\left( {1 - \frac{{{b^2}}}{{{a^2}}}} \right). $ | (15) |
式 (15) 为隐含λ的超越方程,联立式 (15) 和式 (9) 求解λ时,只能采用数值方法.为简化计算,在计算kφ时可略微偏安全的取λ=a,将其代入式 (7)~(9),即可求解试件的屈曲临界应力.
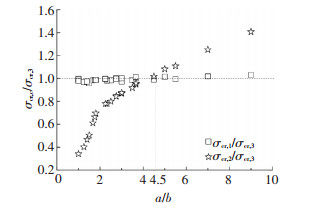
4 算例分析 4.1 弹性局部屈曲的分析设计了24组不同截面尺寸的冷弯薄壁C形截面,见表 1.分别按本文解析解、中国规范 (取腹板k=4)[13]和有限条软件CUFSM[18]对表 1试件的局部屈曲临界荷载进行计算,结果见图 5和表 2.
| 表 1 冷弯C形钢的截面尺寸 Table 1 Dimensions of lipped channel sectionsmm |
|
注:σcr, 1、σcr, 2、σcr, 3分别为按本文公式、中国规范和CUFSM计算出的局部屈曲荷载值 图 5 局部屈曲荷载计算值与CUFSM分析结果比较 Figure 5 Local buckling comparison of theoretic values and CUFSM results |
| 表 2 局部屈曲承载力比较 Table 2 Comparisons of the local buckling strength |
由图 5可知,本文解析解与CUFSM分析结果较为接近,而中国规范与CUFSM分析结果存在系统误差,当截面高宽比小于4.5时,中国规范偏于保守,截面高宽比大于4.5时,偏于不安全.
4.2 轴压构件的局部屈曲承载力分析 4.2.1 本文推荐方法前述提出的解析解 (式 (7)~(9)) 给出了薄壁受压C形截面的局部屈曲荷载,但精确计算构件的承载力时还需计及屈曲后强度和材料参数的影响.本文将所提出的解析解引入直接强度法[3]的局部屈曲强度曲线中,得到了可以考虑板组效应影响的局部屈曲承载力计算公式:
当λL≤0.776时, PnL=Pne;
当λL>0.776时
式中:PnL为局部屈曲承载力,λL=
为验证本文方法的正确性,收集了23根冷弯薄壁C形受压短柱试件[19],短柱试验的目的是考察构件的局部屈曲承载力,其试件的截面尺寸和材料参数详见文献[19],表 2分别给出了按中国规范计算方法 (考虑板组效应) 和本文建议方法计算的构件承载力的对比结果,其中PE、Pu, C和Pu, D分别为试件的承载力试验值、中国规范计算的承载力和本文方法计算的承载力.
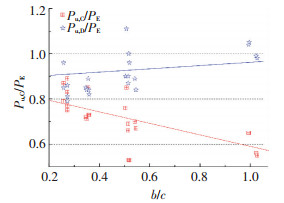
为了方便比较,图 6给出了算例中Pu, C/PE和Pu, D/PE随截面宽高比b/c变化的曲线.Pu, D/PE随b/c变化的趋势比Pu, C/PE更加平缓,说明本文方法更好反映出试件承载力与截面宽高比之间的关系.表 2和图 6的对比分析表明,本文建议的局部屈曲承载力计算方法合理有效,具有较好的适用性.
|
图 6 局部屈曲承载力计算值与试验结果比较 Figure 6 Local buckling strength comparison of theoretic values and experiment results |
1) 基于能量法和变形协调条件推导出的冷弯薄壁C形截面的腹板局部屈曲临界荷载解析解合理可靠.
2) 按中国规范规定的稳定系数 (取腹板k=4) 计算的冷弯薄壁C形截面的腹板弹性局部屈曲临界荷载存在系统误差,当截面高宽比小于4.5时,中国规范偏于保守,截面高宽比大于4.5时,偏于不安全.
3) 按中国规范计算的冷弯薄壁受压短柱的局部屈曲承载力较为保守,并且随着截面宽高比的增大,这种趋势不断增大.
| [1] |
陈绍蕃.
钢结构稳定设计指南[M]. 第2版. 北京: 中国建筑工业出版社, 2004: 204-215.
CHEN Shaofan. Guide to stability design of steel structure[M]. 2nd ed. Beijing: China Architecture & Building Press, 2004: 204-215. |
| [2] | Australian/New Zealand standard cold-formed steel structures: AS/NZS 4600:2005[S]. Sydney: Standards Australia and Standards New Zealand, 2005. |
| [3] | North American cold-formed steel specification: AISI-S100-2007[S]. Washington: American Iron and Steel Institute, 2007. |
| [4] |
陈绍蕃. 卷边槽钢的局部相关屈曲和畸变屈曲[J].
建筑结构学报, 2002, 23(1): 27-32.
CHEN Shaofan. Local interactive bucking and distortional buckling of lipped channels[J]. Journal of Building Structures, 2002, 23(1): 27-32. |
| [5] | SCHAFER B W. Review: the direct strength method of cold-formed steel member design[J]. Journal of Constructional Steel Research, 2008, 64(7): 766-778. |
| [6] | RHODES J, HARVEY J M. Plain channel section struts in compression and bending beyond the local buckling load[J]. International Journal of Mechanical Sciences, 1976, 18(9/10): 511-519. |
| [7] |
周绪红. 开口薄壁型钢压弯构件中板件屈曲后性能与板组屈曲后相关作用的研究[D]. 湖南: 湖南大学, 1992.
ZHOU Xuhong. The research on the behavior of plate elements and plate-assemblies of open thin-walled beam-columns in post-buckling range[D]. Hunan: Hunan University, 1992. |
| [8] |
周绪红, 莫涛, 周期石, 等. 边缘加劲板件有效宽厚比设计方法中的板组效应研究[J].
建筑结构学报, 2002, 23(3): 37-43.
ZHOU Xuhong, MO Tao, ZHOU Qishi, et al. Study on the plate assembly effects on edge stiffened plate elements in design approach of effective width to thickness ratio[J]. Journal of Building Structures, 2002, 23(3): 37-43. |
| [9] | SCHAFER B W, PEKÖZ T. Direct strength prediction of cold-formed steel members using numerical elastic buckling solutions[R]. Proceedings of the fourteenth international specialty conference on cold-formed steel structures. St. Louis, MO:[s.n.], 1998: 69-76. |
| [10] | LAU S C W, HANCOCK G J. Distortional Buckling Formulas for Channel Columns[J]. Journal of Structural Engineering, 1987, 113(5): 1063-1078. DOI: 10.1061/(ASCE)0733-9445(1987)113:5(1063) |
| [11] | SEIF M, SCHAFER B W. Local buckling of structural steel shapes[J]. Journal of Constructional Steel Research, 2010, 66(10): 1232-1247. DOI: 10.1016/j.jcsr.2010.03.015 |
| [12] |
王春刚, 张耀春. 冷弯薄壁斜卷边槽钢轴压构件的稳定性分析[J].
哈尔滨工业大学学报, 2009, 41(12): 14-19.
WANG C G, ZHANG Y C. Stability behavior of channels with inclined simple edge stiffeners under axial compression[J]. Journal of Harbin institute of technology, 2009, 41(12): 14-19. DOI: 10.3321/j.issn:0367-6234.2009.12.003 |
| [13] |
冷弯薄壁型钢结构技术规范: GB 50018-2002[S]. 北京: 中国计划出版社, 2002.
Technical code of cold-formed thin-wall steel structures: GB 50018-2002[S]. Beijing: China Planning Press, 2002. |
| [14] | TIMOSHENKO S. Theory of elastic stability[M]. New York, NY: McGraw-Hill, 1961. |
| [15] | LUNDQUIST E E. Critical compressive stress for flat rectangular plates supported along all edges and elastically restrained against rotation along the unloaded edges[J]. Technical Report Archive & Image Library, 1942. |
| [16] | BLEICH F. Buckling strength of metal structures[M]. New York: McGraw-Hill, 1952. |
| [17] | TIMOSHENKO S. Theory of plates and shell[M]. 2nd ed. New York: McGraw-Hil, 1959. |
| [18] | LI Z, SCHAFER B W. Application of the finite strip method in cold-formed steel member design[J]. Journal of Constructional Steel Research, 2010, 66(8/9): 971-980. |
| [19] | MULLIGAN G P. The influence of local buckling on the structural behavior of singly-symmetric cold-formed steel columns[D]. Ithaca: Cornell University, 1983. http://ascelibrary.org/doi/10.1061/%28ASCE%290733-9445%281984%29110%3A11%282635%29 |
 2017, Vol. 49
2017, Vol. 49


