2. 岩土及地下工程教育部重点实验室 (同济大学),上海 200092;
3. 青岛理工大学 土木工程学院,山东 青岛 266520
2. Key Laboratory of Geotechnical and Underground Engineering (Tongji University), Ministry of Education, Shanghai 200092, China;
3. Department of Civil Engineering, Qingdao University of Technology, Qingdao 266520, Shandong, China
随着岩体工程规模的扩大,岩体的流变性质引起了国内外众多学者的关注,目前对于岩体流变的研究主要集中在岩石的蠕变性质上,对应力松弛和长期强度的研究还相对较少,特别是对长期强度的研究,还没有给予足够的重视,而相关研究表明,岩体在长期荷载作用下的强度低于峰值强度,并且在实际工程中,大多数的岩体失稳表现出了与时间因素相关的强度特性[1-3].因此,长期强度在工程中具有重要的应用价值.
岩石的长期强度是时效强度的一种,是岩石在工程运行时间内,不发生破坏的最大可能作用力[4].国内外学者通过对岩石的长期试验,得到了一些长期强度的经验数值及确定方法,Schmidtke等[5]通过岩石静态疲劳试验得出了引起花岗岩试件逐步破坏的最小载荷是单轴抗压强度的60%;Szczepanik等[6]得出花岗岩在长期加载条件下,当荷载为常规单轴压缩试验峰值强度的70%~80%时,试样开始出现扩容现象,而这个荷载值可作为长期强度; Damjanac等[7]通过Lac du Bonnet花岗岩强度与破坏时间的关系以及对裂隙的数值分析试验证实了岩石在荷载作用下开始起裂的应力阈值可作为长期强度,且这个值为瞬时强度的40%~60%;崔希海等[8]提出岩石的长期强度应根据岩石进入横向稳定蠕变的阈值应力来确定,这样确定的长期强度要比根据岩石进入轴向稳定蠕变的阈值应力所确定的值小19%~35%.在研究过程中也形成了一些确定长期强度的方法,主要有等时曲线法、过渡蠕变法、流动曲线法、横向蠕变阙值法、蠕变曲线第一拐点法[9-12].其中等时曲线法和过渡蠕变法应用较广泛,但是等时曲线的拐点变化规律具有多样性,规律性较差,求解拐点比较困难;而过渡蠕变法得出的长期强度是一个范围值,该范围值的大小与蠕变试验的应力分级有关,因此具有一定的局限性.通过以上的研究成果可以看出,由于长期强度的确定方法不同,其数值也各有差异,从而造成了对长期强度研究的欠缺,所以还需继续寻找一种试验时间短,实用可靠的方法去解决岩石长期强度的求解问题.
本文在蠕变试验曲线的基础上,绘制了等应变速率曲线,利用等应变速率曲线中黏弹性和黏塑性转折点的力学意义和Goodman[13]提出的极限应变规律,分别推算等应变速率曲线的拐点和极限应变轨迹,提出了两种基于等应变速率曲线的长期强度求解方法——等应变速率曲线拐点法和极限应变法,并且通过单轴和三轴蠕变试验验证了新方法的可行性.
1 室内试验 1.1 试验样品试样为取自锦屏二级水电站的绿片岩,取样位置埋深1 600 m, 自重应力42 MPa,虽然绿片岩为硬质岩,但已有成果表明该岩石存在着较为明显的流变特性[14].取样过程中尽量保证各岩石样品的层理方向一致,且严格按照《工程岩体试验方法标准》[15]的要求进行制样,试验样品见图 1,试验加载方向均垂直于岩石层理方向.

|
图 1 试验样品 Figure 1 Samples |
单轴常规及分级加载蠕变试验采用CSS-1950型双轴压缩流变试验机,该试验机采用伺服控制,最大轴向出力为500 kN,测力精度在±1%以内,变形测量精度为1 μm;三轴常规及蠕变试验在TLW-2000型岩石三轴流变试验机上进行,试验机的最大轴向出力为2 000 kN,最大围压为50 MPa,测力精度在±1%以内,变形测量精度在±0.5%以内,室内温度始终控制在 (20±1) ℃.
1.2.2 试验方案本次试验分为常规试验和蠕变试验,具体试验种类、数量以及最后的破坏强度见表 1.其中常规试验的破坏强度作为蠕变试验的分级依据.
| 表 1 试验概况表 Table 1 Test information |
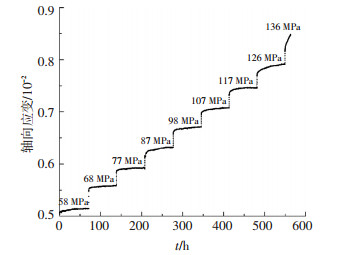
常规单轴和三轴试验根据《工程岩体试验方法标准》[15]的要求进行;蠕变试验采取分级加载的方式,即首先通过油液压系统给岩样施加围压至预定值,直至该围压下变形稳定 (单轴蠕变试验此步略去);然后按照0.2 mm/min的加载速率,分级增加轴压至预定值,加载到每一级预定值后,保持轴压恒定,记录试样轴向以及侧向应变与时间的关系.由于长期强度预先无法估计,按照常规试验峰值强度的50%左右开始,分级加载,每级加载时间为72 h直至该试样破坏, 蠕变试验全过程曲线见图 2~4.
|
图 2 单轴蠕变全过程曲线 Figure 2 Complete creep curve of uniaxial mutistage creep tests |
|
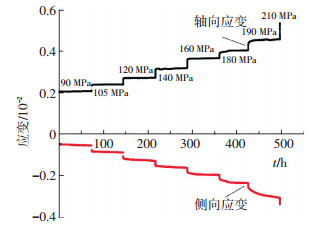
图 3 三轴蠕变全过程曲线 (围压10 MPa) Figure 3 Complete creep curve (confining pressure: 10 MPa) |
|
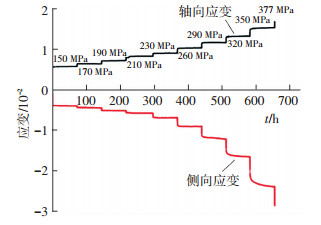
图 4 三轴蠕变全过程曲线 (围压40 MPa) Figure 4 Complete creep curve (confining pressure: 40 MPa) |
如图 2、3、4所示,在分级加载蠕变试验过程中,轴向瞬时变形产生的应变量在第一级荷载时较大,之后各级瞬时变形产生的应变量变化趋于平稳,蠕变变形产生的轴向应变量随轴向应力的升高而增加,但在某个应力级别上轴向和横向应变均会显著增加;以40 MPa三轴蠕变试验为例,如表 2所示在第6级 (260 MPa) 以后的轴向应变量和侧向应变量均较前几级有显著的增加.
| 表 2 蠕变试验应变量及平均蠕变速率统计表 Table 2 Creep stain and average creep strain rate of multistage creep tests with confining pressure |
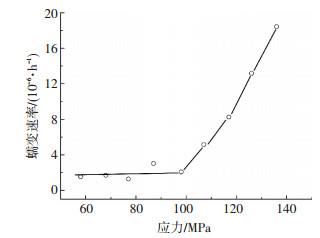
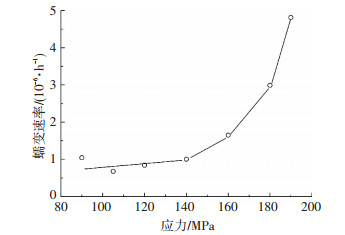
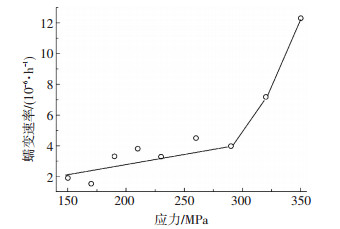
为了对绿片岩的长期强度范围值进行大致的分析,笔者对每级荷载下蠕变阶段的平均应变速率进行了计算分析,见图 5~7,三种应力状态下试验的蠕变平均速率分别在应力为98、140、290 MPa以后发生了显著的变化,可以认为,黏塑性应变速率和黏塑性变形的加入使得高应力下的应变速率以及变形远大于低应力,而黏弹性到黏塑性转折点的应力水平,即黏塑性应变速率大于零的最小应力水平,可以定义为长期强度[16].因此可以估算单轴以及10 MPa和40 MPa围压下岩石的长期强度范围为:98~107 MPa、140~160 MPa,290~320 MPa.
|
图 5 轴向平均蠕变速率与应力关系 (单轴) Figure 5 Relationship between average creep rate and stress of uniaxial multi-stage creep tests |
|
图 6 轴向平均蠕变速率与应力关系 (围压10 MPa) Figure 6 Relationship between average creep rate and stress (confining pressure: 10 MPa) |
|
图 7 轴向平均蠕变速率与应力关系 (围压40 MPa) Figure 7 Relationship between average creep rate and stress (confining pressure: 40 MPa) |
在高应力下一条完整的蠕变曲线包括3个阶段:初始蠕变阶段、稳态蠕变阶段、加速蠕变阶段[13].任何条件下岩石的蠕变均会经历第一阶段,只有应力大于长期强度时才会存在应变速率不为零的稳态蠕变阶段和加速蠕变阶段,否则当应变速率降至零,蠕变停止.因此对于典型的蠕变曲线,在小于长期强度的应力水平或者加载时间较短的情况下,应变速率是逐渐减小最后趋向于0的,因此在应力为σ(σ加载时间较短或小于长期强度) 的蠕变曲线中,每个蠕变的时间点都对应着唯一的应变ε和速率v.可以利用 (σ,ε,v) 三者之间一一对应的关系,先在蠕变速率变化曲线中分别取不同荷载下速率相同的时间点,然后在蠕变曲线上求得该时间点的变形,利用取得的 (σ,ε,v) 数据,将相等速率的 (σ,ε) 在应力-应变坐标系中绘制曲线,即可得到等应变速率曲线.
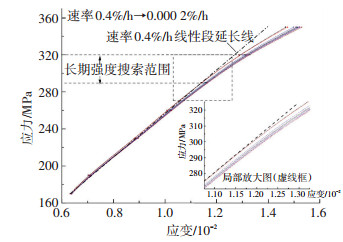
根据上述方法,以40 MPa蠕变试验为例:取应变速率为0.4%/h、0.2%/h、0.1%/h、0.05%/h、0.005%/h、0.002%/h、0.001%/h、0.000 5%/h、0.000 4%/h、0.000 2%/h (h为小时) 等十组应变速率每级荷载下所对应的时间t, 根据每级应力下该速度所对应的时间,在蠕变全过程曲线 (图 4) 上求得所对应的应变值,在应力-应变坐标系中绘制曲线,曲线上各点的应变速率相等,即为蠕变等应变速率曲线,见图 8.
|
图 8 等应变速率曲线 (40 MPa) Figure 8 Isostrain-rate creep curve (40 MPa) |
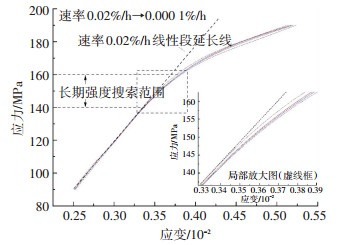
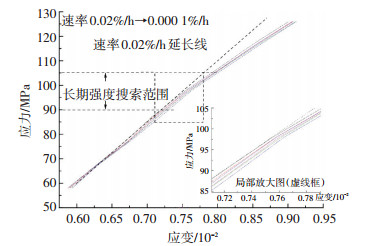
图 9、10为单轴及10 MPa围压下的等应变速率曲线,从图中可以看出,曲线在某个应力水平下发生了明显的转折,特别是10 MPa围压下的等应变速率曲线更为明显,从图中可以发现,这个转折点的应力值在利用平均蠕变速率判断的长期强度范围之内.
|
图 9 等应变速率曲线 (10 MPa) Figure 9 Isostrain-rate creep curve (10 MPa) |
|
图 10 等应变速率曲线 (单轴) Figure 10 Isostrain-rate creep curve (uniaxial) |
崔旋等[16]在其文章中,将长期强度定义为黏塑性变形速率为0时的最大应力水平,即长期强度以下仅存在瞬时变形和黏弹性变形,而长期强度以上则存在瞬时变形、黏弹性变形和黏塑性变形,高应力下由于黏塑性变形的加入,其应力应变曲线表现为由近似线性到非线性的转变[1, 17],并且黏塑性变形是造成岩石大变形以至于破坏的主要原因[18].
等应变速率曲线的力学意义是不同加载速率条件下岩石应力-应变关系的反映,见图 8~10,其曲线形态在一定的应力水平时会发生变化,即每条等应变速率曲线都由近似线性段 (黏弹性段) 和非线性段 (黏塑性段) 组成,并且具有明显的转折点,而该转折点标志着岩石变形由黏弹性到黏塑性的转变,应力超过这个点以后,岩石内部开始发生破坏,整个岩石发生破坏仅是“时间”问题,因此这个转折点可以认为是长期强度.
2.2.2 等应变速率曲线拐点法求解过程以40 MPa围压下的三轴蠕变试验为例:从图 8可见,在290 MPa以下,曲线基本呈线性关系,在290 MPa以上曲线开始发生转折,即呈现非线性关系,并且随着应力水平的升高,这种转折越来越明显.因此根据前述等速率曲线拐点法的求解原理和过程,只需求得这条曲线的转折点 (拐点) 就可以得到长期强度.
将等应变速率曲线分为两段即线性段和非线性段,利用Levenberg-Marquardt法,对曲线分段拟合,搜索可能的拐点,最后以非线性段在转折点的斜率与直线段斜率差值最小做为判据,求解拐点,其应力值即为长期强度.表 3中列出了拐点的求解成果,结果显示出了良好的规律性,其应力水平均为300 MPa左右.根据以上分析,该数值可作为40 MPa围压下绿片岩的长期强度.
| 表 3 拐点求解成果 Table 3 Results of inflection points |
根据上述方法,3种不同围压下岩石的长期强度为:98.5、143、300 MPa.因此,3种不同围压下的长期强度分别为破坏强度的66.9%、68.0%、79.6%.由上述成果可知,围压是影响长期强度的重要因素之一,随着围压的升高,长期强度及长期强度与瞬时破坏强度的比值均随之升高.
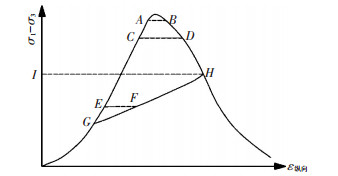
2.3 极限应变法求解长期强度 2.3.1 极限应变规律Goodman[13]提出蠕变与瞬时加载产生的应力-应变全过程曲线存在以下关系 (图 11):长期强度以上的岩石蠕变破坏变形值,与瞬时全应力应变曲线峰后同一应力下的应变量十分相似,从A点开始的蠕变试验经过较短的时间会在瞬时全应力应变曲线峰后的B点破坏,在C点开始的蠕变试验要经过较长的时间,才会在D点破坏,在临界应力水平I点以下的E点开始的蠕变试验则经过很长时间才会逼近F点,而且不会引起破坏.轨迹线GH,则是岩石试样在临界应力以下的各级荷载最终变形 (如F点) 连成的一条轨迹线,此时该轨迹线上所有点的应变速率为0.这条曲线Bérest也做了相关的研究,称作极限应变轨迹[19].
如图 11所示,极限应变轨迹与全应力应变曲线交于H点,此荷载下经过长时间变形,能够与全应力应变曲线峰后段相交,这时蠕变达到破坏所需要的时间最长,而需要的应力水平最低,所对应的破坏变形量最大,因此H点所对应的应力水平即为长期荷载下岩石不发生破坏的临界值,此应力值可作为长期强度.这个规律已在文献[20-21]的试验中得到了证实.
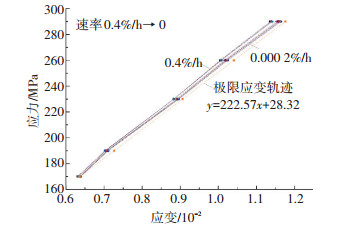
2.3.2 极限应变法的求解过程根据上述原理,H(图 12) 点的应力水平即为长期强度,而其应变量可认为是长期强度作用下的破坏应变量,因此若能绘制极限应变轨迹线,即蠕变试验低应力下每级荷载的最终变形量 (或应变速率为0) 点的连线,与全应力-应变曲线相结合,便可求出长期强度和预估变形稳定时间.
|
图 12 等应变速率曲线 (低应力) Figure 12 Isostrain-rate curve (lower stress) |
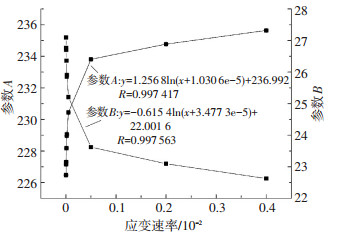
以40 MPa围压的三轴蠕变试验为例,见图 12,在小于290 MPa的应力水平时,等应变速率曲线表现出了较大的线性相关性,均可用σ=Aε+B描述曲线的形式,且拟合后的R值大于0.999 7,因此可找出上述方程中参数A、B与应变速率的关系,最终推算应变速率为0的曲线方程.应变速率与参数A和B的关系见图 13:根据参数A、B与速率的变化规律可推算应变速率为0的曲线的拟合方程参数Av=0=222.57,Bv=0=28.32.该方程为极限应变轨迹方程.
|
图 13 参数A、B与应变速率的关系 Figure 13 Relationship between parameter A and B with strain rate |
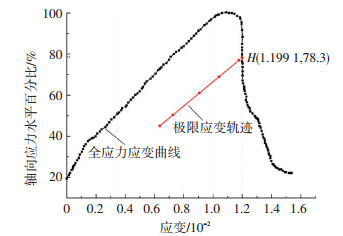
“v=0”时曲线上各点对应的应变为极限应变,即此时由于应变速率为0,各点应变量不会增加,因此,该曲线为极限应变轨迹,根据极限应变法的原理,可通过三轴压缩试验得到的全应力应变曲线与极限应变轨迹的交点近似得到长期强度,为了避免由于试样个体差异造成的破坏强度不相同,对应力进行了归一化处理,图中纵轴为测得应力值与瞬时破坏强度的比值,见图 14,该岩石的长期强度为峰值强度的78.3%,其值为295 MPa.
|
图 14 极限应变法求解长期强度 Figure 14 Long-term strength determined by limit strain method |
根据上述方法,同样可得到10 MPa围压下绿片岩的长期强度为峰值强度的66.2%,其值为139.2 MPa.由于常规单轴压缩试验未得到理想的全应力应变曲线,因而不能用该方法得到长期强度.但是根据计算结果仍然可知:随着围压的增大,长期强度与瞬时破坏强度的比值增大.
3 岩体变形稳定时间的计算极限应变法的求解过程可计算出试验样品在长期强度以下任一应力的极限应变值,由于蠕变曲线是时间t与应变ε的关系曲线,因此可根据蠕变曲线和极限应变值推算出变形稳定时间,例如40 MPa围压下应力为260 MPa时,极限应变轨迹 (图 12) 显示极限应变为1.04%,根据蠕变全过程曲线 (图 4) 的整体趋势可预测260 MPa的应力下,蠕变变形稳定时间为2 741.23 h.
4 结论1) 两者求解成果相差不大,且符合长期强度的经验数值,数据相对传统的求解方法较为客观可靠.
2) 等应变速率曲线拐点法,依据全应力应变曲线中拐点是黏弹性到黏塑性的转折点这一特征求解长期强度,虽然需要较多级的蠕变曲线,才能准确的求得长期强度,但是相对于传统的求解方法 (如等时曲线法),等应变速率曲线的力学意义更为明确,且试验可操作性强.
3) 极限应变法将Goodman提出的极限应变规律引入到长期强度的求解中,可减少求解长期强度的试验时间及试验数量,可实现对长期强度的快速求解.
4) 围压是影响长期强度的重要因素之一,具体表现为随着围压的升高,长期强度与峰值强度的比值升高.
| [1] | FABRE G, PELLET F. Creep and time-dependent damage in argillaceous rocks[J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(6): 950-960. DOI: 10.1016/j.ijrmms.2006.02.004 |
| [2] | MALAN D F. Time-dependent behaviour of deep level tabular excavations in hard rock[J]. Rock Mechanics and Rock Engineering, 1999, 32(2): 123-155. DOI: 10.1007/s006030050028 |
| [3] |
田光辉, 沈明荣, 周文锋, 等. 分级加载条件下的锯齿状结构面剪切松弛特性[J].
哈尔滨工业大学学报, 2016, 48(12): 108-113.
TIAN Guanghui, SHEN Mingrong, ZHOU Wenfeng, et al. Shear relaxation characteristic of serrate structure surface under stepwise loading[J]. Journal of Harbin institute of technology, 2016, 48(12): 108-113. DOI: 10.11918/j.issn.0367-6234.2016.12.015 |
| [4] |
刘雄.
岩石流变学概论[M]. 北京: 地质出版社, 1994: 194-207.
LIU Xiong. Rheology of rocks[M]. Beijing: Geological Publishing House, 1994: 194-207. |
| [5] | SCHMIDTKE R H, LAJTAI E Z. The long-term strength of Lac du Bonnet granite[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1985, 6(22): 461-465. |
| [6] | SZCZEPANIK Z, MOLNE D, KOSTAKIS K, et al. Longterm laboratory strength tests in hard rock[C]//ISRM2003-Technology Road map for Rock Mechanics. Johannesburg: South African Institute of Mining and Metallurgy, 2003: 1179-1184. |
| [7] | DAMJANAC B, FAIRHURST C. Evidence for a long-term strength threshold in crystalline rock[J]. Rock Mechanics and Rock Engineering, 2010, 43(5): 513-531. DOI: 10.1007/s00603-010-0090-9 |
| [8] |
崔希海, 付志亮. 岩石流变特性及长期强度的试验研究[J].
岩石力学与工程学报, 2006, 25(5): 1021-1024.
CUI Xihai, FU Zhiliang. Experimental study on rheology properties and long-term strength of rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(5): 1021-1024. |
| [9] |
刘晶辉, 王山长, 杨洪海. 软弱夹层流变试验长期强度确定方法[J].
勘察科学技术, 1996, 5: 3-7.
LIU Jinghui, WANG Shanchang, YANG Honghai. Method to determine the rheological test long term strength for soft interclations[J]. Site Investigation Science and Technology, 1996, 5: 3-7. |
| [10] |
沈明荣, 谌洪菊, 张清照. 基于蠕变试验的结构面长期强度确定方法[J].
岩石力学与工程学报, 2012, 31(1): 1-7.
SHEN Mingrong, CHEN Hongju, ZHANG Qingzhao. Method for determining long-term strength of discontinuity using shear creep test[J]. Rock Mechanics and Engineering, 2012, 31(1): 1-7. |
| [11] |
沈明荣, 谌洪菊. 红砂岩长期强度特性的试验研究[J].
岩土力学, 2011, 32(11): 3301-3305.
SHEN Mingrong, CHEN Hongju. Testing study of long-term strength characteristics of red sandstone[J]. Rock and Soil Mechanic, 2011, 32(11): 3301-3305. DOI: 10.3969/j.issn.1000-7598.2011.11.017 |
| [12] |
刘传孝, 贺加栋, 张美政, 等. 深部坚硬细砂岩长期强度试验[J].
采矿与安全工程学报, 2010, 27(4): 581-584.
LIU Chuanxiao, HE Jiadong, ZHANG Meizheng, et al. Long-term strength test and application of hard fine sandstone in deep site[J]. Journal of Mining and Safety Engineering, 2010, 27(4): 581-584. |
| [13] | GOODMAN R E. Introduction to rock mechanic[M]. America: Wiley, 1989. |
| [14] |
石振明, 张力. 锦屏绿片岩分级加载流变试验研究[J].
同济大学学报 (自然科学版), 2011, 39(3): 320-326.
SHI Zhenming, ZHANG Li. Study on rheological test of Jinping greenschist under step load[J]. Journal of Tongji University (Natural Science), 2011, 39(3): 320-326. |
| [15] |
工程岩体试验方法标准: GB/T 50266-2013[S]. 北京: 中国计划出版社, 2013.
Standard for tests method of engineering rock mass: GB/T 50266-2013[S]. Beijing: China Planning Press, 2013. |
| [16] |
崔旋, 佘成学. 推断岩石长期强度的黏塑性应变率法研究[J].
岩石力学与工程学报, 2011, 30(S2): 3899-3904.
CUI Xuan, SHE Chengxue. Study of viscoplastic strain rate method to quickly determine long-Term strength of rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(S2): 3899-3904. |
| [17] | GASC-BARBIER M, CHANCHOLE S, BÉREST P. Creep behavior of Bure clayey rock[J]. Applied Clay Science, 2004, 26(1): 449-458. |
| [18] |
孙钧. 岩石流变力学及其工程应用研究的若干进展[J].
岩石力学与工程学报, 2007, 26(6): 1081-1106.
SUN Jun. Rock Rheological Mechanics and its Advance in Engineering Applications[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(6): 1081-1106. |
| [19] | BÉREST P, BERGUS J, DUC N M. Comportement des roches au coursdela rupture: application á l'interprétation d'essaissur des tubesépais[J]. Rev franc-aise Géotech, 1979, 9: 5-12. |
| [20] |
葛修润, 卢应发. 循环荷载作用下岩石疲劳破坏和不可逆变形问题的探讨[J].
岩土工程学报, 1992, 14(3): 56-60.
GE Xiurun, LU Yingfa. Study on fatigue damage and irreversible deformation law rock under, cyclic load[J]. Chinese Journal of Geotechnical Engineering, 1992, 14(3): 56-60. |
| [21] |
肖建清, 丁德馨, 徐根, 等. 常幅循环荷载下岩石的变形特性[J].
中南大学学报 (自然科学版), 2010, 41(2): 685-691.
XIAO Jianqing, DING Dexin, XU Gen, et al. Deformation characteristics of rock under constant amplitude cyclic loading[J]. Journal of Central South University (Natural Science Edition), 2010, 41(2): 685-691. |
 2017, Vol. 49
2017, Vol. 49